rdrobustを用いたRDDの実行
回帰不連続デザイン(RDD)は、連続変数のあるカットオフ値の前後で処置と統制が決定されるケースにおいて、カットオフ値近傍のデータを用いて平均処置効果を算出することができる方法です。処置と統制をランダムに割り振ることができないような状況でも効果検証に挑戦できる手法、いわゆる準自然実験手法の一つです。
ノンパラメトリックなRDDの肝の一つは、近傍を選択するバンド幅の選び方です。一般的に、バンド幅を大きくするとより多くのサンプルを推定対象とすることができますが、推定量のバイアスが大きくなるとされています。これはカットオフから離れた値も推定に用いるために発生します。一方でバンド幅を小さくすると推定量のバイアスは小さくなりますが、バンド幅に含まれるサンプルサイズは小さくなるために推定量の分散は大きくなるとされています。このBias-Varianceのトレードオフに向き合ってバンド幅を選択する必要があります。従来のRDDでは、このバランスを取りながらバンド幅を選択し、適切なカーネル関数を用いてカットオフの前後で重み付き多項式回帰を行って推定量を計算します。
この従来の手法について、バンド幅が「大きくなりすぎる」ことで推定量に無視できないバイアスが生じると指摘するのが、 Calonico, Cattaneo, and Titiunik (2014) です。この論文では、よりロバストな信頼区間の推定を可能とするノンパラメトリックモデルを提案し、StataやRでのパッケージも提供されています。
今回はこの論文の問題意識と提案されている手法を簡単にレビューし、それを用いて人工データを用いたRコードを紹介しようと思います。
もともと川口、澤田(2024)「因果推論の計量経済学」では多くのページを割いてこのトピックが説明されていた一方で、zenn, qiita等の記事におけるRDDはRでの実装がなかったり、カーネル推定量が説明されているのを散見したため、本記事を執筆しました。
RDDの仮定と推定方法
RDDは以下の仮定のもとに成立します。なお、処置をダミー変数で表し、処置が行われない場合の潜在結果を
①
②
③
事前決定された共変量
特に、①が成り立つことでカットオフ近傍の無作為化が成り立ち、近傍において
が成立します。右辺がカットオフ値をとる人のATEを表していることから、カットオフ近傍の期待値の差分をとることで識別できることが分かります。
川口、澤田(2024)では、従来のパラメトリック推定の説明と問題点が説明され、それに続く形でノンパラなLocal Linear Regressionが紹介されています。これらの説明は川口、澤田(2024)を参照ください。
Calonico, Cattaneo, and Titiunik (2014)の推定方法
従来のRDDではこのバンド幅の選択において、カーネル推定量(Nadaraya-Watson推定量)が用いられ、このときの評価指標としてMSEが一般的に使われました。しかしこのようなカーネル推定量を用いることは「まずない」(川口、澤田(2024))ようです。その理由として推定量にバイアスが生じるメカニズムが紹介されている。本書では、その解決策としてLocal Linear Estimationを挙げており、端点におけるバイアスの存在が漸近MSEの観点でより考慮される(除去できる)と説明されている。
以下の議論で用いるRパッケージの"rdrobust"を提案したCalonico et al.(2014)は、局所二次回帰(Local Quadratic Regression)によるバイアス推定値を用いてRDD推定量のバイアスを補正し、信頼区間を補正することを提案しています。細かな議論に関しては豊富に説明されている(川口、澤田(2024))P163~P174をご覧ください。
人工データを用いたクエリ実行
今回はある会員サービスを想定し、キャンペーン施策の効果検証を行うケースを想定します。
あるECサイトでは、前月の当該サイトでの購入金額が2500円以上であるユーザーを対象に、サイト内ポイント還元率の上乗せを行う月間キャンペーンを実施しました。コア層のエンゲージメントをさらに向上させることを目的としています。なお、このキャンペーンは事前予告されていなかったと仮定します。
施策が終了し、今後同様のキャンペーンを実施するか判断するにおいて、今回の施策の効果の測定が大変重要である状況にあります。
まず、この人工データを作成します。作成するカラムは、施策期間(1か月)中の購買金額、施策前月までの1年間の月あたりの平均購入金額です。さらに共変量のチェックのために、年齢を作成します。
今回は、施策には1か月の購買金額を3500円増加させる効果を持つと仮定します。
#パッケージ
library(rdrobust)
library(rddensity)
library(ggplot2)
set.seed(123)
#サンプルサイズ(n=1000)
n <- 1000
#年齢(20歳から50歳)
age <- sample(20:50, n, replace = TRUE)
#前月の購入額(平均2000円、標準偏差2500円の正規分布に従う、誤差 ±1000円 を加え、0 円で打ち切り)
lastmonth_purchase_amount <- rnorm(n, mean = 2000, sd = 2500)
lastmonth_purchase_amount <- pmax(0, lastmonth_purchase_amount + runif(n, min = -1000, max = 1000))
#施策期間中のデータ
#施策期間中の購入金額
#全員の購入額を作成(平均2000円、標準偏差3500円)
purchase_amount <- rnorm(n, mean = 2000, sd = 3500)
#施策対象者には3500円+誤差(標準偏差1000円)を加える
purchase_amount <- ifelse(lastmonth_purchase_amount >= 2500,
purchase_amount + rnorm(n, mean = 3500, sd = 3000),
purchase_amount)
#0円で打ち切り
purchase_amount <- pmax(0, purchase_amount)
data <- data.frame(
age = age,
lastmonth_purchase_amount = lastmonth_purchase_amount,
purchase_amount = purchase_amount
)
次に、施策が施策期間中の購買金額に与える効果を推定します。
rdrobust::rdrobust(y = data$purchase_amount,
x = data$lastmonth_purchase_amount, c=2500, all = TRUE) |>
summary()

rdrobustを用いて、推定量を算出しました。なお、引数で"all = True"を指定することで、従来の信頼区間に加え、従来のMSEに基づく推定値から漸近バイアス推定量を引いた推定値を用いたバイアス修正済み信頼区間が示されています。漸近バイアス推定量の算出に用いたバンド幅は、"BW bias (b)"として報告されています。また、これまで述べてきたバイアスにrobustな信頼区間も最終行に報告されています。詳しい議論は川口、澤田(2024)P163~P170を参照ください。
この報告から、平均処置効果の推定量が従来の推定方法で4046.966、バイアス修正済みの推定において4206.975であり、想定していた3500という値と(若干誤差があるものの)近い値となっていることがわかります。
rdrobust::rdplot(y = data$purchase_amount,
x = data$lastmonth_purchase_amount, c=2500)

実際に値と回帰線をプロットすると、カットオフにおいてジャンプが起こっているのが分かります。(人工データとは言え、さすがに露骨すぎましたかね。)
加えて、密度関数のプロットも試みましたが、今回は打ち切りの影響で前月の購入金額が0である値が多く、95%信頼区間が見にくい図になってしまったため、報告は省略します。
妥当性の確認
RDDの妥当性の確認に関して、川口、澤田(2024)「因果推論の計量経済学」と安井、伊藤、金子(2024)、ともに②を確認するためのMcCrary検定、③を確認するための共変量バランスの方法を紹介しています。これらに倣って、今回この2つの方法を実施してみようと思います。
McCrary検定
この検定では、カットオフ値直前の密度関数がカットオフ値直後の密度関数と一致することを帰無仮説、一致しないことを対立仮説としています。この帰無仮説が棄却されると、RDDの条件②が満たされないこととなります。
rddensity(X = data$purchase_amount, c=2500) |> summary()

Robustの欄において、P値が算出されています。この値から、帰無仮説が10%有意水準でも棄却されないことがわかります。
共変量バランス
次に、共変量バランスをチェックします。ここではobservable factorsとして年齢を採用します。
rdrobust::rdrobust(y = data$age,
x = data$lastmonth_purchase_amount, c=2500, all = TRUE) |>
summary()
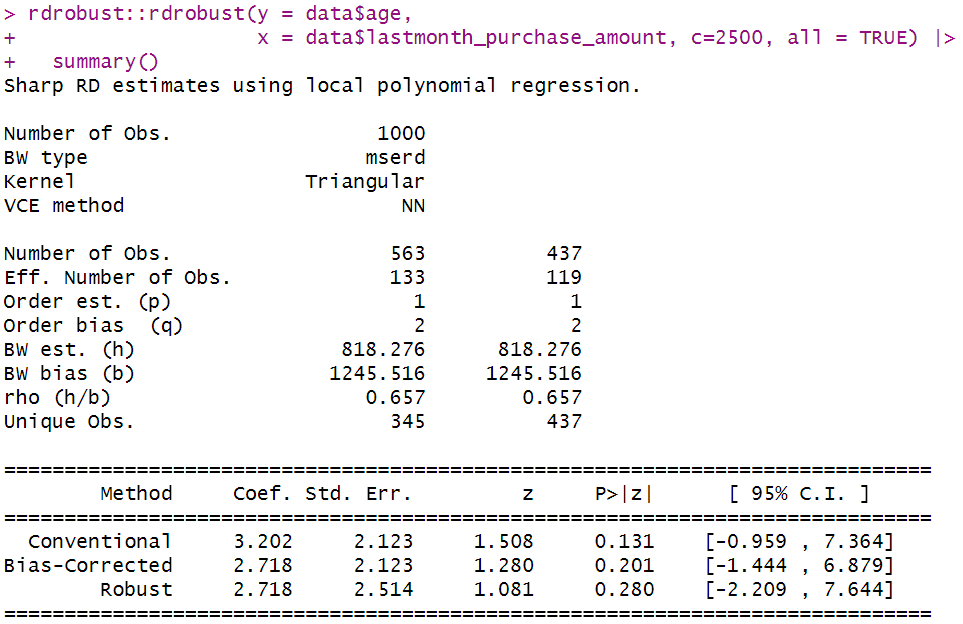
今回は目的変数に年齢を置き、本推定同様にRDDを実装しました。結果として有意な結果は得られませんでした。
これらの結果を参考に②と③を確かめ、RDDの妥当性を確かめます。
まとめ
今回はRDDのうちrdrobustパッケージを用いた推定を紹介しました。
実際の施策ケースでは、RDDが適当ではない場合も存在すると思います。安井、伊藤、金子(2024)では、RDDが成立しないケースとして操作が存在するケースを挙げています。例えば今回想定したケースのように前月の購入額etcによってポイント還元率が上昇するキャンペーンが前もってアナウンスされていた場合、カットオフ値をぎりぎり超えるユーザーの多くを潜在的に購買意欲の高いユーザーが占める可能性もあり、このときカットオフ値の近傍で処置および統制を決定するのはランダムではなく、(観測不可能なものも含め)共変量が影響する可能性があると思います。
安井、伊藤、金子(2024)ではこれに加えてFuzzy RDDやbunchingの議論等が、川口、澤田(2024)ではFuzzy RDDや離散スコアを用いたRDDに関する議論等が紹介されています。なお、安井、伊藤、金子(2024)ではMcCrary検定と共変量バランスの検定をクリアしても条件②と③が満たされないケースについても解説されています。両者を補完的に用いながら勉強していければと思います。
Discussion