🦎

モンテカルロ法による3体相互作用を持つ全結合イジング模型の解析

pagliacci

2023/12/22に公開

Python

physics

tech

はじめに

この記事はJij Inc. Advent Calendar 2023の22日目の記事です。
株式会社Jijの鈴木です。

この記事では、3体相互作用を持つ全結合イジング模型を古典モンテカルロ法を用いて数値的に解析します。以前に書いた記事で、3体相互作用を含む一般の高次相互作用を持つ全結合イジング模型に対して解析的なアプローチを行い、1次相転移を起こすことが分かりました。つまりこのモデルの性質はある程度分かっているわけですが、この記事ではそのことを数値的に検証します。

モデル

3体相互作用を持つ全結合イジング模型は以下で定義されます。

E_{p=3}=-\frac{2}{(N-1)(N-2)}\sum^{N}_{i=1}\sum^{N}_{j=i+1}\sum^{N}_{k=j+1}\sigma_{i}\sigma_{j}\sigma_{k}

ここで、 $N$ は全スピン数、 $\sigma_{i}\in\{-1, +1\}$ はスピン変数です。また、 $\frac{2}{(N-1)(N-2)}$ は相互作用の規格化定数であり、ある一つのスピンと相互作用しているスピンの総数で割っています。
以下ではこのモデルの数値シミュレーション結果を示します。

モンテカルロ法による結果

シミュレーション手法として、シングルスピンフリップによるメトロポリス法^[1]を用いました。この手法の解説は行いませんが非常に基本的なアルゴリズムの一つです。以下ではこの手法によるシミュレーション結果を示します^[2]。

磁化

この系の磁化 $m$ は以下で定義されます。

m=\frac{1}{N}\sum^{N}_{i=1}\braket{\sigma_{i}}

ここで、スピンの期待値 $\braket{\sigma_{i}}$ はカノニカル分布のもとでは、

\braket{\sigma_{i}}=\frac{1}{Z}\sum_{\sigma_{1}=\pm 1}\sum_{\sigma_{2}=\pm 1}\cdots\sum_{\sigma_{N}=\pm 1}\sigma_{i}\exp(-\beta E_{p=3})

となります。 $Z$ は分配関数です。
磁化 $m$ は系がどの程度磁石になっているかを示す量で、 $m>0$ なら磁石としての性質を持っていると言えます。 $m=0$ から $m>0$ に変化する温度 $T_{\rm c}=1/\beta_{\rm c}$ はこの系が磁石ではない常磁性相から磁石である強磁性相に変化する温度であり、転移温度と呼ばれます。
さて、この磁化を直接計算せずにモンテカルロシミュレーションで推定するには以下の式を用います。

m_{\rm MC}=\braket{m}_{\rm MC}=\frac{1}{M}\sum^{M}_{j=1}m_{j}=\frac{1}{M}\sum^{M}_{j=1}\frac{1}{N}\sum^{N}_{i=1}\sigma^{(j)}_{i}

ここで、 $\sigma^{(j)}_{i}$ はスピン $i$ の $j$ 番目のサンプリング結果を表します。よって、

m_{j}=\frac{1}{N}\sum^{N}_{i=1}\sigma^{(j)}_{i}

は $j$ 番目のサンプルによって得られた系の磁化を表しています。サンプリングは全部で $M$ 回行うため、この $m_{j}$ に対してサンプル平均を取ったのが $m_{\rm MC}$ ということになります。それでは以下に結果を示します。

3体全結合イジング模型に対するメトロポリス法による磁化の計算結果(左図)とその理論値(右図)。メトロポリス法のサンプル数は $M=10000$ , sweep数は10000。

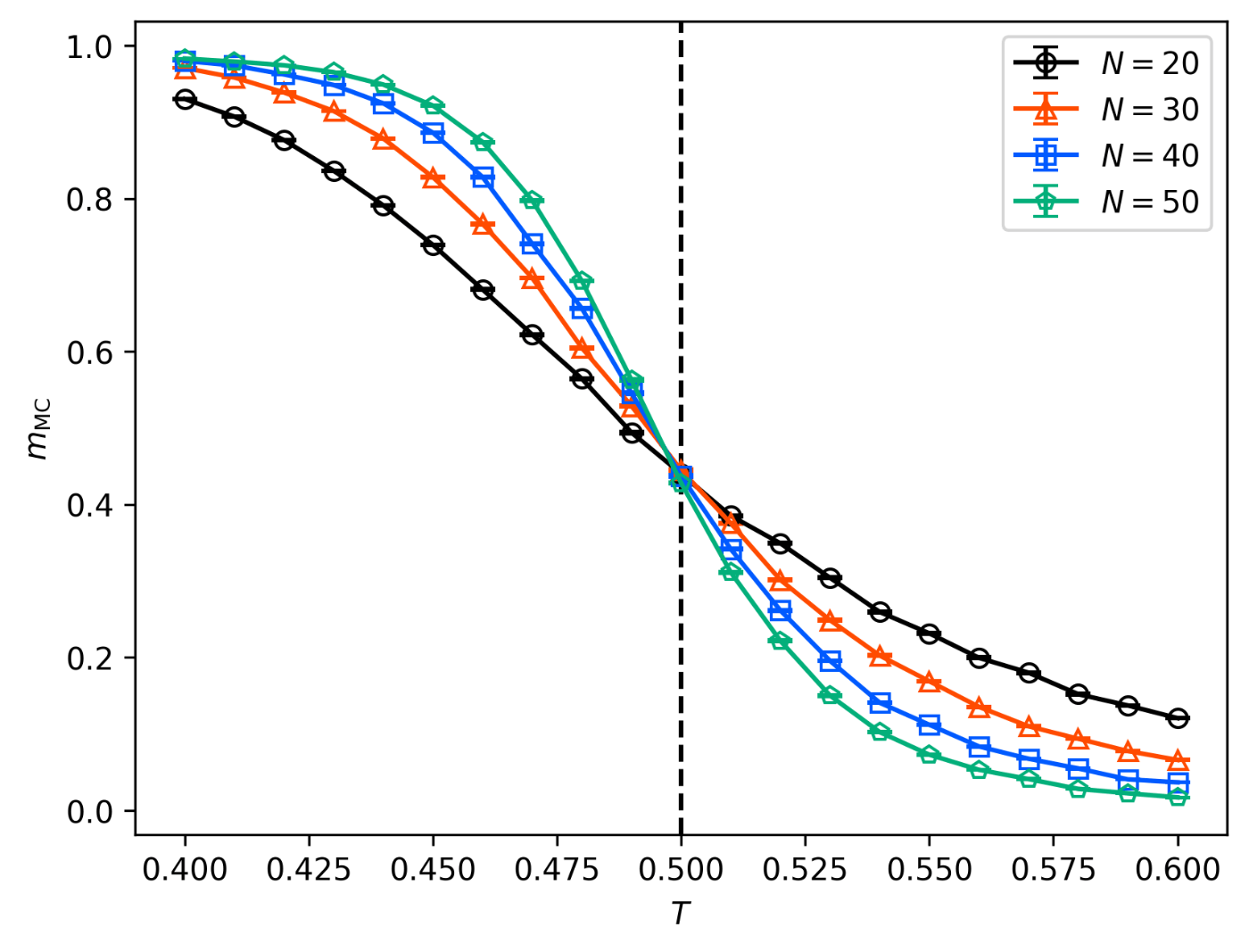
左の図がシミュレーション結果であり、標準誤差をエラーバーとして付けていますが非常に小さいです。右の図は以前に計算した熱力学極限( $N\rightarrow\infty$ )での理論値です。シミュレーション結果はおおよそ理論値と同様の振る舞いをしており、 $T\simeq 0.5$ くらいで $m>0$ となり相転移の兆候が見えます。 $N$ を大きくすると磁化の変化がシャープになり、理論値の振る舞いに近づいていくことも分かります^[3]。
$T\simeq 0.5$ 近傍でデータを細かく取ると以下のようになりました。なお、転移温度はより正確には $T_{\rm c}\simeq 0.496$ となります。

3体全結合イジング模型に対するメトロポリス法による転移温度近傍の磁化の計算結果。メトロポリス法のサンプル数は $M=20000$ , sweep数は20000。
系の大きさ $N$ が小さいため、転移温度を境に急激に磁化が立ち上がる1次転移のような兆候はあまり見えませんが、 $N$ を大きくしていけば $T_{\rm c}\simeq 0.496$ あたりで磁化の立ち上がりがシャープになっていく傾向が見て取れます。

ビンダー比

転移温度を検出するために以下のビンダー比の計算を行いました。

U_{\rm MC}=1 - \frac{\braket{m^4}_{\rm MC}}{3\braket{m^2}^2_{\rm MC}}

ここで、磁化の２乗と4乗の期待値はそれぞれ

\braket{m^2}_{\rm MC}=\frac{1}{M}\sum^{M}_{j=1}m^2_{j},\;\;\braket{m^4}_{\rm MC}=\frac{1}{M}\sum^{M}_{j=1}m^4_{j}

と定義されます。この量は相転移点直上でシステムサイズ依存性がなくなる量であり、この量をプロットして交わったところが転移点ということになります。最も今回のケースでは上で見たように磁化 $m$ の温度依存性をプロットした段階で、転移点が $T_{\rm c}\simeq 0.5$ 程度の場所にあることは分かっています。ビンダー比のプロットでも同様の傾向化見えるはずです。

3体全結合イジング模型に対するメトロポリス法による転移温度近傍のビンダー比 $U_{\rm MC}$ の計算結果。サンプル数 $M=10000$ , sweep数10000の実験を10回行い平均を取った。エラーバーは10回の実験における標準偏差。

確かに $T\simeq 0.5$ より少し小さいところで全てのデータが一点で交わっていることが分かります。やはりここで相転移を起こしていると言えそうです。また、特に興味深いのは転移温度より少し高いところでビンダー比が大きく負の値を取っていることです。実はこれは一次転移の特徴であり、他の一次転移を起こす系でも同様の兆候が見れます^[4]。という訳で、どうやらこの系は一次転移を起こしていそうなことが分かりました。これは過去の記事で行った理論解析の結果と一致しています。

OpenJijを用いた計算

この節では上で行った計算結果を再現するためのソースコードを示します。株式会社Jijが開発しているオープンソースソフトウェアであるOpenJijを用いたコードを紹介します。ただし、OpenJijを用いた場合、ここで考えている3体全結合イジング模型ではメトロポリス法によって一つのスピンをアップデートする際に $O(N^2)$ の計算量が必要となり計算に時間がかかってしまいます^[5]。
実は、3体全結合イジング模型に特化した計算を行えば一つのスピンのアップデートを $O(N)$ で行うことができます^[6]。今回載せた結果は全てこのやり方で行っておりOpenJijは使っていません。とはいえ以下に示すコードでも計算時間にさえ目をつぶれば同じ結果を再現するはずです。

シミュレーション

OpenJijの使い方についてはこちらを参照してください。ここでは詳細な説明は行いません。必要なライブラリ、openjij、numpy、tqdmはあらかじめインストールしておいてください。
まず、最も重要なシミュレーション部分のコードを示します。
なお、以下でnum_threads=4という部分がありますが、このオプションを指定することで各サンプリングを並列に行ってくれます。ただしMac環境はこれに対応していません^[7]。

import openjij as oj
import numpy as np
from tqdm import tqdm # プログレスバー表示するためのライブラリ

num_samples = 1000 # サンプル数。計算が遅いので小さくしてあります。
num_sweeps = 1000 # サンプリング数。計算が遅いので小さくしてあります。
T_list = np.linspace(0.1, 1.1, 11) # 温度のリスト
N_list = [20, 30, 40, 50] # システムサイズNのリスト

sample_list_N = []
for N in N_list:
    # 相互作用の格納
    J = {}
    for i in range(N):
        for j in range(i+1, N):
            for k in range(j+1, N):
                J[(i, j, k)] = -2/((N - 1)*(N - 2))

    # サンプリング
    sample_list = []
    for T in tqdm(T_list):
        sample = oj.SASampler().sample_hubo(
            J=J, 
            num_sweeps=num_sweeps, 
            num_reads=num_samples, 
            vartype="SPIN", 
            beta_max=1/T, 
            beta_min=1/T, 
            num_threads=4
        )
        sample_list.append(sample)
    sample_list_N.append(sample_list)

ちなみにRyzen7950xを用いて32並列(上記のコードでnum_threads=32とした)で計算を行ったところ、私の環境では全体で2分30秒かかりました。

磁化とビンダー比

サンプリングが終了したら各物理量を計算します。系の磁化 $\braket{m}_{\rm MC}$ とビンダー比 $U_{\rm MC}$ を計算する関数は以下のようになります。

def calculate_magnetization(sample: oj.Response):
    # 磁化を計算するして、平均と標準誤差を返す
    mag_list = [np.mean(r[0]) for r in sample.record]
    return np.mean(mag_list), np.std(mag_list)/np.sqrt(len(mag_list))
   
def calculate_binder_ration(sample: oj.Response, split = 10):
    # サンプルを(デフォルトで)10ごとに区切って各区間でビンダー比を計算し、
    # その平均と標準偏差を返す
    binder_list = []
    for i in range(split):
        split_start = i*len(sample.record)//split
        split_end = (i + 1)*len(sample.record)//split
        m_list = [np.mean(s[0]) for s in sample.record[split_start:split_end]]
        m2 = np.mean([m**2 for m in m_list])
        m4 = np.mean([m**4 for m in m_list])
        binder_list.append(1 - m4/(3*m2**2))

    return np.mean(binder_list), np.std(binder_list)

グラフの描画

これらの関数を使って、以下のようにグラフを書きました。matplotlibをインストールする必要があります。

import matplotlib.pyplot as plt

# 磁化の描画
mag_1 = [calculate_magnetization(sample) for sample in sample_list_N[0]]
mag_2 = [calculate_magnetization(sample) for sample in sample_list_N[1]]
mag_3 = [calculate_magnetization(sample) for sample in sample_list_N[2]]
mag_4 = [calculate_magnetization(sample) for sample in sample_list_N[3]]

plt.errorbar(T_list, [m[0] for m in mag_1], yerr=[m[1] for m in mag_1], marker='o', capsize=4, fillstyle='none', color=[0,0,0], label='$N=20$')
plt.errorbar(T_list, [m[0] for m in mag_2], yerr=[m[1] for m in mag_2], marker='^', capsize=4, fillstyle='none', color=[1,75/255,0/255], label='$N=30$')
plt.errorbar(T_list, [m[0] for m in mag_3], yerr=[m[1] for m in mag_3], marker='s', capsize=4, fillstyle='none', color=[0,90/255,255/255], label='$N=40$')
plt.errorbar(T_list, [m[0] for m in mag_4], yerr=[m[1] for m in mag_4], marker='p', capsize=4, fillstyle='none', color=[3/255, 175/255, 122/255], label='$N=50$')
plt.xlabel('$T$')
plt.ylabel(r'$m_{\rm MC}$')
plt.axvline(x=0.5, color=[0,0,0], linestyle='--')
plt.legend()
plt.show()

# ビンダー比の描画
bind_1 = [calculate_binder_ration(r) for r in sample_list_N[0]]
bind_2 = [calculate_binder_ration(r) for r in sample_list_N[1]]
bind_3 = [calculate_binder_ration(r) for r in sample_list_N[2]]
bind_4 = [calculate_binder_ration(r) for r in sample_list_N[3]]

plt.errorbar(T_list, [m[0] for m in bind_1], yerr=[m[1] for m in bind_1], capsize=4, fillstyle='none', marker='o', color=[0,0,0], label='$N=20$')
plt.errorbar(T_list, [m[0] for m in bind_2], yerr=[m[1] for m in bind_2], capsize=4, fillstyle='none', marker='^', color=[1,75/255,0/255], label='$N=30$')
plt.errorbar(T_list, [m[0] for m in bind_3], yerr=[m[1] for m in bind_3], capsize=4, fillstyle='none', marker='s', color=[0,90/255,255/255], label='$N=40$')
plt.errorbar(T_list, [m[0] for m in bind_4], yerr=[m[1] for m in bind_4], capsize=4, fillstyle='none', marker='p', color=[3/255, 175/255, 122/255], label='$N=50$')
plt.axvline(x=0.5, color=[0,0,0], linestyle='--')
plt.xlabel('$T$')
plt.ylabel(r'$U_{\rm MC}$')
plt.legend()
plt.show()

まとめ、今後について

3体相互作用を持った全結合イジング模型に対してモンテカルロ法を用いて磁化とビンダー比の温度依存性を計算しました。結果、磁化とビンダー比の振る舞いからこの系が $T\simeq 0.5$ 付近で相転移を起こしていることが分かりました。さらにビンダー比が転移点よりわずかに高温側で大きく負の値を取ることから、この相転移は1次転移であることが示唆されました。これらの結果は以前行った解析の結果と整合しています。
今回は参考としてOpenJijを用いたサンプルコードを載せましたが、全結合イジング模型に限定すればより高速にシミュレーションを行うことができます。次回はそれについて書こうと思います。

＼Rustエンジニア・数理最適化エンジニア募集中！／

株式会社Jijでは、数学や物理学のバックグラウンドを活かし、量子計算と数理最適化のフロンティアで活躍するRustエンジニア、数理最適化エンジニアを募集しています！
詳細は下記のリンクからご覧ください。皆さんのご応募をお待ちしております！
Rustエンジニア: https://open.talentio.com/r/1/c/j-ij.com/pages/51062
数理最適化エンジニア: https://open.talentio.com/r/1/c/j-ij.com/pages/75132

脚注

例えば、こちらの記事を参照してください。 ↩︎
本来はサンプル数やsweep数が足りているか議論する必要がありますが、この記事ではそのようなことは行っていません。何故かと言えばそれはとても面倒、、、というのが本音ですが、あえて言えばここでの目的はラフに相転移の傾向を捉えることであり、実際に相転移の傾向は見えています。 ↩︎
シミュレーション結果に対して $N$ 無限大の結果を外挿することで、 $N$ が大きい極限の振る舞いを見ることができます。 ↩︎
例えば、Phys. Rev. B 30, 1477の図4,Phys. Rev. E 101, 052102の図8、Phys. Rev. B 103, 075147の図2(c)、
Phys. Rev. E 99, 023309の図9、10、13、14などで同様の傾向が見られます。 ↩︎
これはOpenJijの実装が悪いわけではなく汎用性のためです。OpenJijは一般の高次相互作用かつ任意の相互作用係数を持ったイジング模型を受け入れることができます。 ↩︎
p体全結合イジング模型に対して $O(pN)$ で計算することができます。 ↩︎
Macの場合でも、OpenMPを自分で入れてOpenJijのcmakeを適切に書き換えれば並列化が有効になります。 ↩︎

Jij Tech BlogPublication