概要
この記事では全結合イジング模型において、相互作用を一般の多体相互作用に拡張した模型の相転移について考えます。相互作用は一様で強磁性的なものを仮定します。このモデルについては検索してもあまりヒットしないのですが、モデルの性質自体はすでによく知られており、相互作用の次数をpとしてp>2で一次転移を示すことが分かっています。この記事ではこのことを確認します。
ちなみにどうしてこのような模型に興味を持ったかというと、自分はJijに入社した当初、高次制約なし二値最適化問題に対してシミュレーテッドアニーリングを行うソルバーを開発していたのですが、その際にソルバーが正しい挙動をしているか確かめるために厳密解の分かる模型が欲しくなり、ここで議論するような模型を考えたのがきっかけです。
モデル
一般の場合
高次相互作用を持った全結合イジング模型は以下で定義されます。
E_{p}=-\frac{1}{\binom{N-1}{p-1}}\sum^{N}_{i_1=1}\sum^{N}_{i_2=i_1+1}\cdots\sum^{N}_{i_p=i_{p-1}+1}\sigma_{i_1}\sigma_{i_2}\cdots\sigma_{i_p}
ここで、Nは全スピン数、\sigma_{i_j}\in\{-1, +1\}はスピン変数、pは相互作用の次数であり、
\binom{N-1}{p-1}=\frac{(N-1)(N-2)\cdots(N-p+1)}{(p-1)(p-2)\cdots 1}
は相互作用の規格化定数です。この規格化定数は自由エネルギーがスピン数Nに対して示量的になるように決めればよく、いくらかの任意性があります。ここでは以降の計算が簡単になるように\binom{N-1}{p-1}としており、例えばN^{p-1}としてもNが大きい極限では温度が適当にスケールされるだけで基本的な性質は変わりません。ちなみに\binom{N-1}{p-1}はある一つのスピンと相互作用しているスピンの総数になっています。
3体相互作用の場合
この記事では主にp=3のモデルを考えます。ハミルトニアンは以下のとおりです。
E_{p=3}=-\frac{2}{(N-1)(N-2)}\sum^{N}_{i=1}\sum^{N}_{j=i+1}\sum^{N}_{k=j+1}\sigma_{i}\sigma_{j}\sigma_{k}
ここで、便利のために以下の全スピンの和を定義しておきます。
\Psi=\sum^{N}_{i=1}\sigma_{i}
この量の3乗を計算すると、
\Psi^3=\sum^{N}_{i=1}\sum^{N}_{j=1}\sum^{N}_{k=1}\sigma_{i}\sigma_{j}\sigma_{k}\\
=\sum^{N}_{i=1}\sigma^3_{i} + 3\sum^{N}_{i=1}\sum^{N}_{\substack{j=1 \\ i \neq j}}\sigma^2_{i}\sigma_{j}+\sum^{N}_{i=1}\sum^{N}_{j=1}\sum^{N}_{\substack{k=1 \\ i \neq j \neq k}}\sigma_{i}\sigma_{j}\sigma_{k}\\
=\sum^{N}_{i=1}\sigma^3_{i}+3\left(\sum^{N}_{i=1}\sum^{N}_{j=1}\sigma^2_{i}\sigma_{j} - \sum^{N}_{i=1}\sigma^3_{i}\right) + 6\sum^{N}_{i=1}\sum^{N}_{j=i+1}\sum^{N}_{k=j+1}\sigma_{i}\sigma_{j}\sigma_{k}\\
=\Psi+3(N\Psi - \Psi)+6\sum^{N}_{i=1}\sum^{N}_{j=i+1}\sum^{N}_{k=j+1}\sigma_{i}\sigma_{j}\sigma_{k}\\
=(3N-2)\Psi+6\sum^{N}_{i=1}\sum^{N}_{j=i+1}\sum^{N}_{k=j+1}\sigma_{i}\sigma_{j}\sigma_{k}
となります。ここで\sigma^2_{i}=1を使いました。上記関係式を用いるとハミルトニアンを\Psiの関数として表現できて、
E_{p=3}=-\frac{1}{3(N-1)(N-2)}\left\{\Psi^3-(3N-2)\Psi\right\}
となります。
分配関数の計算
上の式を分配関数の定義に代入すると、
Z = \sum_{\sigma_{1}=\pm 1}\sum_{\sigma_{2}=\pm 1}\cdots\sum_{\sigma_{N}=\pm 1}\exp\left(-\beta E_{p=3}\right)\\
=\sum_{\sigma_{1}=\pm 1}\sum_{\sigma_{2}=\pm 1}\cdots\sum_{\sigma_{N}=\pm 1}\exp\left[\frac{\beta}{3(N-1)(N-2)}\{\Psi^3-(3N-2)\Psi\}\right]
となります。ここで全てのスピンについての和、\sum_{\sigma_{1}=\pm1}\cdots\sum_{\sigma_{N}=\pm1}について、個別に和を取るのではなく、全スピン\Psiで和をとるように書き換えることができます。
Z=\sum^{N}_{\Psi=-N}W(\Psi)\exp\left[\frac{\beta}{3(N-1)(N-2)}\{\Psi^3-(3N-2)\Psi\}\right]
ここで新しく現れたW(\Psi)は全スピンの値が\Psiとなる場合の数であり以下のようになります。
W(\Psi)=\left\{
\begin{array}{ll}
\frac{N!}{\left(\frac{N+\Psi}{2}\right)!\left(\frac{N-\Psi}{2}\right)!} & N\pm\Psiが0以上の偶数の時 \\
0 & 上記以外
\end{array}
\right.
Nが十分大きいとしてスターリングの公式\log N!\simeq N\log N - Nを適用すると、N\pm\Psiが0以上の偶数の時、
\log W(\Psi)=\log N! - \log\left(\frac{N+\Psi}{2}\right)!-\log\left(\frac{N-\Psi}{2}\right)!\\
\simeq N\log N - N - \left(\frac{N+\Psi}{2}\log\frac{N+\Psi}{2} - \frac{N+\Psi}{2}\right) - \left(\frac{N-\Psi}{2}\log\frac{N-\Psi}{2} - \frac{N-\Psi}{2}\right)\\
=-\frac{N}{2}\left\{\left(1+\frac{\Psi}{N}\right)\log\left(1+\frac{\Psi}{N}\right)+\left(1-\frac{\Psi}{N}\right)\log\left(1-\frac{\Psi}{N}\right)-2\log 2\right\}
となります。ここで新たにスピンあたりの磁化
および、
\sigma(\psi)=\log2 - \frac{1}{2}\left\{(1+\psi)\log(1+\psi)+(1-\psi)\log(1-\psi)\right\}
を定義すると、
\log W(\Psi) \simeq N\sigma(\psi)
となるので、これの\logを外して、
W(\Psi)\simeq \exp\left(N\sigma(\psi)\right)
という関係式を分配関数の表式に代入してNが十分大きいとすると、
Z=\sum^{N}_{\Psi=-N}W(\Psi)\exp\left[\frac{\beta}{3(N-1)(N-2)}\{\Psi^3-(3N-2)\Psi\}\right]\\
\simeq \frac{N}{2}\int^{1}_{-1}\exp\left[\frac{\beta}{3(N-1)(N-2)}\{\Psi^3-(3N-2)\Psi\}+N\sigma(\psi)\right]d\psi\\
=\int^{1}_{-1}\exp N\left[\frac{\beta}{3N(N-1)(N-2)}\{\Psi^3-(3N-2)\Psi\}+\sigma(\psi)+\frac{1}{N}\log\frac{N}{2}\right]d\psi\\
\simeq\int^{1}_{-1}\exp N\left[\frac{\beta\psi^3}{3}+\sigma(\psi)\right]d\psi
と評価することができます。ここで、Nが十分大きいとして
\sum^{N}_{\Psi=-N}\rightarrow \frac{N}{2}\int^{1}_{-1}d\psi
と、和を積分で書き換えています。
さて、次はこの積分を計算します。\sigma(\psi)の定義を代入してそのまま計算することは困難なので、ラプラスの方法を使って評価します。つまり、上記積分値に寄与するのは指数関数の中が最大値を取るときなので、
f(\psi)=\frac{\beta \psi^3}{3}+\sigma(\psi)
と、指数関数の中でNに比例する項をまとめると、
Z\simeq\int^{1}_{-1}\exp Nf(\psi)\sim \exp\left(Nf(\psi^*)\right)\sqrt{\frac{2\pi}{N|f''(\psi^*)|}}
と形式的に書くことができます。ここで、
f(\psi^*)=\max_{-1\leq \psi \leq 1}\{f(\psi)\}
であり、\psi^*は関数f(\psi)の最大値を与える量です(ただし、この表記では最大値を与える\psiが唯一であると仮定しています)。
磁化の計算
分配関数の計算過程で出てきた\psi^*という量が実はこの系の磁化に対応する量であることがわかります。
よって、f(\psi)の最大値を与える\psiの\beta依存性が重要になります。それが分かれば任意の温度T=1/\betaでの磁化の値が分かることになります。
関数f(\psi)の定義はその定義域を-1\leq\psi\leq1として、
f(\psi)=\frac{\beta \psi^3}{3}+\log2 - \frac{1}{2}\left\{(1+\psi)\log(1+\psi)+(1-\psi)\log(1-\psi)\right\}
でした。最大値を与える\psiの候補は以下の方程式で与えられます。
f'(\psi)=\beta \psi^2+\frac{1}{2}\log\frac{1-\psi}{1+\psi}=0\\
\Rightarrow \psi=\tanh(\beta \psi^2)
これは平均場近似による自己整合方程式とよく似ています。実際、ハミルトニアンE_{p=3}において\sigma_{i}\rightarrow m+\delta\sigma_{i}という置き換えを行い\delta\sigma_{i}の二次以上の項を落とすと上記方程式が得られます。
通常の2体相互作用を持ったイジング模型における自己整合方程式は\psi=\tanh(\beta \psi)となるので、\psiの次数が一つ大きくなったことが違いとなっています。
ここから先は実際にf(\psi)のグラフを書いてみて磁化m=\psi^*の挙動を確認していきます。
先程、f(\psi)の定義域は-1\leq\psi\leq1と述べましたが、今考えている系は3体相互作用を持っているため、スピン反転対称性\sigma\rightarrow -\sigmaを持たず、低温では明らかに磁化は正の値を取ることが分かります。よって、以下ではf(\psi)の定義域を0\leq\psi\leq1に制限します。
以下に\beta=1.5,1.7,1.8,2.3という典型的な逆温度での関数形を示しました。また、念のためソースコードも載せておきました。
import matplotlib.pyplot as plt
import numpy as np
beta=2.3
x = np.arange(0, 1.1, 0.1)
y1 = x
y2 = np.tanh(beta*x*x)
plt.plot(x, y1, label=r"$y=\psi$", color="black")
plt.plot(x, y2, label=r"$y=\tanh(\beta\psi^2),\beta=$"+f"{beta}", color="red")
plt.xlabel(r'$\psi$')
plt.xlim([0, 1])
plt.ylim([0, 1])
plt.legend()
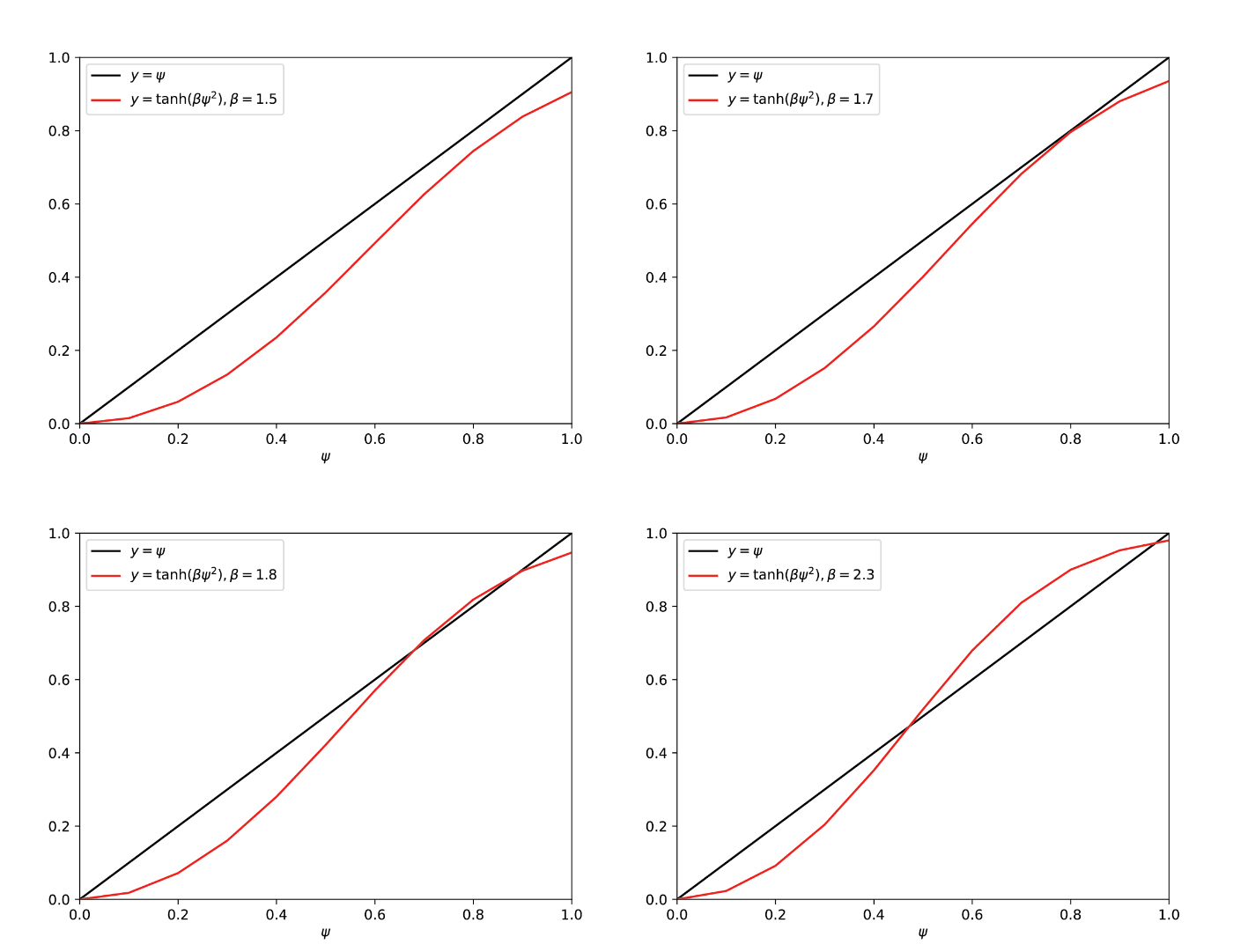
ここから、\psi=\tanh(\beta \psi^2)という方程式は\beta\lesssim 1.7で\psi=0、\beta\sim 1.7で\psi=0と\psi\sim 0.8という2つの解を持ち、\beta\gtrsim 1.7では3つの解を持つことが分かります。\beta\gtrsim 1.7における\psi=0と\betaの増大にともなって単調減少する2つの解は、非物理的なためこれ以降は考察しません。
さて、上記の考察からこの系の磁化は
-
\beta\lesssim 1.7ではゼロ
-
\beta\gtrsim 1.7で\psi\sim 0.8という値に不連続に変化し、以後\betaの増大にともなって増加していく
という振る舞いをすることが分かりました。したがってこの系は一次転移を示すことが示唆されます。
しかし、ここで一つ注意しなければいけない点があります。というのも\psi=\tanh(\beta \psi^2)という方程式の解は、f(\psi)の最大値を与える単なる候補であるということです。そこで、先程と同じ\betaに対して今度はf(\psi)のグラフを書いてみます。
import matplotlib.pyplot as plt
import numpy as np
beta=2.3
x = np.arange(0, 1, 0.001)
y = beta*x*x*x/3+np.log(2)-0.5*((1+x)*np.log(1+x)+(1-x)*np.log(1-x))
plt.plot(x, y, label=r"$y=f(\psi),\beta=$"+f"{beta}", color="black")
plt.xlabel(r'$\psi$')
plt.xlim([0, 1])
plt.ylim([0.4, 0.8])
plt.legend()
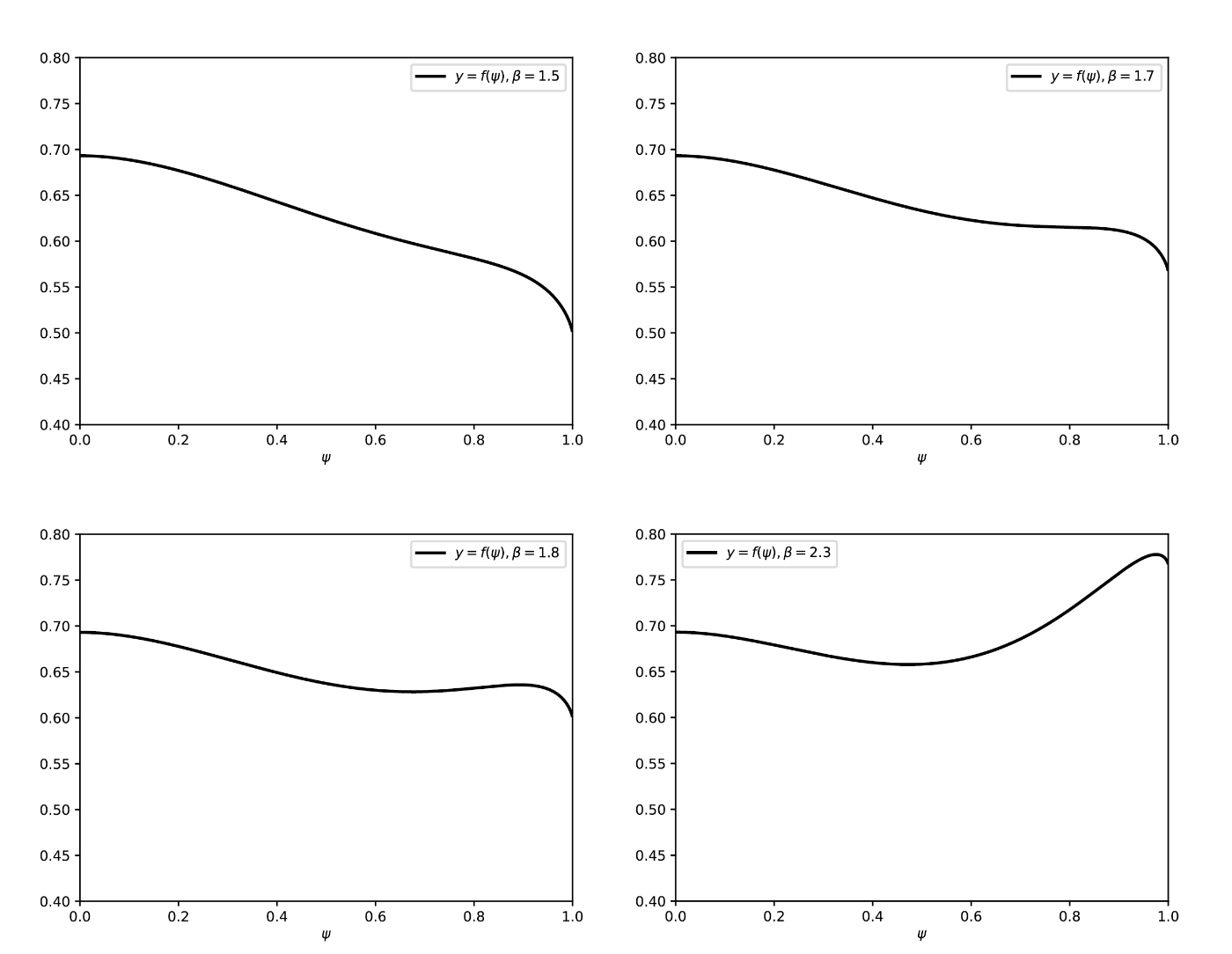
結果は一目瞭然です。自己整合方程式は\beta\sim 1.8では明らかに有限の解を持っていましたが、もとの関数f(\psi)は\beta=1.8では\psi=0で最大値を取っていることが分かります。つまり、このときの磁化はまだゼロだということです。一方で\beta=2.3ではf(\psi)の最大値は有限の\psiが与えていることが分かるので、この系が一次転移を示すことは間違いなさそうです。先程の自己整合方程式の解による議論は転移温度T_{\text{c}}=1/\beta_{\text{c}}を過大評価していたことが分かりました。
最後に、磁化mの温度T依存性のグラフを書いてみます。
import matplotlib.pyplot as plt
import numpy as np
temperature_range = np.arange(0.1, 1.0, 0.001)
magnetization = []
for T in temperature_range:
beta = 1/T
x = np.arange(0, 1, 0.001)
y = beta*x*x*x/3+np.log(2)-0.5*((1+x)*np.log(1+x)+(1-x)*np.log(1-x))
magnetization.append(x[np.argmax(y)])
plt.scatter(temperature_range, magnetization, label="magnetization", color="black",s=10)
plt.xlabel(r'$T$')
plt.ylabel(r'$m$')
plt.legend()

およそT=0.5くらいで磁化が不連続に飛んでいることが分かります。確かに1次転移です。
一般のp体相互作用の場合の磁化
ここまではp=3の模型での議論でしたが、一般のp体相互作用の模型でもほとんど同様の議論をそのまま行うことができます。その結果、ハミルトニアン
E_{p}=-\frac{1}{\binom{N-1}{p-1}}\sum^{N}_{i_1=1}\sum^{N}_{i_2=i_1+1}\cdots\sum^{N}_{i_p=i_{p-1}+1}\sigma_{i_1}\sigma_{i_2}\cdots\sigma_{i_p}
で定まる系の磁化mの逆温度依存性は
f(\psi)=\frac{\beta \psi^p}{p}+\log2 - \frac{1}{2}\left\{(1+\psi)\log(1+\psi)+(1-\psi)\log(1-\psi)\right\}
という関数の最大値を与える\psiとなることが分かります。また、自己整合方程式は
\psi=\tanh(\beta \psi^{p-1})
となります。ただし、p=3の時と同様に磁化の値として採用する自己整合方程式の解は慎重に選ぶ必要があります。
最後に、グラフが重なってしまって少し見にくいですが、いくつかのpについての磁化mのグラフを載せておきます。
import matplotlib.pyplot as plt
import numpy as np
p_list=[2, 3, 4]
temperature_range = np.arange(0.1, 1.0, 0.001)
magnetization = []
for p in p_list:
temp_mag = []
for T in temperature_range:
beta = 1/T
x = np.arange(0, 1, 0.001)
y = beta*x**p/p+np.log(2)-0.5*((1+x)*np.log(1+x)+(1-x)*np.log(1-x))
temp_mag.append(x[np.argmax(y)])
magnetization.append(temp_mag)
for mag, p in zip(magnetization, p_list):
plt.scatter(temperature_range, mag, label=r"magnetization for $p=$"+f"{p}",s=10)
plt.xlabel(r'$T$')
plt.ylabel(r'$m$')
plt.legend()

まとめ
一様かつ強磁性的なp相互作用を持った全結合イジング模型の相転移について解析しました。その結果、p>2では一次転移を示すことが分かりました。
今後について
モンテカルロシミュレーションでここで行った解析結果が再現されるか確認してみたいと思います。
2023/12/22追記
モンテカルロシミュレーションの記事を書きました。
最後に
\Rustエンジニア・数理最適化エンジニア募集中!/
株式会社Jijでは、数学や物理学のバックグラウンドを活かし、量子計算と数理最適化のフロンティアで活躍するRustエンジニア、数理最適化エンジニアを募集しています!
詳細は下記のリンクからご覧ください。皆さんのご応募をお待ちしております!
Rustエンジニア: https://open.talentio.com/r/1/c/j-ij.com/pages/51062
数理最適化エンジニア: https://open.talentio.com/r/1/c/j-ij.com/pages/75132




Discussion