ディフィー・ヘルマン(DH)鍵共有についてのメモ
ディフィー・ヘルマン鍵共有とは、SSH接続などの際に使われる共通鍵を両端で安全に共有する方法です。このセッション鍵(共通鍵)は、セッション中のデータの暗号化と復号に使用されます。またこの共有鍵の原理として数学の離散対数の法則が使われています。離散対数についてよくわからない場合は以下にまとめてみましたのでご参照ください。
セッション鍵生成・交換プロセス
-
クライアントである数としてaという値を決めます。

-
サーバでもある数としてbという値を決めます。

-
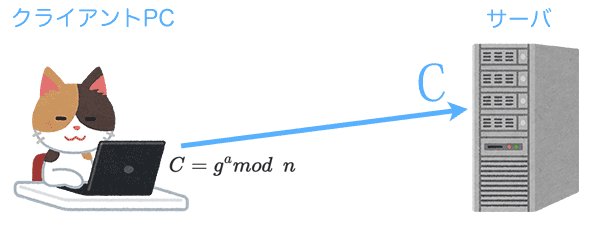
クライアントのaをある素数を交えた計算式、例えば
C = g^a mod\enspace n
-
サーバのbをある素数を交えた計算式、例えば
S = g^b mod\enspace n
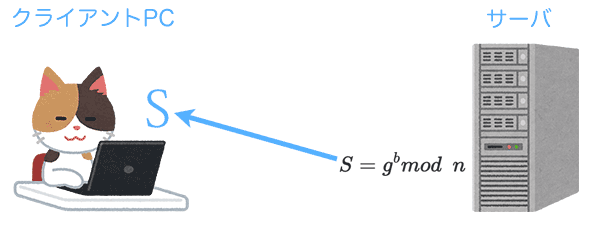
-
クライアントではaとSを使ってある計算をしaSという値を出します。
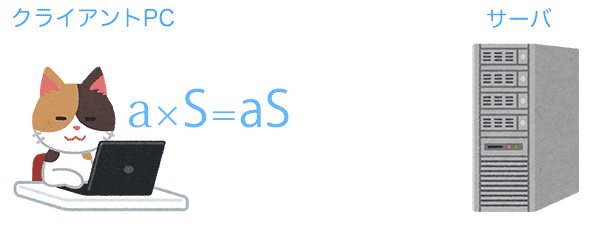
-
サーバではbとCを使ってある計算をしbCという値を出します。
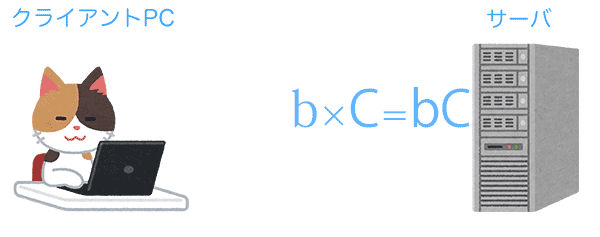
-
このaSとbCは同じ値になるのでこれが共通鍵になります。

この方法だと初回の通信時、つまりセキュアでない盗聴されている環境でも盗聴者が共通鍵の値を知ることは困難になります。それはある計算というのが普通に計算すれば短時間でできるのですが、逆算すると膨大な時間がかかるという離散対数問題という数学の原理を利用しているからです。
DHP(DH Problem)
実はディフィー・ヘルマン鍵交換アルゴリズムも完璧ではありません。論理的には前述の交換プロセスが全て盗聴されていて計算できれば共通鍵が判明するわけですね。ただこの計算は離散対数の性質で時間が膨大にかかるような法則があります。したがってこの膨大になる条件を満たしている必要があります。この条件もあくまでも現在の予測になりますが以下のように言われているようです。
mod n の部分のnが10進数で600桁以上、ビットに直すと2048の素数で、かつ、いくつかの条件を組み合わせれば今後20年くらいは解けないと仮設されているとのことでした。ディフィー・ヘルマン鍵交換アルゴリズムは基本的には安全ですが限界も物理的には存在しており、背景まで理解しておければベストですね。
ECDH鍵共有
DH鍵共有にさらに楕円離散対数問題(ECDLP)を絡めてセキュアにしたものとしてECDH鍵共有があります。私自身詳細は理解できていないので簡単にまとめますが、やっていることは基本的に前述の鍵生成・プロセスと同じでべき乗しているところをまた数学の性質であるECDLPを絡めて計算するというものになります。
またECDH鍵共有の大きな特徴として同じセキュリティレベルであればRSA暗号やDH鍵共有よりも短い鍵長で鍵を生成できます。そしてこれが高速化にも寄与します。
参考
とてもわかりやすく解説していただいておりました。(まだ深い部分は理解が浅いかもしれませんが💦)ありがとうございました。
Discussion