二変量正規分布の●●%領域と、一変量に落とした時の●●%区間の違い
これは何の記事か
Rで二変量確率分布の密度を可視化するときの注意というスクラップを書きながら調べているときにどこかの参考文献でFriendly et al. (2013)が挙げられていた。ellipsesに関する文献で結構奥が深くて全部は読み切れていないけれど、この中で気になったのが「(意訳)二変量正規分布の40%領域を各一変数写すと平均値±1標準偏差の区間になり、68%領域では平均値±1.5標準偏差の区間になる。」という説明(本当はこの68%領域と区間が一変量の時の平均値±1標準偏差の区間に相当するというような書き振りなのだけれどここはよく分からなかった)。
なぜこの説明に興味を持ったかというと、(多分)多重検定に関連することだから。一変量だけ見たい時と二変量で構成される全体があってその中で一つ一つを見たい時では、同じように考えてはいけないよ、という。この記事では上の標準偏差にかかる係数?がなぜ1と1.5になるのかということについて書いていく。標本分布上の信頼区間を書く際にも、関心のあるものが二変量であるときに一変量で信頼区間を書くと短くなってカバレッジが名目を下回るよ、ということにつながると思うので。
なお、上の論文では回帰式betaの信頼区間や信頼領域についても説明をしているのだけれど、私がこの記事で確認するのは、あくまで二変量正規分布のデータの分布に関する話。
1標準偏差や1.5標準偏差はどこから来たのか
自由度1のカイ二乗分布で68%をカバーする値は0.9889で、一変量で考えるとルートを取って0.9945。自由度2のカイ二乗分布で1がカバーする範囲は0.3934で約40%。二変量正規分布における40%領域が一変量での平均値±1標準偏差の区間となるということだと思う(この辺りの正確な?統計用語が分からなくなってしまったので雰囲気で書いている)。
> qchisq(0.68, df = 1)
[1] 0.9889465
> sqrt(qchisq(0.68, df = 1))
[1] 0.9944579
> pchisq(1, df = 2)
[1] 0.3934693
後々の描画ように取っておくために、自由度2のカイ二乗分布における40%と68%をカバーすることに対応する一変量正規分布の値を正確に出しておく。約1と1.5である。
> (multiplier_40 <- sqrt(qchisq(0.4, df = 2)))
[1] 1.010768
> (multiplier_68 <- sqrt(qchisq(0.68, df = 2)))
[1] 1.509592
ちなみに、みんな大好き95%だとどうかというと約2.5である。95%信頼区間を一変量として1.96で作っていると考えると結構な違い。
> sqrt(qchisq(0.95, df = 2))
[1] 2.447747
これらの数字を見るだけでも、複数関心のあるパラメタがあるときに人ずつ検定したらだめよということがより腑に落ちた気がする。また、P値だけ補正していても、信頼区間は結局補正できてないよね、という話も少し理解が進んだと思う。
理論値を描いてみる
これらの理解をより深めるべく、40%, 68%の二変量正規分布における理論値としての領域と、一変量に落とした場合の理論値としての区間が一致することを図示したい。上述の論文で相関係数が0.46の図を出していたので、まずはそれを真似てみる。
相関係数が0.46の時の結果。40%や68%の領域のrange()から作った区間と、平均値±sqrt(qchisq(0.4, df = 2))やsqrt(qchisq(0.68, df = 2))×標準偏差で作った区間を、楕円に接する形で並べた。数字でも完全に一致しているのだけれど(data not shown)、図でもきれいに一致した(理論値なので)。
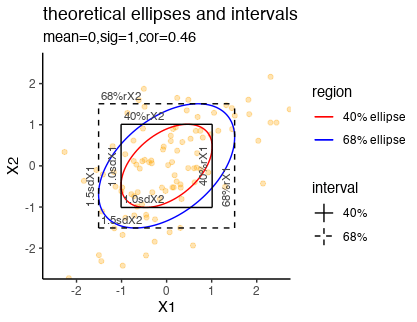
なんとなく、この一変量におけるカバレッジの悪さは、二変量の相関の大きさに依存する気がしたのだけれど、結果は変わらず。まぁ上で考えたカイ二乗分布の話には全く相関関係ないので、それはそうなのだけれど。
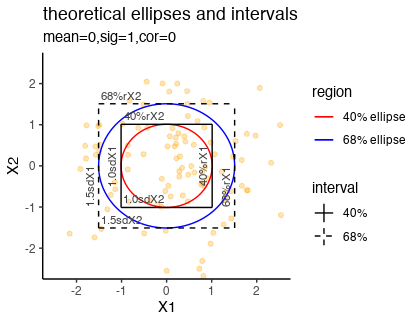
Rコード
楕円を書くコードはRで二変量確率分布の密度を可視化するときの注意というスクラップで作成したものと同じ。
library(tidyverse)
# Make my data
meanvec <- c(0,0)
covmat <- matrix(c(1, 0.46, 0.46, 1), nrow=2, byrow=T)
N <- 100
(mydata <- mvtnorm::rmvnorm(N, meanvec, covmat))
mydata <- data.frame(mydata)
# Function to generate ellipse points
generate_ellipse <- function(mean, covariance, level=0.95, n = 100) {
# Chi-squared critical value for 95% and 2 degrees of freedom
chi_sq_value <- qchisq(level, df = length(mean))
theta <- seq(0, 2 * pi, length.out = n)
circle <- cbind(cos(theta), sin(theta))
# sqrt(chi_sq_value) * circle produces
# the region of independent bivariate standard normal.
ellipse <- sqrt(chi_sq_value) * circle %*% chol(covariance)
ellipse + mean
}
# 40% ellipse
ellipse_points_40 <-
generate_ellipse(meanvec, covmat,
level = 0.4,
n = 500)
x1_40intv <- range(ellipse_points_40[,1])
x2_40intv <- range(ellipse_points_40[,2])
# 68% ellipse
ellipse_points_68 <-
generate_ellipse(meanvec, covmat,
level = 0.68,
n = 500)
x1_68intv <- range(ellipse_points_68[,1])
x2_68intv <- range(ellipse_points_68[,2])
label <- c("1.0sd", "1.5sd", "40%r", "68%r")
# Make mydata to be plotted
(
tmp <-
data.frame(
type = rep(label,each=2),
v = rep(c("X1","X2"),length(label)),
lwr = c(- multiplier_40 * sqrt(diag(covmat)),
- multiplier_68 * sqrt(diag(covmat)),
c(x1_40intv[1], x2_40intv[1]),
c(x1_68intv[1], x2_68intv[1])),
upr = c(multiplier_40 * sqrt(diag(covmat)),
multiplier_68 * sqrt(diag(covmat)),
c(x1_40intv[2], x2_40intv[2]),
c(x1_68intv[2], x2_68intv[2])),
coord1 = c(tmp$lwr[1],tmp$lwr[1],
tmp$lwr[3],tmp$lwr[3],
tmp$upr[1],tmp$upr[1],
tmp$upr[3],tmp$upr[3]),
coord2 = c(-1,-1,-1,-1,0,0,0,0),
coverage = c("40%","40%","68%","68%","40%","40%","68%","68%")
) %>%
rowwise() %>%
mutate(cat = paste0(type,v, collapse=",")) %>%
ungroup()
)
# Plot
ggplot() +
geom_point(data=mydata,
mapping=aes(X1,X2),
alpha=0.3,
col="orange") +
geom_path(data = as.data.frame(ellipse_points_40),
aes(V1, V2, col = "40% ellipse")) +
geom_path(data = as.data.frame(ellipse_points_68),
aes(V1, V2, col = "68% ellipse")) +
geom_linerange(data=subset(tmp,v=="X1"),
mapping=aes(
y=coord1,
xmin=lwr, xmax=upr,
linetype = coverage
)
) +
geom_linerange(data=subset(tmp,v=="X2"),
mapping=aes(
x=coord1,
ymin=lwr, ymax=upr,
linetype = coverage
)
) +
geom_text(data=subset(tmp,v=="X1"),
mapping=aes(x=coord1, y=lwr,label=cat
),
nudge_x = -0.2,
nudge_y = 1,
size = 3,
angle = 90,
col = "grey27") +
geom_text(data=subset(tmp,v=="X2"),
mapping=aes(y=coord1, x=lwr,label=cat
),
nudge_x = 0.5,
nudge_y = 0.2,
size = 3,
col = "grey27") +
scale_color_manual(name="region",
values=c("40% ellipse"="red",
"68% ellipse"="blue")
) +
scale_linetype_manual(name="interval",
values=c("40%"="solid",
"68%"="dashed")) +
coord_cartesian(xlim=c(-2.5,2.5), ylim=c(-2.5,2.5)) +
theme_classic() +
ggtitle("theoretical ellipses and intervals",
subtitle= paste0("mean=0,sig=1,cor=",covmat[2,1]))
参考
上述論文の著者のパッケージもあるみたい。
Discussion