Rで二変量確率分布の密度を可視化するときの注意
Rで二変量の同時分布の95%領域をいい感じに引きたい
と思って深く考えずに{ggdensity}をの関数を使っていて色々と混乱したので、まずその気づいていなかったことを整理する。
Rコードと結果
library(tidyverse)
# generate toy data -------------
set.seed(9998)
N <- 100
toy <-
mvtnorm::rmvnorm(n=N, mean = c(0,0),
sigma = matrix(c(1,0.3,0.3,1),
ncol = 2, byrow = T))
toy <- data.frame(toy)
# pre-calculation for marginal data intervals -------------------
mean_data <- colMeans(toy)
cov_data <- cov(toy)
tmp <-
data.frame(
x = rep(mean_data[1],2),
y = rep(mean_data[2],2),
lwr = mean_data - qnorm(0.975)*sqrt(diag(cov_data)),
upr = mean_data + qnorm(0.975)*sqrt(diag(cov_data))
)
# draw various 95% data regions ------------
# we can set the adjust parameter to apply a multiplicative adjustment
# to the heuristically determined bandwidth in method_kde()
# (which itself uses the one computed by MASS::bandwidth.nrd()):
ggplot() +
geom_point(data = toy,
mapping = aes(X1,X2), alpha = 0.2) +
geom_density_2d(data = toy,
mapping = aes(X1,X2,col = 'geom_density_2d')
) +
ggdensity::geom_hdr_lines(
data = toy,
mapping = aes(X1, X2, col="geom_hdr_lines, kde, adjust1"),
probs = 0.95, method = ggdensity::method_kde(
adjust = 1
),
alpha = 0.8
) +
ggdensity::geom_hdr_lines(
data = toy,
mapping = aes(X1, X2, col="geom_hdr_lines, kde, adjust2"),
probs = 0.95, method = ggdensity::method_kde(
adjust = 2 #smooth and close
),
alpha = 1
) +
ggdensity::geom_hdr_lines(
data = toy,
mapping = aes(X1, X2, col = "geom_hdr_lines, mvnorm"),
method = "mvnorm",
probs = c(0.95),
alpha = 1
) +
stat_ellipse(
data = toy,
mapping = aes(X1, X2, col = "stat_ellipse, norm"),
level = 0.95, type = "norm",
linetype = "dashed") +
stat_ellipse(
data = toy,
mapping = aes(X1, X2, col = "stat_ellipse, t"),
level = 0.95, type = "t") +
geom_linerange(data = tmp[1,],
mapping = aes(x = x, ymin = lwr, ymax = upr,
linetype = "marginal interval" )) +
geom_linerange(data = tmp[2,],
mapping = aes(y = y, xmin = lwr, xmax = upr,
linetype = "marginal interval")) +
geom_point(data = tmp[1,],
mapping = aes(x = x, y = y),
shape = 19,
col = 'white') +
scale_color_manual(name='95% data regions',
breaks=c("geom_hdr_lines, kde, adjust2",
"geom_hdr_lines, kde, adjust1",
'stat_ellipse, norm',
'geom_hdr_lines, mvnorm',
'stat_ellipse, t',
'geom_density_2d'),
values=c("geom_hdr_lines, kde, adjust1" = "grey",
"geom_hdr_lines, kde, adjust2" = "black",
'geom_hdr_lines, mvnorm'='red',
'stat_ellipse, norm'='blue',
'stat_ellipse, t'='green',
'geom_density_2d'='orange'
)) +
scale_linetype_manual(name = '95% data intervals',
breaks = c('marginal interval'),
values = c('solid')) +
theme_classic() +
ggtitle(paste0("MVN(0,sig=1,rho=0.3), N =",N))
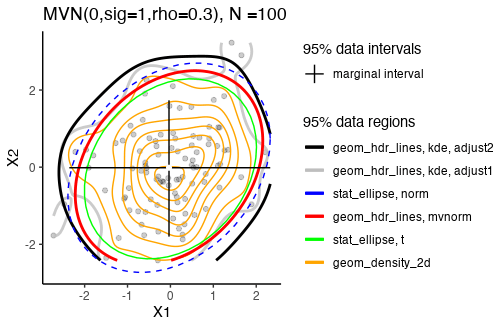
観察
- まず注意点として、データの95%の範囲を描画しているだけで、信頼区間ではない(stat_ellipseなどの説明がconfidence ellipseなどとされていることもあるが誤り)
- カーネル密度推定の滑らかさをadjust引数を使って上げていくと範囲は大きくなる。逆に小さいとbinを細かくしてデータにoverfitしてしまうので注意する。
- 多変量正規分布からサンプルを生成しているので、カーネル密度推定でもstat_ellipse(type="norm")やgeom_hdr_lines(method="mvnorm")に近い結果を出して欲しいが、N=100だとなかなか難しいのかもしれない。
- geom_hdr_lines(type="mvnorm")の方が、stat_ellipse(type="norm")よりも小さくなる傾向にある。
- seedを変えて何個か生成してみると、stat_ellipse()のデフォルトは多変量t分布で、多変量正規分布よりも領域が小さくなる傾向にある。
- seedを変えて何個か生成してみると、二変数あるうち片方を無視した範囲は領域よりも小さくなる傾向にある気がする。
- geom_density_2dはなんとなく使っただけでどういう方法で生成されているかは未確認。
今後やりたいこと
それぞれの方法が具体的にどういう仕組みなのかを調べて、可能ならばスクラッチで同じ結果を得たい。
謝辞
Triad sou.さんありがとうございました。
実施したこと
- 前回色々と描画したグラフのうち、
stat_ellipse(type=('norm'))による楕円を自分で再現してみる。 - データは前回と同じものを利用。
- コレスキー分解と固有値分解それぞれを使った方法を作成して目視で一致を確認した。
- 数値計算に疎すぎるのでよくわかっていないけれど、コレスキー分解の方が固有値分解よりも安定しているらしい。
-
chol()は上三角行列を出してくることに注意する。 - 行列の掛け算の順番を適切にするのにとても時間を要した。正直今も完全理解はできていない。
- カイ二乗分布を使う理由が、正規分布のexp()の中のマハラノビス距離がそれに従うからだが、計算の中では共分散行列の逆行列は使っていない。逆行列を使う方が数値誤差が出るらしい。
- 逆行列を取らなくても、どんな形の共分散行列でもいい感じに
AA^T
Rコードと結果
# Chi-squared critical value for 95% and 2 degrees of freedom
chi_sq_value <- qchisq(0.95, df = 2)
# Function to generate ellipse points using Cholesky decomposition
generate_ellipse <- function(mean, covariance, chi_sq_value, n = 100) {
theta <- seq(0, 2 * pi, length.out = n)
circle <- cbind(cos(theta), sin(theta))
# sqrt(chi_sq_value) * circle produces
# the 95% region of independent bivariate standard normal.
ellipse <- sqrt(chi_sq_value) * circle %*% chol(covariance)
ellipse + mean
}
# Generate ellipse points
ellipse_points <-
generate_ellipse(mean_data, cov_data,
chi_sq_value, n = 100)
# Function to generate ellipse points using eigen decomposition
generate_ellipse_eign <-
function(mean, covariance, chi_sq_value, n = 100){
theta <- seq(0, 2 * pi, length.out = n)
circle <- cbind(cos(theta), sin(theta))
covmat <- matrix(covariance, ncol=dim(covariance)[1], byrow=T)
eigenvalues <-eigen(covmat)$values
eigenvectors <-eigen(covmat)$vectors
eigenmat <- diag(sqrt(eigenvalues)) # Note: sqrt is used
# unit circle is extended to sqrt() to get standard deviation
ellipse <- t(eigenvectors %*% eigenmat %*% t(circle) * sqrt(chi_sq_value))
colnames(ellipse) <- attr(mean, "name")
ellipse + mean
}
ellipse_eigen_points <-
generate_ellipse_eign(mean_data, cov_data,
chi_sq_value, n = 100)
geomhdr_mvnorm_points <- reprecate_geomhdr_mvnorm(mean_data, cov_data, toy)
# Plot
ggplot(toy, aes(X1, X2)) +
geom_path(data = as.data.frame(ellipse_points),
aes(X1, X2, col = "ellipse_chor")) +
geom_path(data = as.data.frame(ellipse_eigen_points),
aes(X1, X2, col = "ellipse_eigen")) +
stat_ellipse(aes(X1, X2, col = "stat_ellipse, norm"),
type = "norm") +
stat_ellipse(aes(X1, X2, col = "stat_ellipse, t"),
type = "t") +
geom_point(alpha = 0.4) +
theme_classic() +
scale_color_manual(name='95% data region',
breaks=c("ellipse_chor",
"ellipse_eigen",
'stat_ellipse, norm',
'stat_ellipse, t'),
values=c("ellipse_chor" = 'black',
"ellipse_eigen" = "blue",
'stat_ellipse, norm' = 'red',
'stat_ellipse, t' = 'green'
)) +
ggtitle(paste0("MVN, sig=1,cov=0.3, N=",N))
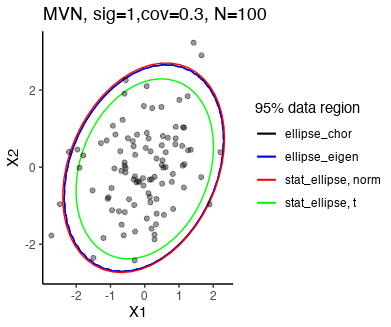
観察
- 多変量t分布の方は100個あるデータ点の中で10個以上が95%領域の外に位置しており、適切な領域サイズよりも狭くなっている。
番外編
- こちらの記事の固有値分解を図示したグラフを大体再現した。
mat <- 1/2*matrix(c(5,-3,-3,5), ncol=2, byrow=T)
eigenvalues <-eigen(mat)$values
eigenvectors <-eigen(mat)$vectors
eigenmat <- diag(eigenvalues)
d <-
data.frame(
type = "1.unit",
pick = as.factor(c(1,1,1, rep(0,n-3))),
circle) %>%
bind_rows(
data.frame(
type = "2.-eigenvec",
pick = as.factor(c(1,1,1,rep(0,n-3))),
t(-eigenvectors%*%t(circle))
)
) %>%
bind_rows(
data.frame(
type = "3.eignmat %*% -eigenvec",
pick = as.factor(c(1,1,1,rep(0,n-3))),
t(eigenmat%*%-eigenvectors%*%t(circle))
)
) %>%
bind_rows(
data.frame(
type = "4.eigen %*% eignmat %*% -eigenvec",
pick = as.factor(c(1,1,1,rep(0,n-3))),
t(eigenvectors%*%eigenmat%*%-eigenvectors%*%t(circle))
)
) %>%
bind_rows(
data.frame(
type = "5. eigen %*% sqrt(eign)",
pick = as.factor(c(1,1,1,rep(0,n-3))),
t(eigenvectors%*%sqrt(eigenmat)%*%t(circle))
)
) %>%
bind_rows(
data.frame(
type = "6. chol",
pick = as.factor(c(1,1,1,rep(0,n-3))),
circle %*% chol(mat)
)
)
# eigen() sorts eigen values in descending order
# therefore the graph does not coincide with that
# in the website.
ggplot() +
geom_point(data = d ,
mapping = aes(X1,X2, group = type,
col = pick),
show.legend = F) +
geom_path(data = d ,
mapping = aes(X1,X2, group = type,
col = pick),
show.legend = F) +
scale_color_manual(name = '',
values = c('0'='grey',
'1'='red'),
) +
facet_wrap(type~.) +
theme_classic()

観察
- 楕円を作成する際に掛けた、コレスキー分解と固有値ベクトル×sqrt(固有値)が、値は違うが等価になる理由が図示された。
-
eigen()は固有値を絶対値の大きい順にソートしてしまうので、微妙にあってはいない。
実施したこと
-
geom_hdr_lines(method = 'mvnorm')を自分で再現した。 - コードの中身はパッケージのページで紹介されていたので、自分で何か作ったわけではない。
- 使用されている
backsolve()を初めて使った。
Rコードと結果
# scratch - geom_hdr_lines(mvnorm) ------
reprecate_geomhdr_mvnorm <-
function(mean_data, cov_data,data) {
tmp <- backsolve(chol(cov_data), t(data) - mean_data, transpose = TRUE)
logretval <- -sum(log(diag(chol(cov_data)))) - log(2 * pi) - 0.5 * colSums(tmp^2)
exp(logretval)
}
# Create a grid
x1_range <- seq(min(toy$X1), max(toy$X2), length.out = 1000)
x2_range <- seq(min(toy$X2), max(toy$X2), length.out = 1000)
grid <- expand.grid(X1 = x1_range, X2 = x2_range)
# Compute density values
grid$density <- reprecate_geomhdr_mvnorm(mean_data, cov_data, grid)
grid <-
grid %>%
arrange(desc(density)) %>%
mutate(cumdens = cumsum(density)) %>%
mutate(r95 = ifelse(cumdens/max(cumdens) <= 0.95, T, F))
# Plot the region using ggplot2
ggplot() +
geom_point(data = toy,
mapping = aes(X1, X2)) +
geom_contour(data = grid,
mapping = aes(x = X1, y = X2,
z = density,
col='geom_contour(z=density)'
),
bins = 20 # the most outer ellipse is 95% line
) +
ggdensity::geom_hdr_lines(data = toy,
mapping = aes(X1, X2, col='geom_hdr_lines, mvnorm'),
method = 'mvnorm',
probs = 0.95,
show.legend = F,
alpha = 1) +
geom_raster(data = subset(grid, r95),
mapping = aes(x = X1, y = X2,
fill = '95% scratch'),
alpha = 0.5) +
scale_fill_manual(name = '',
values = c("grey")) +
scale_color_manual(name='',
values = c('geom_contour(z=density)'='blue',
'geom_hdr_lines, mvnorm'='black')
) +
theme_classic()
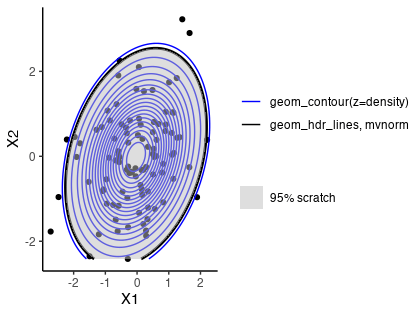
観察
- 再現は(当たり前だけど)バッチリできた。
-
geom_contourを使った方が若干広く、かつその方が、95%の領域としては正確なように見える。ここの原因はわかっていない。 - パッケージのページで紹介されていたコードは多変量正規分布にある、共分散行列の行列式が直接的には書かれていない。その部分を修正しても結果に影響はなかった。
- この部分については、上(下)三角行列の行列式が対角要素の積である性質を利用することで計算が速くて数値的に安定するそう。
- 具体的には、
|\Sigma| = \prod {diag(L)^2} -0.5 \cdot log((2 \pi )^k) - 0.5 \cdot log(\Pi {diag(L)^2)}) -0.5 \cdot 2 \cdot \sum log(diag(L)) = -\sum log(diag(L)) - また、パッケージの式には変数の数を表す
k k=2
- gridを1000×1000で作ったのでこのコードの実行速度は結構遅い。
geom_hdr_linesでgridをどのくらいにしているのか、そこの計算を高速化するための工夫があるのか、あたりのこともわかっていない。100×100だと、geom_rasterの描画する領域はまだカクカクと粗かった。
謝辞
Tomoki@UCLA Biostatisticsさん、行列式のところ教えていただきありがとうございました。
ggplot_build()でプロットの中身を確認したらgeom_contour()とgeom_hdr_lines()の違いの原因が分かるかも。
実施したこと
-
geom_density_2dの結果を再現した。 -
MASS::kde2dの中身をほぼそのまま使っている。tcrossprodやouterなど普段使わないbase関数があって勉強になった。 -
ggplot_build(p)でggplotで作図したグラフの裏側を見れることも今回初めて知れてよかった。
Rコードと結果
mygaussiankde2d <-
function(data, grid_n = 25, hx = 1, hy = 1) {
n <- nrow(data)
datax <- data[,1]
datay <- data[,2]
rangex <- range(datax)
rangey <- range(datay)
gridx <- seq(rangex[1],rangex[2], length.out = grid_n)
gridy <- seq(rangey[1],rangey[2], length.out = grid_n)
inputx <- outer(gridx, datax, '-')/hx
inputy <- outer(gridy, datay, '-')/hy
# cross products
dens <- tcrossprod(
matrix(dnorm(inputx), ncol = n),
matrix(dnorm(inputy), ncol = n)
)/(n*hx*hy)
# 後で数値確認をしやすくするように
# MASS::kde2dと同じリスト型の出力と
# ggplotを使いやすい縦型のdataframeの出力を行う
list(
dataframe =
data.frame(expand_grid(x = gridx, y = gridy)) %>%
bind_cols(
data.frame(z = dens) %>%
pivot_longer(cols = starts_with("z")) %>%
select(-name, z=value)
),
list = list(x=gridx, y=gridy, z=dens)
)
}
# MASS::kde2dはMASS::bandwidth.nrdをhに使うので
# 比較のために取得
bdw_x1 <- MASS::bandwidth.nrd(toy$X1)
bdw_x2 <- MASS::bandwidth.nrd(toy$X2)
# MASS::kde2dをみるとなぜかh <- h/4となっているので
# その調整を引数に入れている
dens <-
mygaussiankde2d(toy, grid_n = 50,
hx = bdw_x1/4, hy = bdw_x2/4)
p <-
ggplot() +
geom_point(data = toy,
mapping = aes(X1, X2)) +
geom_contour(data = dens$dataframe,
mapping = aes(x = x, y = y,
z = z,
col='mygaussiankde'
),
linetype = 'dashed',
linewidth = 1
) +
geom_density_2d(data = toy,
mapping = aes(X1, X2,
col='geom_density_2d'),
n = 50 # grid size
) +
scale_color_manual(name='',
values = c('mygaussiankde'='blue',
'geom_density_2d'='black')
) +
theme_classic()
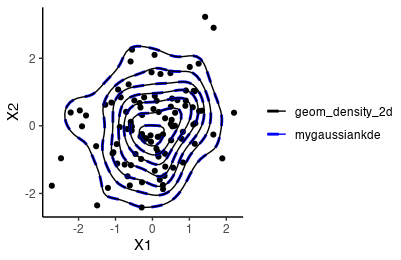
数値確認のコードは下記の通り。
k1 <-
MASS::kde2d(x=toy$X1, y=toy$X2, n = 50,
h=c(bdw_x1,bdw_x2))
k2 <-
MASS::kde2d(x=toy$X1, y=toy$X2, n = 50)
pdata1 <-
ggplot_build(p)$data[[2]] %>%
arrange(x,y,nlevel)
pdata2 <-
ggplot_build(p)$data[[3]] %>%
arrange(x,y,nlevel)
> all.equal(dens$list,k1)
[1] TRUE
> all.equal(k1,k2)
[1] TRUE
> all.equal(pdata1[,c('x','y','nlevel')],
+ pdata2[,c('x','y','nlevel')])
[1] TRUE
> pdata1 %>% count(nlevel)
nlevel n
1 0.1428571 167
2 0.2857143 125
3 0.4285714 103
4 0.5714286 91
5 0.7142857 71
6 0.8571429 51
7 1.0000000 27
> pdata2 %>% count(nlevel)
nlevel n
1 0.1428571 167
2 0.2857143 125
3 0.4285714 103
4 0.5714286 91
5 0.7142857 71
6 0.8571429 51
7 1.0000000 27
観察
-
MASS::kde2dの同時確率密度の計算方法は単純な二変量の確率密度の積になっている。相関を考慮していないように見えるが、相関の高い二変量正規分布でもそれなりにうまく推定できるぽいので結果的には考慮できていると考えればいいのかな。 -
geom_contourやgeom_density_2dのデフォルトのbinsは7になっているぽい?
実施したこと
-
geom_hdr_linesの再現に挑戦したが、微妙に再現し切れていない気がする。
Rコードと結果
# grid size of 100 produced a zigzag surface.
dens <-
mygaussiankde2d(toy, grid_n = 500,
hx = bdw_x1/4, hy = bdw_x2/4)
dens$dataframe <-
dens$dataframe %>%
arrange(desc(z)) %>%
mutate(cumdens = cumsum(z)) %>%
mutate(r95 = ifelse(cumdens/max(cumdens) <= 0.95,T, F)
)
ggplot() +
geom_point(data = toy,
mapping = aes(X1, X2),
alpha = 0.5) +
geom_raster(data = subset(dens$dataframe,r95),
mapping = aes(x = x, y = y,
fill='mygaussiankde'
),
alpha = 0.3
) +
ggdensity::geom_hdr_lines(data = toy,
mapping = aes(X1, X2),
# I noticed this lims arguments
xlim = c(-3, 3),
ylim = c(-3, 3),
probs = 0.95,
show.legend = T
) +
scale_fill_manual(name='',
values=c('mygaussiankde'='orange')) +
# the legend of geom_hdr_lines can be adjusted using alpha
scale_alpha_manual(name='',
values = 0.95,
labels=c('geom_hdr_lines')) +
# eliminate the line symbol in the legend for geom_raster
guides(fill = guide_legend(override.aes = list(linetype = 0))) +
theme_classic() +
theme(legend.margin = margin(0, 0, 0, 0),
# reduce the margin between two symbols produced
# by different aesthetics
legend.spacing.y = unit(0, 'cm')) +
ggtitle('default h param')
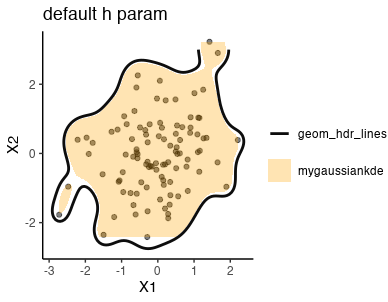
観察
- 微妙に自分の関数だと色をぬれていない領域がある。
今後やりたいこと
-
geom_hdr_linesの中身を調べる。
kdeのグリッドの範囲をデータの最大最小よりも少し広く取ったら行けそう。たぶんhを大きくするとグリッドもその分広がってないといけない。→下の記事で対応済み。
実施したこと
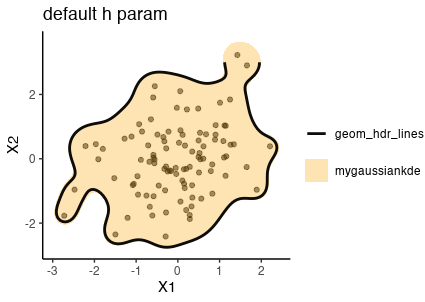
- 前回
geom_hdr_linesを再現できなかったのはgridの端が実データの存在する領域に限られていたからではないか、と考えて関数を修正したところうまく再現に成功した。
Rコードと結果
- 修正したガウシアンKDEの関数のみ記載する。
mygaussiankde2d_v2 <-
function(data, grid_n = 25, hx = 1, hy = 1) {
n <- nrow(data)
datax <- data[,1]
datay <- data[,2]
rangex <- range(datax)
rangey <- range(datay)
# In the coming example,
# we know that the two variables are continuous
# so just arbitrarily multiply with 1.3
gridx <- seq(rangex[1]*1.3,rangex[2]*1.3, length.out = grid_n)
gridy <- seq(rangey[1]*1.3,rangey[2]*1.3, length.out = grid_n)
inputx <- outer(gridx, datax, '-')/hx
inputy <- outer(gridy, datay, '-')/hy
# cross products
dens <- tcrossprod(
matrix(dnorm(inputx), ncol = n),
matrix(dnorm(inputy), ncol = n)
)/(n*hx*hy)
list(
dataframe =
data.frame(expand_grid(x = gridx, y = gridy)) %>%
bind_cols(
data.frame(z = dens) %>%
pivot_longer(cols = starts_with("z")) %>%
select(-name, z=value)
),
list = list(x=gridx, y=gridy, z=dens)
)
}
実施したこと
-
geom_hdr_lines(method = ggdensity::method_kde(adjust = 2))を完全にではないがおおよそ再現できた。
Rコードと結果
- ガウシアンKDEの計算において、
adjust=2は元々のhへの入力に2を掛けることで反映した。
bdw_x1 <- MASS::bandwidth.nrd(toy$X1)
bdw_x2 <- MASS::bandwidth.nrd(toy$X2)
dens <-
mygaussiankde2d_v2(toy, grid_n = 500,
hx = bdw_x1*2/4, hy = bdw_x2*2/4)
- 95% HDRの計算方法は変わらないので割愛。
-
geom_hdr_linesでhをadjust引数を使って調整して描画する。 -
geom_tile()に変更されているのはそうせよというワーニングが出たからで深い理解は特にない。
ggplot() +
geom_point(data = toy,
mapping = aes(X1, X2),
alpha = 0.5) +
geom_tile(data = subset(dens$dataframe,r95),
mapping = aes(x = x, y = y,
fill='mygaussiankde'
),
alpha = 0.3
) +
ggdensity::geom_hdr_lines(data = toy,
mapping = aes(X1, X2),
xlim = c(-3, 3),
ylim = c(-3, 3),
probs = 0.95,
show.legend = T,
method = ggdensity::method_kde(
adjust = 2)
) +
scale_fill_manual(name='',
values=c('mygaussiankde'='orange')) +
scale_alpha_manual(name='',
values = 0.95,
labels=c('geom_hdr_lines')) +
guides(fill = guide_legend(override.aes = list(linetype = 0))) +
theme_classic() +
theme(legend.margin = margin(0, 0, 0, 0),
legend.spacing.y = unit(0, 'cm')) +
ggtitle('adjust=2; lims(-3,3)')
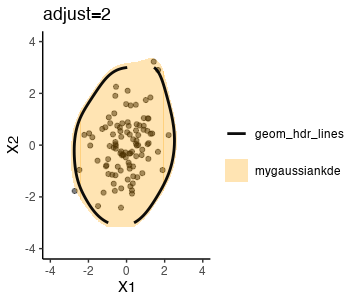
-
xlimとylimを少し広げて全体を見ようとしたところ、これはggplot2::lims()と同じ挙動をしているようで、KDEの出力範囲が実データ範囲を超えていることとgeom_hdr_linesで計算している範囲がおそらく違うことによって、描画結果が変わってしまった。下図が(-4,4)の範囲に変更したもの。
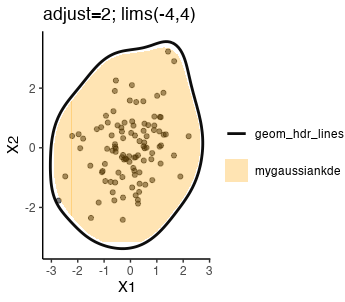
観察
- 完全な一致には至らなかったが、大体一致はしているので大まかな仕組みはこの理解で良いと考えられる。
実施したこと
stat_ellipse(type='t)で何が起こっているのかを眺める。結果、t分布を使うくらいならKDEを使えばいいかなという気がしている。
内容
stat_ellipse(type='t)のソースコードを見てみると、MASS::cov.trobを使ってロバストな共分散行列を推定しているらしい。その後はコレスキー分解をしておりやっていることは正規分布の楕円を推定する時と同じ模様。
当該関数の中身はこんな感じということで貼り付けておく。この共分散行列がかなり小さく計算されることがstat_ellipse(type='norm')と比べて領域が小さく出ることの要因と思われる。
> MASS::cov.trob
function (x, wt = rep(1, n), cor = FALSE, center = TRUE, nu = 5,
maxit = 25, tol = 0.01)
{
test.values <- function(x) {
if (any(is.na(x)) || any(is.infinite(x)))
stop("missing or infinite values in 'x'")
}
scale.simp <- function(x, center, n, p) x - rep(center, rep(n,
p))
x <- as.matrix(x)
n <- nrow(x)
p <- ncol(x)
dn <- colnames(x)
test.values(x)
if (!(miss.wt <- missing(wt))) {
wt0 <- wt
test.values(wt)
if (length(wt) != n)
stop("length of 'wt' must equal number of observations")
if (any(wt < 0))
stop("negative weights not allowed")
if (!sum(wt))
stop("no positive weights")
x <- x[wt > 0, , drop = FALSE]
wt <- wt[wt > 0]
n <- nrow(x)
}
loc <- colSums(wt * x)/sum(wt)
if (is.numeric(center)) {
if (length(center) != p)
stop("'center' is not the right length")
loc <- center
}
else if (is.logical(center) && !center)
loc <- rep(0, p)
use.loc <- is.logical(center) && center
w <- wt * (1 + p/nu)
endit <- 0
for (iter in 1L:maxit) {
w0 <- w
X <- scale.simp(x, loc, n, p)
sX <- svd(sqrt(w/sum(w)) * X, nu = 0)
wX <- X %*% sX$v %*% diag(1/sX$d, , p)
Q <- drop(wX^2 %*% rep(1, p))
w <- (wt * (nu + p))/(nu + Q)
if (use.loc)
loc <- colSums(w * x)/sum(w)
if (all(abs(w - w0) < tol))
break
endit <- iter
}
if (endit == maxit || abs(mean(w) - mean(wt)) > tol || abs(mean(w *
Q)/p - 1) > tol)
warning("Probable convergence failure")
cov <- crossprod(sqrt(w) * X)/sum(wt)
if (length(dn)) {
dimnames(cov) <- list(dn, dn)
names(loc) <- dn
}
if (miss.wt)
ans <- list(cov = cov, center = loc, n.obs = n)
else ans <- list(cov = cov, center = loc, wt = wt0, n.obs = n)
if (cor) {
sd <- sqrt(diag(cov))
cor <- (cov/sd)/rep(sd, rep.int(p, p))
if (length(dn))
dimnames(cor) <- list(dn, dn)
ans <- c(ans, list(cor = cor))
}
ans$call <- match.call()
ans$iter <- endit
ans
}
個人的にやっぱり謎なのは、t分布の方が裾が重い分布のはずなので正規分布を仮定したときよりも領域は広く推定されそうなのにそうならないことである。で、関数を眺めていた中で自由度を表すnuがデフォルトで5に設定されていることが気にはなった。実際、この値を変えると結構推定値が変わる。
N <- 100
toy <-
mvtnorm::rmvnorm(n=N, mean = c(0,0),
sigma = matrix(c(1,0.3,0.3,1),
ncol = 2, byrow = T))
toy <- data.frame(toy)
> (cov_data_norm <- cov(toy))
X1 X2
X1 0.9234213 0.3749573
X2 0.3749573 1.0981653
>
> for(i in 1:10) {
+ print(paste0('nu=',i))
+ print(MASS::cov.trob(toy, nu = i)$cov)
+ }
[1] "nu=1"
X1 X2
X1 0.4338750 0.1688706
X2 0.1688706 0.4944212
[1] "nu=2"
X1 X2
X1 0.5354083 0.2078658
X2 0.2078658 0.6259194
[1] "nu=3"
X1 X2
X1 0.5957586 0.2315329
X2 0.2315329 0.7050505
[1] "nu=4"
X1 X2
X1 0.6386245 0.2488490
X2 0.2488490 0.7608612
[1] "nu=5"
X1 X2
X1 0.6700584 0.2617504
X2 0.2617504 0.8011481
[1] "nu=6"
X1 X2
X1 0.6948066 0.2720812
X2 0.2720812 0.8323834
[1] "nu=7"
X1 X2
X1 0.7148898 0.2805811
X2 0.2805811 0.8573667
[1] "nu=8"
X1 X2
X1 0.7315549 0.2877158
X2 0.2877158 0.8778310
[1] "nu=9"
X1 X2
X1 0.7465017 0.2942250
X2 0.2942250 0.8959227
[1] "nu=10"
X1 X2
X1 0.7583779 0.2993947
X2 0.2993947 0.9101950
>
ChatGPTにコードを解説してもらいながら考えたのだけれど、nuが小さいほど、重みwを更新する式でマハラノビス距離Qの影響が大きくなるので、この距離に影響する外れ値の影響を受けて重みが変化する。なので、外れ値が多いときにはnuを小さくするのがいいらしい。元のデータが正規分布でしかもサンプルデータではN=100あるので、外れ値はあまりなさそうということを考えると、nu=5というデフォルトの値は小さすぎるのではないか?という気がする。
(自分でシミュレートすればいいのだが)ググって見つけたこちらの文献を見ると自由度10だと目で見る限りはほぼ正規分布出だ、自由度5もまぁそこまで違わないように見えるけど、その多少の違いが大きく影響していたという感じだろうか。
なお、ここでいう自由度は「サンプルサイズ−パラメタ数」とは違いチューニングパラメタ的な感じらしい。by ChatGPT
ググっていたら、色々なヘビーテイル分布の共分散行列推定の比較と新しいパッケージのVignetteが見つかった。沼である。