Bayesian Analysis with PyMC 勉強ノート 1~3

追記: 内容をすこし正確にして、標準ベイズ統計学風の進め方で書き直しました。

https://zenn.dev/inaturam/articles/3c39f2abd05c72

---

Osvaldo Martin 著 金子 武久 訳
Pythonによるベイズ統計モデリング
2018-06-26
https://www.kyoritsu-pub.co.jp/book/b10003944.html

Pythonによるベイズ統計モデリング(PyMCでのデータ分析実践ガイド)を読んだので学習メモを残します。学習中のノートなので正確ではない表記がいくつかあります。また、使われているコードをPyMC3からPyMC5に書き直しました。

https://www.kyoritsu-pub.co.jp/book/b10003944.html

確率的に考える

次のライブラリを使用する。

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import seaborn as sns

1. モデリング方式としての統計学

実験計画(experimental desige): データ収集を扱う統計学では、扱う問題は何か・使うべき方法は何かを考えてからデータを収集するその方法を研究する。

探索的データ分析(explortory data analysis; EDA): データが集まったあと、それを調べたり可視化したりする。

• 記述統計学: 数量的にデータを要約したり特徴づけたりする。 ← 平均や分散など
• データ可視化: データを視覚的に調べる。 ← ヒストグラムや散布図など

推測統計学(inferential statistics): データに基づいた一般化や予測を司るため、確率モデルを使う。

モデル: 与えられたシステムや過程の記述を簡潔にするもの。すべての特徴を考慮することを意図しているわけではない。 → 単純なモデル・複雑なモデル

ヒューリスティック(発見的方法): 正確な答えを導く訳では無いがおおよそうまくいく方法

ベイジアンモデリングでは3つのステップでモデルを構築する。

1. データが生成された過程の仮定をおいて、所与のデータに対して大雑把な近似を目指す
2. ベイズの定理からモデルにデータを与えて、仮定と結合させる(データに基づいてモデルを条件付ける)
3. データやテーマに関して専門的な基準からモデルの妥当性をチェックする

2. 確率と不確実性

ベイジアンの観点からは、現象に仮定を与えることで不確実性を減らす。
例えばコインの裏表に関して無情報であれば不確実性は最大で、確率は0~1任意の値になり得る。逆にコインが均一であると確信しているるなら確率は0.5になるだろうと予想がつく。

→ データに対してこの仮定を更新することで、現象の不確実さを減らすことができる。ベイジアンではこの不確実性の数量化を確率として行う。

Cromwell Rule: 論理的に真か偽である言明に対して事前確率は1か0かを予約する。

→ Coxは不確実性があるとき、このルールを確率を用いて拡張できることを証明した。これはベイジアンの方法に合致している。

同時確率(joint probability): $p(A,B)$

条件付き確率(conditional probability): $p(A|B)$ ← 事象Aの確率がBによって条件付けられている様子。AとBが独立ならば同時確率に等しい。則ち、条件付き確率はそれらの同時確率より大きい

乗法定理: $p(A,B) = p(A|B)p(B)$ ← 同時確率$P(A,B)$は、Bが与えられたもとでAが起こる確率$P(A|B)$と、Bがおこる確率$P(B)$の積

この時、同時分布を再帰的に展開したものがベイズの定理。

$$p(A|B) = \frac{p(A,B)}{P(B)} \\ = \frac{p(B|A)p(A)}{p(B)}$$

なぜ$p(B)$で割っている? ← Bを知ること == 事象空間をBに制限すること。則ち、条件付けられた該当例を数え上げ、それを該当事象の総数で割れば良い。

確率分布

一般的には、データは未知のパラメータを持った分布から生起していると考える。
パラメータは観測されずデータだけが世界から与えられるので、ベイズの定理を用いてデータからパラメータを求める。

ガウス分布(normal distriburtion)

$$N(x|μ,σ) = \frac{1}{σ\sqrt{2π}} e^{-\frac{(x-μ)^2}{2σ^2}}$$

$μ$: 平均(median) = 最頻値(mode)に一致
$σ$: 標準偏差

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import seaborn as sns

x = np.linspace(-5,5,100)
mu = 0
sd = 1

dist = stats.norm(mu, sd)
y = dist.pdf(x)

plt.plot(x,y)

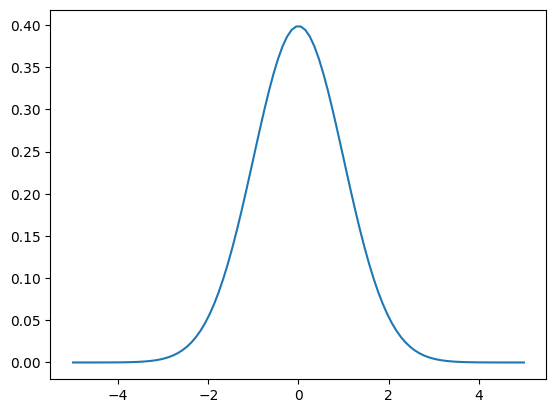
確率変数(random variable): 確率分布に由来する変数$x$は任意の値を取ることはできず、確率分布に制約を受けてる。$x ~ N(x|μ, σ)$のように記述される。

ベイズの定理と統計的推測

• $D$: データ
• $H$: 仮説

$$p(H|D) = \frac{p(D|H)p(H)}{p(D)} \\ ∝ p(D|H)P(H)$$

このベイズの定理において、項は以下の呼び方をする。

• $p(H)$ 事前分布(prior): データを知る前のパラメータの値について、知っていることを反映する分布
• $p(D|H)$ 尤度(likelihood): 仮説の分布とそのパラメータがどれだけデータにフィットしているかを示す値
• $p(H|D)$ 事後分布(posterior): データを知ったあとそれを反映した分布
• $p(D)$ 周辺尤度(mrginal likelihood) 。パラメータが取りうるすべての値について平均化した値。定数の正規化項。エビデンス(evidence)とも

3. 単一パラメータ推論

コインの裏表問題は相互に排他的な2値変数からなり、このような2値問題はあらゆる場面で直面する。データはすでに取り終わっていてDが既知であることとする。

コインの偏りとして、0,1は常に裏,表が出ていて、0.5は半々なことを意味する。

偏りを表すパラメータθ、コインで表が出た場合を表す変数yとすると、$p(θ|y) ∝ p(y|θ)P(θ)$となる。この設定でモデリングを行う。

1. 尤度の選択をする。今回は表か裏がが排他的に出現するため、母数θのもとでN回のうち表がy回でる確率を返す離散確率分布、つまり二項分布(binomial) を尤度として使うとする。直感的にはθはコインを投げた時の表が出る確率を、その現象が(N-y)回起こったと表す。

$$p(y|θ) = \frac{N!}{(y!(N-y)!)} θ^y (1-θ)^{N-y}$$

pdf(probability density function): 確率密度関数
pmf(probability mass function): 確率質量関数(離散確率分布)

n = 5
p = 0.5  # コインが表を出すと思われる確率の仮説
x = np.arange(0, 10)

dist = stats.binom(n=n, p=p)
y = dist.pmf(x)

plt.plot(x, y, marker="o", ls="")

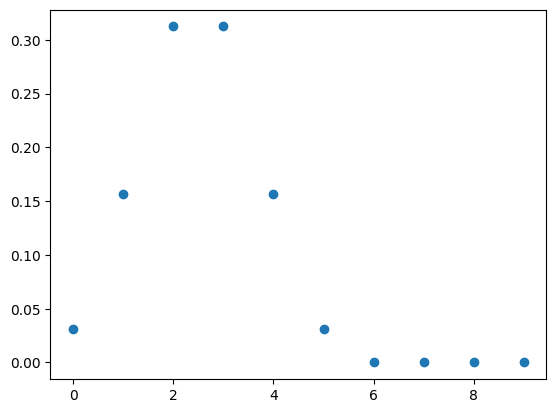
2. 事前分布を選択する。基本的には尤度の共役事前分布を使用することで、計算を抑えて事後分布として事前分布と同じ族の分布を得られるようにする。

今回は二項分布の共役事前分布であるbeta分布 を用いる。$Γ$はガンマ関数、$α,β$は分布を制御するパラメータ。beta分布はパラメータによって凸にも凹にもなる柔軟な分布で、二項分布と同じく閉区間[0,1]に制限される。
(ただし、現代的なサンプリングなどを使えば共役でなくても解析的に分布を表すことができるため、共役事前分布は必須ではない。)

$$p(θ) = Beta(α,β) \\ = \frac{Γ(α+β)}{Γ(α)Γ(β)} θ^{α-1} (1-θ)^{β-1}$$

a = 10
b = 2
x = np.linspace(0, 1, 100)

dist = stats.beta(a,b)
y = dist.pdf(x)

plt.plot(x,y)

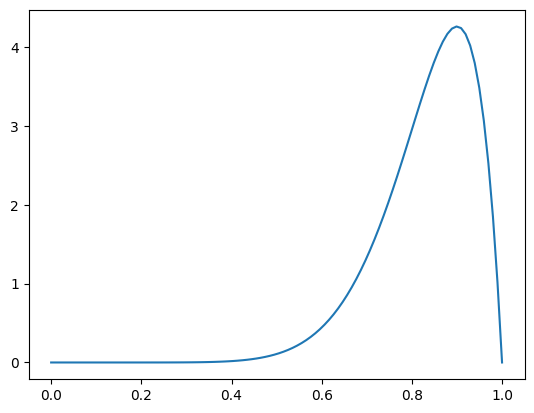
3. 事後分布を計算する。ベイズの定理により、今回設定した尤度と事前分布の積を計算することで事後分布になる。

ここは尤度に対して共役事前分布を用いたことで、事後分布もまた事前分布とおなじ族の確率分布になっていることがわかる。

$$p(θ|y) ∝ Beta(α+y, β+N-y) \\ = θ^{α-1+y} * (1-θ)^{β-1+N-y}$$

theta_real = 0.5

N = 16  # traial
y = 4  # data

a_prior = 3
b_prior = 3

x = np.linspace(0, 1, 100)

dist = stats.beta(a_prior + y, b_prior + N - y)
posterior = dist.pdf(x)

plt.plot(x, posterior)

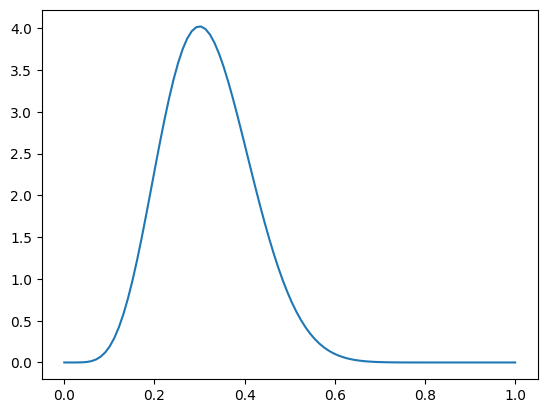
• trial = 0 のとき、事後分布のパラメータは事前分布のままである。
• beat分布のパラメータを(1,1)とした場合 → 事前分布を一様分布としたことになり、[0,1]で全体的に平たくなり、試行回数が小さいと全体的に偏りが生まれないが、試行回数が大きくなるごとに真のθに近づいていく。
• beat分布のパラメータを(10,10)とした場合 → 事前分布が0正規分布ににた分布としたことになり、0.5に集中した分布になる。試行回数が小さいと殆ど動かないが、大きくなるごとに真のθに近づいていく。

特に(10,10)などのとき、事前分布はコインは公正であるという信念 と両立する。
この信念ということばはベイジアンではよく使われるが、「データによって情報が与えられるモデル」というほうが正しい。

• 最もありえる値は事前分布の最頻値として与えられる。
• 事前分布の広がりはパラメータの不確実性の大きさに比例する。
• (試行回数/データ数)が同じでも、データが大きいほど信念を支持してくれて不確実性(広がり)が小さくなる。
• データ数が無限の極限ですべての事前分布は同じ事後分布に収束する。
• 事後分布の収束はデータとモデルに依存する。

事後分布が推論結果に影響してしまうことを恐れてしまうビギナーベイジアンは可能な限り無情報の分布を使いたがるが、データが語ることは限りがあることを思えば、事前分布に信念を語らせることは概ね良いことである。

パラメータの値域や近似的な範囲などわかることを正則化事前分布 として与えることで、事後分布の値域を制限できることができる。

ある意味、頻度論 は一様事前分布などのベイジアンモデルの特殊版とも言えるが、ベイジアンの確率分布推定は点推定量として母数を特定するよりも透明性があり、批評やデバッグが可能な点で優れている。

4. ベイジアン分析の情報伝達

2値問題におけるベイズ推論の結果を解釈して要約したり記録したりできる。$θ ~ Beta(α,β)$, $y ~ Bin(θ)$のとき、以下の方法で記述することができる。

Kruschkeのダイアグラム: 上段にθを生成する事前分布とそのパラメータα,βを書き、その下に矢印をかいて尤度とデータ数n、その下にデータyを書き入れる。発展的にはベイジアングラフィカルモデルを用いることがある。

事後分布の要約

最高事後密度(hidhest posterior density; HPD): ベイズ的な信用区間(credible interbal) を意味する。95%HPDはよく使われる。

これはパラメータの真の値が固定値であり区間を真値の含むか含まないかの割合であるという仮定を持つ頻度主義の信頼区間(confidence interbal) とは異なり、95%HPDは95%の確率でそこに存在すると解釈できる。これは頻度論より直感的である。また何%を用いるかはデータ解析での文脈を考慮して決める必要がある。

単峰性の分布では両側計算するだけでよいが、多峰性の分布では山の区間に分けないといけないので処理が面倒である点に注意。

def naive_95hpd(post):
    sns.kdeplot(post)
    hpd = np.percentile(post, [2.5, 100-2.5])
    return plt.plot(hpd, [0,0], linewidth=20)

post = stats.beta.rvs(5, 11, size=100)
naive_95hpd(post)

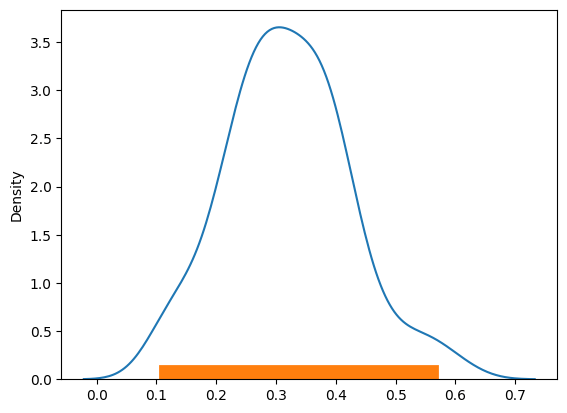
自己一貫性: 観測値と予測データの差に焦点を当てて分析するとき、これらの分布が似ていない場合はモデリングやデータを与える際になにか問題が発生しているか、改善の余地がある。どの程度の精度が欲しいかによってこれを制御することが良い。

確率プログラミング

次のライブラリを使用する。

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import pymc as pm
import arviz as az 

PyMCによりベイズモデリングを行う。

ベイズ統計ではデータは所与の変えられないものとして扱い、それに関わるパラメータの尤もらしいものを求める。すべての未知のパラメータは確率分布で扱われ、これを尤度の設計と事前分布の設定により事後分布を推論する。これは一種の学習である。

ここで出てくる周辺尤度は複雑な積分を含んでおり、数値的解析で解く必要が出てくるが、これを計算機のパワーでなんとかして、推論ボタン1つで解けるようにしたのがPyMCである。

事後分布が解析的に溶けない場合でも、それを計算する方法は以下のように存在する。

1. 確率プログラミング

• 非マルコフ的方法(グリッドコンピューティング, 2次近似, 変分法)
• マルコフ的方法(メトロポリスヘイスティング, ハミルトニアンモンテカルロ, No Uターンサンプラー)

特に変分法とマルコフ連鎖モンテカルロ(MCMC) はよく使われる。

グリッドコンピューティング

力ずくで計算する。事後分布全体が計算できなくても、与えられた点に対して事前分布と尤度を計算できる。パラメータ間に区間を定義してそのなかにグリッド点を与え、各点に対して尤度と事前分布を計算する。この結果を全体で割ることで正規化する。

グリッドアプローチでは複数のパラメータには尺度付けできず、事後分布の規模はサンプリングされた規模と相対的に小さくなる、 → あまり意味のない計算に時間を費やすことになる。

def gridcom(gridpoint, head, toss):
    grid = np.linspace(0, 1, gridpoint)
    prior = np.repeat(5, gridpoint)
    likelihood = stats.binom.pmf(head, toss, grid)
    
    posterior_unstd = likelihood * prior
    posterior = posterior_unstd / np.sum(posterior_unstd)

    return grid, posterior

point = 15
h = 3  # 表の回数
n = 4  # 試行回数

grid, posterior = gridcom(point, h, n)
plt.plot(grid, posterior)

2次的方法

ラプラス法(Laplace method) などで正規分布の事後確率を近似する。
事後分布の最頻値をみつけて最適化(最小最大の探索)をおこなうことで計算する。
事後分布は最頻値近傍で正規分布に似るためこれが使える。
この最頻値近くにおける曲率を推定することで正規分布に類似した分布の偏差を得ることができる。

変分法

データが大きすぎたり計算があまりに困難な尤度を用いるとき、マルコフ的な方法では遅すぎるような場合に使用する。MCMCの初期値としてこれを用いることは事後分布を高速に近似できるようになるため効率が良い。

モデルに対して独自のアルゴリズムを用いなければならない点が欠点で、これを一般化する試みが多くされている分野。

自動微分変分推論(ADVI): 推定したいパラメータを対数変換などで区間[-∞,∞]に飛ばし、ガウス分布を用いて近似する。このガウス分布は変換前のパラメータの空間ではガウス分布ではないことに注意。周辺尤度の下限を最大化 == 真の事後分布とのKLダイバージェンスを最小化することを目的として最適化する。PyMCでも使える。

マルコフモンテカルロ法(MCMC)

グリッドコンピューティングよりよい方法で、確率の高いところにとどまってサンプリングすることで効率化する。たとえば領域AがBよりも2倍の確率を持つならAではBの2倍サンプル抽出を行うという雰囲気の方法で、これにより解析的にすべての事後分布が計算できなくてもサンプリングサイズを大きくすることで正確に算出できる。

モンテカルロ法: サンプリングによって解析的に面積を求める。

N = 15000  # サンプル数
x, y = np.random.uniform(-1,1, size=(2,N))  # 半径1の正方形内をサンプリング

inside = (x**2 + y**2) <= 1  # 円内の数を数える
outside = np.invert(inside)

pi_pred = np.sum(inside) * 4/N  # 円周率を面積公式 S = R^2 * π から求める 
pi_true = np.pi
print(f"{pi_pred=}")
print(f"{pi_true=}")

plt.plot(x[outside], y[outside], "r")
plt.plot(x[inside], y[inside], "b")
plt.show()

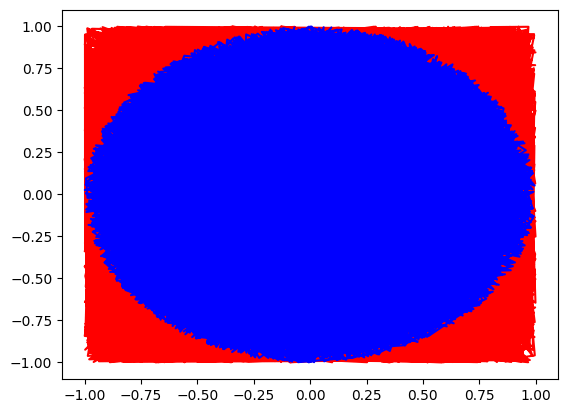
マルコフ連鎖(Markov chain): t-1の状態からのみtの状態が決まる(他の状態とは独立な)確率遷移モデルを使う。
サンプリングしたい分布(事後分布)に比例する遷移を持ったモデルを見つけることができるならばその過程を用いてサンプリングする。事後分布がわからないときは詳細つり合い条件(detailed balance condition) より逆過程が順過程と等しい確率であると仮定して、これを満たすマルコフ連鎖からサンプリングできればよい。

メトロポリスヘイスティングス(metropolis hastings algorithm)

詳細つり合いを満たすサンプリングアルゴリズム。任意の分布から確率$p(x)$でサンプリングできる。ベイズの計算で最も大変な周辺尤度はこれにより計算可能となる。

1. パラメータ$x_i$の初期値を決める
2. 新しいパラメータ$x_{i+1}$を、サンプリングが簡単な提案分布(prpposal distribution) $q(x_{i+1}|x_i)$から求める。これは$x_i$を撹乱している操作として解釈できる
3. メトロポリスヘイスティング基準を用いて新しいパラメータを棄却するかどうか計算する
4. 十分なサンプルチェーン(サンプルトレース) が取れるまで繰り返す

次の基準を用いる。

$$p(x_{i+1}|x_i) = min(1, \frac{p(x_{i+1})q(x_i|x_{i+1})}{p(x_i)q(x_{i+1}|x_i)} )$$

特に分布qは対象性をもつ場合、メトロポリス基準が成り立つ。

$$p(x_{i+1}|x_i) = min(1, \frac{p(x_{i+1})}{p(x_i)} )$$

これにより積分値をサンプルの数値列で置き換えることができる。
MCMCは汎用的なアルゴリズムで、非ベイジアンな分子モデルでは分布のxの値は系におけるエネルギーとして読み替えることができる。

def metropolis(func, step):
    samples = np.zeros(step)
    old_x = func.mean()
    old_pred = func.pdf(old_x)

    for i in range(step):
        new_x = old_x + np.random.normal(0, 0.5)
        new_pred = func.pdf(new_x)
        acceptance = new_pred/old_pred

        if acceptance >= np.random.random():
            samples[i] = new_x
            old_x, old_pred = new_x, new_pred
        else:
            samples[i] = old_x
    return samples

f = stats.beta(10,5)
samples = metropolis(f, 5000)

x = np.linspace(0.01, 0.99, 100)
y = f.pdf(x)  # 真の分布

plt.plot(x, y, lw=3)
plt.hist(samples, bins=30, density=True)
plt.show()

ハミルトニアンモンテカルロ

サンプリングの時間を短縮できる効率的なアルゴリズムを統計力学の観点から設計した方法。
系における全エネルギー(ハミルトニアン)をもちいて、メトロポリスヘイスティングではランダムに動かしていた確率遷移を勾配に沿った方向へ動かすことで、計算コストは増えるが良い結果を得られる。
この改良版であるNo Uターンサンプラー はPyMCで用いられ、詳細な調整なしに良い結果を得られる。
この他にも分子シュミレーションの観点からレプリカ交換法やメトロポリス結合MCMCなどがある。

2. コイン投げ問題の計算的アプローチ

まずモデルの記述を行い、推論ボタンを押すだけ。

$$θ \sim Beta(α,β) \\ y \sim Bin(n=1, p=θ)$$

$\text{Bin}(n=1, p=θ)$: n=1の2項分布、つまりベルヌーイ分布のこと。

n_experiments = 8
theta_real = 0.3
data = stats.bernoulli.rvs(p=theta_real, size=n_experiments)

with pm.Model() as first_model:
    theta = pm.Beta("theta", alpha=1, beta=1)
    y = pm.Bernoulli("y", p=theta, observed=data)

    # 事後確率最大化をメトロポリスヘイスティングでおこなう
    start = pm.find_MAP()
    step = pm.Metropolis()
    trace = pm.sample(1000, step=step, initvals=start)

# 結果の確認
# 良い性能を得るにはバーンインと呼ばれる初期のサンプルを捨てる手法を使う (trace[100:] など)
chain = trace

az.plot_trace(chain, lines={"theta": theta_real})

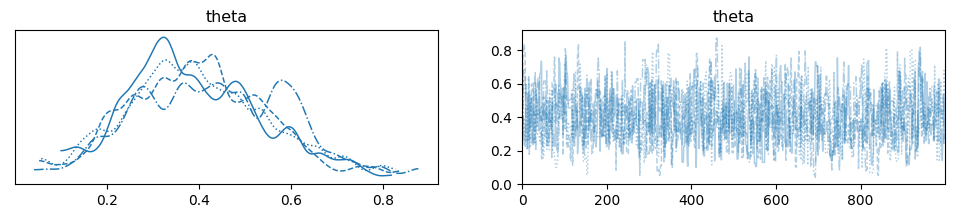
ここでplot_traceで表されるグラフはKDEとチェインの値。θの推定値はデータ数が増えると正規分布に近づく。
チェーンは推定値付近でフラクタルに摂動していると望ましいが、最初の付近でフラクタルが崩れていたり(バーンインで削るべき)、全体的に変な偏りが発生していたら良くない状態。

pm.sample()にcores引数を追加することで、並列でn個のチェーンを推論できる。

with first_model:
    step = pm.Metropolis()
    trace_m = pm.sample(1000, step=step, cores=4)  # njpbsはcoresになった

chain_m = trace_m

az.plot_trace(chain_m, lines={"theta": theta_real})

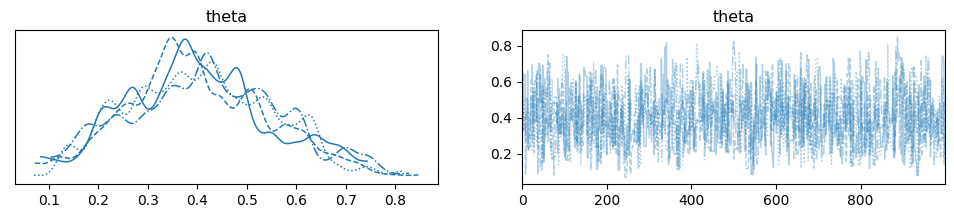
数量的に収束性をチェックするにはGelman-Rubinテスト を行う。
チェーン内の分散とチェーン間の分散を比較し、R_hat=1を目指す(1.1未満であれば良好でこれより大きいと収束していない可能性がある)また、事後分布の並列サンプリングを平均, 50%HPR, 95%HPRを出力する。
mc_errorはサンプリングによってもたらされた誤差で、サンプルが本当は互いに独立ではないことが考慮された値である。これはブロックnのそれぞれの平均xについての標準偏差で、各ブロックはチェインの一部になっている。
この誤差は結果に望む精度を下回っている必要がある。サンプリングは確率的で各試行ごとに異なる値となるが、別の試行と似た値になっているはずである。似ていないのであれば、サンプリング不足である。

$$\texttt{mc\_error}= \frac{σ(x)}{\sqrt{n}}$$

print(az.summary(chain_m))
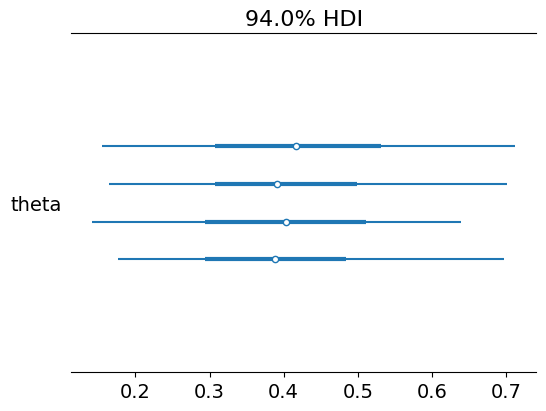
az.plot_forest(chain_m, var_names="theta")

output

        mean     sd  hdi_3%  hdi_97%  mcse_mean  mcse_sd  ess_bulk  ess_tail  \
theta  0.406  0.146   0.129     0.67      0.005    0.004     867.0    1057.0   

       r_hat  
theta    1.0  

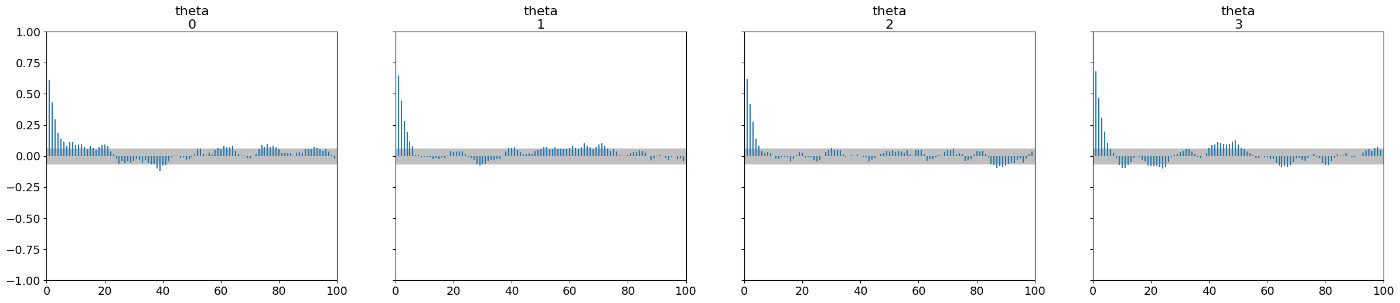
自己相関: 理想的なサンプリングでは自己相関(ある点の数値は別の点と依存していること)がない。メトロポリスヘイスティングなどの手法ではパラメータが他のパラメータと相関している可能性があるため、これを調べる。
最初の方のサンプルでは自己相関が高く、徐々に小さくなっていくという特性があるため、精度を求めるとき、自己相関が無いようにサンプルを多く取らざるを得なくなる。

az.plot_autocorr(chain)

有効サイズ: 自己相関があるサンプルでは自己相関の無いサンプルと比べて少ない情報しか持っていない。自己相関がないサンプルと同じ情報を持つにはどれだけのサンプルサイズが必要になるかを調べる。両者はおなじになることが望まれる。
分散の平均値を求めるには有効サイズは100以上である。
分布の両端に依存するし信用区間などを求めるには1000~10000はいる。

効率的なサンプラーを使うか、もしくはメモリ節約のためチェーンを間引くことが対処策としてある。

# arviz.ess(data, *, var_names=None, method='bulk', relative=False, prob=None, dask_kwargs=None)
# Calculate estimate of the effective sample size (ess).

print(az.ess(chain_m))

# Data variables:
# theta 798.7
# このとき1000のサンプルに対して自己相関のせいで799個のサンプル分しか情報が無いことになっている。

3. 事後分布の要約

まず信用区間を見てみる。このとき2値変数などの予測ではどちらに行くかを予測しなければならないことがある。

実質同値域(region of partical equivalence; ROPE): 信用区間に対して、完全に重なっているなら仮説を受理、重なっていないなら仮説を棄却、一部だけ重複しているようなときはどちらとも言えない。

• 重複: コインは公正で、五分五分で裏表がでる
• 重複しない: コインは不正で、どちらかに偏っている
• 一部重複: どちらとも言えない

az.plot_posterior(chain, rope=[0.45, 0.55])

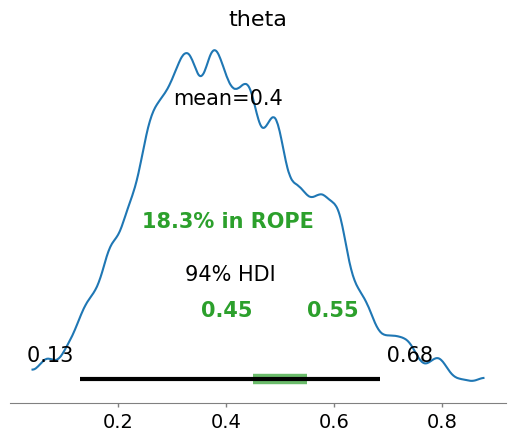
参照点を与えると、参照点より大きい場合の事後確率と小さい場合の事後確率も合わせて表示される。

az.plot_posterior(chain, ref_val=0.5)

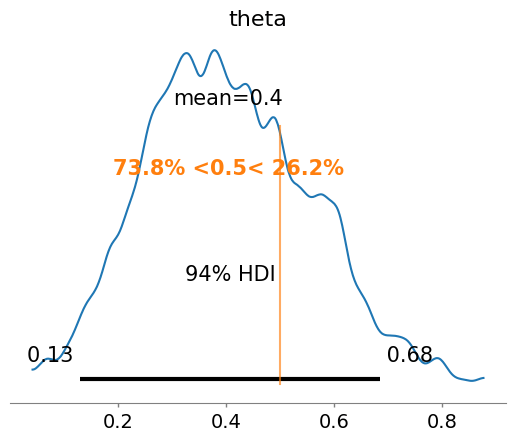
複数パラメータと階層モデル

次のライブラリを使用する。

import matplotlib.pyplot as plt
import numpy as np
from scipy import stats
import pandas as pd
import seaborn as sns

import pymc as pm
import arviz as az

迷惑パラメータ: ガウス分布などで平均が知りたい時、分散には興味はないが設定しなければならない。これはモデリング上必要だが関心がなくてもこれを推定しないといけない事になり、重荷である。

ベイズでは任意の未知パラメータを同じように扱い、不確実性をパラメータに吸収させることで大体うまくいくように推定される。

複数パラメータのベイズの定理は次の式で表され、パラメータは1次元の量であるとする。パラメータ$θ_2$が迷惑パラメータとすると、周辺化で以下のようにできる。
周辺化では$θ_2$に関する全ての値に対して事後分布を積分することとなるため、暗黙のうちに$θ_2$の不確実性を考慮していることになる。

$$p(θ_1,θ_2|y) ∝ p(y|θ_1,θ_2)p(θ_1,θ_2) \\ p(θ_1|y) = \int p(θ_1,θ_2|y) dθ_2$$

1. 正規化

ベータ分布と二項分布は取り扱いが楽で、また同様にガウス分布も数学的な扱いの良さがある。
ガウス分布は中心極限定理により十分なサンプルサイズのもとで多くの分布を近似できる。

ガウシアン推論

データがガウス分布に従う仮定でモデリングする。平均値と偏差を知らないため、この近似ガウス分布を用意する。

• $μ \sim \text{Uniform}(\text{low}, \text{high})$: 区間[low, high]に定義される一様分布
• $σ \sim \text{halfNormal}(σ_0)$: 正の定義域の正規分布
• $y \sim \text{Normal}(μ, σ)$

ここでlowやhighに事前知識をもたせて区間を狭めることで不確実性を減らすことができる。
$σ_0$は今回わからないので、とりあえず大きめに設定する。

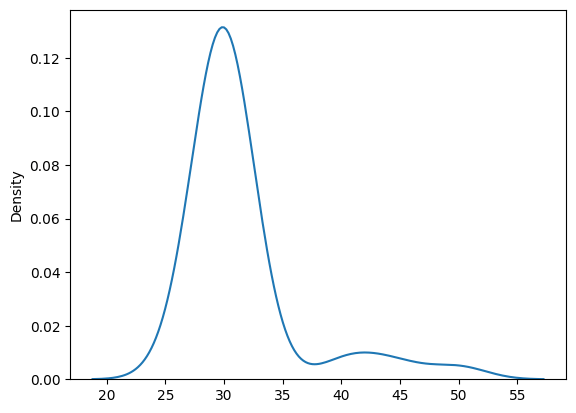
data = np.array([
    28, 32, 28, 29, 29, 30, 30, 28, 30, 30, 31, 29, 29, 31, 30, 30, 30, 32, 
    30, 30, 30, 29, 29, 30, 31, 31, 29, 31, 26, 32, 30, 30, 50, 40, 45, 42,
    ])
sns.kdeplot(data)

with pm.Model() as model_g:
    mu = pm.Uniform("mu", 0, 100)
    sigma = pm.HalfNormal("siguma", sigma=10)
    y = pm.Normal("y", mu=mu, sigma=sigma, observed=data)
    trace_g = pm.sample(1000)

chain_g = trace_g  # バーンインで最初のサンプルは削ると精度が良くなる trace_g[burnin:]
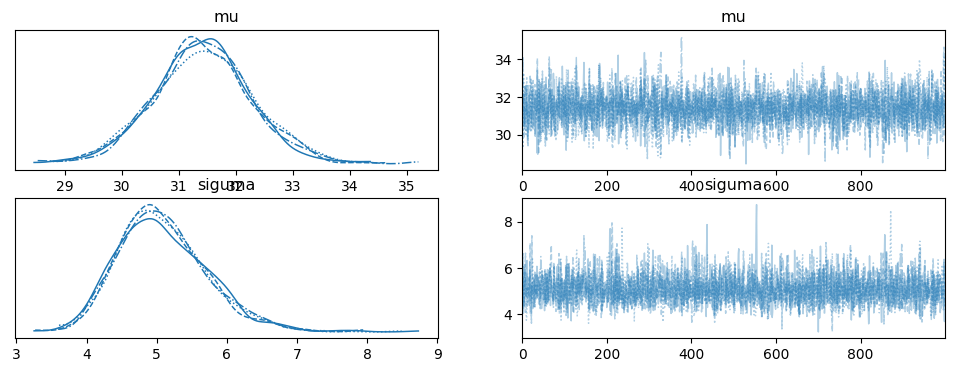
az.plot_trace(chain_g)
pm.summary(chain_g)

output

        mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
mu	31.416	0.867	29.867	33.146	0.014	0.010	3695.0	2562.0	1.0
siguma	5.086	0.630	4.004	6.273	0.012	0.008	2973.0	2556.0	1.0

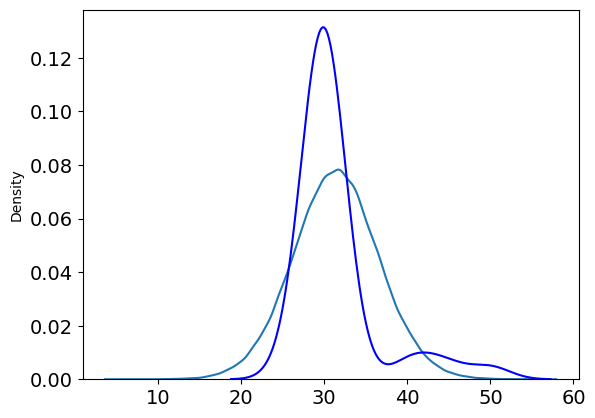
モデルの性能の確認のため、事後分布からサンプルして分布の形状を調べる。

y_pred = pm.sample_posterior_predictive(trace=chain_g, model=model_g)
# y_pred = y_pred["posterior_predictive"]["y"]  # arviz.InferenceData -> array[4, 1000, 36]

az.plot_dist(y_pred["posterior_predictive"]["y"])
sns.kdeplot(data, c="b")

az.plot_posterior(chain_g)

2. ロバスト推論

データの外れ値を減らすことよりもモデルの分布を使ってロバストに推論できる方が良い。
ベイジアンでは外れ値削除やヒューリスティックのその場しのぎの方法ではなく、異なる事前分布や尤度を直接的に仮定してモデリングでロバスト性を高める方法を好む。

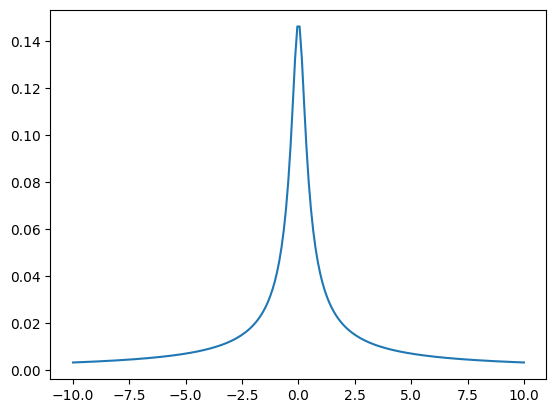
T分布: 平均とスケール(分散に似たもの)と自由度のパラメータを持つ。

• v = 1 で正規分布に等しくなる。vが大きいと裾野が大きくなり平均の周りに値が集中しなくなる
• v < 1 では平均が定義されず、サンプリングも収束しない
• v ≥ 2 では分散が定義されない。v→∞おいて自由度とスケールは等しくなる

x = np.linspace(-10,10,200)
x_pdf = stats.t(0.1).pdf(x)
plt.plot(x, x_pdf)
plt.show()
x_pdf = stats.t(1).pdf(x)

x_pdf = stats.t(100).pdf(x)
plt.plot(x, x_pdf)
plt.show()

T分布を用いてデータから事後分布を得る。

• $μ \sim \text{Uniform}(\text{low}, \text{high})$
• $σ \sim \text{HalfNormal}(σ_0)$
• $v \sim \text{Expnent}(λ)$: 指数分布
• $y \sim \text{Student}T(μ, σ, v)$

with pm.Model() as model_t:
    mu = pm.Uniform("mu", 28, 32)
    sigma = pm.HalfNormal("siguma", sigma=1)
    nu = pm.Exponential("nu", lam=1/30) 
    y = pm.StudentT("y", mu=mu, sigma=sigma, nu=nu, observed=data)

    trace_t = pm.sample(1000)

chain_t = trace_t
az.plot_trace(chain_t)

az.summary(chain_t)

output

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
mu	30.000	0.000	30.000	30.000	0.000	0.000	3693.0	2775.0	1.02
siguma	0.000	0.000	0.000	0.000	0.000	0.000	5.0	19.0	2.92
nu	0.111	0.017	0.087	0.132	0.008	0.006	4.0	12.0	3.42

az.plot_posterior(chain_t)

(何故かうまく行っていない... 要調整)

3. グループ間の比較

頻度論の仮説検定のシナリオでの定式化では、統計的有意性のみに囚われ、P値については誤った解釈が蔓延している。グループの比較に効果量を知ることで、現象の強さや大きさを数量的に推定する。

集団を以下に分けて、コントロールグループには何もしなかったり、偽物を与えたり、既存の効果を与える。

• 効果を受けるグループ(treatment group)
• 効果を受けないグループ(control group)

チップデータセットを用いて、今回はコントロールグループは無しで、トリートメントグループのみが存在する観察実験を行い、この概念を考えていく。

tips = sns.load_dataset("tips")
print(tips)

sns.violinplot(x="day", y="tip", data=tips)

output

     total_bill   tip     sex smoker   day    time  size
0         16.99  1.01  Female     No   Sun  Dinner     2
1         10.34  1.66    Male     No   Sun  Dinner     3
2         21.01  3.50    Male     No   Sun  Dinner     3
3         23.68  3.31    Male     No   Sun  Dinner     2
4         24.59  3.61  Female     No   Sun  Dinner     4
..          ...   ...     ...    ...   ...     ...   ...
239       29.03  5.92    Male     No   Sat  Dinner     3
240       27.18  2.00  Female    Yes   Sat  Dinner     2
241       22.67  2.00    Male    Yes   Sat  Dinner     2
242       17.82  1.75    Male     No   Sat  Dinner     2
243       18.78  3.00  Female     No  Thur  Dinner     2
[244 rows x 7 columns]

処理を簡単にするため、tipの合計をyとして、カテゴリを表すダミー変数をidxとする
(つまり、曜日を1~4の変数で扱う)。
このとき、μとσが1次元ではなく4次元ベクトルになる。

data_chip = tips["tip"].values
idx = pd.Categorical(tips["day"]).codes

print(data_chip)
print(idx)

output

[ 1.01  1.66  3.5   3.31  3.61  4.71  2.    3.12  1.96  3.23  1.71  5.
  1.57  3.    3.02  3.92  1.67  3.71  3.5   3.35  4.08  2.75  2.23  7.58
...
  3.    1.5   1.44  3.09  2.2   3.48  1.92  3.    1.58  2.5   2.    3.
  2.72  2.88  2.    3.    3.39  1.47  3.    1.25  1.    1.17  4.67  5.92
  2.    2.    1.75  3.  ]
  
[3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 2 2 2 2 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
...
 3 3 3 3 3 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 1
 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 0]

with pm.Model() as model_cg:
    mean = pm.Normal("mean", mu=0, sigma=10, shape=len(set(idx))) 
    sigma = pm.HalfNormal("sigma", sigma=10, shape=len(set(idx)))
    y = pm.Normal("y", mu=mean[idx], sigma=sigma[idx], observed=data_chip)
    
    trace_cg = pm.sample(2000)

chain_cg = trace_cg
az.plot_trace(chain_cg)

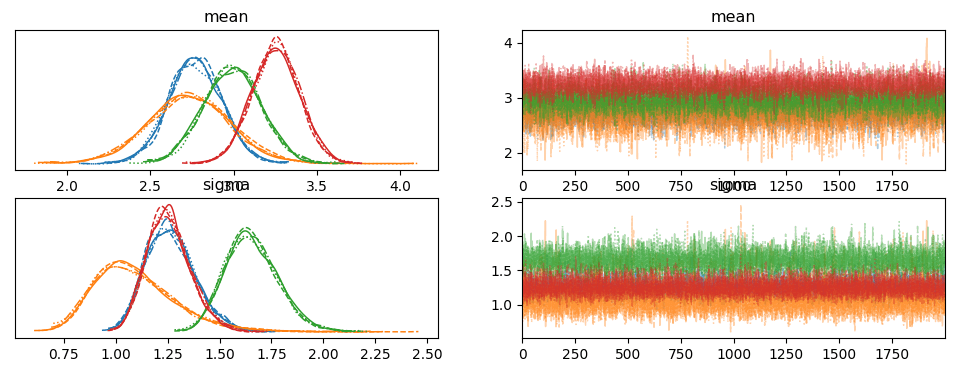
az.summary(chain_cg)

output

mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
mean[0]	2.771	0.161	2.465	3.072	0.002	0.001	10755.0	6563.0	1.0
mean[1]	2.734	0.255	2.257	3.217	0.003	0.002	7372.0	4835.0	1.0
mean[2]	2.993	0.173	2.662	3.309	0.002	0.001	8799.0	6059.0	1.0
mean[3]	3.252	0.143	2.989	3.524	0.001	0.001	9559.0	5238.0	1.0
sigma[0]	1.265	0.118	1.056	1.492	0.001	0.001	8867.0	6270.0	1.0
sigma[1]	1.096	0.203	0.752	1.470	0.002	0.002	8479.0	5327.0	1.0
sigma[2]	1.654	0.127	1.430	1.899	0.001	0.001	9244.0	6390.0	1.0
sigma[3]	1.256	0.104	1.063	1.453	0.001	0.001	9457.0	5990.0	1.0

y_pred = pm.sample_posterior_predictive(trace=chain_cg, model=model_cg)
az.plot_ppc(y_pred)
y_pred = y_pred["posterior_predictive"]["y"]  # arviz.InferenceData -> xarray.Dataset -> array[4, 2000, 244]

i = 0  # 曜日
data_chip_i = data_chip[idx == i]  # 曜日のダミー変数がiのものを選択
sns.kdeplot(data_chip_i, c="b")

y_pred_i = np.mean(y_pred[i], axis=1)
sns.kdeplot(y_pred_i, c="r")

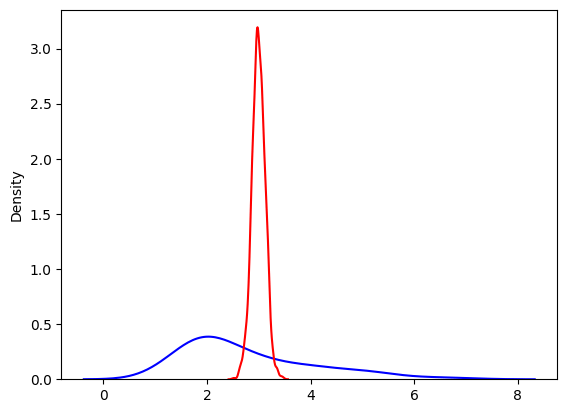
HPD参照値重複基準: 95%HPD(信用区間)が参照値を含んでいるかどうかを判断する。含んでいるなら差は無いと判断できる。

今回のデータでは95%HPDが参照値0を含んでいないのは木曜と日曜のチップ額のみで、他の曜日の組み合わせには差はないと言っていい。

コーエンのd: 2つのグループの平均値の差を両グループの分散の平均値で割ったもの。また、これはZスコア(標準化された値)として効果量を表す値に解釈できる。

$$d = \frac{μ_1 - μ_2}{\sqrt{\frac{σ_1^2 - σ_2^2}{2}}}$$

グループ比較では分散をもちいて各グループの変動(variability)を考慮する。例えば、

• あるグループの他のグループへのx単位の変化は個々のデータ点のちょうどx単位の変更によって説明できる(?)
• 言い換えると、x単位の半分が0に変更され、それ以外の半分は2x単位の変更によって説明される(?)
• コーエンのd = 0.1は各グループの標準偏差の差が0.1だったことを示す

優越率(probability of superiority; ps): コーエンのdに関連して効果量を表す指標で、あるグループか抽出したデータの値がほかグループのそれより大きい確率を表す。累積ガウス分布上のコーエンのd/√2がその確率である。

$$\text{ps} = Φ(\frac{d}{\sqrt{2}})$$

例えば優越率0.8であれば、他のグループのデータの値より大きい確率は80%であり、つまりそのグループは他のグループと比べて大きめである。

chain_cg_post = chain_cg["posterior"]
dist = stats.norm()

print(chain_cg_post["mean"].shape)  # chain_cg_post (4, 2000, 4) -> mean_diff (4, 4)

i = 1  # 比較グループi
j = 2  # 比較グループj
mean_diff = chain_cg_post["mean"][:,i] - chain_cg_post["mean"][:,j]
d_cohen = np.mean(mean_diff / np.sqrt((chain_cg_post["sigma"][:,i]**2 + chain_cg_post["sigma"][:,j]**2) / 2 ))
ps = dist.cdf(d_cohen / (2**0.5))  # 優越率

print("d_cohen: ", float(d_cohen))
print("ps: ", ps)

az.plot_posterior(chain_cg_post, ref_val=0, figsize=None)  
# 本来は、mean_diffのμ(i)-μ(j)の3!=6個のグラフで
# 0付近で標準化された分布が出てきて
# ref_val=0を含んでいるかどうかがプロットされてほしい...

output

(4, 2000, 4)
d_cohen:  -0.01754306974469938
ps:  0.49505131831051935

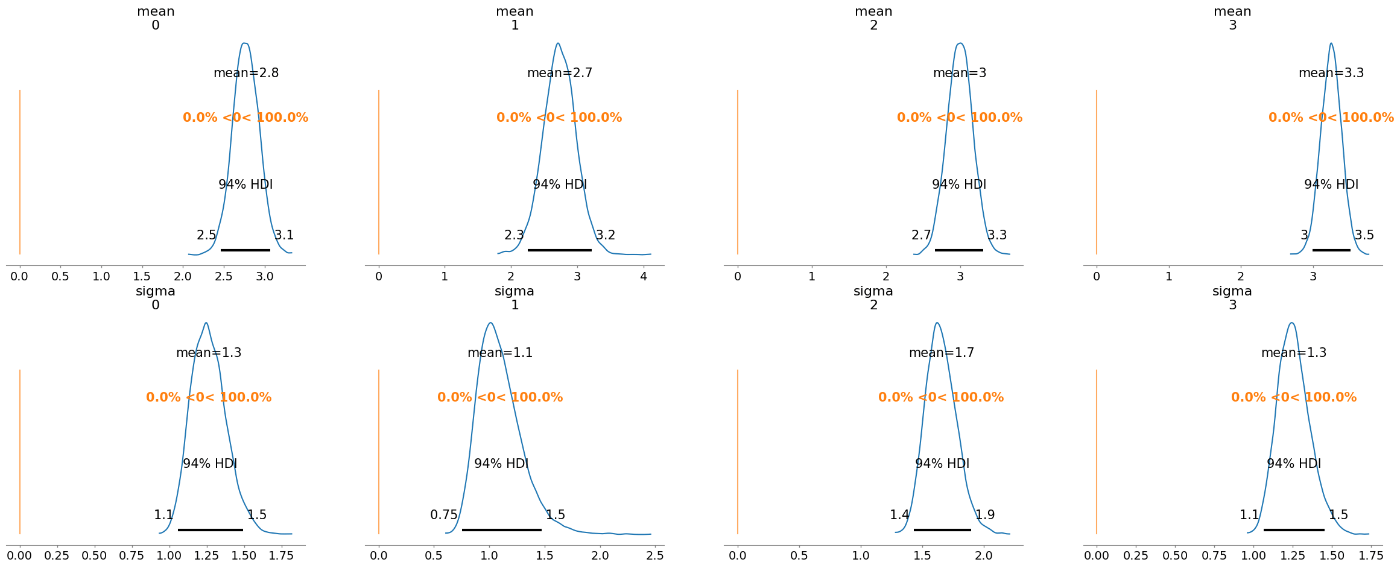
4. 階層モデル

大規模なデータをいろいろな場所でサンプルしたとき、別々のところからサンプルしたデータを分析することになり、各サンプルについて別々に変数推定する方法とデータ全体をプーリング(同じ特徴カテゴリに属するものを結合して1つのデータセットにまとめる)することが考えられる。
各個の分析では詳細な視点の分析ができるが、プーリングしたほうがサンプルサイズが大きいため正確な推定ができそうである。

このとき、ベイジアンでは階層モデル(hierarchical model) をモデリングすることで解決する。事前分布への事前分布(ハイパー事前分布)を仮定する方法である。あんまり複雑にすると解釈できなくなるので、程々にすること。

同じ都市の3つの水域から水をサンプルして鉛の濃度を調べる実験を考える。
ある基準を下回るサンプルには1、超えるサンプルには0が割り当てられる。

• $α \sim \text{HalfCauchy}(β_1)$: 半コーシー分布
• $β \sim \text{HalfCauchy}(β_2)$: 半コーシー分布
• $θ \sim \text{Beta(α,β)}$
• $y \sim \text{Bern(θ)}$: ベルヌーイ分布

sample_n = [30, 30, 30]  # サンプルの総数
sample_g = [18, 9, 3]  # 良好な水質のサンプル数

group_idx = np.repeat(np.arange(len(sample_n)), sample_n)
data = []
for i in range(0, len(sample_n)):
    data.extend( np.repeat([0,1], [sample_g[i], sample_n[i] - sample_g[i]]) )

print(data)

with pm.Model() as model_h:
    alpha = pm.HalfCauchy("alpha", beta=10)
    beta = pm.HalfCauchy("beta", beta=10)
    theta = pm.Beta("theta", alpha=alpha, beta=beta, shape=len(sample_n))
    y = pm.Bernoulli("y", p=theta[group_idx], observed=data)
    
    trace_h = pm.sample(2000)

chain_h = trace_h
az.plot_trace(chain_h)

az.summary(chain_h)

output

	mean	sd	hdi_3%	hdi_97%	mcse_mean	mcse_sd	ess_bulk	ess_tail	r_hat
alpha	8.754	6.760	0.579	20.336	0.230	0.201	1622.0	936.0	1.0
beta	4.319	3.255	0.237	10.157	0.109	0.095	1518.0	918.0	1.0
theta[0]	0.474	0.088	0.307	0.637	0.002	0.001	3265.0	1480.0	1.0
theta[1]	0.690	0.077	0.545	0.828	0.001	0.001	4776.0	4546.0	1.0
theta[2]	0.837	0.067	0.715	0.956	0.001	0.001	3044.0	2286.0	1.0

収縮(shrinking): 推定時に各グループがハイパー事前分布を通じて情報を共有すること。

sample_g	theta
[3,3,3]	[0.1,0.1,0.1]
[18,18,18]	[0.6,0.6,0.6]
[18,3,3]	[0.53,0.14,0.14]

表を見ると、上2行から、水質3ならθ=0.1・水質18ならθ=0.6であると推測されるが、サンプル場所で差がある3行目[18,3,3]を見ると、[0.6,0.1,0.1]ではなく[0.53,0.14,0.14]という値になっている。

これはトレースの収束やバグの問題ではなく、推定値が他の平均値に向かって収縮した結果である。ハイパラメータを組み込んだことにより、各グループが情報を共有し合い、データそれ自体からベータ分布の事前分布を推定している。

収縮の規模はデータに依存する。似ているグループ同士が互いの情報を共有することでロバスト性が高まるが、逆に似ていないグループの影響を弱めてしまう。
ハイパー事前分布の適切な設計でロバスト性を保持しながら似ていないグループの情報を削らないようにできる。

# θの事前分布を出力する
x = np.linspace(0, 1, 100)
print(chain_h["posterior"]["alpha"])
print(chain_h["posterior"]["beta"])

dist = stats.beta(chain_h["posterior"]["alpha"].mean(), chain_h["posterior"]["beta"].mean())
pdf = dist.pdf(x)
mode = x[np.argmax(pdf)]
mean = dist.moment(1)
plt.plot(x, pdf)

output

<xarray.DataArray 'alpha' (chain: 4, draw: 2000)>
array([[ 7.07003134,  3.4044857 ,  8.59753826, ..., 11.07907814,
         5.1979189 ,  2.32526128],
       [12.05710287,  3.54589777,  3.57359557, ...,  6.50788697,
        10.83117373,  2.55438068],
       [ 2.63961709,  4.96283771,  2.51359427, ..., 12.2457673 ,
         4.90402543,  6.69161446],
       [ 4.48777316, 23.31995032, 23.31995032, ...,  6.51108244,
         5.36163564,  2.17656506]])
Coordinates:
  * chain    (chain) int64 0 1 2 3
  * draw     (draw) int64 0 1 2 3 4 5 6 7 ... 1993 1994 1995 1996 1997 1998 1999
<xarray.DataArray 'beta' (chain: 4, draw: 2000)>
array([[ 1.5165571 ,  1.94188159,  3.81993281, ...,  7.82051895,
         1.53765102,  1.01935233],
       [ 5.29036964,  3.31200271,  2.70365444, ...,  2.69578389,
         3.12212964,  1.59569555],
       [ 2.0531695 ,  3.27275273,  1.59044473, ...,  4.29826333,
         2.90359889,  5.52856328],
       [ 2.94143141, 10.30896097, 10.30896097, ...,  2.31345553,
         2.31234663,  0.95148677]])
Coordinates:
  * chain    (chain) int64 0 1 2 3
  * draw     (draw) int64 0 1 2 3 4 5 6 7 ... 1993 1994 1995 1996 1997 1998 1999

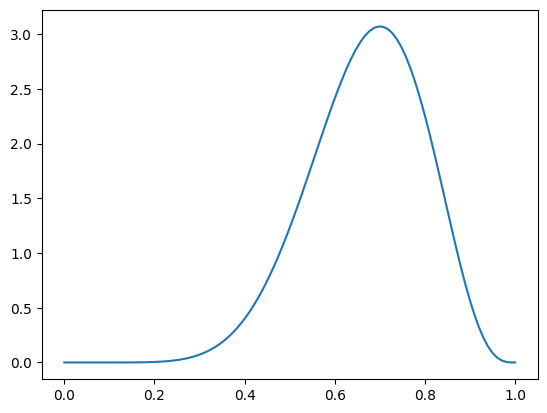
感想

• PyMCを使えば複数パラメータのモデル構築も簡単
• 事後分布から周辺分布を得るにはトレースを指標化すればいい
• ロバスト性には正規分布よりT分布を使うと良い
• グループ間の比較にはどれほどの違いがあるかを示す効果量を使う
• 階層モデルを使えばグループから情報をプールして、良い推論と収縮した推測値を得られる