🏐
Sparse Estimation with Python 勉強ノート 2.2 Lasso回帰の実装

2025/02/19に公開
鈴木讓 著

スパース推定100問 with Python

2021-01-29

https://www.kyoritsu-pub.co.jp/book/b10003298.html
Christopher M. Bishop 著, 元田浩 栗田多喜夫 樋口知之 松本裕治 村田昇 監訳

パターン認識と機械学習 ベイズ理論による統計的予測 (Pattern Recognition and Machine Learning)

2012-01-20

https://www.maruzen-publishing.co.jp/item/?book_no=294524
以前の記事をまとめて、Lasso回帰とLasso-Logistic回帰を実装します。

PRMLを読みながらスパース推定100問の行間を補完し、プログラムの見通しを良くしたいです。
以下はこの記事で使うパッケージ
import numpy as np
import polars as pl
from matplotlib import pyplot as plt

 1. Lasso回帰
 Lasso回帰の一般化表現の導出入力データ X∈RN×D\bm{X} \in \mathbb{R}^{N × D}X∈RN×D , y∈RN\bm{y} \in \mathbb{R}^{N}y∈RN とする。

データが平均 f(x,w)=∑d=1Dxdwdf(\bm{x},\bm{w}) = \sum_{d=1}^D x_d w_df(x,w)=∑d=1D​xd​wd​ 分散 βββ の正規分布に従い、またパラメータ w\bm{w}w は平均 000 分散 ααα のラプラス分布に従うモデルを考える。この w\bm{w}w に関する事前分布は、 www の多くは0であることを条件づけている。

この時、MAP推定により次の損失関数が導かれる。
p(w∣X,y,β)∝p(y∣X,w,β)p(w∣α)=∏n=1NN(yn∣f(xn,w),β−1)∏d=1DLaplace(wd∣0,α−1)=∏n=1Nβ2πe−β2(yn−f(xn,w))2∏d=1Dα2e−α∣wd∣∂∂wln⁡p(w∣X,y,β)=−∂∂w(β2∑n=1N(yn−f(xn,w))2+α∑d=1D∣wd∣⏟:=βE(w))=0↓λ:=α/βE(w)=12∣∣y−Xw⏟f(X,w)∣∣2+λ∣∣w∣∣L1
\begin{align*}
p(\bm{w}|\bm{X},\bm{y},β) & ∝ p(\bm{y}|\bm{X},\bm{w},β) p(\bm{w}|α)  \\
& = \prod_{n=1}^N \mathcal{N}(\bm{y}_n|f(\bm{x}_n,\bm{w}), β^{-1}) \prod_{d=1}^D \text{Laplace}(\bm{w}_d|0, α^{-1})  \\
& = \prod_{n=1}^N \sqrt{\frac{β}{2π}} e^{-\frac{β}{2}(y_n - f(\bm{x}_n,\bm{w}))^2} \prod_{d=1}^D \frac{α}{2} e^{-α|w_d|}  \\
\frac{∂}{∂\bm{w}} \ln p(\bm{w}|\bm{X},\bm{y},β) & = - \frac{∂}{∂\bm{w}}(\underbrace{\frac{β}{2}\sum_{n=1}^N(y_n - f(\bm{x}_n,\bm{w}))^2 + α \sum_{d=1}^D|w_d|}_{:=βE(\bm{w})}) = 0  \\
& ↓ \quad λ := α/β  \\
E(\bm{w}) & = \frac{1}{2}||\bm{y} - \underbrace{\bm{X} \bm{w}}_{f(\bm{X},\bm{w})}||^2 + λ ||\bm{w}||_{\text{L1}}
\end{align*}
p(w∣X,y,β)∂w∂​lnp(w∣X,y,β)E(w)​∝p(y∣X,w,β)p(w∣α)=n=1∏N​N(yn​∣f(xn​,w),β−1)d=1∏D​Laplace(wd​∣0,α−1)=n=1∏N​2πβ​​e−2β​(yn​−f(xn​,w))2d=1∏D​2α​e−α∣wd​∣=−∂w∂​(:=βE(w)2β​n=1∑N​(yn​−f(xn​,w))2+αd=1∑D​∣wd​∣​​)=0↓λ:=α/β=21​∣∣y−f(X,w)Xw​​∣∣2+λ∣∣w∣∣L1​​中心化により w0w_0w0​ を消去し、Lassoの誤差関数 E(w)E(\bm{w})E(w) を、コレスキー分解を用いる表現で書き直すと以下のようになる。コレスキー分解において、 R∈RN×N\bm{R} \in \mathbb{R}^{N×N}R∈RN×N は各サンプルの重み付けと解釈することができる。
E(w)=12(y−Xw)⊤R(y−Xw)+λ∣∣w∣∣L1↑R=RCh⊤RCh,X′=RChX,y′=RChy=12∣∣y′−X′w∣∣2+λ∣∣w∣∣L1
\begin{align*}
E(\bm{w}) & = \frac{1}{2} (\bm{y}-\bm{X}\bm{w})^\top \bm{R} (\bm{y}-\bm{X}\bm{w}) + λ ||\bm{w}||_{\text{L1}}  \\
& ↑ \quad \bm{R} = \bm{R}_{\text{Ch}}^\top\bm{R}_{\text{Ch}}, \quad \bm{X}' = \bm{R}_{\text{Ch}}\bm{X}, \quad \bm{y}' = \bm{R}_{\text{Ch}}\bm{y}  \\
& = \frac{1}{2} || \bm{y}' - \bm{X}'\bm{w} ||^2 + λ ||\bm{w}||_{\text{L1}}
\end{align*}
E(w)​=21​(y−Xw)⊤R(y−Xw)+λ∣∣w∣∣L1​↑R=RCh⊤​RCh​,X′=RCh​X,y′=RCh​y=21​∣∣y′−X′w∣∣2+λ∣∣w∣∣L1​​また、MAP推定に戻ると、事後分布を最大化する w\bm{w}w を求めるため、L1ノルムの劣微分を含む条件式を求めると以下のようになる。
0=∂∂wE(w)=−∑n=1Nxnd(yn−∑d′≠dNxnd′wd′−xndwd)+λ{1wd>0[−1,1]wd=0−1wd<0⇔wd=∑n=1Nxnd(yn−∑d′≠dNxnd′wd′)−λ{1wd>0[−1,1]wd=0−1wd<0
\begin{align*}
0 & = \frac{∂}{∂ \bm{w}} E(\bm{w})  \\
& = -\sum_{n=1}^N x_{nd} (y_{n} - \sum_{d' \neq d}^N x_{nd'} w_{d'} - x_{nd} w_{d}) + λ \left\lbrace \begin{matrix} 1 & w_d > 0 \\ [-1, 1] & w_d = 0 \\ -1 & w_d < 0 \end{matrix} \right.  \\
\Leftrightarrow w_d & = \sum_{n=1}^N x_{nd} (y_{n} - \sum_{d' \neq d}^N x_{nd'} w_{d'}) - λ \left\lbrace \begin{matrix} 1 & w_d > 0 \\ [-1, 1] & w_d = 0 \\ -1 & w_d < 0 \end{matrix} \right.
\end{align*}
0⇔wd​​=∂w∂​E(w)=−n=1∑N​xnd​(yn​−d′=d∑N​xnd′​wd′​−xnd​wd​)+λ⎩⎨⎧​1[−1,1]−1​wd​>0wd​=0wd​<0​=n=1∑N​xnd​(yn​−d′=d∑N​xnd′​wd′​)−λ⎩⎨⎧​1[−1,1]−1​wd​>0wd​=0wd​<0​​より簡潔に軟閾値作用素(Soft Thresholding Operator) Sλ(x)=sign(x)max⁡(∣x∣,λ)\mathcal{S}_λ(x) = \text{sign}(x) \max(|x|, λ)Sλ​(x)=sign(x)max(∣x∣,λ) を用いれば、 wdw_dwd​ は wdxndw_d x_{nd}wd​xnd​ 項を除く残差と xndx_{nd}xnd​ との内積を Sλ\mathcal{S}_λSλ​ で変換したものとして表せる。
この wdw_dwd​ について数値的に解くには、 wd′w_{d'}wd′​ を固定して wdw_dwd​ を更新し、 wdw_dwd​ が収束するまで繰り返す 座標降下法 を行う。

 Lasso回帰の実装def linear_lasso(x_feat, y_target, lambda_=1.0):
    N, D = x_feat.shape
    w = np.zeros(D)

    # 特徴を標準化
    x_feat_mean = x_feat.mean(axis=0, keepdims=True)
    x_feat_std = x_feat.std(axis=0, keepdims=True)
    x_feat = (x_feat - x_feat_mean) / x_feat_std

    # 座標降下法
    eps = 0.000001  # 収束判定条件
    w_old = np.ones_like(w)
    while np.linalg.norm(w - w_old) > eps:
        for d1 in range(D):
            y_d1 = y_target
            for d2 in range(D):
                y_d1 = (y_d1 - x_feat[:, d2] * w[d2]) if d1 != d2 else y_d1
            z = ((y_d1.T @ x_feat[:, d1:d1+1]) / N) / ((x_feat[:, d1:d1+1].T @ x_feat[:, d1:d1+1]) / N)
            w[d1] = np.sign(z[0,0]) * np.maximum(np.abs(z[0,0]) - lambda_, 0)  # L1 Norm部分の劣微分区間 [-λ, λ] → 0
            # ↑ maximum(a, b) == where(a > b, a, b)
        w_old = w
    
    # スケールを戻す
    w = w / x_feat_std
    w_0 = y_target.mean() - (x_feat_mean.T @ w)
    return w_0, w


def general_linear_lasso(x_feat, y_target, R=np.zeros(1), lambda_=1.0):
    N, D = x_feat.shape
    R = np.identity(N) if np.sum(R) == 0 else R
    is_diagonal = lambda matrix: np.all(matrix == np.diag(np.diagonal(matrix)))

    x_feat_mean = np.zeros((1, D))
    for d in range(D):
        x_feat_mean[:, d] = np.sum(R @ x_feat[:, d]) / np.sum(R)
        x_feat[:, d] = x_feat[:, d] - x_feat_mean[:, d]
    y_target_mean = np.sum(R @ y_target) / np.sum(R)
    y_target = y_target - y_target_mean

    R_ch = np.sqrt(R) if is_diagonal(R) else np.linalg.cholesky(R) # R が対角行列である場合 cholesky(R) は np.sqrt(R) と等価

    _, w = linear_lasso(R_ch @ x_feat, R_ch @ y_target, lambda_=lambda_)
    w_0 = y_target_mean - (x_feat_mean.T @ w)
    return w_0, w
以下ではBOSTON Datasetによる住宅価格の予測問題を2つの実装で解いている。

R=I\bold{R} = \bold{I}R=I である時2つの結果は同じになる。
# BOSTON Datasetをロード
data = pl.read_csv("boston.csv")
feat_name = ["crim", "zn", "indus", "chas", "rm", "age", "dis", "rad", "tax", "ptratio", "lstat"]
x_feat = data.select(feat_name).to_numpy()
y_target = data.select(["medv"]).to_numpy()
N, D = x_feat.shape

# λを変えながら回帰係数を計算
w_list_1 = []
w_list_2 = []
for l in range(10):
    _, w = linear_lasso(x_feat, y_target, lambda_=l)
    w_list_1.append(w)
    _, w = general_linear_lasso(x_feat, y_target, lambda_=l)
    w_list_2.append(w)
w_list_1 = np.concatenate(w_list_1)
w_list_2 = np.concatenate(w_list_2)

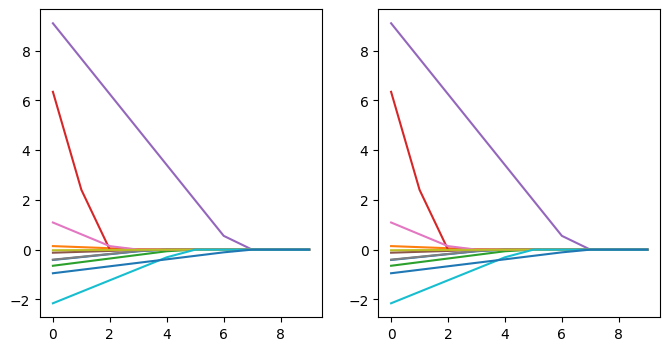
# グラフ描画
plt.figure(figsize=(8, 4))
plt.subplot(1, 2, 1)
for f in range(len(feat_name)):
    plt.plot(w_list_1[:, f])
plt.subplot(1, 2, 2)
for f in range(len(feat_name)):
    plt.plot(w_list_2[:, f])

 2. Lassoロジスティック回帰
 ロジスティック回帰の導出入力変数 x\bm{x}x について、それがクラス Cc\mathcal{C}_cCc​ に属している確率を p(Cc∣x)p(\mathcal{C}_c|\bm{x})p(Cc​∣x) とする。クラス Cc\mathcal{C}_cCc​ の事前分布を p(Cc)p(\mathcal{C}_c)p(Cc​) 、クラス Cc\mathcal{C}_cCc​ が生成するデータ x\bm{x}x の分布であるクラス内分布(クラスの条件付き確率分布)を p(x∣Cc)p(\bm{x}|\mathcal{C}_c)p(x∣Cc​) とすれば、ベイズの定理でこれらの関係を表現できる。

展開で出てくる p(x)p(\bm{x})p(x) は、周辺尤度として p(x∣Cc)p(Cc)p(\bm{x}|\mathcal{C}_c)p(\mathcal{C}_c)p(x∣Cc​)p(Cc​) から Cc\mathcal{C}_cCc​ を周辺化して削除した形で表現できる。
p(C1∣x)=p(x∣C1)p(C1)p(x)=p(x∣C1)p(C1)p(x∣C1)p(C1)+p(x∣C2)p(C2)=11+e−a⏟:=σ(a)a=ln⁡p(x∣C1)p(C1)p(x∣C2)p(C2)
\begin{align*}
p(\mathcal{C}_1|\bm{x}) & = \frac{p(\bm{x}|\mathcal{C}_1)p(\mathcal{C}_1)}{p(\bm{x})}  \\
& = \frac{p(\bm{x}|\mathcal{C}_1)p(\mathcal{C}_1)}{p(\bm{x}|\mathcal{C}_1)p(\mathcal{C}_1)+p(\bm{x}|\mathcal{C}_2)p(\mathcal{C}_2)}  \\
& = \underbrace{\frac{1}{1 + e^{-a}}}_{:= σ(a)}  \\
a & = \ln \frac{p(\bm{x}|\mathcal{C}_1)p(\mathcal{C}_1)}{p(\bm{x}|\mathcal{C}_2)p(\mathcal{C}_2)}
\end{align*}
p(C1​∣x)a​=p(x)p(x∣C1​)p(C1​)​=p(x∣C1​)p(C1​)+p(x∣C2​)p(C2​)p(x∣C1​)p(C1​)​=:=σ(a)1+e−a1​​​=lnp(x∣C2​)p(C2​)p(x∣C1​)p(C1​)​​p(C1∣x)p(\mathcal{C}_1|\bm{x})p(C1​∣x) は「入力 x\bm{x}x が得られた場合に x∈C1\bm{x} \in \mathcal{C}_1x∈C1​ である確率を表していて、上の式は ロジスティックシグモイド関数 σ(x)σ(x)σ(x) がそれと等価であることを示している。
クラス内分布 p(x∣Cc)p(\bm{x}|\mathcal{C}_c)p(x∣Cc​) を、平均 μc\bm{μ}_cμc​ 共分散(全クラスで共通と仮定) Σ\bm{Σ}Σ という設定にして、事後確率である入力に対するクラス分類 p(Cc∣x)p(\mathcal{C}_c|\bm{x})p(Cc​∣x) を導く。
まず2クラスの場合、 p(Cc∣x)=σ(a)p(\mathcal{C}_c|\bm{x}) = σ(a)p(Cc​∣x)=σ(a) より次のように求まる。
p(x∣C1)=N(x∣μ1,Σ)=1(2π)D/21(∣Σ∣)1/2e−12(x−μ1)⊤Σ−1(x−μ1)p(C1∣x)=σ(ln⁡p(x∣C1)p(C1)p(x∣C2)p(C2))=σ(−12μ1⊤Σ−1μ1+μ2⊤Σ−1μ2+ln⁡p(C1)p(C2)⏟:=w0+(Σ−1(μ1−μ2)⏟:=w)⊤x)=σ(w0+w⊤x)
\begin{align*}
p(\bm{x}|\mathcal{C}_1) & = \mathcal{N}(\bm{x}|\bm{μ}_1,\bm{Σ})  \\
& = \frac{1}{(2π)^{D/2}} \frac{1}{(|\bm{Σ}|)^{1/2}} e^{-\frac{1}{2} (\bm{x} - \bm{μ}_1)^\top \bm{Σ}^{-1} (\bm{x} - \bm{μ}_1)}  \\
p(\mathcal{C}_1|\bm{x}) & = σ(\ln \frac{p(\bm{x}|\mathcal{C}_1)p(\mathcal{C}_1)}{p(\bm{x}|\mathcal{C}_2)p(\mathcal{C}_2)})  \\
& = σ(
    \underbrace{
        -\frac{1}{2} \bm{μ}_1^\top \bm{Σ}^{-1} \bm{μ}_1 + \bm{μ}_2^\top \bm{Σ}^{-1} \bm{μ}_2 + \ln \frac{p(\mathcal{C}_1)}{p(\mathcal{C}_2)}
    }_{:= w_0} + ( \underbrace{
        \bm{Σ}^{-1} (\bm{μ}_1 - \bm{μ}_2)
    }_{:= \bm{w}} )^\top \bm{x}
)  \\
& = σ( w_0 + \bm{w}^\top \bm{x} )
\end{align*}
p(x∣C1​)p(C1​∣x)​=N(x∣μ1​,Σ)=(2π)D/21​(∣Σ∣)1/21​e−21​(x−μ1​)⊤Σ−1(x−μ1​)=σ(lnp(x∣C2​)p(C2​)p(x∣C1​)p(C1​)​)=σ(:=w0​−21​μ1⊤​Σ−1μ1​+μ2⊤​Σ−1μ2​+lnp(C2​)p(C1​)​​​+(:=wΣ−1(μ1​−μ2​)​​)⊤x)=σ(w0​+w⊤x)​ロジスティック回帰にシグモイドが現れることが示された。

 ロジスティック回帰の最適化xn\bm{x}_nxn​ に対して yn∈{0,1}y_n \in \{0, 1\}yn​∈{0,1} で表されるクラス属性のラベルが与えられ、 それらをまとめて X,y\bm{X}, \bm{y}X,y とする。

パラメータ w\bm{w}w の最適化では，対数尤度 ln⁡p(X,y∣w)\ln p(\bm{X},\bm{y}∣\bm{w})lnp(X,y∣w) がクロスエントロピー損失として導かれることを用いて、勾配が次のように表せる。
p(X,y∣w)=∏n=1Nσ(w⊤xn)yn(1−σ(w⊤xn))1−yn−ln⁡p(X,y∣w)=−∑n=1N(ynln⁡σ(w⊤xn)+(1−yn)ln⁡(1−σ(w⊤xn)))⏟:=E(w)←BinaryCrossEntropy(σ(w⊤xn),yn)∂E(w)∂w=−∑n=1N(yn−σ(w⊤xn⏟≡f(xn,w)))xn
\begin{align*}
p(\bm{X},\bm{y}|\bm{w}) & = \prod_{n=1}^N σ(\bm{w}^\top\bm{x}_n)^{y_n} (1-σ(\bm{w}^\top\bm{x}_n))^{1-y_n}  \\
- \ln p(\bm{X},\bm{y}|\bm{w}) & = \underbrace{- \sum_{n=1}^N (y_n \ln σ(\bm{w}^\top \bm{x}_n) + (1-y_n)\ln(1-σ(\bm{w}^\top \bm{x}_n))) }_{:= E(\bm{w}) ← \text{BinaryCrossEntropy}(σ(\bm{w}^\top\bm{x}_n), y_n)}  \\
\frac{∂E(\bm{w})}{∂\bm{w}} & = -\sum_{n=1}^N (y_n - σ( \underbrace{\bm{w}^\top \bm{x}_n}_{\equiv f(\bm{x}_n, \bm{w})} )) \bm{x}_n
\end{align*}
p(X,y∣w)−lnp(X,y∣w)∂w∂E(w)​​=n=1∏N​σ(w⊤xn​)yn​(1−σ(w⊤xn​))1−yn​=:=E(w)←BinaryCrossEntropy(σ(w⊤xn​),yn​)−n=1∑N​(yn​lnσ(w⊤xn​)+(1−yn​)ln(1−σ(w⊤xn​)))​​=−n=1∑N​(yn​−σ(≡f(xn​,w)w⊤xn​​​))xn​​シグモイドを含むBinaryCrossEntropyは w\bm{w}w に関する閉じた解を得られないため、IRLSを用いて反復的に最適化する。以下ではニュートンラフソン法の微分項を計算し、IRLSの正規方程式を得る。
E(w)=−∑n=1N(ynln⁡σ(w⊤xn)+(1−yn)ln⁡(1−σ(w⊤xn)))∂∂wE(w)=−∑n=1N(yn−σ(w⊤xn))xn=X⊤([σ(w⊤x1)⋮σ(w⊤xN)]⏟:=f−y)H=∂2∂w2E(w)=∑n=1Nσ(w⊤xn)(1−σ(w⊤xn))xnxn⊤=X⊤[σ(w⊤x1)(1−σ(w⊤x1))O⋱Oσ(w⊤xN)(1−σ(w⊤xN))]⏟:=RX
\begin{align*}
E(\bm{w}) & = - \sum_{n=1}^N (y_n \ln σ(\bm{w}^\top \bm{x}_n) + (1-y_n)\ln(1-σ(\bm{w}^\top \bm{x}_n)))  \\
\frac{∂}{∂\bm{w}} E(\bm{w}) & = - \sum_{n=1}^N (y_n - σ(\bm{w}^\top \bm{x}_n)) \bm{x}_n  \\
& = \bm{X}^\top ( \underbrace{ \begin{bmatrix}
σ(\bm{w}^\top \bm{x}_1)  \\
\vdots  \\
σ(\bm{w}^\top \bm{x}_N)  \\
\end{bmatrix} }_{:= \bm{f}} - \bm{y} )  \\
\bm{H} = \frac{∂^2}{∂\bm{w}^2} E(\bm{w}) & = \sum_{n=1}^N σ(\bm{w}^\top \bm{x}_n) (1 - σ(\bm{w}^\top \bm{x}_n)) \bm{x}_n \bm{x}_n^\top  \\
& = \bm{X}^\top \underbrace{ \begin{bmatrix}
σ(\bm{w}^\top \bm{x}_1) (1 - σ(\bm{w}^\top \bm{x}_1)) & & \bm{O}  \\
         & \ddots &           \\
\bm{O} &        & σ(\bm{w}^\top \bm{x}_N) (1 - σ(\bm{w}^\top \bm{x}_N))  \\
\end{bmatrix} }_{:= \bm{R}} \bm{X}
\end{align*}
E(w)∂w∂​E(w)H=∂w2∂2​E(w)​=−n=1∑N​(yn​lnσ(w⊤xn​)+(1−yn​)ln(1−σ(w⊤xn​)))=−n=1∑N​(yn​−σ(w⊤xn​))xn​=X⊤(:=f​σ(w⊤x1​)⋮σ(w⊤xN​)​​​​−y)=n=1∑N​σ(w⊤xn​)(1−σ(w⊤xn​))xn​xn⊤​=X⊤:=R​σ(w⊤x1​)(1−σ(w⊤x1​))O​⋱​Oσ(w⊤xN​)(1−σ(w⊤xN​))​​​​X​故に、IRLSの正規方程式は以下である。
wnew=wold−H−1∂∂wE(w)=wold−(X⊤RX)−1X⊤(f−y)=(X⊤RX)−1X⊤R(Xwold−R−1(f−y))⏟:=z
\begin{align*}
\bm{w}^{\text{new}} &= \bm{w}^{\text{old}} - \bm{H}^{-1} \frac{∂}{∂\bm{w}} E(\bm{w})  \\
& = \bm{w}^{\text{old}} - (\bm{X}^\top\bm{R}\bm{X})^{-1} \bm{X}^\top (\bm{f} - \bm{y})  \\
& = (\bm{X}^\top\bm{R}\bm{X})^{-1} \bm{X}^\top \bm{R} \underbrace{ (\bm{X}\bm{w}^{\text{old}} - \bm{R}^{-1}(\bm{f} - \bm{y})) }_{:= \bm{z}}
\end{align*}
wnew​=wold−H−1∂w∂​E(w)=wold−(X⊤RX)−1X⊤(f−y)=(X⊤RX)−1X⊤R:=z(Xwold−R−1(f−y))​​​以上により、 w\bm{w}w から R,z\bm{R}, \bm{z}R,z を求め、 R,z\bm{R}, \bm{z}R,z から w\bm{w}w を求めることを交互に繰り返すことで、ロジスティック回帰のパラメータが最適化される。

ここで求められる w^\hat{\bm{w}}w^ は 12(z−Xw)⊤R(z−Xw)\frac{1}{2} (\bm{z}-\bm{X}\bm{w})^\top \bm{R} (\bm{z}-\bm{X}\bm{w})21​(z−Xw)⊤R(z−Xw) を最小化する w\bm{w}w になっている。

 ロジスティック回帰の実装def vdiag(m: np.ndarray):
    return np.diag(m.squeeze())

def logistic_regression(x_feat, y_target):
    N, D = x_feat.shape
    x_feat_mean = x_feat.mean(axis=0, keepdims=True)
    x_feat_std = x_feat.std(axis=0, keepdims=True)
    x_feat = (x_feat - x_feat_mean) / x_feat_std

    w_old = np.zeros((D, 1))
    w_new = np.ones((D, 1))
    eps = 0.001
    while np.linalg.norm(w_old - w_new) > eps:
        w_old = w_new
        xw = x_feat @ w_old
        fy = 1 / (1 + np.exp(-xw)) - y_target
        R = vdiag((1 / (1 + np.exp(-xw))) * (1 - (1 / (1 + np.exp(-xw)))) + eps**4)
        z = xw - np.linalg.inv(R) @ fy
        w_new = np.linalg.inv(x_feat.T @ R @ x_feat) @ x_feat.T @ R @ z
    w = w_new

    print(w)
    pred = 1 / (1 + np.exp(-(x_feat @ w)))
    return pred


data = pl.read_csv("iris.csv")
x_feat = data[:100].select(["length0" ,"width0", "length1", "width1"]).to_numpy()
y_target = data[:100].select("variety").to_numpy()

pred = logistic_regression(x_feat, y_target)

print(np.where(pred > 0.5, 1, 0).reshape(-1))  # 予測ラベル
print(y_target.reshape(-1))  # クラスの正解ラベル
この結果
重み
[[-0.77190021]
 [-9.40190388]
 [20.14680524]
 [29.36256095]]

予測ラベル
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
正解ラベル
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]

 Lassoロジスティック回帰の導出ただし、 D>ND>ND>N となるシチュエーション(例えば遺伝子発現解析など)では尤度推定量 w^\hat{\bm{w}}w^ が際限なく大きくなるため、L1正則化を用いることで有効でない wdw_dwd​ が0になるようにしたい。

これは対数尤度(クロスエントロピー) E(w)E(\bm{w})E(w) へL1正則化項を加える。この導出はLasso回帰と同様に事前分布として w\bm{w}w へLapras分布を仮定することで簡単に導ける。
ここで、ロジスティック回帰の対数尤度を最小化する w^\hat{\bm{w}}w^ はIRLSにより求められ、これは同時に 12(z−Xw)⊤R(z−Xw)\frac{1}{2} (\bm{z}-\bm{X}\bm{w})^\top \bm{R} (\bm{z}-\bm{X}\bm{w})21​(z−Xw)⊤R(z−Xw) を最小化することが上でわかっているため、以下のように問題を書き換える事ができる。
ELasso(w)=−∑n=1N(ynln⁡σ(w⊤xn)+(1−yn)ln⁡(1−σ(w⊤xn)))+λ∣∣w∣∣L1≡12(z−Xw)⊤R(z−Xw)+λ∣∣w∣∣L1
\begin{align*}
E_{\text{Lasso}}(\bm{w}) & = - \sum_{n=1}^N (y_n \ln σ(\bm{w}^\top \bm{x}_n) + (1-y_n)\ln(1-σ(\bm{w}^\top \bm{x}_n))) + λ || \bm{w} ||_{\text{L1}}  \\
& \equiv \frac{1}{2} (\bm{z}-\bm{X}\bm{w})^\top \bm{R} (\bm{z}-\bm{X}\bm{w}) + λ || \bm{w} ||_{\text{L1}}
\end{align*}
ELasso​(w)​=−n=1∑N​(yn​lnσ(w⊤xn​)+(1−yn​)ln(1−σ(w⊤xn​)))+λ∣∣w∣∣L1​≡21​(z−Xw)⊤R(z−Xw)+λ∣∣w∣∣L1​​この最小化はロジスティック回帰と同様に、 w\bm{w}w から R,z\bm{R}, \bm{z}R,z を求め、その後 R,z\bm{R}, \bm{z}R,z から w\bm{w}w を最小化すれば良い。この時、問題を書き換えたことにより、w\bm{w}w の最小化については一般化されたLasso回帰と同じ計算により実現できるようになっている。

 Lassoロジスティック回帰の実装def lasso_logistic_regression(x_feat, y_target, lambda_=1.0):
    N, D = x_feat.shape
    x_feat_mean = x_feat.mean(axis=0, keepdims=True)
    x_feat_std = x_feat.std(axis=0, keepdims=True)
    x_feat = (x_feat - x_feat_mean) / x_feat_std

    w_old = np.zeros((D, 1))
    w_new = np.ones((D, 1))
    eps = 0.001
    while np.linalg.norm(w_old - w_new) > eps:
        w_old = w_new
        xw = x_feat @ w_old
        fy = 1 / (1 + np.exp(-xw)) - y_target
        R = vdiag((1 / (1 + np.exp(-xw))) * (1 - (1 / (1 + np.exp(-xw)))) + eps**4)
        z = xw - np.linalg.inv(R) @ fy
        _, w_new = general_linear_lasso(x_feat, z, R, lambda_=lambda_)
        w_new = w_new.reshape((D, 1))
    w = w_new

    print(w)
    pred = 1 / (1 + np.exp(-(x_feat @ w)))
    return pred


pred = lasso_logistic_regression(x_feat, y_target, lambda_=0.7)

print(np.where(pred > 0.5, 1, 0).reshape(-1))  # 予測ラベル
print(y_target.reshape(-1))  # クラスの正解ラベル
この結果
重み
[[ 0.        ]
 [-0.        ]
 [ 0.81276811]
 [ 0.79554075]]

予測ラベル
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
正解ラベル
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1]
以上のように、Lassoによる変数選択効果が働き、通常のロジスティック回帰の重み係数が小さい次元は無視され、重要な次元のみによる表現が行われる。

 感想この記事では以下2つの記事を俯瞰しながら、SEwPの行間をPRMLを読んで埋めてみた。
https://zenn.dev/inaturam/articles/34d7d3ce828e76
https://zenn.dev/inaturam/articles/02e22806c6d6bb
次は1章の残りのElasticNetによる回帰と、2章のポアソン回帰、生存時間解析などを書き下していきたい。

SEwPはトピックの提案が詳細で、1つのテーマから複数の話題を接種することができるのだが、数式の見通しの悪さが凶悪なため、他の書籍で理論を理解してから読まないとよくわからない感じになってしまう。PRMLの知識があれば第二章まではなんとかなりそうなのでもう少し読み進めてみるが、GroupLassoからはどうするか...
https://www.anarchive-beta.com/entry/2022/01/14/193000
この記事ではPRMLにおいてデータを基底関数 φφφ で飛ばした場合の決定境界の可視化がされている。

カーネルSVMなどでガウス関数などを φφφ に用いることで決定境界が曲面になることは感覚的にわかるが、これを各イテレーションでどのような形になるか可視化しているのはとてもわかりやすくて良かった。
Discussion

ログインするとコメントできます