鈴木讓 著
スパース推定100問 with Python
2021-01-29
https://www.kyoritsu-pub.co.jp/book/b10003298.html
Christopher M. Bishop 著, 元田浩 栗田多喜夫 樋口知之 松本裕治 村田昇 監訳
パターン認識と機械学習 ベイズ理論による統計的予測 (Pattern Recognition and Machine Learning)
2012-01-20
https://www.maruzen-publishing.co.jp/item/?book_no=294524
Lassoをロジスティック回帰に適用したものを勉強します。正直なところ難易度が高くて練習問題は全く解けていませんが、とりあえずどんな景色か見てみることを目標としています。
記法はPRML風にしますが、オリジナルな書き方も少しあります。
この記事でわかること
- 入力 \bold{x} を与えたとき、その入力が所属するクラスの確率 p(\mathcal{C}_1|\bold{x}) は、(クラス確率が正規分布でその共分散が各クラスで共通の場合)シグモイドを活性化関数とした一般化線形モデル σ(w_0 + \bold{w}^\top\bold{x}) として書ける。複数クラスの場合も同様に、softmaxを活性化関数とした一般化線形モデルとして書ける。
- 確率的生成モデルによる分類では、分布の各パラメータを個別に最尤推定することで、分布そのものをパラメトリックに復元し、データとクラスの分布を得ることができる。しかしパラメータ数はデータの次元に2乗オーダーで従うので、計算量は大きい。
- 確率的識別モデルによる分類は、特にロジスティック回帰が有名。一般化線形モデルとして設計したクラスの確率を使い、分布のパラメータではなくそれらを要約した線形モデルのパラメータ \bold{w} を最尤推定することで、入力の特徴次元の増加に対する計算量の増加が定数オーダーになる。
-
\bold{w} についての負の対数尤度 -\ln p(\bold{X},\bold{t}|\bold{w}) はクロスエントロピー誤差になり、その最大化のため勾配を計算すると、線形回帰の二乗和誤差の勾配 -\sum_{n=1}^N (t_n - \bold{w}^\top \bold{x}_n) と殆ど同じ形 -\sum_{n=1}^N (t_n - σ(\bold{w}^\top \bold{x}_n)) になる。
- クロスエントロピー誤差の最小化は閉じた形で得られないので、IRLSによって最適化する。IRLSでは2階微分の勾配を使ったヘッセ行列を用いて \bold{w} の更新式を計算する。それは \bold{w}^{\text{new}} = (\bold{X}^\top\bold{R}\bold{X})^{-1} \bold{X}^\top\bold{R} [\bold{X}\bold{w}^{\text{old}} - \bold{R}^{-1}(\bold{y} - \bold{t})] となり、対角行列 \bold{R} を分散として一般化した正規方程式として見ることができる。
- クロスエントロピー誤差にL1正則化を加えた誤差関数を最小化する場合、パラメータの更新は (\bold{z}-\bold{X}\bold{w}^{\text{old}})^\top \bold{R} (\bold{z}-\bold{X}\bold{w}^{\text{old}}) + λ ||\bold{w}^{\text{old}}||_{\text{L1}} の最小化を反復することに帰着し、これは \bold{R} と \bold{z} の計算により変数を置き換えた、単純な線形Lassoの誤差関数を解く計算になっている。
疎なロジスティック回帰
0. Lasso線形回帰の復習
まずデータとして入力変数 \bold{x}_n とそれに対応する目的変数 t_n を設定し、回帰関数 y(\bold{x},\bold{w}) を考える。
\begin{align*}
\bold{X} & = [ \bold{x}_n \in \mathbb{R}^{D} ] \in \mathbb{R}^{N×D} \\
& = \begin{bmatrix}
x_{1,1} & \dots & x_{N,1} \\
\vdots & \ddots & \vdots \\
x_{D,1} & \dots & x_{N,D} \\
\end{bmatrix} \\
\bold{t} & = [ t_n ] \in \mathbb{R}^{D} \\
y(\bold{x},\bold{w}) & = w_0 + \sum_{d=1}^D w_d x_d
\end{align*}
Lasso線形回帰は、線形回帰の尤度モデルに対し「パラメータ \bold{w} が0に偏って分布する」という信念を反映したラプラス分布を事前分布として、そのMAP推定に出てくるL1ノルム正則化項の劣微分が \bold{X} の特性により \bold{w} = 0 で閉区間を形成することから、パラメータをスパースにする。
まず、事後分布についての設定からL1正則化誤差関数 E を得る。
\begin{align*}
p(\bold{w}|\bold{X},\bold{t},β) & ∝ p(\bold{t}|\bold{X},\bold{w},β) p(\bold{w}|α) \\
& = \prod_{n=1}^N \mathcal{N}(\bold{t}_n|y(\bold{x}_n,\bold{w}), β^{-1}) \prod_{d=1}^D \text{Laplace}(\bold{w}_d|0, α^{-1}) \\
& = \prod_{n=1}^N \sqrt{\frac{β}{2π}} e^{-\frac{β}{2}(t_n - y(\bold{x}_n,\bold{w}))^2} \prod_{d=1}^D \frac{α}{2} e^{-α|w_d|} \\
\frac{∂}{∂\bold{w}} \ln p(\bold{w}|\bold{X},\bold{t},β) & = - \frac{∂}{∂\bold{w}}(\underbrace{\frac{β}{2}\sum_{n=1}^N(t_n - y(\bold{x}_n,\bold{w}))^2 + α \sum_{d=1}^D|w_d|}_{:=βE(\bold{w})}) = 0 \\
& ↓ \quad λ := α/β \\
E(\bold{w}) & = \frac{1}{2}||\bold{t} - y(\bold{X},\bold{w})||^2 + λ ||\bold{w}||_{\text{L1}}
\end{align*}
この誤差関数は、微分不可能な点を含む凸関数である絶対値を持っていて、通常の微分ではなく劣微分を使い劣勾配を求める。
劣微分(subderivative, subdifferential): 凸関数 f の劣微分 \frac{∂f(\bold{z})}{∂\bold{z}} とは、 f(z) - f(z_0) ≥ c (z-z_0) を満たすような c の集合であり、閉区間である。
c \in [\lim_{x\nearrow x_0} \frac{f(x) - f(x_0)}{x-x_0}, \lim_{x\searrow x_0} \frac{f(x) - f(x_0)}{x-x_0}]
直感的には、凸関数 f の微分不可能な点において、左側の勾配から右側の勾配に変化するまでにかかる傾きの変化と考えても良い。
https://qiita.com/wosugi/items/8d5a407a0a0434aaabeb
E の特徴次元 d の劣微分を用いることで、回帰パラメータ w_d の解を以下のように表せる。
\begin{align*}
0 & = \frac{∂}{∂w_d} E(w_d) \\
⇔ 0 & = \underbrace{\sum_{n=1}^N (t_n - \sum_{d'≠d}^D x_{n,d'}w_{d'}) x_{n,d}}_{:= φ} - w_d \sum_{n=1}^N x_{n,d}^2 + λ \begin{cases}
1 & w_d > 0 \\
[-1,1] & w_d = 0 \\
-1 & w_d < 0 \\
\end{cases} \\
⇔ w_d & = \begin{cases}
\frac{φ - λ}{\sum_{n=1}^N x_{n,d}^2} & λ < φ \\
0 & -λ ≤ φ ≤ λ \\
\frac{φ + λ}{\sum_{n=1}^N x_{n,d}^2} & φ < -λ \\
\end{cases}
\end{align*}
また、パラメータのバイアス項 w_0 は次のように計算できる。これは通常の線形回帰と同じ。
w_0 = \underbrace{\frac{1}{N} \sum_{n=1}^N t_n}_{:=\bar{t}} - \sum_{d=1}^D \underbrace{\frac{1}{N} \sum_{n=1}^N \bold{X}_{n,d}}_{:=\bar{x}_d} w_d
以上より、Lasso線形回帰の最適化においては、正則化パラメータとデータに依存する項の関係から λ < |φ| の区間で回帰パラメータが0に張り付くことがわかる。回帰関数への貢献度の小さい特徴次元のパラメータ w_d は0になり、それ以外のパラメータが誤差を最小化しようとする性質により、回帰モデルの最適化と同時に変数選択が行われるという結果を導いている。
Cholesky分解を使った形式
逆行列の数値計算を高速に行うためにはCholesky分解を使うことがある。
次の式は、コレスキー分解を考えたときのLassoの誤差関数の変形である。
\begin{align*}
E(\bold{w}) & = \frac{1}{2} (\bold{z}-\bold{X}\bold{w})^\top \bold{R} (\bold{z}-\bold{X}\bold{w}) + λ ||\bold{w}||_{\text{L1}} \\
& ↓ \quad \bold{R} = \bold{R}_{\text{Ch}}^\top\bold{R}_{\text{Ch}}, \quad \bold{X}' = \bold{R}_{\text{Ch}}\bold{X}, \quad \bold{t} = \bold{R}_{\text{Ch}}\bold{z} \\
& = \frac{1}{2} || \bold{t} - \bold{X}'\bold{w} ||^2 + λ ||\bold{w}||_{\text{L1}} \\
\end{align*}
1. 確率的生成モデルによる分類
分類のための手法としてロジスティックシグモイド関数と線形モデルを組み合わせる。
まず、簡単な確率的生成モデルの考え方からシグモイド関数と線形モデルの関係を導いて、その最尤推定によるパラメータ決定について考える。
モデルの設定
入力変数 \bold{x} について、それがクラス \mathcal{C}_c に属している確率を p(\mathcal{C}_c|\bold{x}) とする。クラス \mathcal{C}_c の事前分布を p(\mathcal{C}_c) 、クラス \mathcal{C}_c が生成するデータ \bold{x} の分布であるクラス内分布(クラスの条件付き確率分布)を p(\bold{x}|\mathcal{C}_c) とすれば、ベイズの定理でこれらの関係を表現できる。展開で出てくる p(\bold{x}) は、周辺尤度として分子 p(\bold{x}|\mathcal{C}_c)p(\mathcal{C}_c) から \mathcal{C}_c を周辺化して削除した形で使える。
まず、 C=2 の2値分類問題の場合は次のようになる。
\begin{align*}
p(\mathcal{C}_1|\bold{x}) & = \frac{p(\bold{x}|\mathcal{C}_1)p(\mathcal{C}_1)}{p(\bold{x})} \\
& = \frac{p(\bold{x}|\mathcal{C}_1)p(\mathcal{C}_1)}{p(\bold{x}|\mathcal{C}_1)p(\mathcal{C}_1)+p(\bold{x}|\mathcal{C}_2)p(\mathcal{C}_2)} \\
& = \underbrace{\frac{1}{1 + e^{-a}}}_{:= σ(a)} \\
a & = \ln \frac{p(\bold{x}|\mathcal{C}_1)p(\mathcal{C}_1)}{p(\bold{x}|\mathcal{C}_2)p(\mathcal{C}_2)}
\end{align*}
この事後分布の形はロジスティックシグモイド関数 σ(x)=\frac{1}{1+e^{-x}} として有名である。シグモイドは対称性を持ち、 σ(-x) = 1 - σ(x) が成立するので、2値分類においてよく現れる。
さらにクラス数を一般化して複数クラス分類について考えると、次のようになる。
\begin{align*}
p(\mathcal{C}_c|\bold{x}) & = \frac{p(\bold{x}|\mathcal{C}_c)p(\mathcal{C}_c)}{p(\bold{x})} \\
& = \frac{p(\bold{x}|\mathcal{C}_c)p(\mathcal{C}_c)}{\sum_{c'=1}^C p(\bold{x}|\mathcal{C}_{c'})p(\mathcal{C}_{c'})} \\
& = \underbrace{\frac{e^{a_{c}}}{\sum_{c'=1}^C e^{a_{c'}}}}_{:=\text{Softmax}_{c}(\bold{a})} \\
a_c & = \ln p(\bold{x}|\mathcal{C}_c)p(\mathcal{C}_c)
\end{align*}
これはソフトマックス関数 \text{Softmax}(\bold{x}) として有名である。
以上により、離散クラス分類を確率的に書き表すと、対数事後分布 p(\mathcal{C}_c|\bold{x}) にシグモイド・ソフトマックス系の関数形が現れることがわかった。
尤度の書き下し
クラス内分布 p(\bold{x}|\mathcal{C}_c) を、平均 \boldsymbol{μ}_c 共分散(全クラスで共通と仮定) \bold{Σ} という設定にして、事後確率である入力に対するクラス分類 p(\mathcal{C}_c|\bold{x}) を導く。
まず2クラスの場合、 p(\mathcal{C}_c|\bold{x}) = σ(a) より次のように求まる。
結果だけ言えば、共分散が全クラスで一致しているため \bold{x} の2次の項は消えてくれるのでシグモイドの中身が線形になり、決定境界が \bold{x} の線形モデルで与えられる平面になる。(逆に言うと、分散が共有でない場合は2次の項が残ることで決定境界が2次曲線になる)
\begin{align*}
p(\bold{x}|\mathcal{C}_c) & = \mathcal{N}(\bold{x}|\boldsymbol{μ}_c,\bold{Σ}) \\
& = \frac{1}{(2π)^{D/2}} \frac{1}{(|\bold{Σ}|)^{1/2}} e^{-\frac{1}{2} (\bold{x} - \boldsymbol{μ}_c)^\top \bold{Σ}^{-1} (\bold{x} - \boldsymbol{μ}_c)} \\
p(\mathcal{C}_1|\bold{x}) & = σ(\ln \frac{p(\bold{x}|\mathcal{C}_1)p(\mathcal{C}_1)}{p(\bold{x}|\mathcal{C}_2)p(\mathcal{C}_2)}) \\
& = σ(
\underbrace{
-\frac{1}{2} \boldsymbol{μ}_1^\top \bold{Σ}^{-1} \boldsymbol{μ}_1 + \boldsymbol{μ}_2^\top \bold{Σ}^{-1} \boldsymbol{μ}_2 + \ln \frac{p(\mathcal{C}_1)}{p(\mathcal{C}_2)}
}_{:= w_0} + ( \underbrace{
\bold{Σ}^{-1} (\boldsymbol{μ}_1 - \boldsymbol{μ}_2)
}_{:= \bold{w}} )^\top \bold{x}
) \\
& = σ( w_0 + \bold{w}^\top \bold{x} )
\end{align*}
複数クラスでも同様に求められる。
\begin{align*}
p(\mathcal{C}_c|\bold{x}) & = \text{Softmax}(\begin{bmatrix}
a_1 (\bold{x}) \\
\vdots \\
a_c (\bold{x}) \\
\end{bmatrix}) \\
a_c (\bold{x}) & =
\underbrace{
-\frac{1}{2} \boldsymbol{μ}_c^\top \bold{Σ}^{-1} \boldsymbol{μ}_c + \ln p(\mathcal{C}_c)
}_{:= w_{c,0}} + ( \underbrace{
\bold{Σ}^{-1} \boldsymbol{μ}_c
}_{:= \bold{w}_c} )^\top \bold{x}
\end{align*}
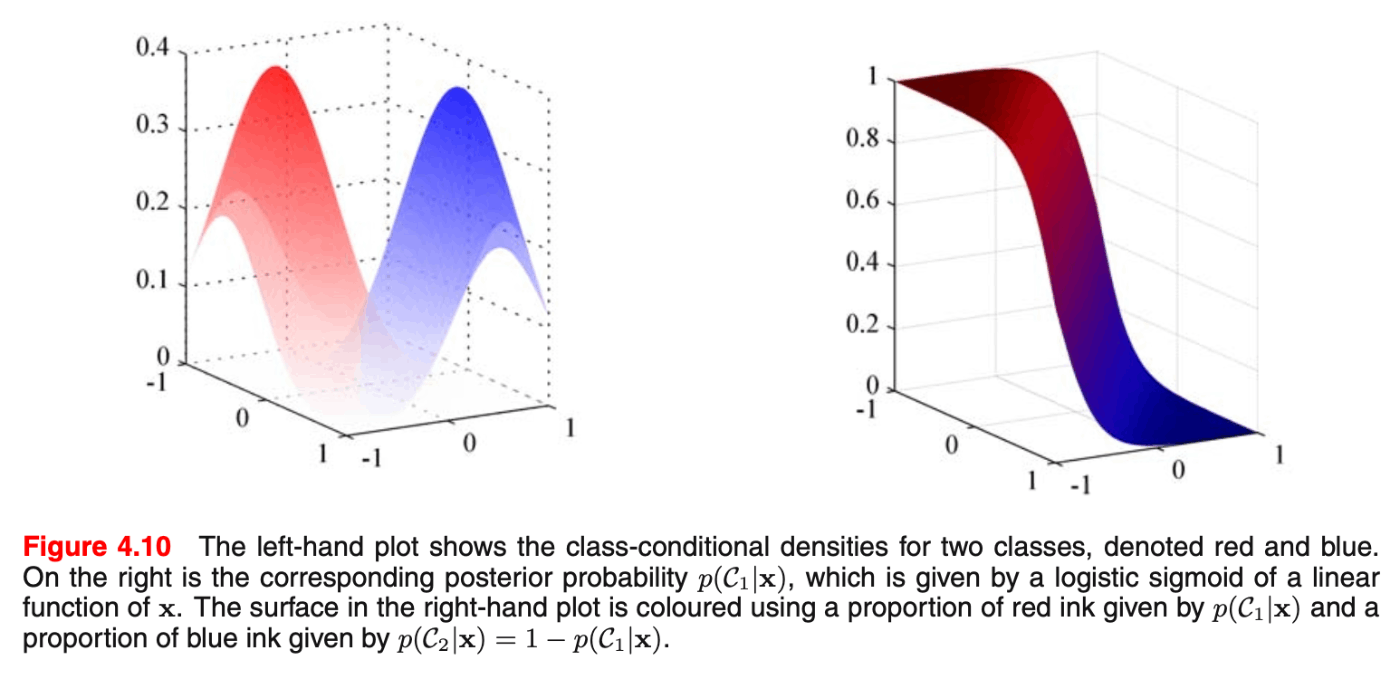PRMLより、各クラスのクラス内分布(条件付き確率密度)と、それに対する事後確率分布
以上により、確率的生成モデルの考え方での分類モデルを定義することができた。
モデルの最適化
次は、学習データとして \bold{X} と対応するラベル \bold{t} \in \{1(\mathcal{C}_1),0(\mathcal{C}_2)\} がある場合の、2クラス分類の最尤推定によるパラメータ \boldsymbol{μ}, \bold{Σ} の決定について見ていく。
事前分布 p(\mathcal{C}_1) = r 、2値分類なので自動的に p(\mathcal{C}_2) = 1-r を仮定する。このとき、尤度は次のように書ける。
\begin{align*}
p(\bold{x}_n,\mathcal{C}_1) & = p(\mathcal{C}_1)p(\bold{x}_n|\mathcal{C}_1) \\
& = r \mathcal{N}(\bold{x}_n| \boldsymbol{μ}_1, \bold{Σ}) \\
p(\bold{x}_n,\mathcal{C}_2) & = p(\mathcal{C}_2)p(\bold{x}_n|\mathcal{C}_2) \\
& = (1-r) \mathcal{N}(\bold{x}_n| \boldsymbol{μ}_2, \bold{Σ}) \\
\end{align*}
\begin{align*}
p(\bold{X},\bold{t}|\bold{r},\boldsymbol{μ}_1,\boldsymbol{μ}_2,\bold{Σ}) & = \prod_{n=1}^N \begin{cases}
p(\bold{x}_n,\mathcal{C}_1) & : t_n = 1 \\
p(\bold{x}_n,\mathcal{C}_2) & : t_n = 0 \\
\end{cases} \\
& = \prod_{n=1}^N (r \mathcal{N}(\bold{x}_n| \boldsymbol{μ}_1, \bold{Σ}))^t ((1-r) \mathcal{N}(\bold{x}_n| \boldsymbol{μ}_2, \bold{Σ}))^{1-t} \\
\ln p(\bold{X},\bold{t}|\bold{r},\boldsymbol{μ}_1,\boldsymbol{μ}_2,\bold{Σ}) & = \sum_{n=1}^N (t_n \ln r + (1-t_n) \ln (1-r))
\end{align*}
まずクラスの確率 r について見てみる。
最大値の条件より \frac{∂}{∂\bold{r}} \ln p(\bold{X},\bold{t}|\bold{r},\boldsymbol{μ}_1,\boldsymbol{μ}_2,\bold{Σ}) = 0 を計算して整理すると、クラスの確率 p(\mathcal{C}_1) がクラスに属するデータ数の割合に一致することが示される。これは感覚的にも自然である。
r = \frac{1}{N} \sum_{n=1}^N t_n = \frac{N_1}{N_1+N_2}
次は \boldsymbol{μ} について見てみる。
同様に最大値の条件を計算すると、所属するクラスに対応した入力変数 \bold{x}_n の平均がそれぞれのクラスの平均になっている。
\begin{align*}
\boldsymbol{μ}_1 & = \frac{1}{N_1} \sum_{n=1}^N t_n \bold{x}_n & = \frac{1}{N_1} \sum_{n \in \mathcal{C}_1} \bold{x}_n \\
\boldsymbol{μ}_2 & = \frac{1}{N_2} \sum_{n=1}^N (1-t_n) \bold{x}_n & = \frac{1}{N_2} \sum_{n \in \mathcal{C}_2} \bold{x}_n \\
\end{align*}
最後に共分散行列 \bold{Σ} について見てみる。
PRML(4.77)からどう変形すれば求まるか理解できなかったので謎は残るが、結果だけ示すと \bold{Σ} の最尤解はクラスに属するデータ数の割合で重み付けされた各共分散の和に等しくなるらしい。これは面白い。
\bold{Σ} = \frac{N_1}{N} \underbrace{
\frac{1}{N_1} \sum_{n \in \mathcal{C}_1} (\bold{x}_n - \boldsymbol{μ}_1)(\bold{x}_n - \boldsymbol{μ}_1)^\top
}_{:=\bold{Σ}_1} + \frac{N_2}{N} \underbrace{
\frac{1}{N_2} \sum_{n \in \mathcal{C}_2} (\bold{x}_n - \boldsymbol{μ}_2)(\bold{x}_n - \boldsymbol{μ}_2)^\top
}_{:=\bold{Σ}_2}
以上により、確率的生成モデルによる分類の最尤推定について理解できた。
ガウス分布の最尤推定は過学習が起きるので、尤度 p(\bold{X},\bold{t}|\bold{r},\boldsymbol{μ}_1,\boldsymbol{μ}_2,\bold{Σ}) に加えて事前分布 p(\bold{r},\boldsymbol{μ}_1,\boldsymbol{μ}_2,\bold{Σ}) を設計してMAP推定することでより頑健なモデルになる。
さらに、特徴次元がクラス \mathcal{C}_c に対して条件付き独立であるという設定を課す ナイーブベイズ(Naive Bayes) 分類器は有名。
2. 確率的識別モデルとロジスティック回帰
前述の方法は、クラスの条件付き分布と事前分布を別々にfitすることで一般化線形モデルのパラメータを決定する。この方法は求めたパラメータを使って周辺分布 p(\bold{x}) を描けるので、人工的にデータ \bold{x} を生成できる。したがって 生成モデル(generative model) と呼ばれる。
一方、クラスの条件付き分布で定義できる尤度を最大化することで、求めるパラメータを少なくし、さらにクラスの条件付き分布がデータの分布を正確に反映できていない場合も比較的うまくいく分類モデルを考えることもできる。これは 識別モデル(discriminative model) と呼ばれる。ロジスティック回帰など、確率分布を作るのではなく決定境界を定めるタイプのモデルはこっちである。
ロジスティック回帰モデルの設定
まず2クラス分類のロジスティック回帰モデルを考える。
入力は基底関数 φ(\bold{x}_n) \in \mathbb{R}^D で予め線形分離可能なものに飛ばしているものと仮定し、それを \bold{x}_n に置き換えて書くことにする。
確率的生成モデルの章で示した通り、クラスの条件付き確率 p(\mathcal{C}_1|\bold{x}) は \bold{x} の線形関数のシグモイドとして書けた。
p(\mathcal{C}_1|\bold{x}) = y(\bold{x},\bold{w}) = σ(\bold{w}^\top \bold{x})
学習データとして \bold{X} と対応するラベル \bold{t} \in \{1(\mathcal{C}_1),0(\mathcal{C}_2)\} がある場合、尤度は次のように書けて、負の対数尤度は クロスエントロピー(cross-entropy)誤差として有名だ。
\begin{align*}
p(\bold{X},\bold{t}|\bold{w}) & = \prod_{n=1}^N σ(\bold{w}^\top\bold{x}_n)^{t_n} (1-σ(\bold{w}^\top\bold{x}_n))^{1-t_n} \\
- \ln p(\bold{X},\bold{t}|\bold{w}) & = \underbrace{
- \sum_{n=1}^N (t_n \ln σ(\bold{w}^\top \bold{x}_n) + (1-t_n)\ln(1-σ(\bold{w}^\top \bold{x}_n)))
}_{:= E(\bold{w})} \\
\frac{∂E(\bold{w})}{∂\bold{w}} & = -\sum_{n=1}^N (t_n - σ(\bold{w}^\top \bold{x}_n)) \bold{x}_n
\end{align*}
見て分かる通り、誤差関数 E(\bold{w}) は \text{Cross-Entropy}([σ(\bold{w}^\top\bold{x}_n)]_{n=1}^{N}) となっている。さらに、その勾配は y(\bold{x},\bold{w}) = σ(\bold{w}^\top \bold{x}) の読み替えをすれば線形回帰における二乗和誤差の勾配と同じである。したがってMAP推定により正則化項をつける方法などは通常の線形回帰と大差なく行える。
ただし、誤差関数に含まれる y(\bold{x},\bold{w}) は、線形回帰では \bold{w}^\top\bold{x} だがロジスティック回帰では σ(\bold{w}^\top \bold{x}) であり、これでは解析的に導出できないことに注意。
次に複数クラスのロジスティック回帰を考える。
学習データとして \bold{X} と対応するクラスのone-hotラベル \bold{T} = [\bold{t}_n \in \{1,0\}^C]_{n=1}^{N} \in \{1,0\}^{N×C} がある場合、パラメータ \bold{W} = [\bold{w}_c \in \mathbb{R}^D]_{c=1}^C \in \mathbb{R}^{C×D} を使って、クラスの条件付き確率と尤度は次のように表される。
\begin{align*}
p(\mathcal{C}_c|\bold{x}) & = y_c(\bold{x},\bold{w}) = \text{Softmax}_c(\bold{w}_c^\top\bold{x}) \\
p(\bold{X}, \bold{T}|\bold{W}) & = \prod_{n=1}^N \prod_{c=1}^C p(\mathcal{C}_c|\bold{x}_n)^{t_{n,c}} \\
& = \prod_{n=1}^N \prod_{c=1}^C \text{Softmax}_c(\bold{w}_c^\top\bold{x}_n)^{t_{n,c}} \\
- \ln p(\bold{X}, \bold{T}|\bold{W}) & = \underbrace{
- \sum_{n=1}^N \sum_{c=1}^C t_{n,c} \ln \text{Softmax}_c(\bold{w}_c^\top\bold{x}_n)
}_{:= E(\bold{W})} \\
\end{align*}
これも(当然ながら)誤差関数がクロスエントロピーになっている。
プロビット回帰
ロジスティック回帰と似た分類モデルとしてプロビット回帰がある。
プロビット回帰の活性化関数は、シグモイドの代わりに累積分布関数を用いる。
p(\mathcal{C}_1|\bold{x}) = y(\bold{x},\bold{w}) = \underbrace{\int_{-∞}^{\bold{w}^\top\bold{x}} p(θ) dθ}_{:=f(\bold{w}^\top\bold{x})}
特に p(θ) = \mathcal{N}(θ|0,1) のとき、これを逆プロビット関数と呼び、殆どシグモイドと同じ形の関数だが、シグモイドが e^{-x} で減衰するのに対して逆プロビットは e^{-x^2} で減衰するので、プロビットモデルの方が外れ値に敏感になる。
より拡張した話として一般化線形モデルの分類モデルを考えるとき、指数分布族(PRML2.4 正規分布などの属する、ナチュラルパラメータ η とスケールパラメータ s で標準的に書き下せる分布)を使うと、誤差関数の勾配は次のように書ける。
\frac{∂}{∂\bold{w}}E(\bold{w}) \frac{1}{s} \sum_{n=1}^N (y(\bold{w},\bold{x}_n) - \bold{t}_n) \bold{x}_n
尤度がガウス分布なら s=β^{-1} 、ロジスティックモデルなら s=1 となる。
IRLSによる最適化
ロジスティック回帰の誤差関数は閉じた最尤解を得られない。
そこで IRLS(itrative reweighting least squares) を使うことで、パラメータ更新により最適化を行う。
ニュートンラフソン法: 関数の局所二次近似を用いて反復的に最適化する方法。今回扱う誤差関数はクロスエントロピーであり、これは凸で唯一の最小解を持つことが保証され、以下の反復式で最小化を行える。
\bold{w}^{\text{new}} = \bold{w}^{\text{old}} - \bold{H}^{-1} \frac{∂}{∂\bold{w}} E(\bold{w})
\bold{H} は誤差関数の2階微分によるヘッセ行列。
例えば、単純な線形回帰の二乗和誤差の最小化をこれで行うと、次のようになり最適解と一致する。
\begin{align*}
E(\bold{w}) & = \frac{1}{2} \sum_{n=1}^N (\bold{w}^\top\bold{x}_n)^2 \\
\frac{∂}{∂\bold{w}} E(\bold{w}) & = \sum_{n=1}^N (\bold{w}^\top\bold{x}_n - t_n) \bold{x}_n \\
& = \bold{X}^\top\bold{X}\bold{w} - \bold{X}^\top\bold{t} \\
\bold{H} = \frac{∂^2}{∂\bold{w}^2} E(\bold{w}) & = \sum_{n=1}^N \bold{x}_n^\top\bold{x}_n \\
& = \bold{X}^\top\bold{X}
\end{align*}
\begin{align*}
\bold{w}^{\text{new}} & = \bold{w}^{\text{old}} - (\bold{X}^\top\bold{X})^{-1} (\bold{X}^\top\bold{X}\bold{w}^{\text{old}} - \bold{X}^\top\bold{t}) \\
& = (\bold{X}^\top\bold{X})^{-1} \bold{X}^\top\bold{t}
\end{align*}
この方法を2クラス分類ロジスティック回帰のクロスエントロピー誤差に適用する。
\begin{align*}
E(\bold{w}) & = - \sum_{n=1}^N (t_n \ln σ(\bold{w}^\top \bold{x}_n) + (1-t_n)\ln(1-σ(\bold{w}^\top \bold{x}_n))) \\
\frac{∂}{∂\bold{w}} E(\bold{w}) & = - \sum_{n=1}^N (t_n - σ(\bold{w}^\top \bold{x}_n)) \bold{x}_n \\
& = \bold{X}^\top ( \underbrace{ \begin{bmatrix}
σ(\bold{w}^\top \bold{x}_1) \\
\vdots \\
σ(\bold{w}^\top \bold{x}_N) \\
\end{bmatrix} }_{:= \bold{y}} - \bold{t} ) \\
\bold{H} = \frac{∂^2}{∂\bold{w}^2} E(\bold{w}) & = \sum_{n=1}^N σ(\bold{w}^\top \bold{x}_n) (1 - σ(\bold{w}^\top \bold{x}_n)) \bold{x}_n \bold{x}_n^\top \\
& = \bold{X}^\top \underbrace{ \begin{bmatrix}
σ(\bold{w}^\top \bold{x}_1) (1 - σ(\bold{w}^\top \bold{x}_1)) & & \bold{O} \\
& \ddots & \\
\bold{O} & & σ(\bold{w}^\top \bold{x}_N) (1 - σ(\bold{w}^\top \bold{x}_N)) \\
\end{bmatrix} }_{:= \bold{R}} \bold{X}
\end{align*}
\begin{align*}
\bold{w}^{\text{new}} & = \bold{w}^{\text{old}} - (\bold{X}^\top\bold{R}\bold{X})^{-1} \bold{X}^\top (\bold{y} - \bold{t}) \\
& = (\bold{X}^\top\bold{R}\bold{X})^{-1} (\bold{X}^\top\bold{R}\bold{X}\bold{w}^{\text{old}} - \bold{X}^\top (\bold{y} - \bold{t})) \\
& = (\bold{X}^\top\bold{R}\bold{X})^{-1} \bold{X}^\top\bold{R} \underbrace{ (\bold{X}\bold{w}^{\text{old}} - \bold{R}^{-1}(\bold{y} - \bold{t})) }_{:= \bold{z}}
\end{align*}
この式は \bold{X}, \bold{z} に注目したときのIRLSの正規方程式になっており、 \bold{R} は分散の意味を持つ。
\bold{R} は \bold{w} を含んでいるので反復のたびに計算し直す必要がある。
また、複数クラスのクロスエントロピー誤差については次のものに置き換えることで導ける。
\begin{align*}
\frac{∂}{∂\bold{w}_c}E(\bold{W}) & = \sum_{n=1}^N (\text{Softmax}_c(\bold{w}_c^\top\bold{x}_n) - t_{n,c}) \bold{x}_n \\
\frac{∂}{∂\bold{w}_{c_1}}\frac{∂}{∂\bold{w}_{c_2}}E(\bold{W}) & = \sum_{n=1}^N \text{Softmax}_{c_1}(\bold{w}_{c_1}^\top\bold{x}_n)(I_{c_1,c_2} - \text{Softmax}_{c_2}(\bold{w}_{c_2}^\top\bold{x}_n)) \bold{x}_n \bold{x}_n^\top \\
\end{align*}
以上により、ロジスティック回帰に出てくるクロスエントロピー誤差を最小化するパラメータを求める方法がわかった。
3. Lassoロジスティック回帰
2クラス分類のロジスティック回帰の最尤推定とLassoの事前分布を思い出すと、「 \bold{w} が0付近に密集するだろう」という信念を与えた事後分布を最大化する(つまりMAP推定)ことで、ロジスティック回帰のLasso版が導出できる。
\begin{align*}
p(\bold{w}|λ) & = \prod_{d=1}^D \text{Laplace}(\bold{w}_d|0, λ^{-1}) \\
p(\bold{X},\bold{t}|\bold{w}) & = \prod_{n=1}^N σ(\bold{w}^\top\bold{x}_n)^{t_n} (1-σ(\bold{w}^\top\bold{x}_n))^{1-t_n} \\
p(\bold{w}|\bold{X},\bold{t},λ) & ∝ p(\bold{X},\bold{t}|\bold{w})p(\bold{w}|λ) \\
& = \prod_{n=1}^N σ(\bold{w}^\top\bold{x}_n)^{t_n} (1-σ(\bold{w}^\top\bold{x}_n))^{1-t_n} \prod_{d=1}^D \frac{λ}{2} e^{-λ|w_d|} \\
- \frac{∂}{∂\bold{w}} \ln p(\bold{X},\bold{t}|\bold{w}) & = \frac{∂}{∂\bold{w}} (- \sum_{n=1}^N (t_n \ln σ(\bold{w}^\top \bold{x}_n) + (1-t_n)\ln(1-σ(\bold{w}^\top \bold{x}_n))) + λ \underbrace{\sum_{d=1}^D |w_d|}_{= ||\bold{w}||_{\text{L1}}} ) \\
\end{align*}
誤差関数にL1正則化項が出てきた。
最後に、この最適化をIRLSのループに組み込むことでMAP解を計算する。もともとの最尤解の反復式に現れる変数と計算を使って、Lassoの反復計算に置き換える。このLassoの式はCholesky分解を用いる一般化の形であることが思い出せる。
\begin{align*}
\bold{w}_{\text{ML}}^{\text{new}} & = (\bold{X}^\top\bold{R}\bold{X})^{-1} \bold{X}^\top\bold{R} \underbrace{ (\bold{X}\bold{w}^{\text{old}} - \bold{R}^{-1}(\bold{y} - \bold{t})) }_{:= \bold{z}} \\
\bold{w}_{\text{Lasso}}^{\text{new}} & = \min_{\bold{w}}( (\bold{z}-\bold{X}\bold{w}^{\text{old}})^\top \bold{R} (\bold{z}-\bold{X}\bold{w}^{\text{old}}) + λ ||\bold{w}^{\text{old}}||_{\text{L1}})
\end{align*}
具体的には、まず分散行列 \bold{R} の対角成分である σ(\bold{x}_n^\top\bold{w})(1- σ(\bold{x}_n^\top\bold{w})) を計算し、それを使って \bold{z} を計算する。これにより線形回帰のLassoの最小化と同じ操作が可能になる。
要するに、ロジスティック回帰によって現れた変数を行列計算によってシンプルな線形回帰Lassoの入力に置き換えることができるということである。あとは通常のLassoのソルバーで解けばパラメータが求まるようになる。
以上によりLassoロジスティック回帰のパラメータが最適化できる。
感想
ベイジアンロジスティック回帰の使用(PyMC)は以下の記事で行った。
https://zenn.dev/inaturam/articles/9d2844296a89cc
PRMLを読みつつSEwPを眺めてみた。
SEwPは計算の実装が具体的に載っているため、頭の中で処理がイメージできる点は邦訳の本で唯一性があり最高なのだが、正直なところ計算の見通しが悪くて教科書としてはあまりおすすめできない...
おそらく、わかっている人からすると当然のことが書いてあるが、初学者が読むと「急に誤差関数が与えられた(ベイズ的には自然)」「急に見慣れない行列が挟まった式が与えられた(マハラノビス距離から導けばCholesky分解のために必要なのが見える)」みたいな具合で、行間や目的を補完しながら読まないと難しいので、勉強不足の人が読むには厳しい。
次は一般化線形モデルの続きを読み勧めていきたい。
Discussion