🍙
Balanced Truncation法による複素指数関数和のモデル縮約

2025/07/19に公開
 概要前回のESPRIT法に関する記事では、関数あるいは等間隔時系列データを複素指数関数和で近似する方法について解説した。

一方で本稿では、すでに得られている指数関数和に対して、システム制御理論におけるモデル縮約（Model Order Reduction）手法であるBalanced Truncation法[1][2]を適用し、関数の項数を削減する手法を紹介する。まずアルゴリズムを概観し、続いて実装例を示す。

 アルゴリズムの導入以下のアルゴリズムは、論文[2:1]を参照した。
まず、複素指数関数和

f(t) = \sum_{k=1}^M c_k \mathrm{e}^{-a_k t}, \quad c_k,a_k\in\mathbb{C},\; \operatorname{Re}(a_k)>0.
がすでに与えられているとする。本手法の目的は、ある精度 \delta に対して、より少ない項数 M'\leq M を持つ別の指数和を用いて f(t) を近似することであり、すなわち

g(t)=\sum_{k=1}^{M'} c_k' \mathrm{e}^{-a_k' t}, 
\quad
\left\|f(t)-g(t)\right\| < \delta 
が成り立つような g(t) を考える。
f(t) をラプラス変換すると、

f(s) 
= \mathcal{L}\bigl[f(t)\bigr] 
= \int_{0}^\infty \mathrm{d}t\, f(t) \, \mathrm{e}^{-st} 
= \sum_{k=1}^{M} \frac{c_k}{s+a_k}
となる。すると問題は、高次の有理関数を低次の有理関数で近似する最適化問題に帰着し、

g(s)
= \mathcal{L}\bigl[g(t)\bigr] = \sum_{k=1}^{M'} \frac{c_k'}{s+a_k'}, 
\quad
\left\|f(s)-g(s)\right\| < \epsilon
と定式化できる。これはすべての s > 0 について成立する。
次にc_k,a_k を用いて、可制御性グラミアン \mathbf{W}_\mathrm{c} \in \mathbb{C}^{M\times M} を構成する。これは

[\mathbf{W}_\mathrm{c}]_{ij} = \frac{\sqrt{c_i c_j^*}}{a_i + a_j^*}
で与えられる。このようにして得られる \mathbf{W}_\mathrm{c} は自己随伴準コーシー行列であり、con-eigenvalue分解

\mathbf{W}_\mathrm{c} 
= \bar{\mathbf{U}} \,\boldsymbol{\Sigma}\, \mathbf{U}^{T}
をもつ。ここで、\mathbf{U} \in \mathbb{C}^{M\times M} はユニタリ行列、\bar{\mathbf{U}}はその複素共役、\boldsymbol{\Sigma} = \mathrm{diag}(\sigma_1,\dots,\sigma_M) は \sigma_1 \ge \sigma_2 \ge \cdots \ge \sigma_M > 0 をみたす対角行列となる。 アルゴリズム等の詳細は論文[3]を参照をされたい。
整数 M' を与えられた精度 \epsilon に対して

2\sum_{i=M'+1}^{M} \sigma_i \leq \epsilon
をみたすように選び、次式によって縮約モデルを構成する。

\mathbf{A}' = \mathbf{U}_{M'}^{*}\,\mathbf{A}\,\bar{\mathbf{U}}_{M'} \in \mathbb{C}^{M'\times M'}, \quad \mathbf{b}' = \mathbf{U}_{M'}\,\mathbf{b} \in \mathbb{C}^{M'},
ここで、\mathbf{A} = \operatorname{diag}(a_1, a_2, \ldots, a_M)、\mathbf{b} = (\sqrt{c_1}, \sqrt{c_2}, \ldots, \sqrt{c_M})^T、 \mathbf{U}_{M'} = \mathbf{U}(1\!:\!M,\,1\!:\!M') である。
最後に、\mathbf{A}' の固有値分解

\mathbf{A}' = \mathbf{X} \,\boldsymbol{\Lambda}\,\mathbf{X}^{-1}
を計算すると、縮約されたパラメータ

a_{i}'=\boldsymbol{\Lambda}_{ii}, 
\quad
c_i'=((\mathbf{X}^{-1}\mathbf{b}')_i)^{2} 
\quad
(i=1, \ldots, M')
が得られる。

 ソースコードC++実装は

https://github.com/hydeik/mxpfit

で公開されている。
また筆者によって

https://github.com/DOC-Package/ExpFit.jl

Juliaでも実装されている。
ここではExpFit.jlを使ってみる。例として、乱数で生成した M=200 個の複素パラメータ \{(c_k,a_k)\} をもつ関数を近似することを考える。精度は \epsilon = 1.0\times 10^{-3} とした。以下コードを示す。
using LinearAlgebra
using ExpFit
using Random
using LaTeXStrings 

function generate_exponent_coefficient_pairs(n::Int)
    Random.seed!(123)
    exponents = Vector{ComplexF64}(undef, n)
    coefficients = Vector{ComplexF64}(undef, n)
    for i in 1:n
        re_exp = rand() * 9.9 + 0.1
        im_exp = randn()  
        exponents[i] = re_exp + im_exp*im
        re_coeff = randn()
        im_coeff = randn()
        coefficients[i] = re_coeff + im_coeff*im
    end
    return exponents, coefficients
end

tmin = 0.0
tmax  = 20.0      
eps = 1e-3
N = 200
t = range(tmin, tmax, length=N)

# 近似する指数関数の生成
a, c = generate_exponent_coefficient_pairs(200)
f = Exponentials(a,c)

# Balanced Truncation法による近似
er = expred(a, c, eps)
print("Approximation order = ", length(er.coeff), "\n")

# 近似値と誤差の計算
fv = f.(t)
erv = er.(t)
err = abs.(erv .- fv)
与えた精度に対して、次数は M'=14 となった。以下に結果を図示した。
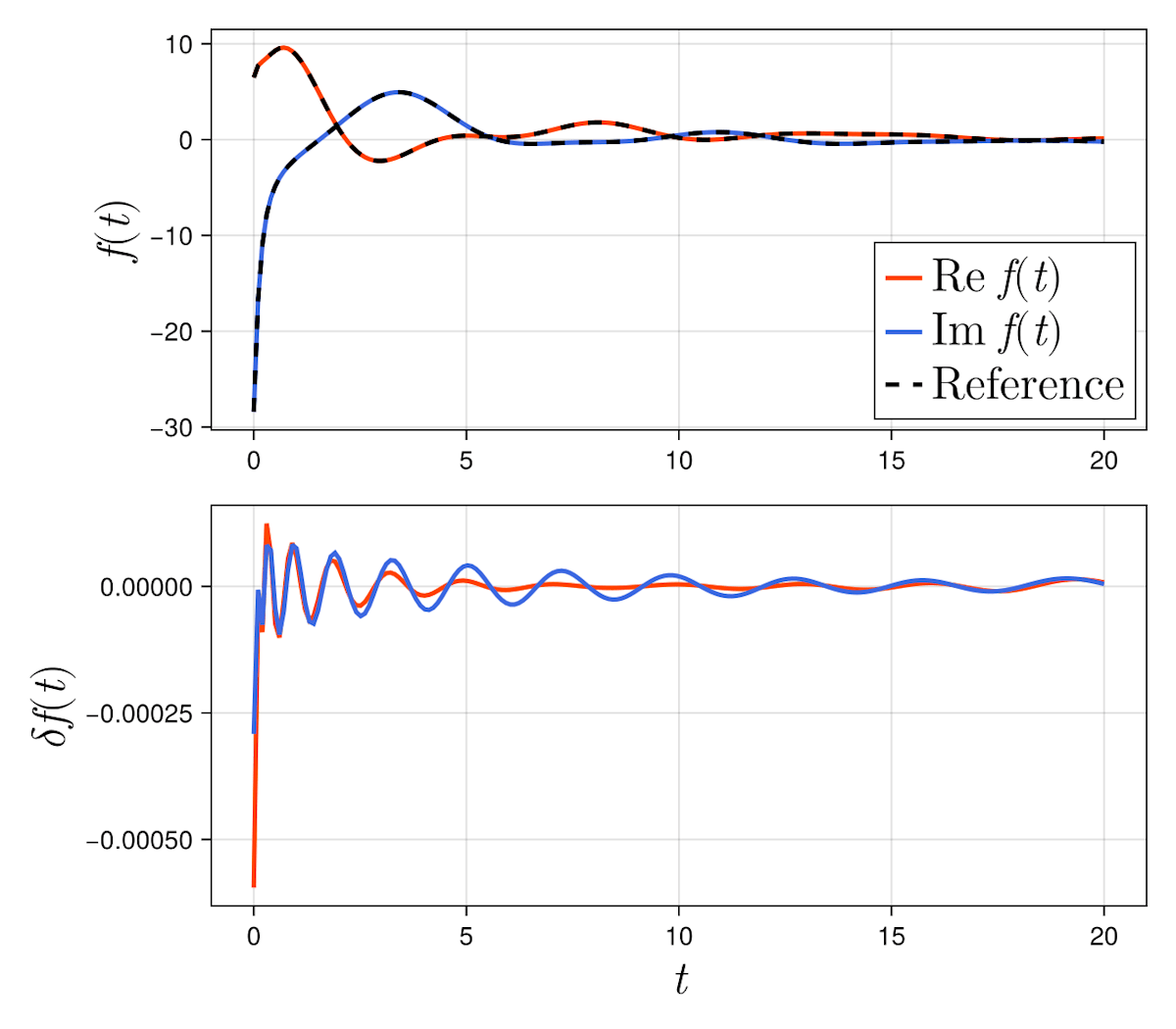
誤差が与えた精度内に収まっており、よく近似できていることが確認できる。

脚注
B. Moore, IEEE Trans. Autom. Control 26, 17–32 (1981). ↩︎
H. Ikeno, Comput. Phys. Commun. 230, 135–144 (2018). ↩︎ ↩︎
T. Haut and G. Beylkin, SIAM J. Matrix Anal. Appl. 33, 1101–1125 (2012). ↩︎
GitHubで編集を提案
概要

アルゴリズムの導入

ソースコード

Discussion
