複素指数関数和近似：ESPRIT法

概要

本稿では、信号処理分野における周波数推定の効率的なアルゴリズムのひとつであるESPRIT法^[1][2]を紹介する。類似の手法として、Prony法^[3]やMatrix Pencil法^[4]などがあり、これらの手法に関しては文献^[2:1][5]を参考にされたい。またここでは実際の信号への応用よりも、関数を指数関数和で近似することを主眼とする。アルゴリズムを簡単に紹介した後、具体例を示す。

アルゴリズムの導入

問題設定

与えられた関数 $f:\mathbb{R}\to\mathbb{C},\;t \to f(t)$ に対して $f_j=f\left(t_j\right)$ としたとき、ベクトル $\mathbf{f}=\left(f_0, f_1, \ldots, f_{2N-1}\right)^T$ を考える。各要素 $f_j$ は等間隔格子 $t_j=h j,\left(h=\frac{t_c}{2N-1}, \quad j=0,1, \ldots, N^{\prime}\right)$ 上でサンプリングされており、$t_c$ はカットオフ時間、 $2N-1$ はサンプルサイズである。

ここで $f_j$ が以下のように表現できると仮定する。

$$f_j=\sum_{k=1}^M c_k e^{-a_k h j}=\sum_{k=1}^M c_k z_k^j,\quad c_k \in \mathbb{C},\; z_k=e^{-a_k h} \in \mathbb{D}$$

ここで記号 $\mathbb{D}$ は零点を除いた複素単位円板を表す。したがって、問題は与えられた精度 $\varepsilon$ に対して、不等式

$$\left\|f_j-\sum_{k=1}^M c_k z_k^j\right\|<\varepsilon$$

がすべての $j=1, \ldots, N^{\prime}$ について成り立つような、複素重み $\boldsymbol{c}=\left(c_1, \ldots, c_M\right)^T$ と複素ノード $z=\left(z_1, \ldots, z_M\right)^T$ を、項数 $M$ を最小にするように求める問題に帰着する。

指数の評価：Hankel行列とその特異値分解

ESPRIT法は、Hankel行列

$$\mathbf{H}_{2 N-L, L+1}=\left(\begin{array}{cccc} f_0 & f_1 & \cdots & f_L \\ f_1 & f_2 & \cdots & f_N \\ \vdots & \vdots & \ddots & \vdots \\ f_{2 N-L-1} & f_{2 N-L} & \cdots & f_{2 N-1} \end{array}\right)$$

の特異値分解

$$\mathbf{H}_{2 N-L, L+1}=\mathbf{U}_{2 N-L} \Sigma_{2 N-L, L+1} \mathbf{W}_{L+1},$$

を用いる。先に挙げた他手法もHankel行列のランク削減に基づいている。ここで、$\Sigma_{2 N-L, L+1}$ は対角成分が $\sigma_1 \geq \sigma_2 \cdots \geq \sigma_{L+1} \geq 0$ である矩形対角行列である。項数 $M$ は $\sigma_M / \sigma_0<\varepsilon$ という条件を満たすように選ぶ。

すると、ノード $z_k$ は行列 $\mathbf{A}_M$

$$\mathbf{A}_M=\left(\mathbf{W}_M(0)^{\mathrm{T}}\right)^{+} \mathbf{W}_M(1),$$

の固有値として求ることができる。ここで、

$$\mathbf{W}_{M, L}(s)=\mathbf{W}(1: M, 1+s: L+s) \quad(s=0,1)$$

である。$\left(\mathbf{W}_M(0)^{\mathrm{T}}\right)^{+}$ は $\mathbf{W}_M(0)^{\mathrm{T}}$ のMoore-Penrose逆行列を表す。 最後に、指数 $a_k$ はノード $z_k$ から以下のように復元できる。

$$a_k=-\frac{\log \left(z_k\right)}{h} \quad(k=1, \ldots, M)$$

ここで、logは対数の主値である。

係数の評価：過剰決定最小二乗Vandermonde系

係数 $c_k\;(k=1, \ldots, M)$ は、過剰決定最小二乗Vandermonde系を解くことによって得られ、これは矩形Vandermonde行列 $\mathbf{V}_{N^{\prime}, M}$ を用いて

$$\mathbf{V}_{N^{\prime}, M}(\mathbf{z}) \mathbf{c}=\mathbf{f}$$

のように表現される。ここで、$\mathbf{c}=\left(c_1, \ldots, c_M\right)^T$ であり、

$$\mathbf{V}_{N^{\prime}, M}(\mathbf{z})=\left(\begin{array}{cccc} 1 & 1 & \cdots & 1 \\ z_1 & z_2 & \cdots & z_M \\ z_1^2 & z_2^2 & \cdots & z_M^2 \\ \vdots & \vdots & \ddots & \vdots \\ z_1^{N^{\prime}} & z_2^{N^{\prime}} & \cdots & z_M^{N^{\prime}} \end{array}\right)$$

である。

ソースコード

筆者によって実装されたJuliaコードを
https://github.com/DOC-Package/ExpFit.jl
で見つけることができる。その他Prony法、Matrix Pencil法等も実装済みである。^[6]

ExpFit.jlを使ってみる。例としてベッセル関数の和を考える。カットオフ時間は $t_c=50$ とし、精度は $\epsilon = 1.0\times 10^{-3}$ とした。以下コードを示す。

using LinearAlgebra
using ExpFit
using SpecialFunctions

tmin = 0.0
tmax  = 50.0 
N = 100       
t = range(tmin, tmax, length=N*2)
eps = 1e-3     

# 近似する関数（ベッセル関数の和）
f = t -> besselj(0,t) + besselj(2,t) - 1.0im*(besselj(1,t) + besselj(3,t))

# ESPRITの実行
ef = expfit(f, tmin, tmax, N, eps; alg=ESPRIT())
print("Approximation order = ", length(ef.coeff), "\n")

# 結果
fv = f.(t)
efv = ef.(t)
err = efv .- fv
println("Maximum error = ", maximum(abs.(err)))

出力は

Approximation order = 7
Maximum error = 0.0006106060799602027

となった。与えた精度に対して、次数は $M=7$ が得られた。以下に結果を図示する。

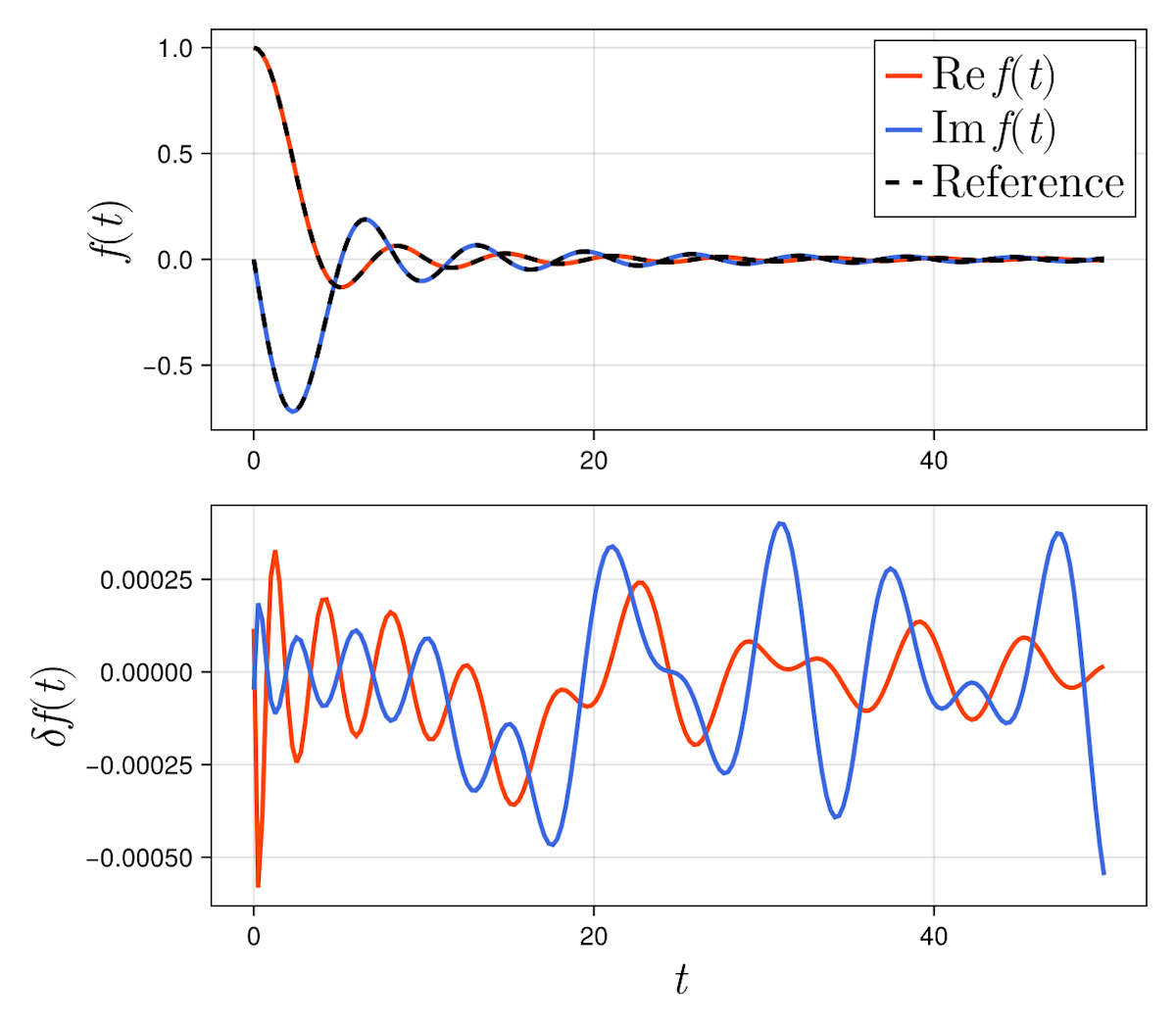
誤差が許容範囲内に収まっており、よく近似できていることが確認できる。

---

脚注

1. R. Roy and T. Kailath, IEEE Trans. Acoust., Speech, Signal Process. 37, 984–995 (1989).

2. D. Potts and M. Tasche, Linear Algebra Appl. 439, 1024–1039 (2013).

3. G. Beylkin and L. Monzón, Appl. Comput. Harmonic Anal. 19, 17–48 (2005).

4. T. Sarkar and O. Pereira, IEEE Antennas Propag. Mag. 37, 48–55 (1995).

5. H. Takahashi, S. Rudge, C. Kaspar, M. Thoss, and R. Borrelli, J. Chem. Phys. 160, 204105 (2024).

6. このソフトウェアは開発中であり、動作の安定性は保証されません。