GaussianProcesses.jlでガウス過程回帰【Julia】
はじめに
前回の記事では Python の GPy を用いてガウス過程回帰をしました。今回は、Julia のパッケージ GaussianProcesses.jl を使ってみます。内容は公式のチュートリアルを基にしています。
パッケージのインストール
ガウス過程回帰と最適化、プロットのパッケージをインストールします。
using Pkg
Pkg.add("GaussianProcesses")
Pkg.add("Optim")
Pkg.add("Plots")
次に、二項分類のサンプルプログラムで使用するパッケージをインストールします。
Pkg.add("RDatasets")
Pkg.add("Distributions")
ガウス過程回帰(1 次元)
パッケージ
using GaussianProcesses
using Plots
using Optim
学習データの作成
前回と同じ関数を使います。
function f(x)
return sin(2π*0.1*x) + sin(2π*0.2*x) + sin(2π*0.3*x)
end
n = 40
x = 20*rand(n) .- 10
y = f.(x) + 0.1*randn(n)
プロットすると次のようになります。
plot(f; xlims=(-12,12), lw=3, legend=false)
scatter!(x, y; ms=5)
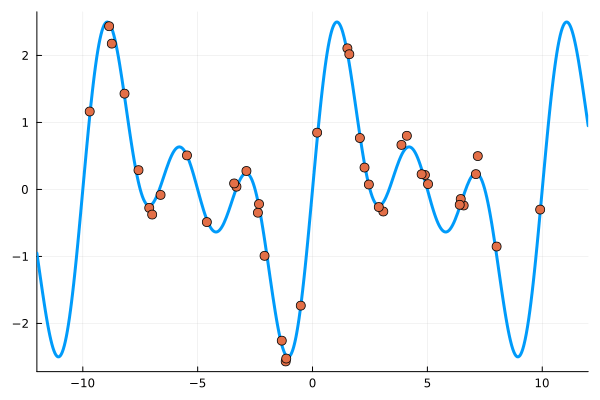
ガウス過程回帰
平均
Julia では SE(ll, lσ) で SE カーネルを使えますが、その引数は対数スケールとなっています。つまり、SE(0.0, 0.0) となっているので、
logObsNoise は観測ノイズの標準偏差の自然対数です。デフォルトは -2.0 で、これは観測ノイズがないと仮定した場合と同じです。また、これはオプションなので省略しても大丈夫です。
mZero = MeanZero()
kern = SE(0.0, 0.0)
logObsNoise = -1.0
gp = GP(x,y,mZero,kern,logObsNoise)
GP Exact object:
Dim = 1
Number of observations = 40
Mean function:
Type: MeanZero, Params: Float64[]
Kernel:
Type: SEIso{Float64}, Params: [0.0, 0.0]
Input observations =
[1.5173535798342908 4.106027667897344 … -7.575769024369823 1.601168105651558]
Output observations = [2.1066035998015145, 0.8009468938266678, -2.567114403987451, -0.2392145675647531, 0.2161880334057395, -0.32937121129135527, -0.08162004711097766, 0.4980496202368598, 0.040960655689881595, 2.436566953472882 … -0.34738884851063834, -0.9910163525657347, 1.1634556248514956, 0.27558085253820175, 0.2274573921663613, -0.30010467468522795, 0.07399667789094777, -2.257150516818323, 0.2883120623174894, 2.018513304664647]
Variance of observation noise = 0.1353352832366127
Marginal Log-Likelihood = -33.49
ガウス過程の結果をプロットします。水色の範囲は 95 % 信頼区間です。
plot(gp; legend=false)

optimize で最適化できます。
optimize!(gp)
* Status: success (objective increased between iterations)
* Candidate solution
Final objective value: 1.809804e+01
* Found with
Algorithm: L-BFGS
* Convergence measures
|x - x'| = 6.08e-10 ≰ 0.0e+00
|x - x'|/|x'| = 2.75e-10 ≰ 0.0e+00
|f(x) - f(x')| = 3.55e-15 ≰ 0.0e+00
|f(x) - f(x')|/|f(x')| = 1.96e-16 ≰ 0.0e+00
|g(x)| = 6.85e-12 ≤ 1.0e-08
* Work counters
Seconds run: 0 (vs limit Inf)
Iterations: 11
f(x) calls: 30
∇f(x) calls: 30
最適化後の結果をプロットすると、最適化前から大きく改善されていることがわかります。
plot(gp; legend=false)
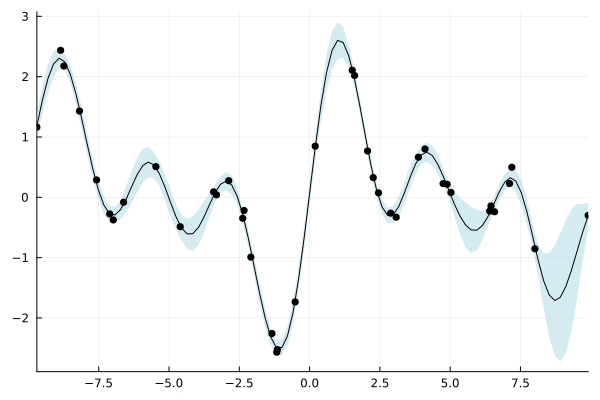
また、β を変えることで信頼区間の幅を変更できます。デフォルトは β=0.95 です。
plot(gp; legend=false, β=0.99)
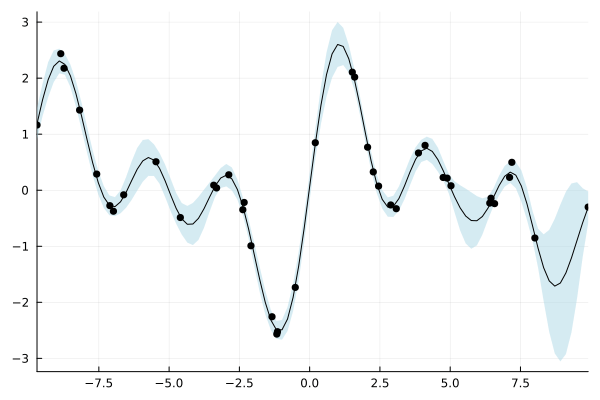
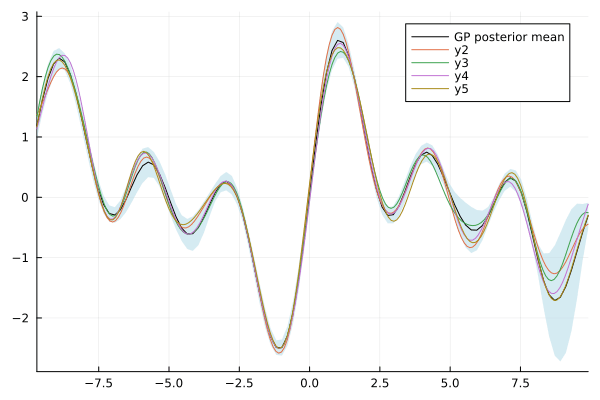
さらに、このガウス過程からサンプリングした結果を重ねることもできます。
x = -12:0.1:12
plot(gp; obsv=false, label="GP posterior mean")
samples = rand(gp, x, 4)
plot!(x, samples)
ガウス過程回帰(2 次元)
学習データの作成
d, n = 2, 50
x = 2π * rand(d, n)
y = sin.(x[1,:]) .* sin.(x[2,:]) + 0.05*rand(n)
ガウス過程回帰
2 次元以上の場合は Iso か ARD が使用可能だそうです。ARD Matern 5/2 kernel は次の式で定義されます。ハイパーパラメータは
今回は、SE カーネルとの複合カーネルを使います。
mZero = MeanZero()
kern = Matern(5/2,[0.0,0.0],0.0) + SE(0.0,0.0)
gp = GP(x,y,mZero,kern)
GP Exact object:
Dim = 2
Number of observations = 50
Mean function:
Type: MeanZero, Params: Float64[]
Kernel:
Type: SumKernel{Mat52Ard{Float64}, SEIso{Float64}}
Type: Mat52Ard{Float64}, Params: [-0.0, -0.0, 0.0] Type: SEIso{Float64}, Params: [0.0, 0.0]
Input observations =
[3.6559218531461783 0.04834230904998851 … 0.47844468192817313 3.1718339541960545; 4.623437835351887 6.156721420798165 … 0.46440801983608004 5.223270245644608]
Output observations = [0.4983616654461181, 0.03989589080449894, 0.6805588386192034, -0.6255644201787386, -0.884627095919968, -0.5677451469547918, -0.8969118937518012, 1.0123123529041695, -0.5492577018565996, -0.1336414181828558 … 0.23575567180902596, -0.1740039666013055, -0.011013454204398546, -0.12011141498717938, -0.3042994814469522, 0.31842572267015534, 0.5620223429117553, 0.328154823059839, 0.24280596142791935, 0.04171333276508114]
Variance of observation noise = 0.01831563888873418
Marginal Log-Likelihood = -29.593
同様に最適化します。
optimize!(gp)
* Status: success (objective increased between iterations)
* Candidate solution
Final objective value: -4.785678e+01
* Found with
Algorithm: L-BFGS
* Convergence measures
|x - x'| = 1.42e-02 ≰ 0.0e+00
|x - x'|/|x'| = 7.16e-04 ≰ 0.0e+00
|f(x) - f(x')| = 3.89e-12 ≰ 0.0e+00
|f(x) - f(x')|/|f(x')| = 8.14e-14 ≰ 0.0e+00
|g(x)| = 2.58e-09 ≤ 1.0e-08
* Work counters
Seconds run: 0 (vs limit Inf)
Iterations: 44
f(x) calls: 145
∇f(x) calls: 145
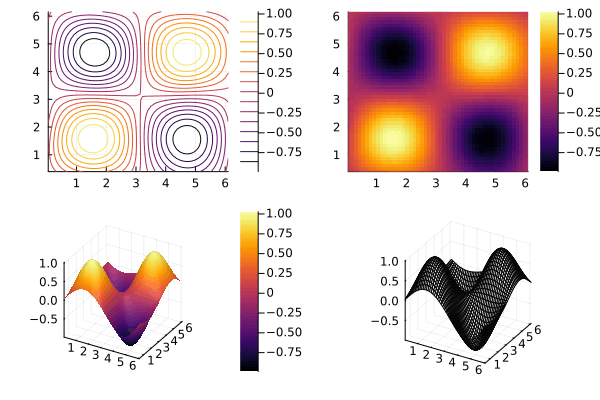
ガウス過程回帰の結果を可視化します。
plot(contour(gp), heatmap(gp), surface(gp), wireframe(gp))
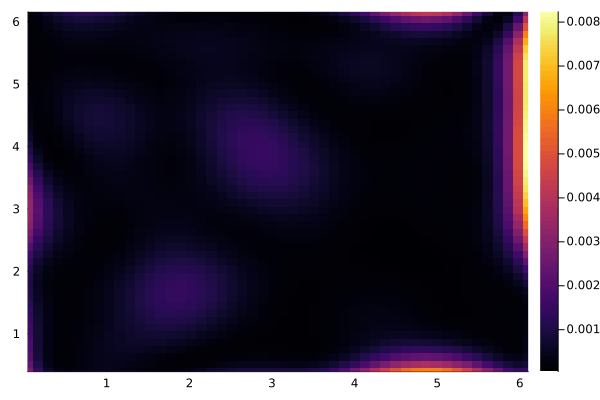
var=true とすることで、分散を可視化できます。
heatmap(gp; var=true)
二項分類
パッケージ
using RDatasets
using Random
import Distributions:Normal
訓練データの作成
今回は crabs データセットを利用し、5 つの変数を用いて Sp が B か O かどうかを分類します。
crabs = dataset("MASS", "crabs")
crabs
200×8 DataFrame
Row │ Sp Sex Index FL RW CL CW BD
│ Cat… Cat… Int32 Float64 Float64 Float64 Float64 Float64
─────┼────────────────────────────────────────────────────────────────
1 │ B M 1 8.1 6.7 16.1 19.0 7.0
2 │ B M 2 8.8 7.7 18.1 20.8 7.4
3 │ B M 3 9.2 7.8 19.0 22.4 7.7
4 │ B M 4 9.6 7.9 20.1 23.1 8.2
5 │ B M 5 9.8 8.0 20.3 23.0 8.2
6 │ B M 6 10.8 9.0 23.0 26.5 9.8
7 │ B M 7 11.1 9.9 23.8 27.1 9.8
8 │ B M 8 11.6 9.1 24.5 28.4 10.4
⋮ │ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ ⋮
194 │ O F 44 20.9 16.5 39.9 44.7 17.5
195 │ O F 45 21.3 18.4 43.8 48.4 20.0
196 │ O F 46 21.4 18.0 41.2 46.2 18.7
197 │ O F 47 21.7 17.1 41.7 47.2 19.6
198 │ O F 48 21.9 17.2 42.6 47.4 19.5
199 │ O F 49 22.5 17.2 43.0 48.7 19.8
200 │ O F 50 23.1 20.2 46.2 52.5 21.1
185 rows omitted
crabs をシャッフルし、前半を訓練データ、後半をテストデータとします。
crabs = crabs[shuffle(1:size(crabs,1)), :]
train = crabs[1:div(end,2), :]
y = Array{Bool}(undef, size(train,1))
y[train[:,:Sp].=="B"] .= 0
y[train[:,:Sp].=="O"] .= 1
X = Matrix(train[:,4:end])
test = crabs[div(end,2)+1:end, :]
yTest = Array{Bool}(undef, size(test,1))
yTest[test[:,:Sp].=="B"] .= 0
yTest[test[:,:Sp].=="O"] .= 1
xTest = Matrix(test[:,4:end])
ガウス過程回帰
平均
mZero = MeanZero()
kern = Matern(3/2, zeros(5), 0.0)
lik = BernLik()
次にガウス過程回帰をします。今回はガウス分布ではないので近似となります。
gp = GP(X', y, mZero, kern, lik)
GP Approximate object:
Dim = 5
Number of observations = 100
Mean function:
Type: MeanZero, Params: Float64[]
Kernel:
Type: Mat32Ard{Float64}, Params: [-0.0, -0.0, -0.0, -0.0, -0.0, 0.0]
Likelihood:
Type: BernLik, Params: Any[]
Input observations =
[10.8 11.5 … 14.7 15.1; 9.0 11.0 … 12.5 13.3; … ; 26.5 29.2 … 34.7 36.3; 9.8 10.1 … 12.5 13.5]
Output observations = Bool[0, 0, 1, 1, 1, 1, 0, 0, 0, 1 … 1, 1, 0, 0, 0, 1, 1, 0, 0, 0]
Log-posterior = -161.209
ハイパーパラメータに正規分布を設定し、MCMC 法を使います。
set_priors!(gp.kernel, [Normal(0.0,2.0) for i in 1:6])
samples = mcmc(gp; nIter=10000, burn=1000, thin=10)
Number of iterations = 10000, Thinning = 10, Burn-in = 1000
Step size = 0.100000, Average number of leapfrog steps = 10.041600
Number of function calls: 100417
Acceptance rate: 0.108000
ymean = Array{Float64}(undef, size(samples,2), size(xTest,1))
for i in 1:size(samples,2)
set_params!(gp, samples[:,i])
update_target!(gp)
ymean[i,:] = predict_y(gp, xTest')[1]
end
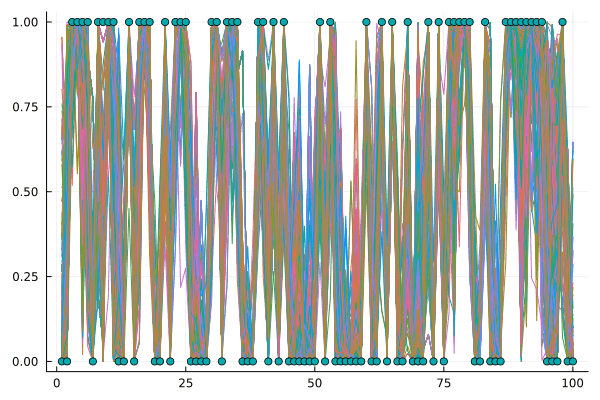
可視化すると次のようになります。
plot(ymean',leg=false)
scatter!(yTest)
Discussion