ガウス過程回帰とGPyのメモ

はじめに

Kindle の日替わりセールで買って積読になっていた『ガウス過程と機械学習』を読んだので，ガウス過程回帰について整理し，GPy で試してみました．この記事の内容は『ガウス過程と機械学習』の 2-4 章に対応しています．

ガウス過程回帰とは回帰分析手法の一種で，非線形な関数関係を表すことができます．ガウス過程回帰ではカーネル関数と呼ばれる類似度を表す関数を設定しますが，このカーネル関数を変えることで無限回微分可能な滑らかな関数やブラウン運動，周期性など様々なものを扱えます．

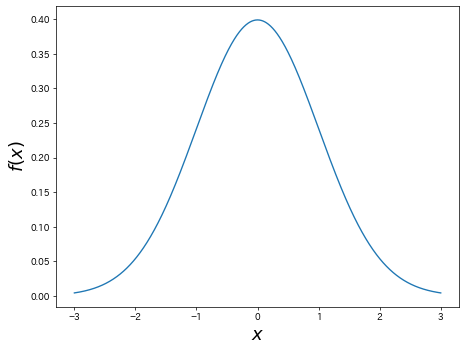
ガウス分布

平均 $\mu$，分散 $\sigma ^2$ のガウス分布の確率密度関数は，

$$\mathcal{N}\left(x | \mu, \sigma^2\right)=\frac{1}{\sqrt{2 \pi} \sigma} \exp \left(-\frac{(x-\mu)^2}{2 \sigma^2}\right)$$

で与えられます．平均 $0$，分散 $1$ のガウス分布 $\mathcal{N}(0, 1)$ は以下のようなつりがね型をした関数になっています．

多変量ガウス分布

1 変数のガウス分布を拡張した，多変量ガウス分布の確率密度関数は，

$$\mathcal{N}(\mathbf{x} | \boldsymbol{\mu}, \boldsymbol{\Sigma})=\frac{1}{(\sqrt{2 \pi})^D \sqrt{|\boldsymbol{\Sigma}|}} \exp \left(-\frac{1}{2}(\mathbf{x}-\boldsymbol{\mu})^T \boldsymbol{\Sigma}^{-1}(\mathbf{x}-\boldsymbol{\mu})\right)$$

で与えられます．ここで，$\mathbf{x} = (x_1, \dots , x_D)^T$ は $D$ 次元のベクトル，$\boldsymbol{\mu} = (\mu_1, \dots, \mu_D)^T$ は $\mathbf{x}$ の期待値を表す平均ベクトル，$\boldsymbol{\Sigma}$ は $D \times D$ の共分散行列です．共分散行列は $(i,j)$ 要素が $x_i$ と $x_j$ の共分散を表す行列で，$\boldsymbol{\Sigma} = E[\mathbf{x}\mathbf{x}^T] - E[\mathbf{x}]E[\mathbf{x}]^T$ です．

ガウス過程

入力の集合 $\mathbf{X} = (\mathbf{x_1},\dots, \mathbf{x_N})^T$ について，対応する出力 $\mathbf{f} = (f(\mathbf{x_1}), , \dots, f(\mathbf{x_N}))^T$ の同時確率分布 $p(\mathbf{f}|\mathbf{X})$ が平均 $\boldsymbol{\mu} = (\mu(\mathbf{x_1}), \dots , \mu(\mathbf{x_N}))^T$，共分散行列 $\mathbf{K}$ の多変量ガウス分布 $\mathcal{N}(\boldsymbol{\mu}, \mathbf{K})$ に従うとき，$f$ はガウス過程に従うといいます．この回帰モデルは，線形回帰モデルの重みについて期待値を取って積分消去することで導出されます．

ガウス過程は共分散行列 $\mathbf{K}$ によって特徴付けられ，その要素 $K_{nn'}$ は特徴ベクトルと呼ばれるベクトルの内積で計算されます．ですが，その特徴ベクトルを直接表現するのは大変なので，$K_{nn'}$ をカーネル関数 $k(\mathbf{x_n},\mathbf{x_{n'}})$ だけで計算するカーネルトリックを行います．カーネル関数から計算される共分散行列 $\mathbf{K}$ をカーネル行列またはグラム行列とも呼びます．

$$K_{nn'} = k(\mathbf{x_n},\mathbf{x_{n'}})$$

カーネル関数には様々な種類のものがありますが，ここでは RBF カーネル（ガウスカーネル）と呼ばれる次の式を使います．

$$k(\mathbf{x}, \mathbf{x}') = \theta_1 \exp \left(- \frac{|\mathbf{x} - \mathbf{x}'|^2}{\theta_2} \right)$$

$\theta_1, \theta_2 \in \R$ はハイパーパラメータで，勾配法のような最適化手法で最適化をします．RBF カーネルを用いると，無限回微分可能な滑らかな関数が出力されます．次の図は RBF カーネルを用いて適当にいくつかサンプリングしたものです．

ガウス過程回帰

ガウス過程回帰では，ガウス過程に基づいて予測分布を計算します．まず，$N$ 個の学習データ

$$\begin{aligned} \mathcal{D} &= \{ (\mathbf{x_1}, y_1), (\mathbf{x_2}, y_2), \dots, (\mathbf{x_N}, y_N) \}, \\ \mathbf{y} &= (y_1, \dots, y_N)^T \end{aligned}$$

が与えられているとします．ただし，式を簡単にするために平均を $\mathbf{0}$ とします．次に，予測したい入力を $\mathbf{X^*} = (\mathbf{x^*_1},\dots,\mathbf{x^*_M})^T$，予測したい出力を $\mathbf{y^*} = (y^*_1, \dots, y^*_M)^T$ とします．このとき，ガウス過程の予測分布は以下の式になります．

$$p\left(\mathbf{y^*} | \mathbf{X}^*, \mathcal{D}\right)=\mathcal{N}\left(\mathbf{k}_*^T \mathbf{K}^{-1} \mathbf{y}, \mathbf{k}_{* *}-\mathbf{k}_*^T \mathbf{K}^{-1} \mathbf{k}_*\right)$$

ここで，行列 $\mathbf{k}_*, \mathbf{k}_{* *}$ は次のように定義されます．

$$\begin{aligned} \mathbf{k}_*(n, m) & =k\left(\mathbf{x}_n, \mathbf{x}_m^*\right) \\ \mathbf{k}_{* *}(m, m) & =k\left(\mathbf{x}_m^*, \mathbf{x}_m^*\right) \end{aligned}$$

予測分布の式からわかるように，ガウス過程回帰では $N \times N$ の行列 $\mathbf{K}$ の逆行列 $\mathbf{K}^{-1}$ を計算する必要があります．その計算量は $O(N^3)$ で，学習データの数が膨大な場合には簡単に計算が出来ません．そこで，いくつかの近似手法が提案されています．詳しくは『ガウス過程と機械学習』の 5 章をご覧ください．

GPy を用いたガウス過程回帰

Python でガウス過程回帰を行えるライブラリはいくつかありますが，今回は GPy を用いてガウス過程回帰を試してみました．

インストール

GPy は pip でインストールができます．詳細は SheffieldML/GPy をご覧ください．

$ pip install GPy

ガウス過程回帰（入力・出力 1 次元）

今回は適当に作った関数からランダムにサンプリングをすることで学習データを作成し，それらを用いてガウス過程回帰を行います．ただし，グラフを簡単にするために入力・出力の次元は 1 次元とします．

各種ライブラリのインポート

import GPy
import numpy as np
import matplotlib.pyplot as plt

学習データの作成

正弦波を重ね合わせた関数を定義し，ガウス分布 $\mathcal{N}(0, 0.1^2)$ に従うノイズを加えています．

def func(x):
  return np.sin(2*np.pi*0.1*x) + np.sin(2*np.pi*0.2*x) + np.sin(2*np.pi*0.3*x)

n_train = 40
x_train = np.random.uniform(-10, 10, n_train)
y_train = func(x_train) + np.random.normal(0, 0.1, n_train)

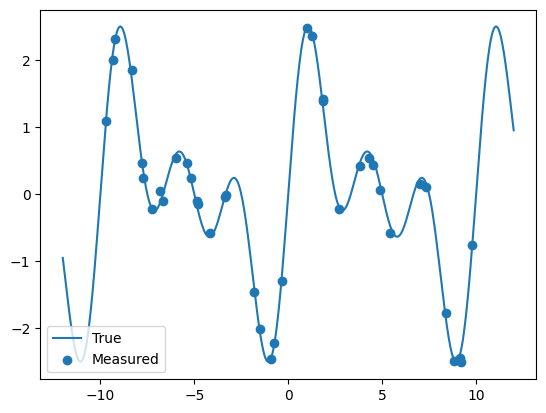
次の図は func(x) と $(\text{x\_train}, \text{y\_train})$ をプロットしたものです．

x_true = np.linspace(-12.0,12.0,500)
fig,axes = plt.subplots()
axes.plot(x_true, func(x_true), label="True")
axes.scatter(x_train,y_train, label="Measured")
axes.legend()
plt.show()

カーネルの定義とガウス過程回帰

今回は上述の RBF カーネルを使用します．必須の引数は入力の次元 input_dim です．ガウス過程回帰は GPy.models.GPRegression() で行えます．

kern = GPy.kern.RBF(1)
model = GPy.models.GPRegression(x_train.reshape(-1,1), y_train.reshape(-1,1), kern)
model

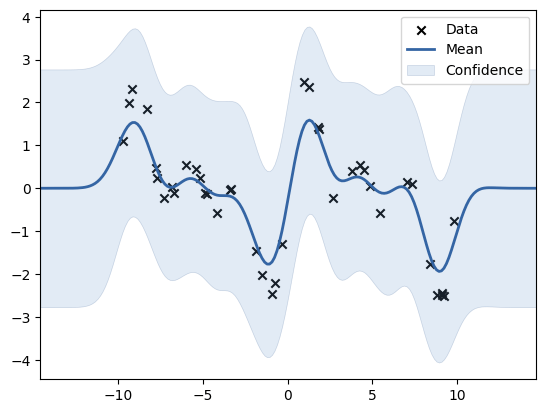
GPy には可視化用の関数が用意されているのでそれを使います．× は学習データ，青の実線は期待値，薄い青色の範囲は信頼区間を指します．

fig = plt.figure(figsize=(6,8))
fig,axes = plt.subplots()
model.plot(ax=axes)
plt.show()

現状では上手く回帰が出来ていないので，ハイパーパラメータを最適化します．GPy では関数 optimize() で最適化を行えます．

model.optimize(messages=True)

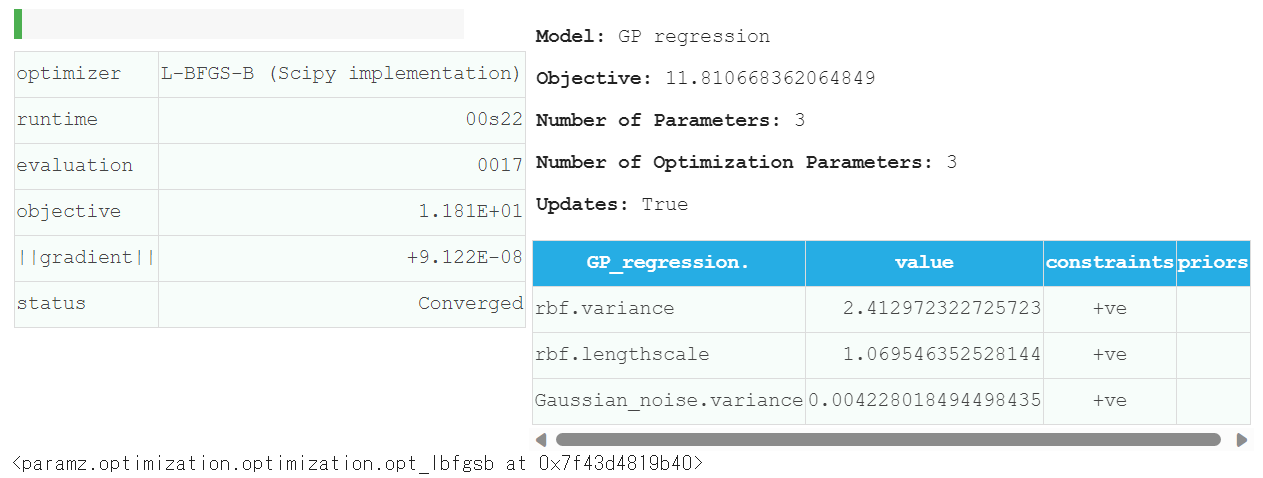
また，精度の悪い局所解を避けるために複数回の最適化を行う関数 optimize_restarts() も用意されています．引数 num_restarts で回数を指定します．今回は結果がほとんど変わらないことから，おそらく最適解が得られていると予想されます．

model.optimize_restarts(num_restarts = 10)

Optimization restart 1/10, f = 11.810668361597326
Optimization restart 2/10, f = 11.810668361508423
Optimization restart 3/10, f = 11.810668361673926
Optimization restart 4/10, f = 11.810668361659776
Optimization restart 5/10, f = 11.81066836149197
Optimization restart 6/10, f = 11.810668361486357
Optimization restart 7/10, f = 11.810668361489427
Optimization restart 8/10, f = 11.810668361494514
Optimization restart 9/10, f = 11.810668361664248
Optimization restart 10/10, f = 11.810668361552
[<paramz.optimization.optimization.opt_lbfgsb at 0x7f43d4819b40>,
 <paramz.optimization.optimization.opt_lbfgsb at 0x7f43d4819ae0>,
 <paramz.optimization.optimization.opt_lbfgsb at 0x7f43d7b57e20>,
 <paramz.optimization.optimization.opt_lbfgsb at 0x7f43d481b010>,
 <paramz.optimization.optimization.opt_lbfgsb at 0x7f43d4819bd0>,
 <paramz.optimization.optimization.opt_lbfgsb at 0x7f43d48b7580>,
 <paramz.optimization.optimization.opt_lbfgsb at 0x7f43d48b7880>,
 <paramz.optimization.optimization.opt_lbfgsb at 0x7f43d4818a60>,
 <paramz.optimization.optimization.opt_lbfgsb at 0x7f43d4819ba0>,
 <paramz.optimization.optimization.opt_lbfgsb at 0x7f43d481a740>,
 <paramz.optimization.optimization.opt_lbfgsb at 0x7f43d481bb50>]

次の図は最適化後の結果をプロットしたものです．最適化前と比べると明らかに回帰の精度が向上しています．データ数が少ない範囲では信頼区間が広くなっているので，その部分では自信がないということが明確にわかります．

fig = plt.figure(figsize=(6,8))
fig,axes = plt.subplots()
model.plot(ax=axes)
plt.show()

まとめ

本記事ではガウス過程回帰の概要について整理し，GPy を用いてガウス過程回帰を行いました．機械学習については初心者ですが，『ガウス過程と機械学習』は非常にわかりやすく楽しかったので，今更ですが記事を書いてみました．ガウス過程でここまで複雑なこともできるのかとワクワクしながら読み進めることができました．特にガウス過程とニューラルネットワークの関係性はびっくりしました．もう少し機械学習も勉強してみようという気分になりました．

参考

• 『ガウス過程と機械学習』
• GPy
• 公式 tutorial