## GNNを学ぶ_vol.4:データ可視化でグラフの「顔」を見る
こんにちは、古閑です。
前回のポスト:「## GNNを学ぶ_vol.3:時系列データの可視化で「季節性」を発見する」にて、個々のセンサー局の交通速度データをそのままプロットすると、ノイズが多く、全体的な傾向を掴むのが難しい場合があります。そこで、データセット全体を要約するために、**「平均」と「標準偏差」**を使ったグラフを可視化することでノイズに隠されていたデータ全体のパターンを発見することにとりくみました。今回のポストでは、各センサー局間の物理的な距離と、交通速度の相関関係をプロットすることにとりくみたいと思います。GNNのモデル学習に進みたい気持ちでいっぱいですが、今はぐっとこらえ、データの「顔」を見るための可視化作業を続けています。
今回は、交通予測に使うグラフデータが持つ**「物理的な繋がり」と「データの関係性」**を可視化しました。
前提:PeMSD7データセットについて
このデータセットの元データは、カリフォルニア州運輸局の**PeMS(Performance Measurement System)**から取得された、228箇所のセンサー局による交通速度データです。データは5分間隔に集約されています。
前回でおこなった可視化(時系列グラフで時間の変化を見る)
今回使用するデータセットは、5分間隔で交通速度を記録したものです。この交通速度が時間とともにどのように変化しているかを可視化するには、時系列グラフが最も適しています。
しかし、個々のセンサー局の交通速度データをそのままプロットすると、ノイズが多く、全体的な傾向を掴むのが難しい場合があります。
そこで、データセット全体を要約するために、**「平均」と「標準偏差」**を使ったグラフを可視化することにしました。この手法は、データ全体の変動の幅と中心的な傾向を同時に把握するのに非常に有効です。
コード:平均と標準偏差を可視化
# Plot mean/std traffic speed
mean = speeds.mean(axis=1)
std = speeds.std(axis=1)
plt.figure(figsize=(10,5), dpi=100)
plt.plot(mean, 'k-')
plt.grid(linestyle=':')
plt.fill_between(mean.index, mean-std, mean+std, color='r', alpha=0.1)
plt.xlabel('Time (5 min)')
plt.ylabel('Traffic speed')

1. 物理的な繋がりを見る:距離行列(Distance matrix)
GNNはノード間の関係性を学習するため、その**「物理的な距離」**を理解することが重要です。
以下のコードでは、distancesという変数に格納されたセンサー局間の距離データを可視化しました。
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8,8))
fig.tight_layout(pad=3.0)
ax1.matshow(distances)
ax1.set_xlabel("Sensor station")
ax1.set_ylabel("Sensor station")
ax1.title.set_text("Distance matrix")
この図は距離行列と呼ばれ、色が濃いほどセンサー局間の距離が近いことを示しています。このように、物理的な位置関係を可視化することで、GNNが学習するグラフ構造の全体像を把握できます。
2. データの関係性を見る:相関行列(Correlation matrix)
次に、各センサー局で観測された交通速度データ(speeds)の相関関係を可視化しました。
ax2.matshow(-np.corrcoef(speeds.T))
ax2.set_xlabel("Sensor station")
ax2.set_ylabel("Sensor station")
ax2.title.set_text("Correlation matrix")
plt.show()
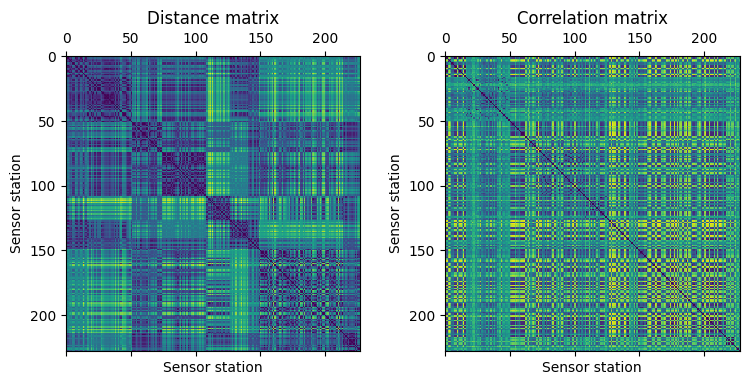
distancesという変数に格納されたセンサー局間の距離データと各センサー局で観測された交通速度データ(speeds)の相関関係を可視化した図
この図は相関行列と呼ばれ、色が濃いほどデータの関係性が強い(一方が上がるともう一方も上がる、または下がる)ことを示しています。この図から、物理的には離れていても、交通量や渋滞の傾向が似ているセンサー局同士の関係性を見つけることができます。
3. なぜ可視化が重要なのか?
GNNモデルは、この2つの行列から得られる情報(「物理的な繋がり」と「データの関係性」)を同時に学習します。
- 距離行列: グラフの「トポロジー(構造)」をモデルに伝えます。
- 相関行列: ノードが持つ「特徴量」の関係性をモデルに伝えます。
これらの可視化は、単なる作業ではなく、GNNが何を学習するのかを人間が直感的に理解するための、非常に重要な準備作業なのです。
今回の可視化を通して、データにどんなパターンが隠されているかが見えてきました。次回はいよいよ、このデータを使ってGNNモデルを構築し、交通予測に取り組んでみたいと思います。
備忘録:Hands on してみて手こずったところ
「Hands on GNN」を読みながら実行しているとうまく可視化できなかった部分があった。備忘録として手こずった部分とその原因を記録しておきたい。
- 枠しか表示されないんだけど…。
本書の指示どうりコードを入力していくも、枠しか表示されなかった…。
#1.We create affigure with two horizontal subplots and some padding between them:
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8,8))
fig.tight_layout(pad=3.0)
#2.First, we use the matshow() function to plot the distance matrix:
ax1.matshow(distances)
ax1.set_xlabel("Sensor station")
ax1.set_ylabel("Sensor station")
ax1.title.set_text("Distance matrix")
#3. them, so the two plots are easier to compare;
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(8,8))
fig.tight_layout(pad=3.0)
<AIによる解説>初学者向けのエラー対処法
今回、Hands on GNNのコードを実行した際、グラフが表示されず手こずりました。
原因は、plt.show()という、作成したグラフを画面に表示するための命令がコードに含まれていなかったためでした。matshow()などの描画関数だけでは、グラフは画面に現れません。
# グラフの作成
...
# 最後にこの一行を追加することで表示される
plt.show()
この経験から、コードの全体像を把握し、numpyのインポートやplt.show()といった基本命令が欠けていないかを確認することの重要性を再認識しました。
結論と今後の展望
今回の可視化を通して、データにどんなパターンが隠されているかが見えてきました。次回はいよいよ、このデータを使ってGNNモデルを構築し、交通予測に取り組んでみたいと思います。
参考文献
Hands-On Graph Neural Networks Using Python
Discussion