## GNNを学ぶ_vol.3:時系列データの可視化で「季節性」を発見する
前回のポスト:「## GNNを学ぶ Vol.1:グラフニューラルネットワーク入門」で、交通予測に使うPeMSD7データセットをダウンロードし、その時系列データを可視化しました。今回はその続きとして、データ全体の傾向をより深く探るための可視化手法を学びました。
時系列グラフでデータの変化を見る
前回の復習として、データセットと前回の可視化をおさらいします。
このデータセットは、5分間隔で交通速度を記録したものです。
* データセットについて:
引用文
"""
このデータセットは、PeMSD7データセットの中規模版です。
このデータセットの元データは、カリフォルニア州運輸局の**PeMS(Performance Measurement System)**というシステムから取得されました。このシステムは、カリフォルニア州の主要な高速道路に設置された約39,000台のセンサーから、リアルタイムの交通速度データを収集しています。
今回使用するデータセットでは、その中からカリフォルニア州第7区に位置する228箇所のセンサー局のデータのみを対象としています。データは2012年5月と6月の平日に収集されたものです。
元々は30秒ごとの速度計測データですが、このデータセットでは5分間隔に集約されています。
"""
まずは、この交通速度が時間とともにどのように変化しているかを可視化しました。
plt.figure(figsize=(10, 5))
plt.plot(speeds)
plt.grid(linestyle=':')
plt.xlabel('Time(5 min)')
plt.ylabel('Traffic speed')
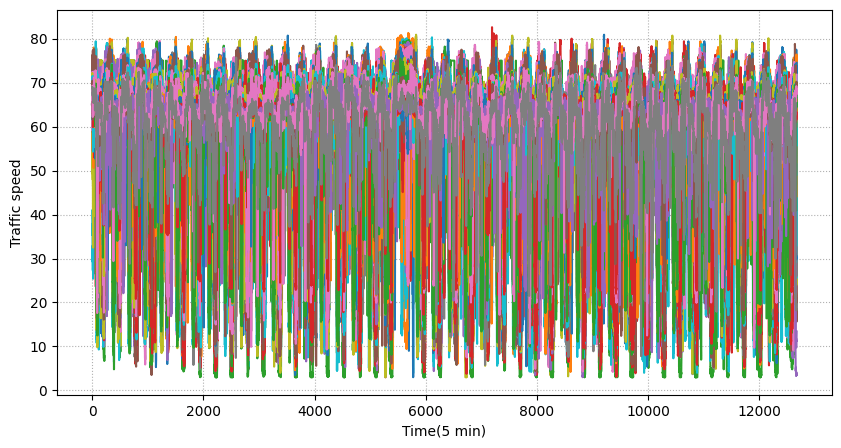
このグラフからは、個々のセンサー局のデータにノイズが多く、全体的な傾向を掴むのが難しいという課題が見えてきました。
ノイズに隠されたパターンを探る
個々のセンサー局の交通速度データをそのままプロットすると、ノイズが多く、全体的な傾向を掴むのが難しい場合があります。
そこで、データセット全体を要約するために、**「平均」と「標準偏差」**を使ったグラフを可視化することにしました。この手法は、データ全体の変動の幅と中心的な傾向を同時に把握するのに非常に有効です。
コード:平均と標準偏差を可視化
# Plot mean/std traffic speed
mean = speeds.mean(axis=1)
std = speeds.std(axis=1)
plt.figure(figsize=(10,5), dpi=100)
plt.plot(mean, 'k-')
plt.grid(linestyle=':')
plt.fill_between(mean.index, mean-std, mean+std, color='r', alpha=0.1)
plt.xlabel('Time (5 min)')
plt.ylabel('Traffic speed')
このコードでは、speedsデータから各タイムステップの平均(mean)と標準偏差(std)を計算し、matplotlibでプロットしています。plt.plot(mean, 'k-')で平均値を実線で描き、plt.fill_between()関数を使って、平均値の上下に標準偏差の範囲を塗りつぶしで表示しています。
可視化から見えたデータの特徴

生成されたグラフを見ると、ノイズに隠されていたデータ全体のパターンが鮮明に浮かび上がってきました。
- 明確な季節性(seasonality): 交通速度に、時間の経過とともに繰り返される明確なパターンがあることがわかります。朝の渋滞や夕方の帰宅ラッシュといった、日々の交通状況がパターンとして現れているようです。
- 高い変動性: グラフには、平均値から大きく外れた「スパイク」と呼ばれる急激な変動が多数見られます。これは、カリフォルニア州第7区全体にセンサーが配置されているため、一部のセンサーで交通が麻痺しても、他のセンサーでは正常な速度を記録しているといった、局所的な状況のばらつきを反映していると考えられます。
次なるステップ:相関関係の可視化
この可視化によって、データ全体の概要を把握できました。次に、各センサー局間の物理的な距離と、交通速度の相関関係をプロットすることで、より詳細な分析に進みたいと思います。物理的に近いセンサー同士は、似たような値を記録する傾向があるはずだからです。
追記10.12。AIによるコード解説
plt.fill_between(mean.index, mean-std, mean+std, color='r', alpha=0.1) がわからなかったので、AIに聞いて見た。
[AIによるコード解説:
plt.fill_between()は、「2つの線の間の領域を塗りつぶす」ための関数です。
この関数を使うことで、平均値の周りにデータのばらつき(この場合は標準偏差)の範囲を視覚的に表現することができます。これにより、単なる平均値の線だけでなく、データがどの程度の範囲で変動しているかを一目で把握できるようになります。
コードの引数解説
提示されたコードの 'plt.fill_between(mean.index, mean-std, mean+std, color='r', alpha=0.1)' の各部分を、一つずつ見ていきましょう。
mean.index: 塗りつぶしを行う**横軸(X軸)**の値を指定します。この例では、時系列データの時間のインデックス(タイムスタンプ)が使われています。
mean-std: 塗りつぶし範囲の下限(Y軸の下側の線)を指定します。この例では、「平均値(mean)から標準偏差(std)を引いた値」が使われています。
mean+std: 塗りつぶし範囲の上限(Y軸の上側の線)を指定します。この例では、「平均値(mean)に標準偏差(std)を足した値」が使われています。
color='r': 塗りつぶす色を指定します。'r'は**赤(red)**を意味します。
alpha=0.1: 塗りつぶしの透明度を指定します。0.0が完全に透明、1.0が不透明です。0.1という小さな値を設定することで、薄く塗りつぶし、グラフの他の部分が見えるようにしています。
この関数は、平均値を示すplt.plot(mean, 'k-')の線を中心に、データのばらつきの範囲を視覚的に強調するために使われています。]
Discussion