Zenn
📈

【Juliaで因果推論】相関関係と因果関係

2022/05/20に公開
Julia
#
因果推論
#
相関関係
#
因果関係
#
回帰分析
idea

相関関係と因果関係

例: サメ襲撃事件数とアイスクリームの売上高

サメ襲撃事件数とアイスクリームの売上高は非常に強い正の相関があるとされています．

  • サメ襲撃事件数が多いほどアイスクリームの売上高は大きくなる．
  • アイスクリームの売上高が大きいほどサメ襲撃事件数が多くなる．


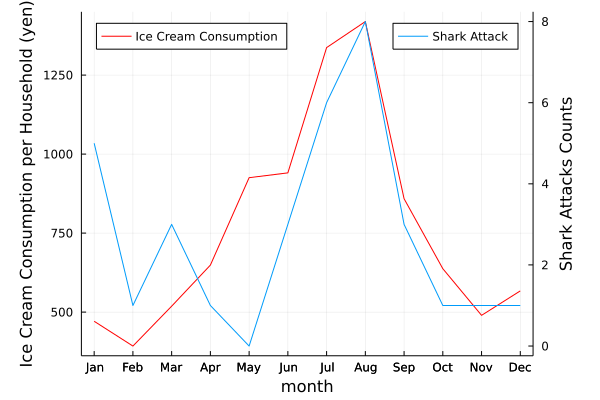
Figure.1 月別1世帯当たりアイスクリーム・シャーベット支出額[1]とサメ襲撃事件数[2]

Figure.1を見ると，サメ襲撃事件数とアイスクリームの売上高の増減はかなり似ていますね．海でサメに襲われる件数が多いほどとアイスクリームが良く売れる傾向があるので，

アイスクリーム屋さんは売上を増やすために海にサメを放流するべき

この提案は正しいのでしょうか?


Figure.2 サメ襲撃事件数が増えればアイスクリームの売上高は大きくなる?

この提案は，「サメはアイスの売上を増やす"原因"である」という考えに基づくものです．つまり，「サメ襲撃事件数の増加によってアイスクリームの売上高は増加するのか？」という問いに答えることができれば提案を評価することができます．

ここで，相関関係と因果関係の違いについて確認しておきます．

相関関係: X - Y

「Xが大きい（or 小さい）ほどYも大きい（or 小さい）」... 正の相関
「Xが大きい（or 小さい）ほどYは小さい（or 大きい）」... 負の相関

こういう傾向があるよってだけです．XとYの順番は関係なく，逆にしても全く同じ意味です．

因果関係: X \rightarrow Y

「他の条件を一定にしたとき，Xの変化によってYが変化する」

Xが原因であり，Yが結果です．ここで重要なのは他の条件を一定にしたとき[3]の部分です．仮に2つの平行世界があったとします．一方はサメ襲撃がある世界，もう片方はサメ襲撃がない世界で他の要素(気温，人の動き，経済状態, ...)は全て同じです．そしてこの2つの世界のアイスの売上を比較します．もし売上に違いが無ければ，サメとアイスに因果関係はないことになります．もし売上に違いがあれば，それは2つの平行世界のただ一つの違いであるサメ襲撃の有無に起因する他ないため，サメとアイスに因果関係はあると認めざるを得ません．

例: 学歴と賃金

教育年数が長い人ほど，将来の賃金は高くなる

このステートメントは正しそうでしょうか？賃金は学歴だけでは決まりません．例えば学力が高い人ほど賃金が高く、学力が高い人はそもそも高学歴な傾向があると考えられます．この"そもそも"という概念が非常に大切です．それでは，学力を一定にしたとき，教育年数が長い人ほど賃金は高くなるでしょうか？さらに他の条件（IQ，身長，体重，性別，年齢，見た目, 目に見えない能力...）も一定にしたとき，それでも教育年数が長い人ほど賃金は高くなるでしょうか？

例: 炭酸飲料と暴力

炭酸飲料を飲む子供ほど，暴力的になる

このステートメントは正しそうでしょうか？他の条件（性格，家庭環境，友人関係...）を一定にしても炭酸飲料を飲むか飲まないかの違いが暴力的になるかならないかの違いを生み出すでしょうか？

私たちが答えを求めている疑問の多くは因果関係・因果効果によって説明されます．

  • 教育年数Xを1年増やすことによって将来の賃金Yはどれくらい上がるのか？
  • 新薬処方をした場合(D=1)，新薬処方をしない場合(D=0)に比べて病状Yはどれくらい改善するのか？

ところが厄介なことに，相関関係があっても因果関係はないケースや，逆に相関関係がなくても因果関係はあるケースがあるため(Cunningham, 2021)，相関と因果の違いを理解して区別することが非常に重要になります．

ちなみにサメとアイスの間に強い正の相関関係が見られる理由は，どちらも共通して気温に依存しているからです[4]．気温が上がるとアイスクリームは良く売れるようになります．一方，気温が上がると海に出る人が増えて，かつサメの活動も活発になるため，サメに襲われる件数も増えます．結果として，「サメが増えたらアイスの売上も増える，サメが減ったらアイスの売上も減る」という相関関係[5]がでてきている状態です．


Figure.3 本当の因果関係 気温 \rightarrow アイス, 気温 \rightarrow サメ

しかし，サメとアイスの相関関係だけでは，サメとアイスの因果関係（サメの増減によってアイスの売上はどのくらい変化するのか）は見えてきません．相関関係だけに注目すると，サメとアイスには正の相関があるので，あたかもサメ襲撃事件数がアイスクリームの売上高を増やしているように見えてしまい，間違った解釈をしてしまう恐れがあります．

それでは，どのようにすれば「他の条件を一定にしたとき，Xの変化によってYは変化するのか？」という因果関係の問いに答えることができるでしょうか？次回はデータと仮定に基づく回帰分析を紹介して，因果関係に近づけるようにします．

Reference

Cunningham, S., 2021. Causal inference: the mixtape. Yale University Press.

脚注

  1. 2016年から2019年までの平均．出典: 総務省家計調査 https://www.stat.go.jp/data/kakei/longtime/index.html ↩︎

  2. 1945年から2018年までの総数．出典: Shark Research Institute, Inc. https://www.kaggle.com/datasets/felipeesc/shark-attack-dataset ↩︎

  3. ラテン語でceteris paribusと言います． ↩︎

  4. 疑似相関(spurious correlation)といいます． ↩︎

  5. 相関関係には順番がないので，「サメが増えたらアイスの売上も増える，サメが減ったらアイスの売上も減る」でも意味は全く同じです． ↩︎

Discussion