📉

【Juliaで因果推論】Difference-in-Differences: DID (差分の差分法)

2022/06/29に公開

Julia

$2 \times 2$ のパネルデータ:「処置群と対照群」「処置後と処置前」
「処置群の処置前後の差」と「対照群の処置前後の差」の差
差の差が因果効果であるためにはparalell trends assumptionが必要
DIDはtwo-way fixed effect regressionで推定

Difference-in-Differences: DID^[1] (差分の差分法)は，randomizedされていない処置の因果効果を推定する最も代表的な準実験(quasi-experimental)デザインの1つです．他のdesign-basedなリサーチデザイン(e.g., IV, RDD)はrandomizedされていない処置に対して何らかの方法で疑似的なrandomizationを作り出して因果効果を求める一方，non-design-basedなリサーチデザインであるDIDはrandomizationには頼らず，代わりにparallel trends assumption(平行トレンド仮定)を使います．DIDでは，処置を受ける処置群と処置を受けない対照群それぞれの，処置前時点と処置後時点のアウトカムの $2 \times 2$ のアウトカム(パネルデータ)を使います．DIDは因果効果を「"処置群と対照群の差分"と"処置後と処置前の差分"の差分」から求めるため，"差分の差分"と呼ばれます．DIDは(仮定はさておき)シンプルで分かりやすく，簡単に実行できるため，因果推論で一番人気な手法です．

$2 \times 2$ DID デザイン

DIDのクラシカルな例，Card and Krueger (1994) の「最低賃金の引上げが地域の雇用(従業員の人数)に与える影響」を考えます．

最低賃金の引上げという処置について，今回は処置群の平均処置効果 $ATT=\delta$ を知りたいとします．非現実的ですが，もし経済的・倫理的な制約が無くrandomized experimentが自由にできるのであれば，各地域に対してそれぞれ，最低賃金を引上げるか引上げないか $D = \{0, 1\}$ を地域の雇用 $Y$ ^[2](のpotential outcome $Y^1, Y^0$ )に関係なくコイン投げでランダムに決めちゃいましょう．するとindependence assumption ${Y^1,Y^0} \perp \!\!\! \perp D$ が成り立つ理想的な状況を無理矢理作り出すことができます．このとき引上げた地域とそうでない地域の平均雇用の差 $E[Y^1|D=1]-E[Y^0|D=0]$ そのものが最低賃金が雇用に与える因果効果となり，ATTをダイレクトに求めることができます．しかし，コイン投げで地域の最低賃金の引上げをアサインすることは現実的に無理なので，randomizationはできません．

一方，現実では1992年4月1日にニュージャージー州が最低賃金を＄4.25から＄5.05に引き上げています．また，隣接したペンシルバニア州^[3]では最低賃金が＄4.25のままでした．そこでCard and Krueger (1994)はこの2つの州を最低賃金の引き上げ前(1992年2月)と後(1992年11月)の2時点で比較することで，最低賃金の引上げが雇用に与える因果効果を分析します．

処置群と対照群の差分

まず初めに特に深く考えなければ「単純に州間のcross-sectionalな比較をすればいいのでは?」というアイディアが浮かびます．具体的には「手元に処置群と対照群のデータがあるから，引き上げ後1992年11月のニュージャージー州とペンシルバニア州の雇用の差を求めれば，それが最低賃金の引上げの効果だ」ということです．州 $s$ ，時点 $t$ の雇用を $Y_{st}$ とすれば，以下の差を求めることになります．

Y_{NJ,Nov} - Y_{PA,Nov}

ここで単純化^[4]のために，雇用 $Y_{st}$ はもともと時間を通じて変化しない要因(固定効果) $\gamma_{s}$ によって決定されているとします^[5]．最低賃金引上げが雇用に与える因果効果(ATT)を $\delta$ とすると，処置後1992年11月時点のニュージャージー州は処置を受けているので $Y_{NJ,Nov} = \gamma_{NJ} + \delta$ となり，ペンシルバニア州の雇用は処置を受けていないので固定効果だけの $Y_{PA,Nov} = \gamma_{PA}$ と表すことができます．この差をとると，

Y_{NJ,Nov} - Y_{PA,Nov} = \gamma_{NJ} + \delta - \gamma_{PA} = \delta + (\gamma_{NJ} - \gamma_{PA})

となるため，処置群と対照群の差は，推定したい因果効果 $\delta$ に $(\gamma_{NJ} - \gamma_{PA})$ を加えたものを計算していることになります． $(\gamma_{NJ} - \gamma_{PA})$ は処置を受けているニュージャージー州の処置前の効果と処置を受けていないペンシルバニア州の差なので，selection biasです．よって，単純な処置グループ間の処置後の差という推定方法では，不要なselection biasが混ざってしまい因果効果 $\delta$ を求めることができません．

States $s$	Time $t$	Outcome: $Y_{st}$	Difference
PA	Nov	$Y_{PA,Nov} = \gamma_{PA}$
NJ	Nov	$Y_{NJ,Nov} = \gamma_{NJ} + \delta$	$\delta + (\gamma_{NJ} - \gamma_{PA})$

処置後と処置前の差分

2つの州の固定効果の違いからselection biasが生じるため^[6]，州間の単純比較では因果効果は求まりません．そこで，今度はselection biasが嫌なので「同じ州内の処置後と処置前のtime seriesな比較をすればいいのでは？」と考えることができます．つまり「手元に処置後と処置前のデータがあるから，引き上げ後1992年11月のニュージャージー州と引き上げ前1992年2月のニュージャージー州の雇用の差を求めれば，それが最低賃金の引上げの効果だ」ということです．

Y_{NJ,Nov} - Y_{NJ,Feb}

異なる時点において，異なる雇用のトレンド(ここでは全ての州で共通のトレンドを想定します)があると考えるのは自然です．よって，時点固有のトレンド(時間固定効果) $\lambda_{t}$ を用いて各時点のアウトカムを表現すると，処置前1992年2月時点の処置群ニュージャージー州の雇用は $Y_{NJ,Feb} = \gamma_{NJ} + \lambda_{Feb}$ ，処置後1992年11月時点の処置群ニュージャージー州の雇用は $Y_{NJ,Nov} = \gamma_{NJ} + \lambda_{Nov} + \delta$ と表すことができます．差分をとると，

Y_{NJ,Nov} - Y_{NJ,Feb} = Y_{NJ,Nov} = (\gamma_{NJ} + \lambda_{Nov} + \delta) - (\gamma_{NJ} + \lambda_{Feb}) = \delta + (\lambda_{Nov} - \lambda_{Feb})

確かに，ニュージャージーの固定効果 $\gamma_{NJ}$ は差分をとることで相殺されます．しかし今度は新たに時間固定効果の差 $(\lambda_{Nov} - \lambda_{Feb})$ が残ってしまうので，処置後と処置前の単純比較をしても因果効果 $\delta$ を求めることができません．

States $s$	Time $t$	Outcome: $Y_{st}$	Difference
NJ	Feb	$Y_{NJ,Feb} = \gamma_{NJ} + \lambda_{Feb}$
NJ	Nov	$Y_{NJ,Nov} = \gamma_{NJ} + \lambda_{Nov} + \delta$	$\delta + (\lambda_{Nov} - \lambda_{Feb})$

差分の差分

処置群と対照群の差分も，処置後と処置前の差分もそれぞれ単体ではダメですが，この2つの差分の"差分"をとることで驚くほど簡単に因果効果を求めることができます．

States $s$	Time $t$	Outcome: $Y_{st}$	1st Diff $Y_{\cdot, Nov} - Y_{\cdot, Feb}$	2nd Diff $Y_{NJ, \cdot} - Y_{PA, \cdot}$
NJ	Nov	$Y_{NJ,Nov} = \gamma_{NJ} + \lambda_{Nov} + \delta$	$\delta + (\lambda_{Nov} - \lambda_{Feb})$	$\delta$
NJ	Feb	$Y_{NJ,Feb} = \gamma_{NJ} + \lambda_{Feb}$
PA	Nov	$Y_{PA,Nov} = \gamma_{PA} + \lambda_{Nov}$	$(\lambda_{Nov} - \lambda_{Feb})$
PA	Feb	$Y_{PA,Feb} = \gamma_{PA} + \lambda_{Feb}$

上の表を見ると，最初^[7]に処置後と処置前の差分をとっており，unit specificな固定効果 $\gamma_{NJ}, \gamma_{PA}$ が除去されます．次に，得られた処置後と処置前の差分に対して更に処置群と対照群の差分をとっており，時間固定効果の違いによるバイアス $(\lambda_{Nov} - \lambda_{Feb})$ が除去されます．このように差分の差分をとることで，「処置群と対照群の違い」と「処置後と処置前の違い」の両方をコントロールし，純粋な処置効果 $\delta$ を推定しようとするのがDIDのアイディアです．

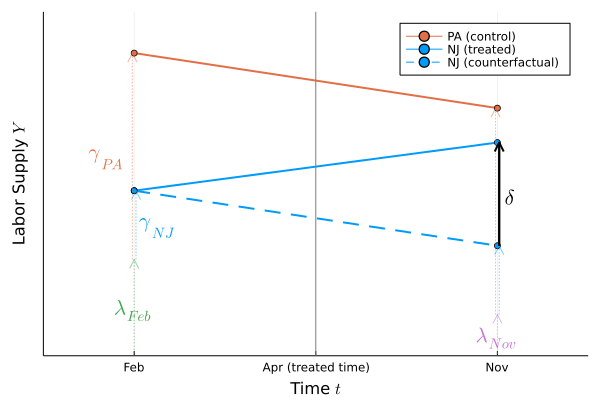
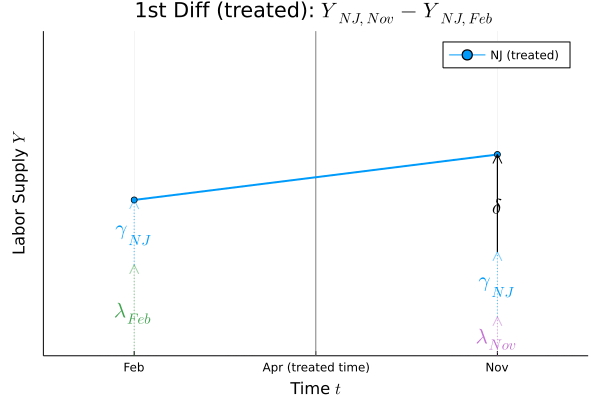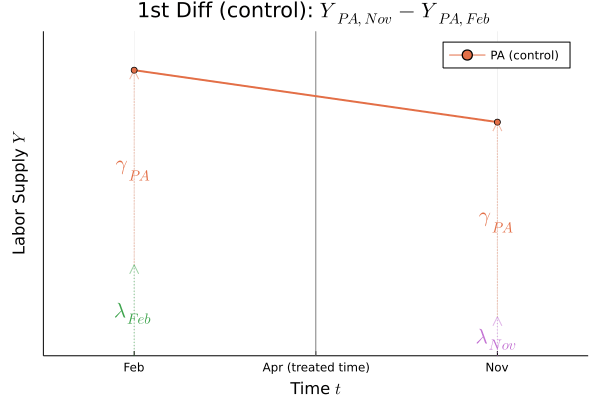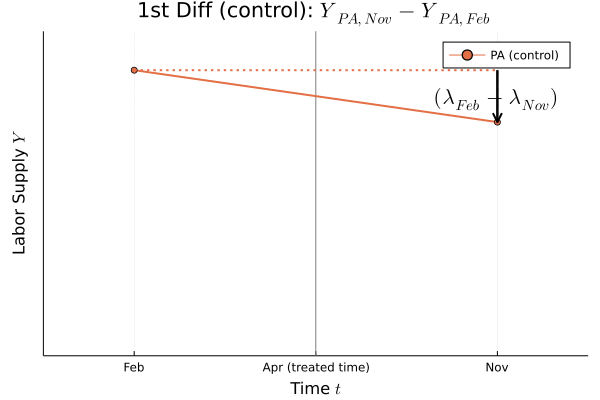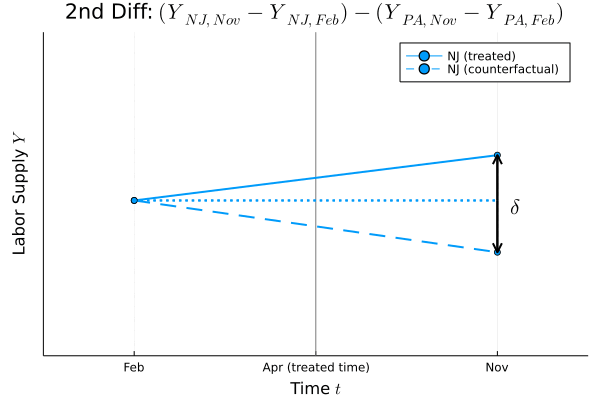
特に今扱っているような，処置のタイミング^[8]が処置群内で皆等しく，「処置群と対照群」の2グループと「処置後と処置前」の2時点のアウトカムを観測している典型的な状況のDIDを便宜上 $2 \times 2$ DIDデザイン^[9]と呼ぶことにします． $2 \times 2$ DIDに登場するパラメータ $\gamma_{NJ}, \gamma_{PA}, \lambda_{Nov}, \lambda_{Feb}, \delta$ を図示すると次のようになります．

Figure.1 $2 \times 2$ DIDのイメージ

Figure.1を見ると，どこが差の差なのかがはっきり分かります．この差の差の部分が処置効果 $\delta$ そのものであると言えるためには，後述するparallel trends assumption(平行トレンド仮定)が成り立っていることが必要となります．先に言ってしまうと，表やグラフを見てもわかる通り，DIDがうまくいくのは"時間を通じて変化する要素"が州の間で共通したトレンド(時間固定効果 $\lambda_t$ )だけであり州固有のトレンドがないと想定しているからです．つまり，処置群と対照群の時間を通じた変化は等しくなければいけないということです^[10]．仮に州固有のトレンドがあると，Figure.1のように処置群であるペンシルベニア州を下に引きずりおろしてニュージャージー州のcounterfactualとするのは不適切となります．

Parallel Trends Assumption (平行トレンド仮定)

先ほどは雑な表記の式と表・グラフをもとにざっくりとしたDIDについて議論しました．次に $2 \times 2$ DIDを少しきっちりと定式化して，DIDが良い推定となるためにはどんな条件が必要なのかを見てみます．

処置効果を推定するモデルを導入したり議論したりするために，Potential Outcomesフレームワークを使います．まずはPotential outcomes $Y^1_{ist}, Y^0_{ist}$ (ここでは実際のデータの単位を意識して店舗 $i$ レベルまで考えます)を書き出してみましょう^[11]．

\begin{align*} E[Y^1_{ist} | s, t] & = 時点t，州s，店舗iの，最低賃金引上げを受けた場合の期待雇用人数 \\ & = \gamma_s + \lambda_t + \delta \\ \\ E[Y^0_{ist} | s, t] & = 時点t，州s，店舗iの，最低賃金引上げを受けなかった場合の期待雇用人数 \\ & = \gamma_s + \lambda_t \end{align*}

今回求めたい母集団における処置効果はATT^[12]なので，処置を受けている $s=NJ, t=Nov$ の店舗における処置効果の期待値，

\begin{align*} ATT = \delta & = E[Y^1_{ist}-Y^0_{ist}|s=NJ, t=Nov] \\ & = E[Y^1_{ist}|s=NJ, t=Nov]-E[Y^0_{ist}|s=NJ, t=Nov] \end{align*}

を計算すればよいのですが，同じ $s, t$ の組合せのうち，観測されるのは片方のPotential outcomeのみです．観測できるのはfactualの $E[Y^1_{ist}|s=NJ, t=Nov]$ だけで，counterfactualである $E[Y^0_{ist}|s=NJ, t=Nov]$ ^[13]は観測できません．そこで次に，実際に観測されるアウトカムの仕組みをswitching equationで表してみましょう．処置を受けているかどうかは，パネルデータだと処置グループ $s$ と時点 $t$ の両方によって決まるので，処置ダミーを $D_{st}$ とします( $s=NJ$ かつ $t=Nov$ のとき $D_{st}=1$ ，それ以外は $D_{st}=0$ )．

\begin{align*} D_{st} & = \begin{cases} 1 & \text{if} \quad s=NJ \quad \text{and} \quad t=Nov \\ 0 & \text{otherwise} \end{cases} \end{align*}

swithing equationは次のようになります．

\begin{align*} Y_{ist} & = D_{st} Y^1_{ist} + (1 - D_{st}) Y^0_{ist} \end{align*}

（母集団の） $ATT=\delta$ を推定するため，DIDでは差分の差分 $\hat{\delta}^{2 \times 2}_{NJ, PA}$ を計算します．

\begin{align*} % \hat{\delta}^{2 \times 2}_{NJ, PA} = \left(E[Y_{ist}|s=NJ, t=Nov] - E[Y_{ist}|s=NJ, t=Feb]\right) - \left(E[Y_{ist}|s=PA, t=Nov] - E[Y_{ist}|s=PA, t=Feb]\right) \hat{\delta}^{2 \times 2}_{NJ, PA} = \underbrace{ \overbrace{\left(E[Y_{ist}|s=NJ, t=Nov] - E[Y_{ist}|s=NJ, t=Feb]\right)}^{\text{処置群}NJ\text{の処置後時点と処置前時点の差}} - \overbrace{\left(E[Y_{ist}|s=PA, t=Nov] - E[Y_{ist}|s=PA, t=Feb]\right)}^{\text{対照群}PA\text{の処置後時点と処置前時点の差}} }_{\text{処置群}NJの差と\text{対照群}PAの差の差} \end{align*}

ここで，switching equationを $\hat{\delta}^{2 \times 2}_{NJ, PA}$ に代入して，DIDの推定をpotential outcomesで表現してみると，

\begin{align*} \hat{\delta}^{2 \times 2}_{NJ, PA} = \left(E[Y^1_{ist}|s=NJ, t=Nov] - E[Y^0_{ist}|s=NJ, t=Feb]\right) - \left(E[Y^0_{ist}|s=PA, t=Nov] - E[Y^0_{ist}|s=PA, t=Feb]\right) \end{align*}

全ての項はfactualであり， $D_{st} = 1$ となるのは $s=NJ, t=Nov$ のときだけであることを意識しましょう．次に，テクニックとして $0 = E[Y^0_{ist}|s=NJ, t=Nov] - E[Y^0_{ist}|s=NJ, t=Nov]$ を加えて，DIDの推定 $\hat{\delta}^{2 \times 2}_{NJ, PA}$ の中から真の $ATT = \delta$ を見出します．

\begin{align*} \hat{\delta}^{2 \times 2}_{NJ, PA} & = \underbrace{ \left(E[Y^1_{ist}|s=NJ, t=Nov] - E[Y^0_{ist}|s=NJ, t=Feb]\right) - \left(E[Y^0_{ist}|s=PA, t=Nov] - E[Y^0_{ist}|s=PA, t=Feb]\right)}_{\text{swithing equation}} + \underbrace{E[Y^0_{ist}|s=NJ, t=Nov] - E[Y^0_{ist}|s=NJ, t=Nov]}_{0} \\ & = \underbrace{ \left(E[Y^1_{ist}|s=NJ, t=Nov] - E[Y^0_{ist}|s=NJ, t=Nov\right)}_{ATT = \delta} + \underbrace{\left(E[Y^0_{ist}|s=NJ, t=Nov]- E[Y^0_{ist}|s=NJ, t=Feb]\right) - \left(E[Y^0_{ist}|s=PA, t=Nov] - E[Y^0_{ist}|s=PA, t=Feb]\right)}_{\text{Non-parallel trends bias in } 2 \times 2 \text{ DID} } \\ \end{align*}

上の式から， $2 \times 2$ DIDが推定しているのは「真の処置効果 $ATT = \delta$ に邪魔なバイアス項がくっついたもの」であることが分かります．邪魔なバイアス項が0であれば， $2 \times 2$ DIDは真の処置効果ATTを綺麗にidentifyできるということになります．分析者としてはバイアス項が0であってほしいのですが，とりあえずバイアス項を詳しく見てみましょう．

\overbrace{( \underbrace{E[Y^0_{ist}|s=NJ, t=Nov]}_{\text{counterfactual}} - E[Y^0_{ist}|s=NJ, t=Feb] )}^{\text{処置群}NJ\text{が}\bf{処置を受けなかったとき}\text{の時間変化}} - \overbrace{\left(E[Y^0_{ist}|s=PA, t=Nov] - E[Y^0_{ist}|s=PA, t=Feb]\right)}^{\text{対照群}PA\text{の時間変化}}

このバイアスは「処置群が処置を受けなかったときの時間変化」が「対照群の時間変化」と等しいときに0となります．逆に，2つの処置グループ間で処置がないときの時間変化が異なっていればバイアスします．よって $2 \times 2$ DIDが真の処置効果を推定するためには，"処置がない仮想的な世界で処置群と対照群の時間変化(time trends)が平行(parallel)している" という仮定が必要となります．この仮定をparallel trends assumption (common trend assumption, 平行トレンド仮定)といいます．

Figure.2 Parallel trends assumption が成り立っていない場合の $2 \times 2$ DID

Figure.2では，parallel trends assumptionが成り立っていないときにDIDがなにを推定しているのかを図示しています．DIDのアイディアは，対照群 $PA$ の時間変化を，対照群 $NJ$ の処置を受けなかったときの時間変化として代用して処置効果を求めることです．しかしグラフを見ると，対照群 $PA$ の時間変化を $NJ$ のcounterfactualとして代用している点線は，本当の $NJ$ のcounterfactualの実線とは異なっているため，DIDの推定は間違っていることになります(この場合，DIDの推定は真のATTよりも過小評価することになります)．DIDが正しくATTを推定するためには「対照群 $PA$ の雇用人数の時間変化」が「(知る由もない)対照群 $NJ$ の処置を受けなかったときの雇用人数の時間変化」と"奇跡的に"一致しているというparallel trends assumptionが成り立っている必要があります．

Parallel trends assumptionはDIDが妥当な推定をするために一番重要な条件ですが，これが成り立っているかどうかを確認することはかなり困難です．なぜならバイアス項には観測されないcounterfactual $E[Y^0_{ist}|s=NJ, t=Nov]$ が含まれており，what ifな仮定であるため，モデルの推定から確認することはできません．よってDIDの妥当性は推定外で分析者がいかにオーディエンスを説得するかにかかっています．1つのアプローチとして考えられるのがplacebo test(e.g., DDD)です．placebo testについては別記事で紹介しようと思います．

Two-way fixed effect regression: TWFE (双方向固定効果モデル)

$2 \times 2$ DIDによる処置効果の推定は，そのまま標本平均の差の差を計算すればオッケーです．しかし，標準誤差の計算^[14]や他の変数をコントロールしたい場合^[15]，ただ差の差を計算するだけでは不十分です．そこで，実際のDIDの推定では回帰分析(regression-based DID)に落とし込んでやることが多いです^[16]．

DIDのswithing equationに戻りましょう．観測されるアウトカムのうち，potential outcomes以外の決定要因を誤差項 $\epsilon_{ist}$ (ただし $E[\epsilon_{ist}|s,t]=0$ )として考慮すると^[17]，swithing equationから線形回帰モデルを導くことができます．

\begin{align*} Y_{ist} & = D_{st} Y^1_{ist} + (1 - D_{st}) Y^0_{ist} + \epsilon_{ist} \\ & = D_{st} (\gamma_s + \lambda_t + \delta) + (1 - D_{st}) (\gamma_s + \lambda_t) + \epsilon_{ist} \\ & = \gamma_s + \lambda_t + \delta D_{st} + \epsilon_{ist}, \quad E[\epsilon_{ist}|s,t]=0 \\ \end{align*}

$\gamma_s$ が処置グループの固定効果， $\lambda_t$ が時間固定効果なので，DIDの正体は Two-way fixed effect regression: TWFE (双方向固定効果モデル) です．TWFEは差の差と同様，「処置グループ間の違い」と「時点間の違い」の両方を固定効果としてコントロールします．よってこの回帰モデルTWFEを推定して得られる処置ダミーの係数の推定値 $\hat{\delta}^{2 \times 2 \text{TWFE}}_{NJ, Nov}$ は，ダイレクトに差の差から計算される処置効果の推定値 $\hat{\delta}^{2 \times 2}_{NJ, Nov}$ と全く同じものとなります．TWFEの推定は，通常の固定効果モデルのwhithin推定をすればいいです．処置グループの固定効果に加え，時点固定効果，処置ダミーをモデルに含めましょう．

ちなみに，TWFEはwithin推定する代わりに，固定効果を全てダミー変数に置き換えて単純なOLS推定をしても同じ結果が得られます．処置グループの固定効果の代わりに $NJ_{s}$ (ニュージャージー州なら1)，時間固定効果の代わりに $d_{t}$ (1992年11月なら1)の2つのダミー変数を考えます．また，処置ダミー $D_{st}$ は2つのダミー変数の交差項 $D_{st} = NJ_{s} \cdot d_{t}$ として表すことができるので，DIDのTWFEの式は次の線形回帰モデルに書き換えることができます．

\begin{align*} Y_{ist} = \alpha + \gamma NJ_{s} + \lambda d_{t} + \delta (NJ_{s} \cdot d_{t}) + \epsilon_{its} \end{align*}

求めたい処置効果は，11月かつニュージャージー州のときのみ1となる交差項 $NJ_{s} \cdot d_{t}$ の係数の推定値 $\hat{\delta}^{2 \times 2 \text{OLS}}_{NJ, Nov}$ ^[18]となります．2つの固定効果と処置ダミーをwithin推定するにしろ，固定効果をダミー変数にしてOLS推定するにしろ，結局 $2 \times 2$ DIDはプラクティカルにはTWFEで推定されることが多いです．

ちなみに標準誤差については，処置グループ内の誤差項の相関を考慮するため，少なくとも処置グループレベルでClustered-Robust標準誤差を計算しましょう．

ここでもう一度注意しておきたいこととしてparallel trends assumptionが成り立つかどうかはモデル推定では確認できません．本当のcounterfactual が何なのかはモデルであるTWFEにとって知ったことではありません．TWFEがやることは，ただただ対照群と同じ時間を通じた変化を，処置群に平行して機械的に当てはめているだけです．counterfactualが観測されない以上，数値的にチェックすることはできないのでparalell trends assumptionが成り立っているかどうかは推定外の分析者のrobustness checkにゆだねられます．

例: 最低賃金と雇用 Card and Krueger (1994)

それではCard and Krueger (1994)の最低賃金と雇用の実際のデータを用いてDIDをやってみましょう．

# data wrangling
using CSV, DataFrames, GLM, StatsBase, Statistics

name = [
    :SHEET,:CHAIN,:CO_OWNED,:STATE,:SOUTHJ,:CENTRALJ,:NORTHJ,:PA1,:PA2,:SHORE,:NCALLS,:EMPFT,:EMPPT,:NMGRS,:WAGE_ST,:INCTIME,:FIRSTINC,:BONUS,:PCTAFF,:MEALS,:OPEN,:HRSOPEN,:PSODA,:PFRY,:PENTREE,:NREGS,:NREGS11,:TYPE2,:STATUS2,:DATE2,:NCALLS2,:EMPFT2,:EMPPT2,:NMGRS2,:WAGE_ST2,:INCTIME2,:FIRSTIN2,:SPECIAL2,:MEALS2,:OPEN2R,:HRSOPEN2,:PSODA2,:PFRY2,:PENTREE2,:NREGS2,:NREGS112
]

njmin = DataFrame(CSV.File("public.dat", header=false, delim=' ', ignorerepeated=true, missingstrings="."))
rename!(njmin, name)

# STATE: 1 if NJ; 0 if Pa
# EMPFT: full-time employees (Feb)
# EMPPT: part-time employees (Feb)
# NMGRS: managers/ass't managers (Feb)
# WAGE_ST: starting wage ($/hr) (Feb)
# EMPFT2: full-time employees (Nov)
# EMPPT2: part-time employees (Nov)
# NMGRS2: managers/ass't managers (Nov)
# WAGE_ST2: starting wage ($/hr) (Nov)

njmin = njmin[:, [:STATE, :EMPFT, :EMPPT, :NMGRS, :WAGE_ST, :EMPFT2, :EMPPT2, :NMGRS2, :WAGE_ST2]]
dropmissing!(njmin) # omit missing for simplisity

njmin.EMPFEB = njmin.EMPFT + njmin.NMGRS + .5 * njmin.EMPPT # full-time-equivalent employment in Feb
njmin.EMPNOV = njmin.EMPFT2 + njmin.NMGRS2 + .5 * njmin.EMPPT2 # full-time-equivalent employment in Nov

describe(njmin)

まずはデータの分布を見てみましょう．1992年2月と1992年11月の，それぞれの州の賃金の分布は次の通りです．

using Plots, StatsPlots

colors = theme_palette(:auto)

l = @layout [grid(1, 2)]
p1 = @df njmin groupedhist(:WAGE_ST, group=:STATE, bar_position=:dodge, bins=14, labels=["PA" "NJ"], color=[colors[2] colors[1]])
title!("Feb 1992")
p2 = @df njmin groupedhist(:WAGE_ST2, group=:STATE, bar_position=:dodge, bins=14, labels=["PA" "NJ"], color=[colors[2] colors[1]])
title!("Nov 1992")
plot(p1, p2, layout = l)
xlabel!("Wage")
ylabel!("# stores")

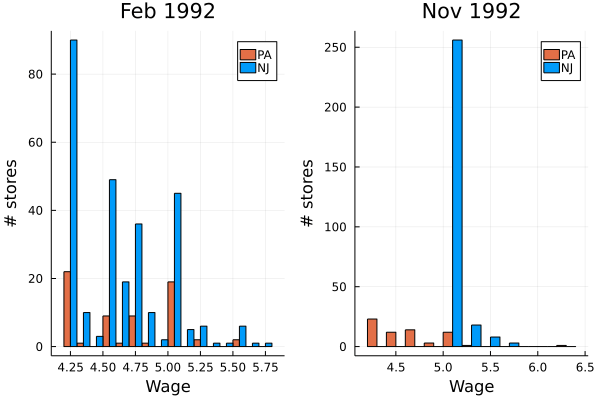
ニュージャージー州だけが1992年4月に最低賃金が＄4.25から＄5.05に引き上げられたため，11月のニュージャージー州の時給の分布では＄5.05が最小となっています．

単純な差の差によるDID

次に単純な差の差を直接計算してみましょう．

# stack to panel data
njmin.ID = rownumber.(eachrow(njmin))

panel = stack(njmin, [:EMPFEB, :EMPNOV], [:ID, :STATE])
rename!(panel, [:ID, :NJ, :d, :FTE])
panel.d = ifelse.(panel.d .== "EMPNOV", 1, 0)

panel
# 702 rows × 4 columns

# ID	NJ	d	FTE
# Int64	Int64	Int64	Float64
# 1	1	0	0	34.0
# 2	2	0	0	24.0
# 3	3	0	0	70.5
# 4	4	0	0	23.5
# 5	5	0	0	11.0

# simple diff in diff

# average in 2 by 2
mean_FTE_NJ_NOV = mean(panel[(panel.NJ .== 1) .& (panel.d .== 1), :FTE])
mean_FTE_NJ_FEB = mean(panel[(panel.NJ .== 1) .& (panel.d .== 0), :FTE])
mean_FTE_PA_NOV = mean(panel[(panel.NJ .== 0) .& (panel.d .== 1), :FTE])
mean_FTE_PA_FEB = mean(panel[(panel.NJ .== 0) .& (panel.d .== 0), :FTE])

print("average full-time employment (NJ, Nov): ", mean_FTE_NJ_NOV, "\n")
print("average full-time employment (NJ, Feb): ", mean_FTE_NJ_FEB, "\n")
print("average full-time employment (PA, Nov): ", mean_FTE_PA_NOV, "\n")
print("average full-time employment (PA, Feb): ", mean_FTE_PA_FEB, "\n")

# 1st diff
print("1st diff in NJ (time-series diff): ", mean_FTE_NJ_NOV - mean_FTE_NJ_FEB, "\n")
print("1st diff in PA (time-series diff): ", mean_FTE_PA_NOV - mean_FTE_PA_FEB, "\n")

print("1st diff in NOV (cross-sectional diff): ", mean_FTE_NJ_NOV - mean_FTE_PA_NOV, "\n")
print("1st diff in FEB (cross-sectional diff): ", mean_FTE_NJ_FEB - mean_FTE_PA_FEB, "\n")

# 2nd diff
print("2nd diff: ", (mean_FTE_NJ_NOV - mean_FTE_NJ_FEB) - (mean_FTE_PA_NOV - mean_FTE_PA_FEB), "\n")

#average full-time employment (NJ, Nov): 21.076315789473686
#average full-time employment (NJ, Feb): 20.678245614035088
#average full-time employment (PA, Nov): 21.825757575757574
#average full-time employment (PA, Feb): 23.704545454545453
#1st diff in NJ (time-series diff): 0.3980701754385976
#1st diff in PA (time-series diff): -1.878787878787879
#1st diff in NOV (cross-sectional diff): -0.7494417862838887
#1st diff in FEB (cross-sectional diff): -3.026299840510365
#2nd diff: 2.2768580542264765

mean $FTE$	$NJ$	$PA$	$NJ-PA$
$Nov$	21.08	21.83	-0.75
$Feb$	20.68	23.70	-3.03
$Nov-Feb$	0.40	-1.88	2.28

プロットすると次のようになります．

using Plots, LaTeXStrings

Feb = -1
Apr = 0
Nov = 1

Y_NJ_Nov = 21.08
Y_NJ_Feb = 20.68
Y_PA_Nov = 21.83
Y_PA_Feb = 23.70
Y_NJ_Nov_counter = Y_NJ_Nov - ((Y_NJ_Nov - Y_NJ_Feb) - (Y_PA_Nov - Y_PA_Feb))

colors = theme_palette(:auto)

plot([Feb, Nov], [Y_PA_Feb, Y_PA_Nov], marker=true, color=colors[2], label="PA (control)", width=2)
plot!([Feb, Nov], [Y_NJ_Feb, Y_NJ_Nov], marker=true, color=colors[1], label="NJ (treated)", width=2)
plot!([Feb, Nov], [Y_NJ_Feb, Y_NJ_Nov_counter], marker=true, color=colors[1], linestyle=:dash, label="NJ (counterfactual)", width=2)
vline!([Apr], label=false, color=:gray)

plot!([Nov, Nov], [Y_NJ_Nov_counter, Y_NJ_Nov], line=:arrow, label=false, color=:black, width=2)
annotate!(Nov-0.1, Y_NJ_Nov_counter+(Y_NJ_Nov-Y_NJ_Nov_counter)/2, Plots.text(L"\hat{\delta}^{2 \times 2}", :black))

xlabel!("Time")
ylabel!("mean FTE")
xticks!([Feb, Apr, Nov], ["Feb", "Apr (treated time)", "Nov"])

処置なしのニュージャージー州とペンシルバニア州のフルタイム従業員数の時間変化にparallel trends assumptionが成り立っているのであれば，処置効果ATTは2.28です．つまり，処置群ニュージャージー州において「最低賃金引き上げによって1店舗当たり平均でフルタイム従業員数が2.28人増加する」ということになります．

最後に同じDIDを回帰モデルTWFEで推定してみましょう．

TWFEによるDID (ダミー変数でOLS推定)

TWFEの州固定効果と時間固定効果をダミー変数^[19]とし，2つのダミー変数の交差項をモデルに入れてOLS推定する方法をやってみましょう．

using GLM, CovarianceMatrices

twfe_ols = lm(@formula(FTE ~ NJ + d + NJ&d), panel)

# StatsModels.TableRegressionModel{LinearModel{GLM.LmResp{Vector{Float64}}, GLM.DensePredChol{Float64, LinearAlgebra.CholeskyPivoted{Float64, Matrix{Float64}}}}, Matrix{Float64}}

# FTE ~ 1 + NJ + d + NJ & d

# Coefficients:
# ────────────────────────────────────────────────────────────────────────
#                 Coef.  Std. Error      t  Pr(>|t|)  Lower 95%  Upper 95%
# ────────────────────────────────────────────────────────────────────────
# (Intercept)  23.7045      1.14845  20.64    <1e-73   21.4497   25.9594
# NJ           -3.0263      1.27451  -2.37    0.0178   -5.52864  -0.523961
# d            -1.87879     1.62416  -1.16    0.2478   -5.06761   1.31003
# NJ & d        2.27686     1.80243   1.26    0.2069   -1.26198   5.8157
# ────────────────────────────────────────────────────────────────────────

交差項 $NJ_s \cdot d_t$ の係数を見てみると，点推定値は差の差と同じ値 $\hat{\delta}^{2 \times 2}=2.28$ が得られます．

一応下ではクラスター標準誤差を計算していますが，クラスターが少ない(今回は2つ，処置群は1つだけ)ときクラスター標準誤差はfalse positive(偽陽性，第一種過誤)を招く傾向があるので，標準誤差に関しては適切な計算ができていないかもしれません．

stderror(CRHC1(:NJ, panel), twfe_ols)

# 4-element Vector{Float64}:
#  6.316738594668046e-14
#  6.348676678374231e-14
#  8.460462682955149e-14
#  8.467259838575548e-14

TWFEによるDID (within推定)

TWFEを固定効果モデルのwhithin推定でやってみましょう．

using FixedEffectModels

# treatment dummy
panel.D = panel.NJ .& panel.d
CSV.write("njmin_panel.csv", panel)

reg(panel, @formula(FTE ~ fe(NJ) + fe(d) + D), Vcov.cluster(:NJ))

#                      Fixed Effect Model                     
# =============================================================
# Number of obs:            702   Degrees of freedom:         4
# R2:                     0.009   R2 Adjusted:            0.004
# F-Stat:                   NaN   p-value:                  NaN
# R2 within:              0.002   Iterations:                 2
# =============================================================
# FTE | Estimate Std.Error t value Pr(>|t|) Lower 95% Upper 95%
# -------------------------------------------------------------
# D   |  2.27686       0.0     Inf    0.000   2.27686   2.27686
# =============================================================

このように回帰分析のパッケージを使って，DIDをTWFEとして簡単に推定することができます．

Refference

Cunningham, S., 2021. Causal inference: the mixtape. Yale University Press.
Angrist, J.D. and Pischke, J.S., 2008. Mostly harmless econometrics. In Mostly Harmless Econometrics. Princeton university press.
Huntington-Klein, N., 2021. The effect: An introduction to research design and causality. Chapman and Hall/CRC.
Card, David, and Alan Krueger. 1994. “Minimum Wages and Employment: A Case Study of the Fast-Food Industry in New Jersey and Pennsylvania.” American Economic Review 84: 772–93.
Goodman-Bacon, A., 2021. Difference-in-differences with variation in treatment timing. Journal of Econometrics, 225(2), pp.254-277.

脚注

DDなどと表記することもあります． ↩︎
Card and Krueger (1994)では $ファストフード店のフルタイムの従業員 + 0.5 パートタイムの従業員$ としています． ↩︎
ペンシルバニア州はニュージャージー州と隣接しており，多くの性質が似ていて比較可能と考えられるので，実質上で他の条件 $X$ をコントロールしていることになります(spill overの可能性もありますが)． ↩︎
time invariantな固定効果だけでも処置群と対照群の差は因果効果の推定としては適切ではないとわかるので，time variantな要素が州の間で異なるといった議論はここでは不要と考えていいです． ↩︎
固定効果は観測されず，時間を通じて変化しない州固有の全ての要素です ↩︎
処置が州間でrandomizedされていないってことです． ↩︎
cross-sectionalな差分とtime-seriesな差分の順番は関係ありません． ↩︎
異なるタイミングの処置効果に $2 \times 2$ DIDを使うとかなりややこしいことになります(Goodman-Bacon, 2019)． ↩︎
Goodman-Bacon (2019)でこのように呼ばれています． ↩︎
2つのグループのトレンドが同じだと決めつけるのは一般的に不自然なので，parallel trends assumptionは結構強い仮定です． ↩︎
母集団のCEFを意識して，期待値表記をしています(Angrist and Pischke, 2008 p.170)． ↩︎
ATTは一定であると考えています． ↩︎
1992年4月にニュージャージー州全域で最低賃が引上げられているので，その後1992年11月のニュージャージー州の中で最低賃金引上げを受けていない店舗は存在しません． ↩︎
これについては普通に平均の差の検定をすればいいです． ↩︎
ある変数を条件付けするとParalell trends assumptionが成り立ちそうなとき，コントロールを入れるインセンティブが生まれます．固定効果モデルなので，入れられるコントロール変数はグループ間にも時点間にもvariationがあるものだけです． ↩︎
回帰分析に落とし込めれば，推定の議論がなじみのある回帰分析ベースでできたり，そこら中にある回帰分析のパッケージを使ってすぐ簡単に分析ができるので都合がいいです． ↩︎
正直どのタイミングでDIDの誤差項を入れるべきかよくわかんないです．最初からswitching equationに入れるべきかもしれません ↩︎
以後推定の表記については，差の差，TWFE，OLSは同値なので，区別せず $\hat{\delta}^{2 \times 2}$ とします． ↩︎
今回の例では，2グループ，2時点だけなので，特に新しくダミーを立てる必要はありません． ↩︎