楕円曲線暗号のPythonによる実装その2（楕円曲線とECDSA）

お断り

この記事は『Software Design2022年3月号』の「第4章：電子署名のプロセスを体験 Pythonによる楕円曲線暗号の実装」の入稿記事を技術評論社のご好意で公開したものです。
元はLaTeXだったのをマークダウンに修正し、二つに分けています。
前半は楕円曲線暗号のPythonによる実装その1（有限体とECDH鍵共有）です。
記事中のサンプルコードはサポートページからダウンロードできます。

楕円曲線クラス

楕円曲線の点

有限体クラスを実装できたので次は楕円曲線クラス$\texttt{Ec}$を実装します。
楕円曲線は有限体$\texttt{Fp}$とその値$a$と$b$で決まります。
楕円曲線クラスは楕円曲線の節で紹介したように$r$個の点0, $P$, $2P$, ....からなる集合です。

secp256k1はTLSやビットコインで使われる楕円曲線のパラメータで、

$$a=0$$

$$b=7$$

$$p=2^{256} - 2^{32} - 2^9 - 2^8 - 2^7 - 2^6 - 2^4 - 1$$

$$r=\text{0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141}$$

となっています（SEC 2: Recommended Elliptic Curve Domain Parameters）。

それらの値をクラスメソッド$\texttt{init}$で設定します。

class Ec:
    @classmethod
    def init(cls, a, b, r):
        cls.a = a
        cls.b = b
        cls.r = r

Ec::init

楕円曲線の点は2個の$\texttt{Fp}$の要素で表現できます。$P=(x,y)$。ただし、$O$は整数の0に相当する特別な点（以降0と表示する）で場合分けが必要です。
そのためメンバ変数として$x$, $y$の他に0か否かを表すフラグisZeroを用意します。
$(x, y)$は方程式$y^2=x^3+ax+b$を満たさなければなりません。

値が正しいか否かを確認する$\texttt{isValid}$メソッドを用意しましょう。isZeroがTrueのときはTrueです。

def isValid(self):
    if self.isZero:
        return True
    a = self.a
    b = self.b
    x = self.x
    y = self.y
    return y*y == (x*x+a)*x+b

Ec::isValid

楕円曲線の点の足し算

楕円曲線の点の足し算、引き算の規則を紹介します。
まず点0と任意の点$P$に対して$P+0=0+P=P$とします。
また$P=(x_1,y_1)$のとき、$-P=(x_1,-y_1)$と定義します。点のマイナスは$y$座標の値の符号を反転します。
$P$と$-P$を足すと常に0です。$P+(-P)=0$。
そして一般の点$P=(x_1,y_1)$と$Q=(x_2,y_2)$について$R=(x_3,y_3)=P+Q$は次の計算をします。

加法公式

式は複雑ですが、四則計算だけなので有限体の節で実装した有限体を使って計算できます。
なぜこんな式が現れるのかについてはたとえば拙著『クラウドを支えるこれからの暗号技術』などを参照ください。
この式をそのままPythonで実装します。

def __add__(self, rhs):
    if self.isZero:
        return rhs
    if rhs.isZero:
        return self
    x1 = self.x
    y1 = self.y
    x2 = rhs.x
    y2 = rhs.y
    if x1 == x2:
        # P + (-P) = 0
        if y1 == -y2:
            return Ec()
        # dbl
        L = x1 * x1
        L = (L + L + L + self.a) / (y1 + y1)
    else:
        L = (y1 - y2) / (x1 - x2)
    x3 = L * L - (x1 + x2)
    y3 = L * (x1 - x3) - y1
    return Ec(x3, y3, False)

Ec::add

楕円曲線の点の整数倍

最後に楕円曲線の点の整数倍を実装します。
$n$倍の$P$を$2P = P + P$, $3P = 2P + P$, $4P = 3P + P$と逐次的に求めようとすると、$n$が256ビット整数のときは宇宙が滅亡しても全く終わりません。
そこで効率のよい方法を紹介します。

$n=11=0b1011$（2進数表記）とすると、$0b1011=0b1010 + 1 = (2 \times 0b101) + 1$となるので、

$$Q=0b1011 P =(2 \times 0b101 + 1)P = 2(0b101 P) + P$$

と表せます。次に$0b101 P$に対して同様のことを再帰的に繰り返すと

$$Q=2(0b101 P) + P =2(2 (0b10 P) + P) + P = 2(2 (2 P) + P) + P$$

つまり$n$を2進数で表したとき、点$P$の上位$k$ビット倍が求まったら、
その値を2倍して次のビットが1なら$P$を足すことで$k+1$ビット倍が求まり、それを繰り返すのです。
この方法では、ループ回数は$n$のビット長になるので256ビット整数でも高々256回のループで完了します。

Pythonで実装するには、まず$n$を$\texttt{bin(n)}$で2進数表記し、$\texttt{0b...}$で始まる最初2文字を取り除いた0と1からなる文字列に対してループさせます。

def __mul__(self, rhs):
    if rhs == 0:
        return Ec()
    bs = bin(rhs)[2:]
    ret = Ec()
    for b in bs:
        ret += ret
        if b == '1':
            ret += self
    return ret

Ec::mul

以上でECDH鍵共有に必要なメソッドの実装が完了しました。

ECDSAの実装

最後に楕円曲線を用いた署名の一つであるECDSAを実装しましょう。

署名の概要

署名は鍵生成、署名（sign）、検証（verify）の3個のアルゴリズムからなります。
鍵生成ではアリスが署名鍵sと検証鍵Sを生成します。署名鍵sは自分だけの秘密の値なので秘密鍵、検証鍵Sは他人に渡して使ってもらう鍵なので公開鍵ともいいます。
signは署名したいデータmに対して署名鍵sで署名と呼ばれるデータσを作ります。
secp256k1曲線の場合は2個の256ビット整数からなる512ビットの固定長データです。

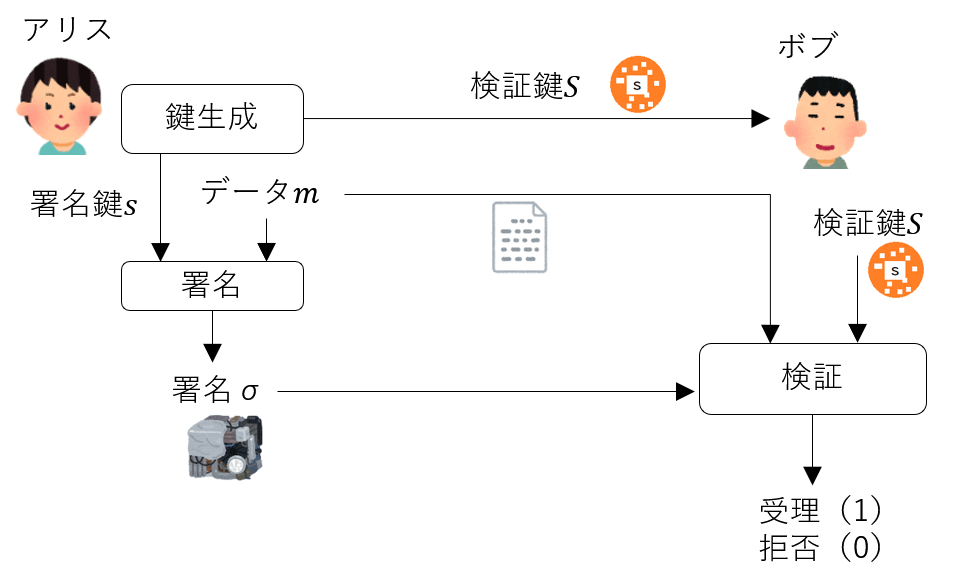
署名

データmと署名σのペアを他人（ボブ）に渡します。
ボブは検証鍵Sを使って(m,σ)の正しさを確認し、受理か拒否します。

ECDSAの鍵生成

ECDSAの鍵生成アルゴリズムは次の通りです。
まずアリスが$\texttt{Fr}$の中から乱数$s$を一つとり、これを署名鍵とします。
そして点$P$を$s$倍した$S=sP$を検証鍵とします。ECDLPの困難性により検証鍵から署名鍵は求まりません。

ECDSA

P = initSecp256k1()
s = Fr()
s.setRand() # 署名鍵
S = P * s   # 検証鍵

鍵生成

ECDSAの署名

署名と検証にはハッシュ関数を使います。ハッシュ関数自体の説明は他の書籍に譲ります。
PythonでSHA-256を使うにはhashlibをimportします。
ハッシュ値は256ビットでPythonでは32個のバイト配列です。
それを有限体$\texttt{Fr}$の値とみなすときは配列の先頭が整数の上位にくるビッグエンディアンとして整数にします。
たとえば$\texttt{b'{\textbackslash}x12{\textbackslash}x34'}$は$\texttt{0x1234}$です。
msgToFr（図中のh）はメッセージmから$\texttt{Fr}$への関数です。

import hashlib
def byteToFr(b):
    v = 0
    for x in b:
        v = v * 256 + x
    return Fr(v)

def msgToFr(msg):
    H = hashlib.sha256()
    H.update(msg)
    return byteToFr(H.digest())

ハッシュ値の整数化

データmの署名を作成するにはまず乱数$k$を選びます。
そして楕円曲線の点$kP$を計算し、その$x$座標を$r$とします。
$\sigma=(r,(h(m)+sr)/k)$が署名です。ここで足し算や割り算は有限体$\texttt{Fr}$を使った計算です。
楕円曲線の点を計算するときは素数$p$を使った有限体でしたが、署名の計算では楕円曲線の点の個数$r$を使った有限体を利用します。

$\texttt{Fp}$と$\texttt{Fr}$は素数が違うだけのクラスです。
どう実装するか悩んだのですが、ここでは安直に$\texttt{fp.py}$をコピーして$\texttt{fr.py}$を作り、クラス名を置換しました。

def sign(P, s, msg):
    z = msgToFr(msg)
    k = Fr()
    k.setRand()
    Q = P * k
    r = Fr(Q.x.v)
    return (r, (r * s + z) / k)

署名

署名に使う乱数

$\texttt{sign}$で使う$k$は正しく乱数を生成しなければなりません。
2010年にPlayStation 3の署名実装が同じ乱数を使っていたため署名鍵が漏洩する脆弱性が見つかりました（Console Hacking 2010 PS3 Epic Fail）。
乱数を生成するのはなかなかやっかいなため、その代わりに署名鍵やデータなどから$k$を生成するアルゴリズムがRFC6979で規定されています。
興味ある方はご覧ください。

ECDSAの検証

最後にverifyを実装します。
verifyは、データmと署名$\sigma=(r,t)$が与えられたときに、まず$\texttt{z=msgToFr(msg)}$を計算します。
そして楕円曲線の点$R=(z P + rS)/t$を計算します。
楕円曲線の点を$t$で割る操作は、有限体$\texttt{Fr}$の中で逆数$w=1/t$を掛けることに相当します。

$$R=(z P + rS)\times w$$

楕円曲線の整数倍は有限体の掛け算に比べてずっと重たい処理なので$R=(zw)P+(rw)S$とすると速くなります。

def verify(P, sig, S, msg):
    (r, t) = sig
    if r == 0 || t == 0:
        return False
    z = msgToFr(msg)
    w = Fr(1) / t
    u1 = z * w
    u2 = r * w
    Q = P * u1 + S * u2
    if Q.isZero:
        return False
    x = Fr(Q.x.v)
    return r == x

検証

最後に求めた楕円曲線の点$Q$の$x$座標が$r$に等しければ$\texttt{True}$を返します。
以上がECDSAの実装です。
実際に使うにはより厳密なチェックや、検証鍵や署名データを相互運用するためのフォーマットなど実装すべき箇所がありますが、手元で数値を確認しながら動作させるにはこれで十分です。
この記事が楕円曲線や鍵共有、署名の理解に少しでも役立てば幸いです。