楕円曲線暗号のPythonによる実装その1（有限体とECDH鍵共有）

お断り

この記事は『Software Design2022年3月号』の「第4章：電子署名のプロセスを体験 Pythonによる楕円曲線暗号の実装」の入稿記事を技術評論社のご好意で公開したものです。
元はLaTeXだったのをマークダウンに修正し、二つに分けています。
記事中のサンプルコードはサポートページからダウンロードできます。

はじめに

この章では楕円曲線を用いた鍵共有や署名をPythonで実装します。実装するために必要な数学は随時解説します。
動作確認はPython 3.8.10で行いました。
コードは動作原理を理解するためのものであり、細かいエラー処理などはしていません。
プロダクト製品などで利用できるものではないことをご了承ください。

用語のおさらい

楕円曲線暗号の位置づけ

まず最初に用語の確認をします。
「暗号」は複数の意味で使われます。
一つは「データを秘匿化するために、他人に読めない形にする暗号化（Encryption）」です。
もう一つは、暗号化だけでなく、鍵共有や署名などの真正性や認証などを含む暗号技術全般を指す暗号（Cryptography）です。
同様に公開鍵暗号も複数の意味で使われ、「公開鍵を使って暗号化し、秘密鍵で復号する」公開鍵暗号PKE（Public Key Encryption）や
「公開情報と秘密情報を組み合わせた暗号技術全般」を指す公開鍵暗号PKC（Public Key Cryptography）などがあります。
両者を区別したいときはPKEを公開鍵暗号方式、PKCを公開鍵暗号技術などということがありますが、確定しているとはいえません。
楕円曲線暗号は英語ではECC（Elliptic Curve Cryptography）といい、楕円曲線EC（Elliptic Curve）を使った暗号技術全般を指します。
TLSやSSH、FIDO2、ブロックチェーンなどでは楕円曲線を使った鍵共有や署名が使われます。

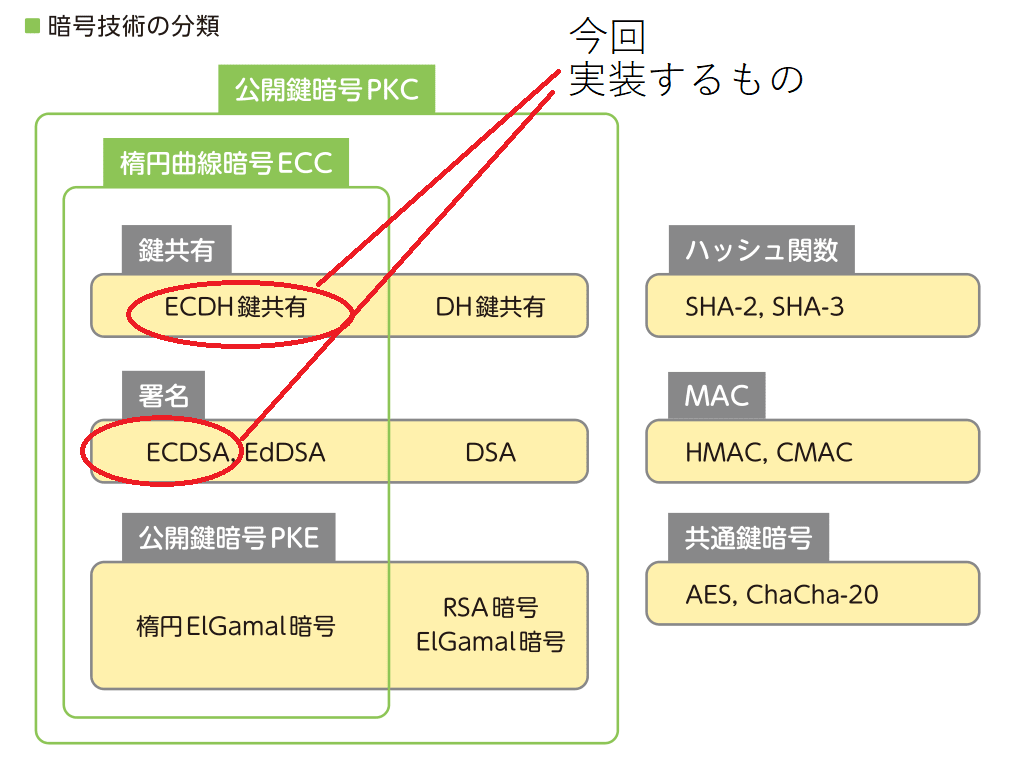
暗号技術の分類（『暗号と認証のしくみと理論がこれ1冊でしっかりわかる教科書』p.168より引用）

意外かもしれませんが身近なところで楕円曲線が「暗号化」を意味する公開鍵暗号PKEで使われることはほとんどありません。
CRYPTREC（CRYPTography Research and Evaluation Committees）が提示している電子政府推奨暗号リストを見ても、公開鍵暗号の守秘（暗号化）で推奨されているのはRSA暗号ベースのRSA-OAEPだけで楕円曲線ベースのものはありません。
楕円曲線を使った署名の説明で「暗号化」の言葉が出てきたらそれは通常間違っているのでご注意ください。
この章で実装するのは鍵共有と署名です。

DH鍵共有

前章で説明されたDH鍵共有をPythonを使いながら復習します。
アリスとボブで鍵共有をする場合、あらかじめ利用する素数$p$と整数$g$を決めておきます。
ここでは$p=65537$と$g=3$としましょう。
そしてアリスとボブがそれぞれ秘密の値$a$と$b$をランダムに選びます。
Pythonでは$\texttt{secrets.randbelow(p)}$で$0$以上$p$未満の乱数を取得できます。
$\texttt{secrets}$は暗号学的に安全な乱数を生成するモジュールです。

次にアリスとボブはそれぞれ$A=g^a \mod{p}$と$B=g^b \mod{p}$を計算します。$\mod{p}$は$p$で割った余りを表します。
掛け算やベキ乗の$\mod{p}$を求めるのは容易です。
Pythonでは$\texttt{pow(g, a, p)}$を使うと$A$を計算できます。$\texttt{pow}$の第3引数はその数で割った余りを求めます。

アリスが$A$をボブに、ボブが$B$をアリスに渡して$s_1=B^a \mod{p}$と$s_2=A^b \mod{p}$を計算するとそれらが一致することで鍵共有が行われるのでした。

import secrets
p = 65537
g = 3
a = secrets.randbelow(p)
b = secrets.randbelow(p)
print("a =", a)
print("b =", b)
A = pow(g, a, p)
B = pow(g, b, p)
print("A =", A)
print("B =", B)
s1 = pow(B, a, p)
s2 = pow(A, b, p)
print("s1 =", s1)
print("s2 =", s2)
print("s1 == s2?", s1 == s2)

DH鍵共有

a = 37562
b = 4823
A = 64643
B = 38750
s1 = 59475
s2 = 59475
s1 == s2? True

実行例（実行する度変わります）

DH鍵共有の安全性

DH鍵共有の通信を盗聴している攻撃者は素数$p$や整数$g$と$A$や$B$も入手できます。
したがってまず$g$と$p$と$A=g^a \mod{p}$から秘密の値$a$が求められては困ります。
この性質を離散対数問題DLP（Discrete Logarithm Problem）の困難性といいます。

次にDLPが解けなくても$g$と$p$と$A$と$B$から$g^{ab} \mod{p}$が求められても困ります。
この性質をDH問題DHP（DH Problem）の困難性といいます。
安全にDH鍵共有をするにはDHPの困難性が求められます。

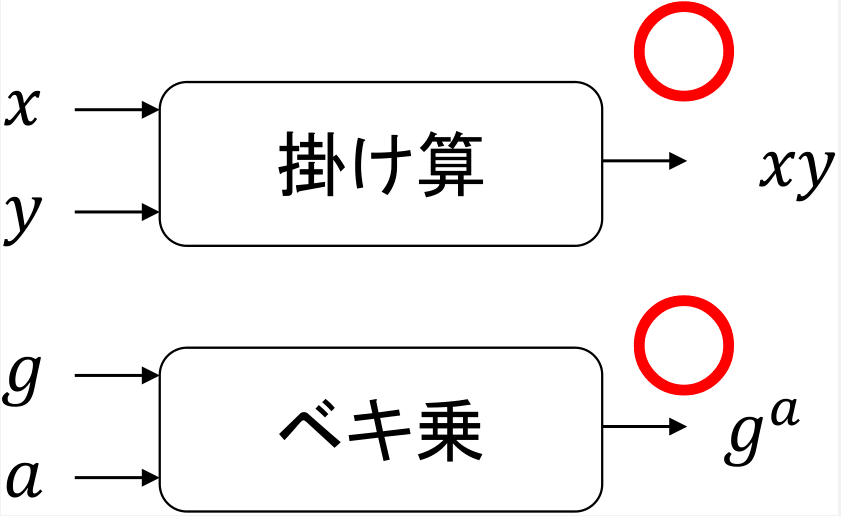
ベキ乗（${} \mod{p}$は省略）

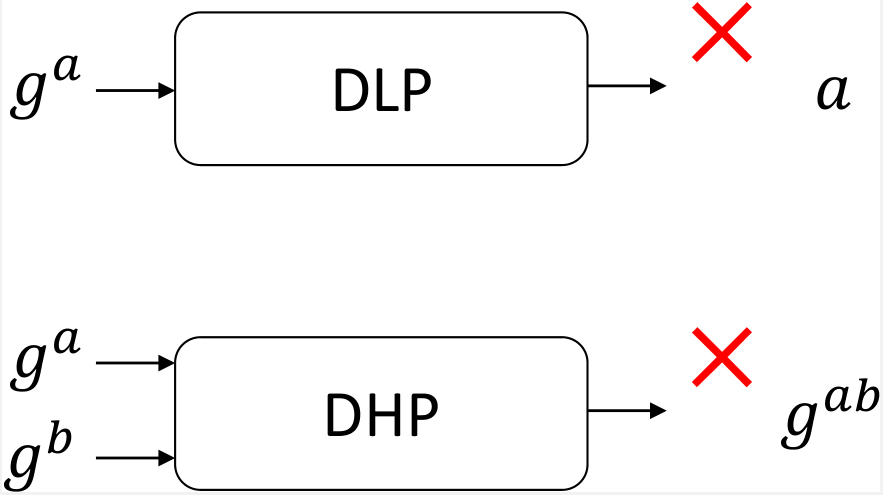
DLPとDHP

楕円曲線暗号

楕円曲線

前節で紹介したようにDH鍵共有はDLPやDHPなどの困難性を利用した方式でした。
似た性質を持つ困難性があれば、それを利用して暗号を作れる可能性があります。
その一つが近年普及している楕円曲線です。

楕円曲線のイメージは浮輪の表面（これをトーラスと言います）です。
そのトーラスには糸が巻きついていて、$r$個の$O$, $P$, $2P$, $3P$, ..., $(r-1)P$という印（点）があります。
$rP$は$O$に戻って巻きついた糸は一つの輪になっています。
そしてこれらの点に対して$aP + bP = (a+b \pmod{r})P$という演算が定義されています（$a$, $b$は整数）。

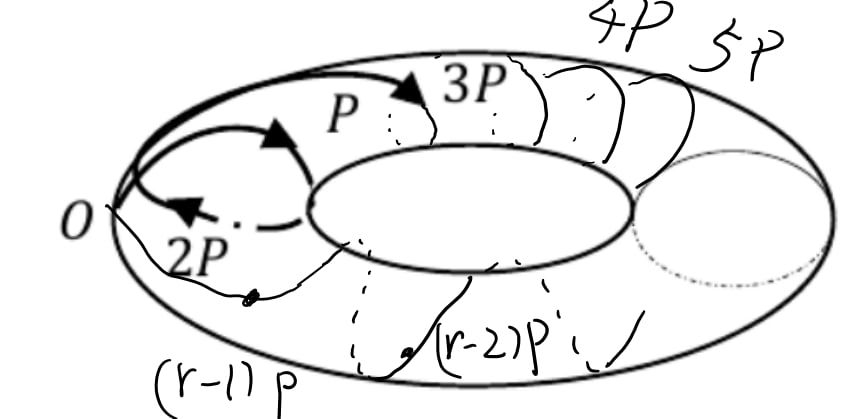
楕円曲線とその上の点

ECDLPとECDHP

楕円曲線上でDLPやDHPに相当する問題を考えます。
DLPやDHPは掛け算やベキ乗算で表現されていましたが、楕円曲線上では点の足し算や整数倍で表現します。

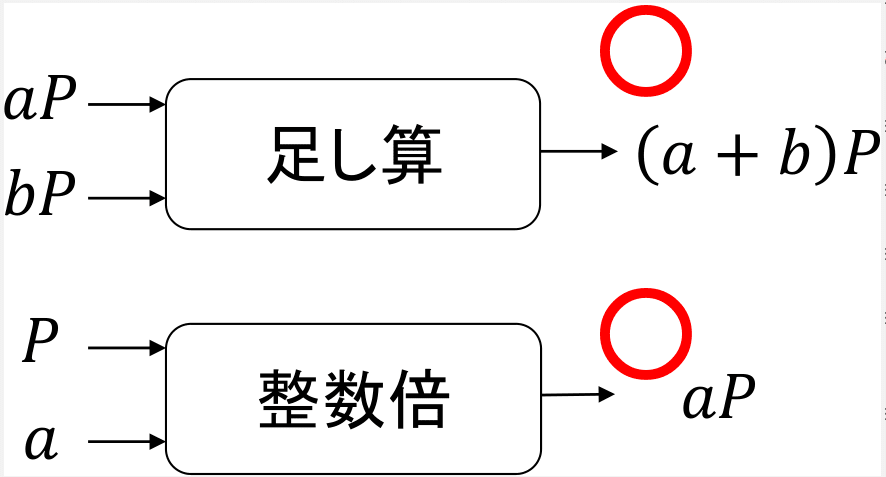
楕円曲線の点の演算

点$P$と$aP$が与えられたときに$a$を求める問題を楕円離散対数問題ECDLPといいます。
同様に$P$と$aP$と$bP$が与えられたときに$abP$を求める問題を楕円DH問題ECDHPといいます。

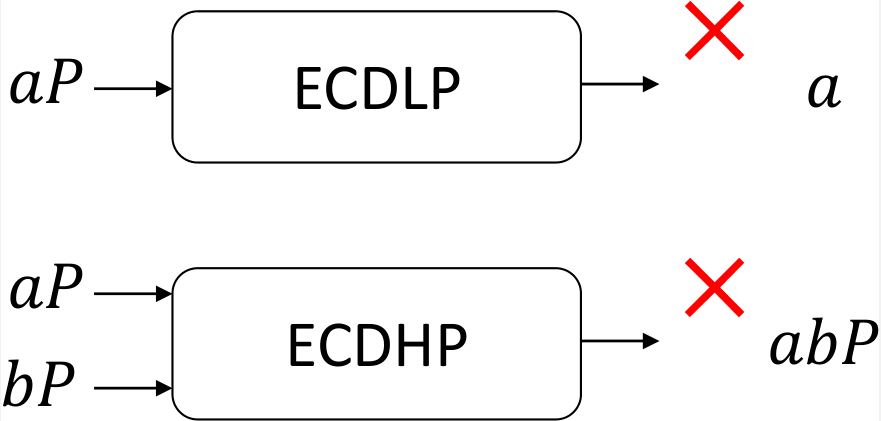
ECDLPとECDHPの困難性

楕円曲線のパラメータを適切に取るとECDLPやECDHPが困難であることが知られています。
楕円曲線を使うと今までのDH鍵共有に比べてずっと少ないビット長でより高い安全性を達成できます。
具体的には2048ビットの素数のDH鍵共有よりも256ビットの楕円曲線を使ったDH鍵共有の方が安全です。

ECDH鍵共有

ECDHPが困難という仮定の元で、楕円曲線版のDH鍵共有ができます。これをECDH鍵共有といいます。

1. アリスが乱数$a$を選び$aP$をボブに送る。
2. ボブが乱数$b$を選び$bP$をアリスに送る。
3. アリスは$a(bP)=abP$を計算する。
4. ボブは$b(aP)=abP$を計算する。

$abP=baP$が成り立つので秘密の値$abP$を共有でき、それからAESなどの秘密鍵を作ります。

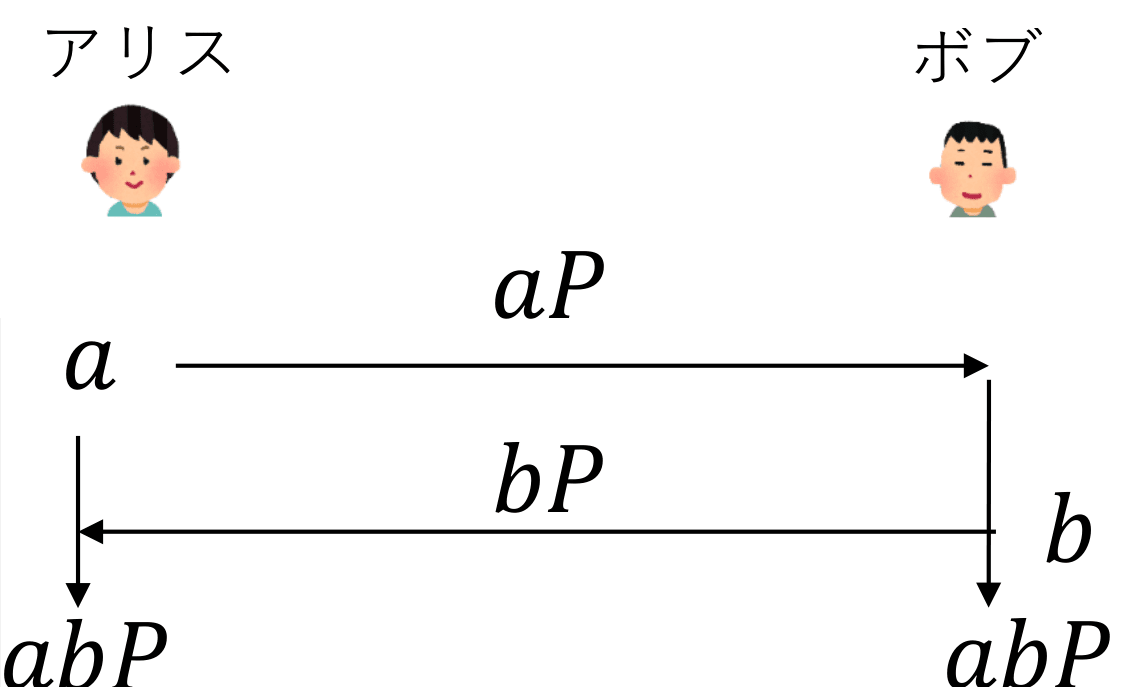
ECDH鍵共有

楕円曲線の実装

ECDH鍵共有の例

まず全体像を把握するために、楕円曲線クラス$\texttt{Ec}$を使ったECDH鍵共有の例を見ましょう。

詳細は後述しますが、楕円曲線の点は2個の整数の組$(x, y)$で表され、点同士の加減算や整数倍のメソッドがあります。
サンプルの中で$\texttt{Fr}$は素数$r$未満の整数を表します。
$\texttt{initSecp256k1()}$で楕円曲線でよく使われるsecp256k1というパラメータで初期化します。
関数の戻り値は楕円曲線の点です。

そして、$\texttt{Fr.setRand()}$というメソッドで乱数を1個選びます。
内部ではECDH鍵共有の節で紹介した$\texttt{secrets.randbelow}$を呼んでいるだけです。

$\texttt{aP = P * a}$が楕円曲線の点を秘密の値$a$倍するアリスの作業、$\texttt{bP = P * b}$が$b$倍するボブの作業です。
そのあと、アリスが$aP$を、ボブが$bP$を相手に渡し、$\texttt{abP = bP * a}$でアリスが$abP$を、$\texttt{baP = aP * b}$でボブが$baP$を計算しています。
最後にそれぞれの値を表示して$abP == baP$を確認しています。

from ec import Ec, Fr
from ec import initSecp256k1

P = initSecp256k1()
a = Fr()
b = Fr()
a.setRand()
b.setRand()
print(f"a={a}")
print(f"b={b}")
aP = P * a
bP = P * b
baP = aP * b
abP = bP * a
print(f"baP={baP}")
print(f"abP={abP}")
print(f"baP == abP? {baP == abP}")

ECDH鍵共有の例

a=0x374a3960204d5170e615181dec9f8b40810a88f81af9f66e8bc096260beb1444
b=0x1ba9a286dcfbb544fd2ba4d163a1a6dc8bdb3eecbe08779082aa8052194cc129
baP=(0x6c86ae1d8a0b3e0311c02064668854687d4fc00e6c642716669cf6ce7ac97f76, 0xed9e0d8d69dce6be8702769547ba9edc693bb18e026d09f811a5f96598a51aa9)
abP=(0x6c86ae1d8a0b3e0311c02064668854687d4fc00e6c642716669cf6ce7ac97f76, 0xed9e0d8d69dce6be8702769547ba9edc693bb18e026d09f811a5f96598a51aa9)
baP == abP? True

ECDH鍵共有の結果

楕円曲線クラスの使い方が伝わったでしょうか。

有限体

さて、これからいよいよ楕円曲線の実装に入ります。
そのためには有限体（ゆうげんたい）という概念が必要です。

四則演算ができる集合を体（たい）といいます。
分数（有理数）の集合や実数の集合は四則演算の結果も分数や実数です。そのため有理数体や実数体といいます。
今回扱うのは有限個の集合からなる体なので有限体といいます。

従来のDH鍵共有では掛け算やベキ乗算のあとに$p$で割っていました。
ここでは素数$p$で割った余りの集合$\{0, 1, 2, ..., p-1\}$に四則演算を導入して有限体にしたものを有限体クラス$\texttt{Fp}$とします。

有限体の加減乗算

有限体クラスは素数$p$をクラス変数として持ちます。その値を設定するメソッドを$\texttt{init(p)}$としましょう。

class Fp:
    @classmethod
    def init(cls, p):
        cls.p = p

有限体クラスの初期化

四則演算のうち、足し算、引き算、掛け算は普通に演算をした後$p$で割ればよいので簡単です。
メンバ変数はvとしましょう。

class Fp:
    ...
    # 値を設定する
    def __init__(self, v=0):
        self.v = v % Fp.p
    def __add__(self, rhs):
        return Fp(self.v + rhs.v)
    def __sub__(self, rhs):
        return Fp(self.v - rhs.v)
    def __mul__(self, rhs):
        return Fp(self.v * rhs.v)

有限体クラスのadd, sub, mul

有限体の除算

有限体の割り算はちょっと頭をひねります。
整数$a$の普通の逆数は$1/a$なので分数となり、整数で表せないからです。
そのためこの方法では体になりません。

そこで割り算の定義を少し変えます。
$X=1/a$というのは$(a \times X) \mod{p} = 1$ということなので、「$a$に掛けて$p$で割った余りが1になる整数」$X$を$a$の逆数と考えます。
たとえば$p=7$, $a=3$のとき、$3 \times 5 = 15 \equiv 1 \pmod{7}$なので$X=1/3=5$とみなすのです。

このような$X$を探す方法はいくつかありますが、ここではフェルマーの小定理を使います。
フェルマーの小定理とは素数$p$と1以上$p$未満の整数$a$に対して$a$を$p-1$乗して$p$で割ったら余りは1になるという定理：

$$a^{p-1} \equiv 1 \pmod{p}$$

です。RSA暗号で登場するのでご存じの方もいらっしゃるかもしれません。ここではこの定理を認めて先に進めます。
$p>2$のとき、この式を

$$a (a^{p-2}) \equiv 1 \pmod{p}$$

と変形します。$X=a^{p-2}$とすると、これは$aX \equiv 1 \pmod{p}$を意味します。
つまり$X$は$a$の逆数と思えるのです。
Pythonでは$X$は$\texttt{pow(a, p-2, p)}$で計算できました。
0の逆数は普通の数と同じく存在しないのでエラーにします。

def inv(self):
    v = self.v
    if v == 0:
        raise Exception("zero inv")
    p = Fp.p
    return Fp(pow(v, p-2, p))

有限体クラスのinv

逆数ができれば割り算$\texttt{a / b}$は$\texttt{a * (1/b)}$で計算できます。

def __truediv__(self, rhs):
    return self * rhs.inv()

有限体クラスの除算

実際に$p=7$のとき$\texttt{1 * (5/1) = 5, 2 * (5/2) = 5, 3 * (5/3) = 5, ...}$となることを確認してみましょう。

from fp import Fp

p = 7
Fp.init(p)
a = Fp(5)
for i in range(1, p):
    x = Fp(i)
    r = a / x
    print(f"{x}*{r}={x*r}")

除算の例

0x1*0x5=0x5
0x2*0x6=0x5
0x3*0x4=0x5
0x4*0x3=0x5
0x5*0x1=0x5
0x6*0x2=0x5

除算の例の結果

期待する結果になっています（楕円曲線暗号のPythonによる実装その2（楕円曲線とECDSA）に続く）。