概要
前回はオフポリシーの線形関数近似として\overline{VE}が利用できないことを示し、\overline{PBE}が有効であることが紹介された。
今回は主に
-
\overline{PBE}の導出の途中にあった\overline{BE}をなぜ使わないのか
-
\overline{PBE}を目的関数としたSGD
を紹介する。
11.5 Stochastic Gradient Descent in the Bellman Error
- オフポリシーの半勾配法は一般的には収束が保証されておらず、前回の例では発散するケースがあることがわかった。
- 勾配法(SGD)であれば収束が保証されているが、\overline{VE}を目的関数とする場合はMC法でしか実現できない
- MC法では時間がかかりすぎることがある。
- そこで一般的に提案されているベルマン誤差に基づく目的関数を導入したい。
- 次からはベルマン誤差に基づく学習の起源と限界を示す。
Mean Squared TD Error
ベルマン誤差に基づく学習の前にTD誤差に基づく学習について考える。
TD誤差は、#11で定義したように、
\delta_{t}=R_{t+1}+\gamma \hat{v}\left(S_{t+1}, \mathbf{w}_{t}\right)-\hat{v}\left(S_{t}, \mathbf{w}_{t}\right)
で表される。 このTD誤差の二乗の期待値が平均平方TD誤差(Mean Squared TD Error)であり、オフポリシーでは、
\begin{aligned}
\overline{\operatorname{TDE}}(\mathbf{w}) &=\sum_{s \in \mathcal{S}} \mu(s) \mathbb{E}\left[\delta_{t}^{2} \mid S_{t}=s, A_{t} \sim \pi\right] \\
&=\sum_{s \in \mathcal{S}} \mu(s) \mathbb{E}\left[\rho_{t} \delta_{t}^{2} \mid S_{t}=s, A_{t} \sim b\right] \\
&=\mathbb{E}_{b}\left[\rho_{t} \delta_{t}^{2}\right]
\end{aligned}
のように表される。SGDではこの期待値の部分をサンプリングすることで解決するので、
\begin{aligned}
\mathbf{w}_{t+1} &=\mathbf{w}_{t}-\frac{1}{2} \alpha \nabla\left(\rho_{t} \delta_{t}^{2}\right) \\
&=\mathbf{w}_{t}-\alpha \rho_{t} \delta_{t} \nabla \delta_{t} \\
&=\mathbf{w}_{t}+\alpha \rho_{t} \delta_{t}\left(\nabla \hat{v}\left(S_{t}, \mathbf{w}_{t}\right)-\gamma \nabla \hat{v}\left(S_{t+1}, \mathbf{w}_{t}\right)\right)
\end{aligned}
として更新すれば、TD誤差のSGDが達成される。
ただし、\muはb(behavior policy)のもとサンプリングされた分布をさす。
ここで#16で示したsemi-gradient TD(0)と比較すると、最後の項に引き算が追加されたことがわかる。
この項の存在によって収束が保証される(証明?)。
このアルゴリズムを単純残差勾配アルゴリズム(naive residual-gradient algorithm)と呼ぶ。
しかし、この方法はロバストに収束するものの、最適解に収束する保証はない。
以下がその例である。
A-split Example
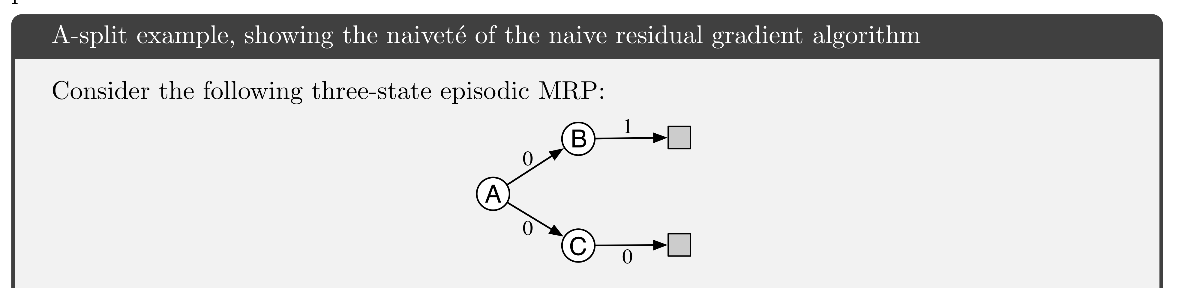
上の図のように、Aからエピソードが始まって、確率1/2報酬0でBへ、確率1/2報酬0でCへ遷移し、Bからは確率1報酬1で終端に、Cからは確率1報酬0で終端に遷移するマルコフ報酬過程(MRP)を考える。
真の状態価値は、
- v(A) = 1/2
- v(B) = 1
- v(C) = 0
であるが、仮に正しく推定できたとき、\gamma=1のTD誤差は
1ステップ目:
1/2・(0 + v(B) - v(A))^2 + 1/2・(0 + v(C) - v(A))^2 = 1/4
2ステップ目:
1/2・(1 - v(B))^2 + 1/2・(0 - v(C))^2 = 0
となるため、\overline{TDE} = 1/8と計算できる。
しかし、推定値:
-
\hat{v}(A) = 1/2
-
\hat{v}(B) = 3/4
-
\hat{v}(C) = 1/4
とすると、\gamma=1のTD誤差は、
1ステップ目:
1/2・(0 + \hat{v}(B) - \hat{v}(A))^2 + 1/2・(0 + \hat{v}(C) - \hat{v}(A))^2 = 1/16
2ステップ目:
1/2・(1 - \hat{v}(B))^2 + 1/2・(0 - \hat{v}(C))^2 = 1/16
となって、\overline{TDE} = 1/16となる。
つまり、誤った推定値の方が正しい推定値よりも誤差が小さいとされてしまう。
ベルマン誤差
これに対応する一つの方法がベルマン誤差最小化による学習である。仮に完全に正しい推定値を得ているのであればベルマン誤差は0となるので、A-splitのような問題は起きない。一般にベルマン誤差は0になることはないが、それは表現可能な空間に真の推定値が存在しないことを意味するので、理想に近づけようとすることは自然な発想である。
(復習)
#20で導出した通り、ある状態におけるベルマン誤差はターゲットポリシーに関する期待値であった。
\begin{aligned}
\bar{\delta}_{\mathbf{w}}(s) & \doteq\left(\sum_{a} \pi(a \mid s) \sum_{s^{\prime}, r} p\left(s^{\prime}, r \mid s, a\right)\left[r+\gamma v_{\mathbf{w}}\left(s^{\prime}\right)\right]\right)-v_{\mathbf{w}}(s) \\
&=\mathbb{E}\left[R_{t+1}+\gamma v_{\mathbf{w}}\left(S_{t+1}\right)-v_{\mathbf{w}}\left(S_{t}\right) \mid S_{t}=s, A_{t} \sim \pi\right]
\end{aligned}
また、平均平方ベルマン誤差(\overline{BE}, Mean Squared Bellman Error)は、
各状態のベルマン誤差の\muに関する重み付きノルムで、
\overline{BE}(w) = \| \bar{\delta}_w \|^2_{\mu}
である。
(復習終わり)
よって、このベルマン誤差を最小化するSGDは、
\begin{aligned}
\mathbf{w}_{t+1} &=\mathbf{w}_{t}-\frac{1}{2} \alpha \nabla\left(\mathbb{E}_{\pi}\left[\delta_{t}\right]^{2}\right) \\
&=\mathbf{w}_{t}-\frac{1}{2} \alpha \nabla\left(\mathbb{E}_{b}\left[\rho_{t} \delta_{t}\right]^{2}\right) \\
&=\mathbf{w}_{t}-\alpha \mathbb{E}_{b}\left[\rho_{t} \delta_{t}\right] \nabla \mathbb{E}_{b}\left[\rho_{t} \delta_{t}\right] \\
&=\mathbf{w}_{t}-\alpha \mathbb{E}_{b}\left[\rho_{t}\left(R_{t+1}+\gamma \hat{v}\left(S_{t+1}, \mathbf{w}\right)-\hat{v}\left(S_{t}, \mathbf{w}\right)\right)\right] \mathbb{E}_{b}\left[\rho_{t} \nabla \delta_{t}\right] \\
&=\mathbf{w}_{t}+\alpha\left[\mathbb{E}_{b}\left[\rho_{t}\left(R_{t+1}+\gamma \hat{v}\left(S_{t+1}, \mathbf{w}\right)\right)\right]-\hat{v}\left(S_{t}, \mathbf{w}\right)\right]\left[\nabla \hat{v}\left(S_{t}, \mathbf{w}\right)-\gamma \mathbb{E}_{b}\left[\rho_{t} \nabla \hat{v}\left(S_{t+1}, \mathbf{w}\right)\right]\right]
\end{aligned}
のような更新によって達成されることがわかる。この更新とそれをサンプリングする様々な方法は、残差勾配アルゴリズムと呼ばれる。期待値を単純にサンプル値から算出した場合は単純残差勾配アルゴリズムと一致する。
ここで、積についてバイアスのないサンプルを得るためには、2つの独立したサンプルが必要である。そのため、外部環境との相互作用での場合不可能な方法となる。
残差勾配アルゴリズムは、
の場合、実行可能である。それは、
- 決定論的であれば、2つのサンプルは必然的に同じになる。
- シミュレートされた環境であれば、Stから次の状態であるSt+1を2つの独立にサンプルを得られる。
ためである。
この方法は、ロバストに、
に収束することがわかっている。(証明?)
しかし、残差勾配法の問題は少なくとも3つ残っている。
- 経験的に遅い
- 依然として間違った値に収束してしまうことがある(非線形)
- 学習不可能である。
計算スピード
最初はより高速な半勾配法と組み合わせて速度を上げ、収束を保証するために徐々に残差勾配法に切り替えることを提案もある (Baird and Moore, 1999)。
非最適性
以下のA-presplit例はBEを最小化することが望ましい値が得られないことを表している。
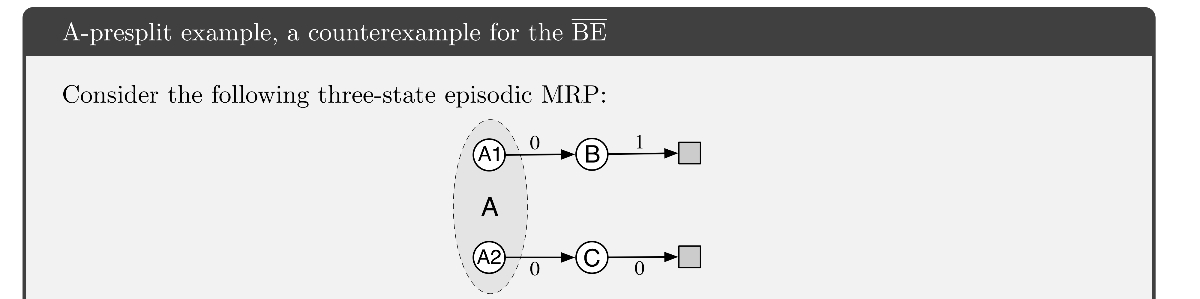
A-splitに対して、エピソードの視点をA1, A2と分割させ、決定的に遷移する状況を考える。
ただし、エピソードの始点はA1,A2を1/2の確率で選択する。
また、状態集約によって関数近似してA1, A2は同じパラメータによって価値が決まるとする。
このような例でもやはり
-
\hat{v}(A) = 1/2
-
\hat{v}(B) = 3/4
-
\hat{v}(C) = 1/4
に収束してしまう。(関数近似によって\overline{BE} = 0が、表現可能な空間に存在しないため)
- A-splitは解決できたが、ほぼ同等な(決定的な要素と状態集約を追加した)A-presplitでは問題を解決できていない。
11.6 The Bellman Error is Not Learnable
学習不可能性
機械学習系で学習可能とは、多項式時間の間に許容可能な解を見つけられることを言う。
しかし、ここでは無限のデータ(経験)量と無限の計算時間があれば、環境や状態価値などの内部構造できるのか否かのことを指す(ことにする)。
その意味で目的関数を\overline{BE}とする方法は学習可能でない。
以下のMRPの例でそれが確認できる。
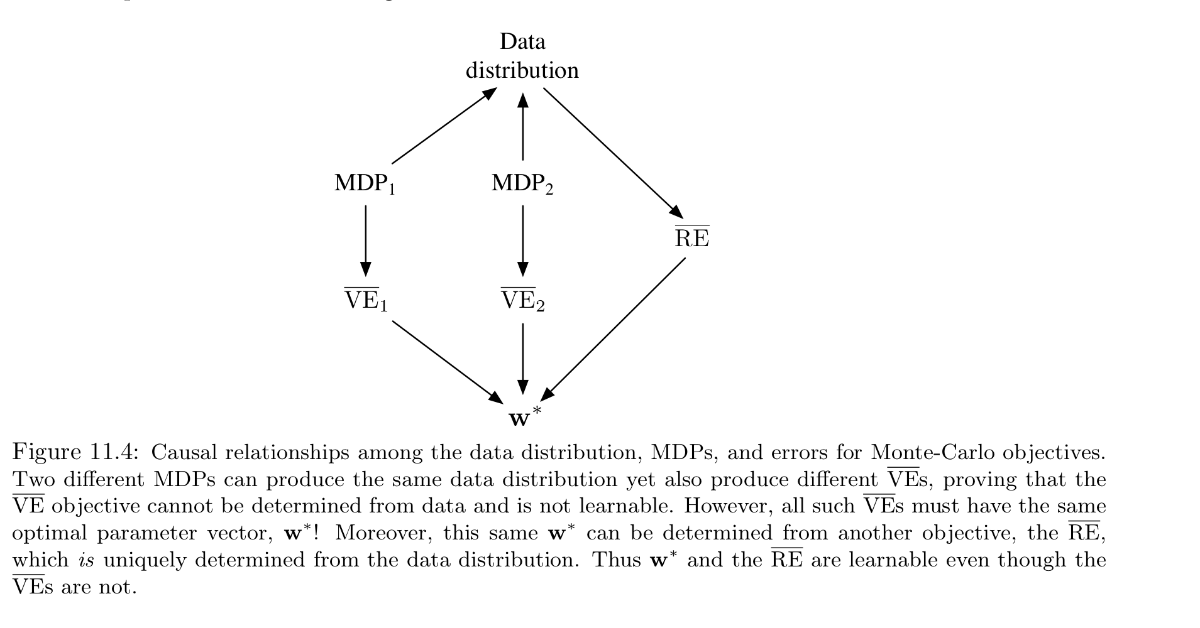
\overline{VE}
まず、目的関数\overline{VE}について見ていく。

上の図で各状態からの矢印は等確率で遷移する方向を意味し、数字が報酬である。
wはその状態価値を表し、右のMRPでは状態集約されて一つの値で表される。
真の状態価値は左から1,0,2であり、左右どちらの図でもwの最適値は1である。
しかし、ここでw=1のときの\overline{VE}を考えると、左の場合で0, 右の場合で1となる。
これより\overline{VE}が学習不可能であることがわかる。
つまり、どれだけデータがあっても、どちらのMRPかは見分けられず、\overline{VE}の最適値はわからない。
しかし、VEの場合、最適値は一致しないものの、最適解は一致している。この仕組みは目的関数\overline{RE}を見ればわかる。\overline{RE}は平均平方報酬誤差(Mean Squared Return Error)で、
\begin{aligned}
\overline{\mathrm{RE}}(\mathbf{w}) &=\mathbb{E}\left[\left(G_{t}-\hat{v}\left(S_{t}, \mathbf{w}\right)\right)^{2}\right] \\
&=\overline{\mathrm{VE}}(\mathbf{w})+\mathbb{E}\left[\left(G_{t}-v_{\pi}\left(S_{t}\right)\right)^{2}\right]
\end{aligned}
のように表される。ただし、期待値は\mu, pについて。
これより、\overline{RE}は\overline{VE}に、パラメータwに依存しない推定値の分散を足したものであるとわかる。つまり、MRPの構造から推定値の分散(定数項)が決定しており、パラメーターに依存する部分は結果として同じであったため最適解が同じとなったことがわかる。つまり、\overline{VE}は学習不可能であるものの、最適解のみが欲しい状況であれば有効である。
\overline{BE}
次に、\overline{BE}を見ていく。
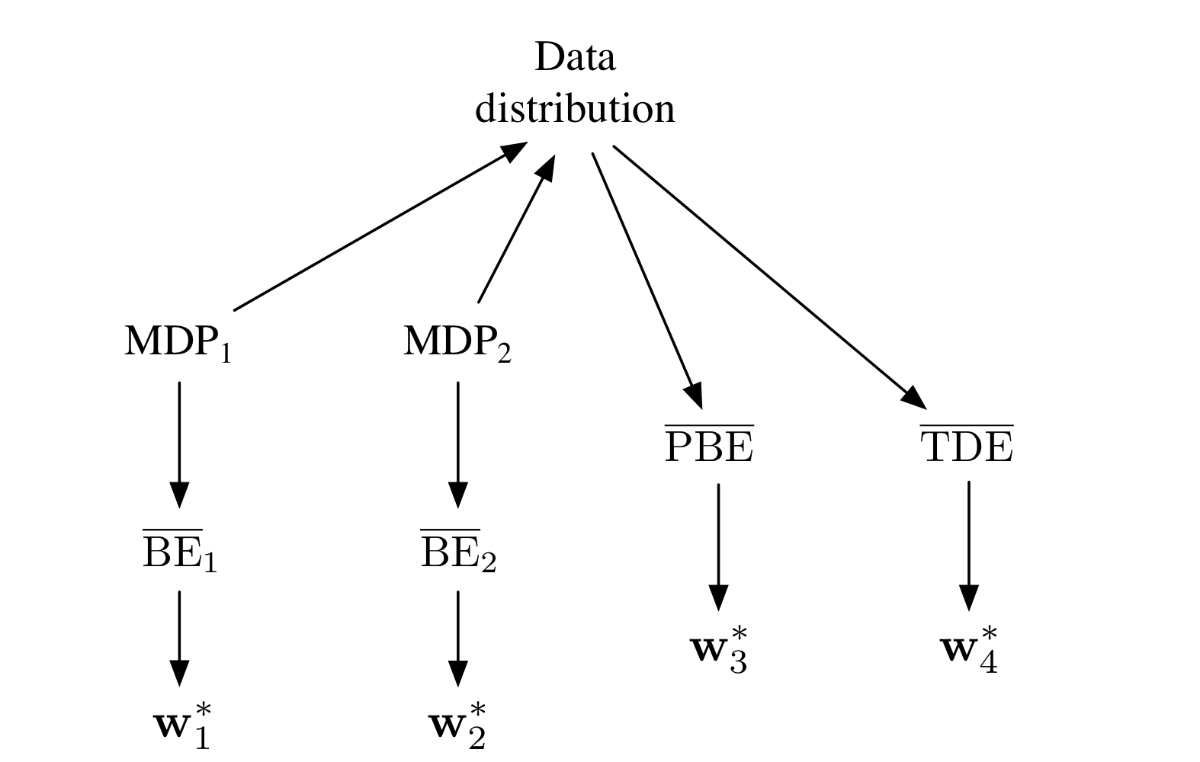
\overline{BE}は同じく\overline{VE}と同じくデータ無限にあってもその最適値を求めることができない。また、\overline{VE}と異なり、最適解も求められない。
次の例は同じ分布のデータを生成するものの異なる解を見つけてしまう例である。

- 左のMRPは、二つの状態にそれぞれ状態価値をもち、
- 右のMRPはAとB,B'にそれぞれ状態価値を持ち、
それをwとすると、二つのMRPのデータの分布は一致する。
左のMRPは明らかに最適解はw = 0で、最適値も0である。
しかし、右のMRPでw=0のとき\overline{BE}を計算すると、
- Aについての平均TD誤差 = 0
- Bについての平均TD誤差 = 1
- B'についての平均TD誤差 = 1
- \mu(A) = 1/3
- \mu(B) = 1/3
- \mu(B') = 1/3
より、$\overline{BE} = 2/3 $ となり、やはり最適値が一致しない。
さらに、w = (-1/2, 0)について右のMRPで\overline{BE}を計算すると、
- Aについての平均TD誤差 = 1/2
- Bについての平均TD誤差 = 1/2
- B'についての平均TD誤差 = -1
より、$\overline{BE} = 1/2 $ と計算でき、最適解も一致しない。
一般的には次の図で表される。
11.7 Gradient-TD Methods
線形の真のSGD(gradient method)はオフポリシーであっても(MC法などでunbiased estimatorを用いれば)w_{TD}に収束するアルゴリズムであったが、逆行列の計算によりO(d^2)となり時間がかかりすぎる。ここでは\overline{PBE}の勾配法の具体的なアルゴリズムを導出し、O(d)で達成できることを確認する。
\begin{aligned}
\overline{\mathrm{PBE}}(\mathbf{w}) &=\left\|\Pi \bar{\delta}_{\mathbf{w}}\right\|_{\mu}^{2} \\
&=\left(\Pi \bar{\delta}_{\mathbf{w}}\right)^{\top} \mathbf{D} \Pi \bar{\delta}_{\mathbf{w}} \\
&=\bar{\delta}_{\mathbf{w}}^{\top} \Pi^{\top} \mathbf{D} \Pi \bar{\delta}_{\mathbf{w}} \\
&=\bar{\delta}_{\mathbf{w}}^{\top} \mathbf{D} \mathbf{X}\left(\mathbf{X}^{\top} \mathbf{D} \mathbf{X}\right)^{-1} \mathbf{X}^{\top} \mathbf{D} \bar{\delta}_{\mathbf{w}}\\
&=\left(\mathbf{X}^{\top} \mathbf{D} \bar{\delta}_{\mathbf{w}}\right)^{\top}\left(\mathbf{X}^{\top} \mathbf{D} \mathbf{X}\right)^{-1}\left(\mathbf{X}^{\top} \mathbf{D} \bar{\delta}_{\mathbf{w}}\right)
\end{aligned}
ただし、
- 1→3行目は重み付きノルムの定義より、
- 3→4行目は\Pi^{\top} \mathbf{D} \Pi=\mathbf{D} \mathbf{X}\left(\mathbf{X}^{\top} \mathbf{D} \mathbf{X}\right)^{-1} \mathbf{X}^{\top} \mathbf{D}より
これより、\overline{PBE}のwに関する勾配は、
\nabla \overline{\mathrm{PBE}}(\mathbf{w})=2 \nabla\left[\mathbf{X}^{\top} \mathbf{D} \bar{\delta}_{\mathbf{w}}\right]^{\top}\left(\mathbf{X}^{\top} \mathbf{D} \mathbf{X}\right)^{-1}\left(\mathbf{X}^{\top} \mathbf{D} \bar{\delta}_{\mathbf{w}}\right)
となる。まず、積で表された、両端の項について
\mathbf{X}^{\top} \mathbf{D} \bar{\delta}_{\mathbf{w}}=\sum_{s} \mu(s) \mathbf{x}(s) \bar{\delta}_{\mathbf{w}}(s)=\mathbb{E}\left[\rho_{t} \delta_{t} \mathbf{x}_{t}\right]
と表せる。さらに、TD誤差の定義より
\begin{aligned}
\nabla \mathbb{E}\left[\rho_{t} \delta_{t} \mathbf{x}_{t}\right]^{\top} &=\mathbb{E}\left[\rho_{t} \nabla \delta_{t}^{\top} \mathbf{x}_{t}^{\top}\right] \\
&=\mathbb{E}\left[\rho_{t} \nabla\left(R_{t+1}+\gamma \mathbf{w}^{\top} \mathbf{x}_{t+1}-\mathbf{w}^{\top} \mathbf{x}_{t}\right)^{\top} \mathbf{x}_{t}^{\top}\right] \\
&=\mathbb{E}\left[\rho_{t}\left(\gamma \mathbf{x}_{t+1}-\mathbf{x}_{t}\right) \mathbf{x}_{t}^{\top}\right]
\end{aligned}
である。また、積で表される中央の項は、
\mathbf{X}^{\top} \mathbf{D} \mathbf{X}=\sum_{s} \mu(s) \mathbf{x}_{s} \mathbf{x}_{s}^{\top}=\mathbb{E}\left[\mathbf{x}_{t} \mathbf{x}_{t}^{\top}\right]
であるから、
\nabla \overline{\mathrm{PBE}}(\mathbf{w})=2 \mathbb{E}\left[\rho_{t}\left(\gamma \mathbf{x}_{t+1}-\mathbf{x}_{t}\right) \mathbf{x}_{t}^{\top}\right] \mathbb{E}\left[\mathbf{x}_{t} \mathbf{x}_{t}^{\top}\right]^{-1} \mathbb{E}\left[\rho_{t} \delta_{t} \mathbf{x}_{t}\right]
と変形できる。このように表せばSGDによって更新できるように思われるが、全ての期待値の項を同じサンプリングによって計算するとバイアスが生じる。(残差勾配法と同様)
そこで、3つ別々にサンプリングして期待値をとるということも考えられるが、特に、中央の項では逆行列を取らなくてはならず、計算時間がかかり過ぎてしまう。(インクリメンタルに逆行列をとってもO(d^2))
そこで、
\mathbf{v} \approx \mathbb{E}\left[\mathbf{x}_{t} \mathbf{x}_{t}^{\top}\right]^{-1} \mathbb{E}\left[\rho_{t} \delta_{t} \mathbf{x}_{t}\right]
と表して、w,vを別々に推定することで独立性を保つ方法を考える。(これは残差勾配法でも使用される)
すると、vの推定値は線形の教師あり機械学習と同じ重み付きのLMS(Least Mean Square)に基づく更新と同じことがわかり、
\mathbf{v}_{t+1}=\mathbf{v}_{t}+\beta \rho_{t}\left(\delta_{t}-\mathbf{v}_{t}^{\top} \mathbf{x}_{t}\right) \mathbf{x}_{t}
として毎ステップ更新が行える。
このvを用いれば、
\begin{aligned}
\mathbf{w}_{t+1} &=\mathbf{w}_{t}-\frac{1}{2} \alpha \nabla \overline{\mathrm{PBE}}\left(\mathbf{w}_{t}\right) \\
&=\mathbf{w}_{t}-\frac{1}{2} \alpha 2 \mathbb{E}\left[\rho_{t}\left(\gamma \mathbf{x}_{t+1}-\mathbf{x}_{t}\right) \mathbf{x}_{t}^{\top}\right] \mathbb{E}\left[\mathbf{x}_{t} \mathbf{x}_{t}^{\top}\right]^{-1} \mathbb{E}\left[\rho_{t} \delta_{t} \mathbf{x}_{t}\right] \\
&=\mathbf{w}_{t}+\alpha \mathbb{E}\left[\rho_{t}\left(\mathbf{x}_{t}-\gamma \mathbf{x}_{t+1}\right) \mathbf{x}_{t}^{\top}\right] \mathbb{E}\left[\mathbf{x}_{t} \mathbf{x}_{t}^{\top}\right]^{-1} \mathbb{E}\left[\rho_{t} \delta_{t} \mathbf{x}_{t}\right] \\
&=\mathbf{w}_{t}+\alpha \mathbb{E}\left[\rho_{t}\left(\mathbf{x}_{t}-\gamma \mathbf{x}_{t+1}\right) \mathbf{x}_{t}^{\top}\right] \mathbf{v}_{t} \\
&=\mathbf{w}_{t}+\alpha \rho_{t}\left(\mathbf{x}_{t}-\gamma \mathbf{x}_{t+1}\right) \mathbf{x}_{t}^{\top} \mathbf{v}_{t}
\end{aligned}
と更新する、\overline{PBE}のSGDの更新式が導出でき、GTD2と呼ばれる。(計算量O(d))
また、その改良版である、
\begin{aligned}
\mathbf{w}_{t+1} &=\mathbf{w}_{t}+\alpha \mathbb{E}\left[\rho_{t}\left(\mathbf{x}_{t}-\gamma \mathbf{x}_{t+1}\right) \mathbf{x}_{t}^{\top}\right] \mathbb{E}\left[\mathbf{x}_{t} \mathbf{x}_{t}^{\top}\right]^{-1} \mathbb{E}\left[\rho_{t} \delta_{t} \mathbf{x}_{t}\right] \\
&=\mathbf{w}_{t}+\alpha\left(\mathbb{E}\left[\rho_{t} \mathbf{x}_{t} \mathbf{x}_{t}^{\top}\right]-\gamma \mathbb{E}\left[\rho_{t} \mathbf{x}_{t+1} \mathbf{x}_{t}^{\top}\right]\right) \mathbb{E}\left[\mathbf{x}_{t} \mathbf{x}_{t}^{\top}\right]^{-1} \mathbb{E}\left[\rho_{t} \delta_{t} \mathbf{x}_{t}\right] \\
&=\mathbf{w}_{t}+\alpha\left(\mathbb{E}\left[\mathbf{x}_{t} \rho_{t} \delta_{t}\right]-\gamma \mathbb{E}\left[\rho_{t} \mathbf{x}_{t+1} \mathbf{x}_{t}^{\top}\right] \mathbb{E}\left[\mathbf{x}_{t} \mathbf{x}_{t}^{\top}\right]^{-1} \mathbb{E}\left[\rho_{t} \delta_{t} \mathbf{x}_{t}\right]\right) \\
&=\mathbf{w}_{t}+\alpha\left(\mathbb{E}\left[\mathbf{x}_{t} \rho_{t} \delta_{t}\right]-\gamma \mathbb{E}\left[\rho_{t} \mathbf{x}_{t+1} \mathbf{x}_{t}^{\top}\right] \mathbf{v}_{t}\right) \\
&=\mathbf{w}_{t}+\alpha \rho_{t}\left(\delta_{t} \mathbf{x}_{t}-\gamma \mathbf{x}_{t+1} \mathbf{x}_{t}^{\top} \mathbf{v}_{t}\right)
\end{aligned}
とするアルゴリズムがよく使われており、TDC(TD(0) with gradient corection)やGTD(0)と呼ばれる。
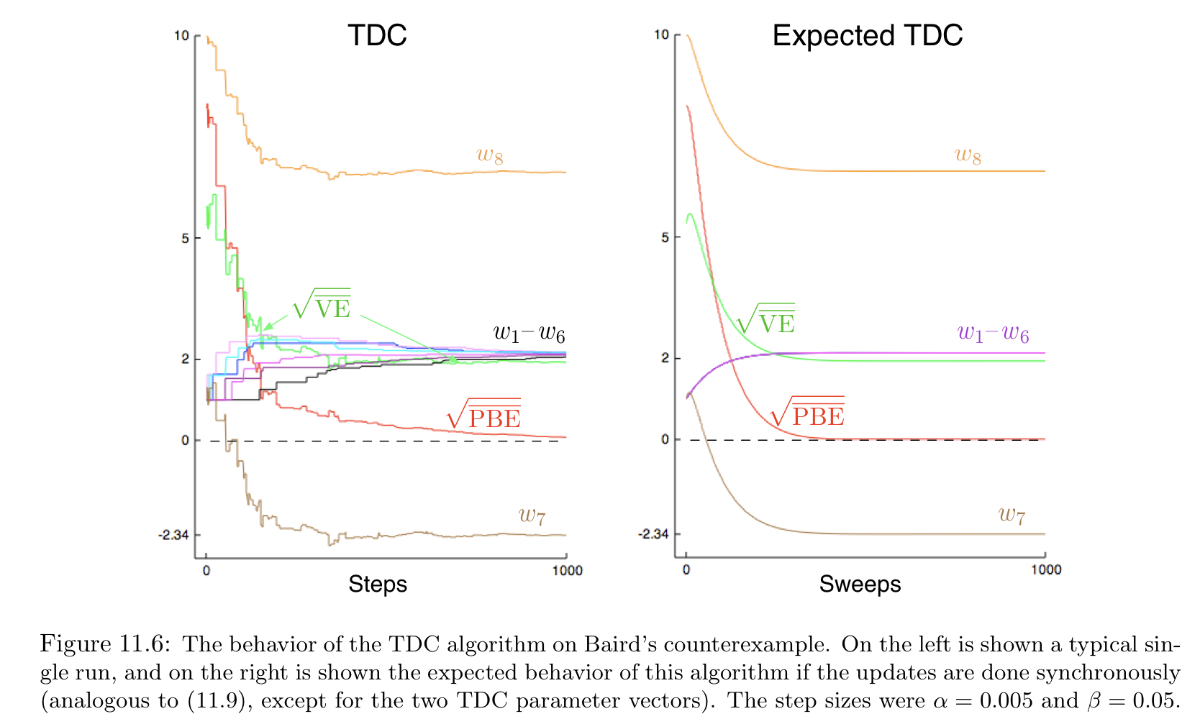
以下の図はベアードの反例を、
- 左:シングルで学習したときの学習曲線
- 右:並列に学習して期待値をとったときの学習曲線
である。\overline{PBE}によって正確な学習がなされていることが確認される。
GTD2やTDCは
と二つの学習があるが、2次学習の収束が十分早いと仮定される。
このような勾配TD法が安定的なオフポリシーの学習として広く使用され、
- GTD(λ)
- 非線形近似
- 勾配-半勾配のハイブリッド
などの拡張がなされている。
11.8 Emphatic-TD Methods
勾配法をオフポリシーに対応させる方法はもう一つ考えられている。
オフポリシーでは、行動ポリシーとターゲットポリシーの解離を埋めるために、

を用いて更新に重みづけを行ってきた。しかし、行動によって得られる状態分布とターゲットとなる状態分布は異なる場合がある。 e.g.)エピソードの始点が異なる場合
このように、ある特定の状態に興味があり、それがオンポリシー分布と異なる場合にさらにその分布に関して重みづけする方法が、9.10(#18)で紹介されたIntereset and Emphasisである。emphatic-TDの更新は以下のように、表される。
\begin{array}{l}
\delta_{t}=R_{t+1}+\gamma \hat{v}\left(S_{t+1}, \mathbf{w}_{t}\right)-\hat{v}\left(S_{t}, \mathbf{w}_{t}\right) \\
\mathbf{w}_{t+1}=\mathbf{w}_{t}+\alpha M_{t} \rho_{t} \delta_{t} \nabla \hat{v}\left(S_{t}, \mathbf{w}_{t}\right) \\
M_{t}=\gamma \rho_{t-1} M_{t-1}+I_{t}
\end{array}
ここで、I_tは興味度合いであり、割引率\gammaによって擬似的な終端を表現できる。
これによってあたかもI_tの分布で始点を選ぶように学習できる。
ベアードの反例も、emphatic-TD (I(s) = 1, \forall s)とすれば、\overline{VE}が下の図のように収束する。
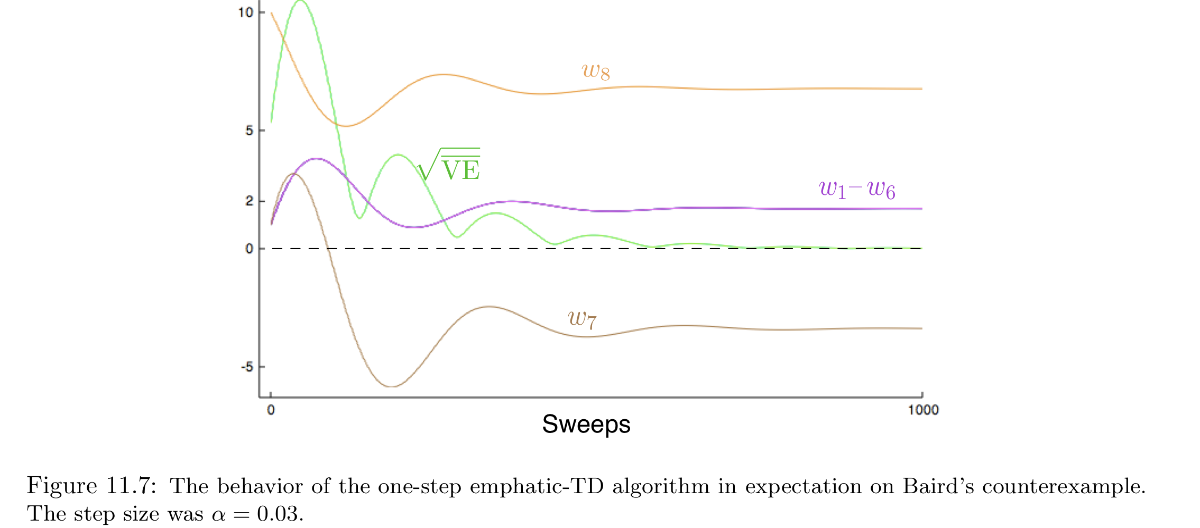
ただし、理論的には収束するものの、分散が高いため(実際振動している)、実験的に一貫した結果を得ることは不可能である。
11.9 Reducing Variance
- 行動ポリシーに似ているポリシーの中から最適なポリシーを選ぶことがオフポリシー学習の役割であるので、
- オフポリシーは一般にオンポリシーより分散が高い。
- ターゲットポリシーが直接得られていないので当然である。
- 数学的に言えば、ある状態について、b(A_t | S_t)が0に近いケースもあるから
-
b(A_t | S_t)が0に近いとSGDのステップサイズ(的な値)はかなり大きくなる
- これに対応するために、以下の方法が研究されている。
- モーメンタム (Derthick, 1984)
- 平均化 (Polyak, 1991; Ruppert, 1988; Polyak and Juditsky, 1992)
- ステップサイズの個別化 (Jacobs, 1988; Sutton, 1992)
- 関数近似における近似的な重要度サンプリング (Mahmood and Sutton, 2015)。
11.10 Summary
- オフポリシーは行動ポリシーとターゲットポリシーが異なる場合の学習
- テーブル形式オフポリシーはSarsaなどで自然な拡張ができた
- 関数近似ではブートストラップの半勾配法の不安定性という新たな課題があった。
- これに対応するために目的関数を再設計した。
- \overline{VE}
- \overline{BE}
- \overline{PBE}
-
\overline{PBE}であれば、2つのパラメータを同時に学習する方法によってO(d)で学習可能となった。
- 新しい手法であるEmphatic-TDはパラメータを増やさずに理論的に学習可能であるが、分散の大きさ壁となっている。
まとめ
Discussion