今日の概要
- 関数がテーブルではなくパラメータで圧縮した形式に.
- gradient method と semi-gradient method
- 線形関数による近似
Chapter 9 On-policy Prediction with Approximation
この章では強化学習における関数近似を紹介する.特に状態価値関数のオンポリシーを扱う.
-
ここまでの章:
- テーブル型の関数
- 任意のs \in S に対応した価値が実数値として与えられる設定
-
この章:
- パラメータ \mathbf{w} を用いて状態価値関数を近似
-
\hat{v}(s, \mathbf{w}) \approx v_{\pi}(s)と表記する
-
\hat{v}が
- 線形関数なら\mathbf{w}は特徴量に対する重みベクトル
- 多層ニューラルネットなら重み\mathbf{w}は(connection weight)など
- 決定木ならば\mathbf{w}は全ての分割点と葉の重みなど
多くの場合,この\mathbf{w}の次元は状態の数よりも小さく設定される.
ここで注目すべきはある状態について価値が更新されたとき,それに関連して他の状態の価値も更新される点である.これをgeneralization と言う.
関数近似(generalization)のメリットは,
- メモリ削減
- 関係する状態の結果から類推して学習できる
- 状態を部分的にしか観測していなくても未観測な状態について学習できる
といった点があげられる.一方で運用やアルゴリズム/結果の理解を難しくさせていると言うデメリットもある.
9.1 Value-function Approximation
価値関数の近似について述べていく.
この本で紹介されている強化学習の手法は,価値関数の推定を繰り返して更新していく方法である.
復習
\begin{aligned}
v_{\pi}(s)&=\mathbb{E}_{\pi}[R_t + \gamma R_{t+1} + \gamma^2 R_{t+2} + \cdots | \ S_t = s]\\
&=\mathbb{E}_{\pi}[G_t\ | \ S_t = s] \\
&=\mathbb{E}_{\pi}[R_{t+1} +\gamma G_{t+1} \ |\ S_t = s]\\
&=\mathbb{E}_{\pi}[R_{t+1} +\gamma v_{\pi}(S_{t+1})\ | \ S_t = s]\\
&=\mathbb{E}_{\pi}[\sum_{k=t}^{t+n} R_{k} \gamma^{k-t-1} + \gamma^{n} v_{\pi}(S_{t+n})\ | \ S_t = s]
\end{aligned}
- モンテカルロ:エピソードの終端までの情報をターゲット (数式2行目)
- TD(0):次の状態の推定価値が正しいと仮定したターゲット(数式4行目)
- n-step TD:2つの中間をとった形式 (数式5行目)
ここからはその更新対象とそのターゲットの関係を表す記号として \mapsto を導入する.
これを用いて,関数近似の場合の上記3つを記述すると,
- MC:S_t \mapsto G_t ~~~ (= R_t + \gamma R_{t+1} + \cdots)
- TD(0):S_t \mapsto R_{t+1} + \gamma \hat{v}(S_{t+1}, \mathbf{w_t})
- n-step TD:S_t \mapsto G_{t:t+n} (= R_t + \gamma R_{t+1} + \cdots + \gamma^{n}R_{t+n} + \hat{v}(S_{t+n}, \mathbf{w_t}))
となる.また,DPの政策評価における更新は,
- DP 政策評価:s \mapsto \mathbb{E}_{\pi}[R_{t+1} + \gamma \hat{v}(S_{t+1}, \mathbf{w_t})|S_t = s]
と書ける.(任意の状態sについて全て更新すると言う意味)
s \mapsto uの学習は入力値-出力値がより正しくなるような関数を見つける作業だと言うことができ,各更新はsの推定価値をuの近似としてより尤もらしい値に近づけている.ただし,以下の点に注意する.
- ここまで:ある状態sの価値を更新してその他の状態は動かさない
- ここから:1つの状態価値について更新すると他の状態の価値も更新される
入力と出力の例を用いて入出力を関係付ける関数を近似的に求める機械学習は教師あり学習と言う.そして出力が実数のときは特に関数近似法(function approximation)と呼ばれる(?).このようにして各更新を単純な教師あり学習としてみることで強化学習を行うことができる.基本的に,
などどんな手法でも可能であるが,全てが強化学習にふさわしいわけではない.それはオンライン性の面で,
- インクリメンタルに取得したデータから効率的に学習できる
- 非定常な(時間経過によって変化する)目的関数を扱える
ことが求められる.これは同じ訓練データでも異なる値をとることが多いためである.また,中には政策\piを変化させながら行動価値q_{\pi}を学習する方法(GPI, Generalized Policy Iteration)も存在する.
9.2 The Prediction Objective (\overline{VE})
予測の目的関数\overline{VE}について説明する.
テーブル形式の関数では,
- 真の分布から観測される実現値から推定
- それぞれの状態が独立
しているため予測の精度についてあまり重要視しなかった.しかし,関数近似をする際は,
- ある状態の更新が他の多くの状態に影響を与える
- 全ての状態の値を得ることができない
と言う性質がある.そのため\mu(s) \geq 0, \sum_s \mu(s) =1となるように重み\muを決めて各状態について誤差を重視する度合いを決める必要がある.そしてその\muを用いて最小化すべき目的関数(Mean Squared Value Error)
\overline{VE} = \sum_{s \in S} \mu(s) [v_{\pi}(s) - \hat{v}(s, \mathbf{w})]^2
を設定する.この\muは状態sを通る頻度などで設定される.On-policyの学習の時,この\muはオンポリシー分布(On-policy distirbution)と呼ぶ.(この章ではこれを主に用いる)
でそれぞれ区別する必要があるが,継続的なタスクではいずれ定常な分布となる.また,エピソードのタスクでは以下のように\muは計算される.
-
h(s):sでエピソードが始まる確率
-
\eta(s):s推移する平均的な回数
とすると,
\eta(s) = h(s) + \sum_{\bar{s}}\eta(\bar{s}) \sum_a \pi(a|\bar{s})p(s | \bar{s},a), ~~ (\forall s \in S)
となる.そして,割引率のないオンポリシー分布は,
\mu(s) = \frac{\eta(s)}{\sum_s \eta(s)}
と計算できる.(割引率が\gammaを導入したい場合\etaの式の第2項にかける)
理想的には\overline{VE}(\mathbf{w}^{*}) \leq \overline{VE}(\mathbf{w}), \forall \mathbf{w}なる大域的最適解\mathbf{w}^{*}を見つけたいが,これは難しいことも多いため局所解を見つけることが目標となる.とはいえ,収束する保証はなく,発散する可能性もある.
続く二つのセクションでは,
- 現状の推定値を用いて次の時点の推定値の更新を行う関数近似の強化学習のフレームワーク
- (特に線形関数を用いた)勾配計算に基づく更新方法
について説明する.
9.3Stochastic-gradient and Semi-gradient Methods
確率的勾配降下法(SGD)をベースとした強化学習の手法を紹介する.
gradient method
まず,
- \mathbf{w} = (w_1, w_2, \ldots, w_d)^T
-
\hat{v}(s,\mathbf{w})は任意のs \in Sについて\mathbf{w}で微分可能
- タイムステップtごとに\mathbf{w}を更新
-
tにおける\mathbf{w}を\mathbf{w}_tとする
- 各タイムステップにおいて,S_t \mapsto v_{\pi}(S_t)のサンプルを観測
と設定する.このとき,
と言えるため,\overline{VE}を最小化する確率的勾配降下法は,
\begin{aligned}
\mathbf{w}_{t+1} &= \mathbf{w}_t - \frac{1}{2}\alpha \nabla \mathbb{E}_{\mu}[\overline{VE}(\mathbf{w}_t)]\\
&\approx \mathbf{w}_t - \frac{1}{2}\alpha \nabla \left[v_{\pi}(S_t) - \hat{v}_{\pi}(S_t,\mathbf{w}_t ) \right]^2\\
&= \mathbf{w}_t + \alpha\left[v_{\pi}(S_t) - \hat{v}_{\pi}(S_t,\mathbf{w}_t ) \right]\nabla\hat{v}_{\pi}(S_t,\mathbf{w}_t )
\end{aligned}
のような更新式で表される.
(勾配を降るようにパラメータを更新する勾配法を確率的なサンプリングによって行う)
ただし,
\nabla f(\mathbf{w}) = \left( \frac{\partial f(\mathbf{w})}{\partial w_1}, \frac{\partial f(\mathbf{w})}{\partial w_2},\ldots, \frac{\partial f(\mathbf{w})}{\partial w_d} \right)^T
である.しかし,真のv_{\pi}は観測できない.これを前節までと同様に,観測したデータからターゲットを推定した値U_tで代用(S_t \mapsto U_t)し,
\mathbf{w}_t + \alpha\left[U_t - \hat{v}_{\pi}(S_t,\mathbf{w}_t ) \right]\nabla\hat{v}_{\pi}(S_t,\mathbf{w}_t )
とする.もちろんU_tにはノイズが含まれているが,U_tが不偏推定量すなわち
\mathbb{E}_{p, \pi} [U_t | S_t = s] = v_{\pi}(S_t)
であれば,十分小さい\alphaのもと\mathbf{w}_tは局所最適解に収束することが保証される.((2.7)と同様.)
例えば,政策\piによって実際(もしくはシミュレーション)の相互作用から生成される観測値があるとすると,真の分布から生成される報酬の期待値が真の価値であるから,モンテカルロ法ではU_t = G_tとすれば不偏である.疑似コードは以下のようになる.

semi-gradient method
既知の推定値を正しいとした元で次の時点の推定を行うブートストラップな手法(DP, TDなど)では,これが難しい.例えばDPでは
\sum_{a,s',r}\pi(a|S_t)p(s',r|S_t,a)[r + \gamma\hat{v}(s',\mathbf{w}_t)]
としてしまい,\mathbf{w}_tに依存してしまうためバイアスが生まれる.このことからもわかるように,収束させるにはターゲットを\mathbf{w}_tについて独立にする必要がある.
ターゲットが\mathbf{w}_tに依存する場合をsemi-gradient法(半勾配法?)と呼ぶ.
この方法は勾配法(gradient method)と違い,ロバストに収束することが一般に保証されていない.
しかし,semi-gradient methodには以下のメリットがあり,利用される場合がある.
-
\hat{v}が線形関数のときは収束する.
- 高速な学習が可能
- 継続的にオンラインで学習可能
例えば,典型的なsemi-gradient法のsemi-gradient TD(0)はターゲットU_tを
U_t = R_{t+1} + \gamma \hat{v}(S_{t+1},\mathbf{w})
として行う.疑似コードは以下のように表される.

state aggregation (状態集約)
状態集約は最も簡単な関数近似で状態をグループ化し,各グループに一つの価値をもつ.
これはSGDの特殊な形式だと考えることができ,
-
\mathbf{w}:各グループの価値を合わすグループ数次元のベクトル
- 勾配\nabla\hat{v}のg番目の要素は,
\frac{\partial \hat{v}(S_t, \mathbf{w})}{\partial w_g} = \begin{cases}
1 & (S_tがg番目のグループに属する) \\
0 & (その他)
\end{cases}
として考えられる.
Example 9.1 State Aggregation on the 1000-state Random Walk
Example 6.2などで行ったランダムウォークについて1000個の状態がある場合を考える.
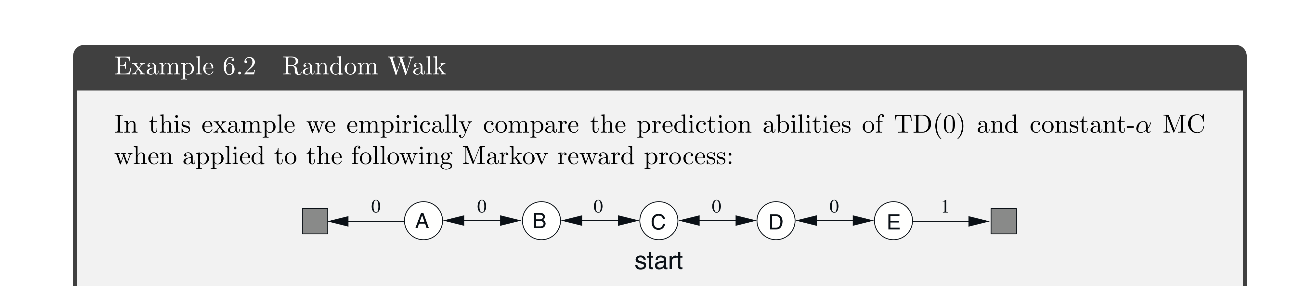
- 左から右に番号1~1000の状態
- 500からスタート
- 今いる状態から左の100個もしくは右の100個の合計200状態に当確率で遷移
- はみ出したとき,もしくは1,1000に到達した時点で終了
- 左で終了すると報酬-1
- 右で終了すると報酬+1
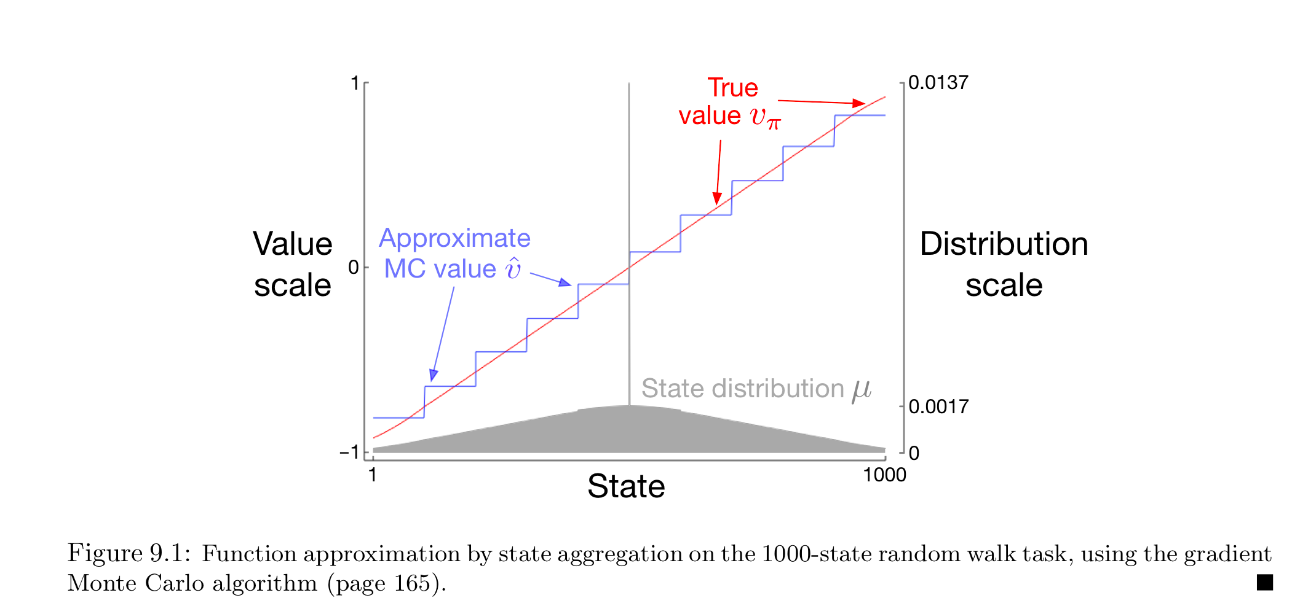
- 赤線は真の価値関数
- 灰色は分布\mu
- 青線は以下の条件でgradient MCを行った際の各グループの価値
- 100000エピソード
- \alpha = 2 \times 10^{-5}
- 左から100個ずつ10グループに集約
この結果から
- おおよそ\overline{VE}の大域的最適解
- 分布の重み付けによって端の方は誤差が多少大きくなっている
と言うことがわかる.
Linear Method
\hat{v}(s, \mathbf{w})が線形の場合の(semi)勾配法について説明する.
gradient linear method
- x_i : \mathcal{S} \rightarrow \mathbb{R} ~~ (i = 1, 2, \ldots, d)
- 状態sの特徴量:\mathbf{x}(s) = (x_1(s), x_2(s), \ldots, x_d(s))^T
- \hat{v}(s, \mathbf{w}) = \mathbf{w}^T \mathbf{x}(s) = \sum_{i=1}^d w_i x_i(s)
とする.このとき,
\nabla \hat{v}(s, \mathbf{w}) = \mathbf{x}(s)
となるから,一般的なSGDにおける更新は,
\mathbf{w}_{t+1} = \mathbf{w}_t + \alpha \left[U_t - \hat{v}(S_t, \mathbf{w}_t)\right]\mathbf{x}(S_t)
数学的に扱いやすいため解析によく用いられる.収束などの結果はこの線形関数に関してであることが多い.
特に線形の場合,局所最適解がただ一つであることから,局所最適解に収束する保証があるアルゴリズムが大域的最適解に収束することが保証されることになる.(e.g. gradient MC)
semi-gradient linear method
semi-gradient TD(0)も線形関数による近似であれば収束することが知られている.
(ただし,gradient methodと違い,大域的最適解への保証ではない)
更新式は,\mathbf{x}_t = \mathbf{x}(S_t)として,
\begin{aligned}
\mathbf{w}_{t+1} &= \mathbf{w}_t + \alpha \left(R_{t+1} + \gamma\mathbf{w}_t^T \mathbf{x}_{t+1}- \mathbf{w}_t^T \mathbf{x}_{t}\right)\mathbf{x}_t\\
&= \mathbf{w}_t + \alpha \left(R_{t+1}\mathbf{x}_t - \mathbf{x}_t\left(\mathbf{x}_t - \gamma \mathbf{x}_{t+1}\right)^T \mathbf{w}_t\right)
\end{aligned}
となる.ここで,
\mathbf{b} = \mathbb{E}_{\mu,\pi,p}\left[R_{t+1}\mathbf{x}_{t}\right] , ~~ A =\mathbb{E}_{\mu,\pi,p}\left[\mathbf{x}_{t}\left(\mathbf{x}_{t} - \gamma\mathbf{x}_{t+1} \right)^T\right]
とすると,\mathbf{w}_{t}が与えられたときの平均的な\mathbf{w}_{t+1}は,
\mathbb{E}_{\mu,\pi,p}\left[\mathbf{w}_{t+1} | \mathbf{w}_{t}\right] = \mathbf{w}_t + \alpha\left(\mathbf{b} - A\mathbf{w}_t\right) ~~~~ \cdots (*)
と計算でき,\mathbf{b} - A\mathbf{w}_{TD} = \mathbf{0}なる重みベクトル\mathbf{w}_{TD}に至ったとき更新が停止する.この\mathbf{w}_{TD}は,TD不動点(TD fixed point)と呼ばれ,
\mathbf{w}_{TD} = A^{-1}\mathbf{b}
と計算できる.実際,semi-gradient TD(0)ではこの点に収束することがわかっている.
収束の証明と逆行列の存在を以下で証明する.
[証明] \mathbf{w}_{TD}への収束
以下を仮定して進める(あとで証明).
上の式(*)を変形すると,
\mathbb{E}[\mathbf{w}_{t+1} | \mathbf{w}_{t}] = (I - \alpha A)\mathbf{w}_{t} + \alpha \mathbf{b}
と表せる.マルコフ過程であるから,
\mathbb{E}[\mathbf{w}_{t+1} | \mathbf{w}_{t-1}] = (I - \alpha A)\mathbb{E}[\mathbf{w}_{t} | \mathbf{w}_{t-1}] + \alpha \mathbf{b}
と表せて,漸化式を解くと,
\mathbb{E}[\mathbf{w}_{t+1} | \mathbf{w}_{1}] = (I - \alpha A)^t (\mathbf{w}_{1} - \mathbf{c}) + \mathbf{c}, ~~ \mathbf{c} = A^{-1}\mathbf{b}
となる.\alphaは十分に小さく,Aが正定値より対角要素が全て正であるから,
\lim_{t \to \infty} \mathbb{E}[\mathbf{w}_{t+1} | \mathbf{w}_{1}] = \mathbf{c} = \mathbf{w}_{TD}
より\mathbf{w}_{TD}への収束が示される.
証明終了
[証明] Aが正定値
継続的なタスクで\gamma < 1のとき,linear TD(0)での行列Aは以下のように表せる.
\begin{aligned} \mathbf{A} &=\sum_{s} \mu(s) \sum_{a} \pi(a \mid s) \sum_{r, s^{\prime}} p\left(r, s^{\prime} \mid s, a\right) \mathbf{x}(s)\left(\mathbf{x}(s)-\gamma \mathbf{x}\left(s^{\prime}\right)\right)^{\top} \\ &=\sum_{s} \mu(s) \sum_{s^{\prime}} p\left(s^{\prime} \mid s\right) \mathbf{x}(s)\left(\mathbf{x}(s)-\gamma \mathbf{x}\left(s^{\prime}\right)\right)^{\top} \\ &=\sum_{s} \mu(s) \mathbf{x}(s)\left(\mathbf{x}(s)-\gamma \sum_{s^{\prime}} p\left(s^{\prime} \mid s\right) \mathbf{x}\left(s^{\prime}\right)\right)^{\top} \\ &=\mathbf{X}^{\top} \mathbf{D}(\mathbf{I}-\gamma \mathbf{P}) \mathbf{X} \end{aligned}
ただし,
-
X \in \mathbb{R}^{|\mathcal{S}|\times d}:特徴行列
-
P \in \mathbb{R}^{|\mathcal{S}|\times \mathcal{S}}:推移確率行列
-
D \in \mathbb{R}^{|\mathcal{S}|\times \mathcal{S}}:diag(\mu)
を表す.
ここで,以下の既知の2つの定理を証明なしに用いる.
定理1
正方行列Mについて,対称行列SがS = M + M^Tと表されるとき,Sが正定値であることとM正定値であることは必要十分条件である.
定理2
対称行列Sについて,全ての対角要素が正でかつ,対応する対角外要素の(絶対値?)の和よりも大きいとき,対称行列Sは正定値行列である.
以上を用いれば以下の手順で証明できる.
-
D(I - \gamma P)の対角要素が正でそのほかが負
-
D(I - \gamma P)の行の和が正
-
D(I - \gamma P)の列の和が正
-
D(I - \gamma P)が正定値
- Aが正定値
1. D(I - \gamma P)の対角要素が正でそのほかが負
Dが対角行列,Pの要素が確率(0以上1以下),\gamma < 1より自明.
2. D(I - \gamma P)の行の和が正
Pが遷移確率行列で,行の和をとると1であるため自明
3. D(I - \gamma P)の列の和が正
\begin{aligned} \mathbf{1}^{\top} \mathbf{D}(\mathbf{I}-\gamma \mathbf{P}) &=\boldsymbol{\mu}^{\top}(\mathbf{I}-\gamma \mathbf{P}) \\ &=\boldsymbol{\mu}^{\top}-\gamma \boldsymbol{\mu}^{\top} \mathbf{P} \\ &=\boldsymbol{\mu}^{\top}-\gamma \boldsymbol{\mu}^{\top} \\ &=(1-\gamma) \boldsymbol{\mu} \end{aligned}
4. D(I - \gamma P)が正定値
S = D(I-\gamma P) + D(I - \gamma P)^Tの対角要素と対角以外の要素について考えると,上記1,2,3より,全ての対角要素が正でかつ対応する対角外要素の絶対値の和よりも大きい.よって,定理2よりSは正定値である.また,これにより定理1よりD(I-\gamma P)が正定値である.
概念図:
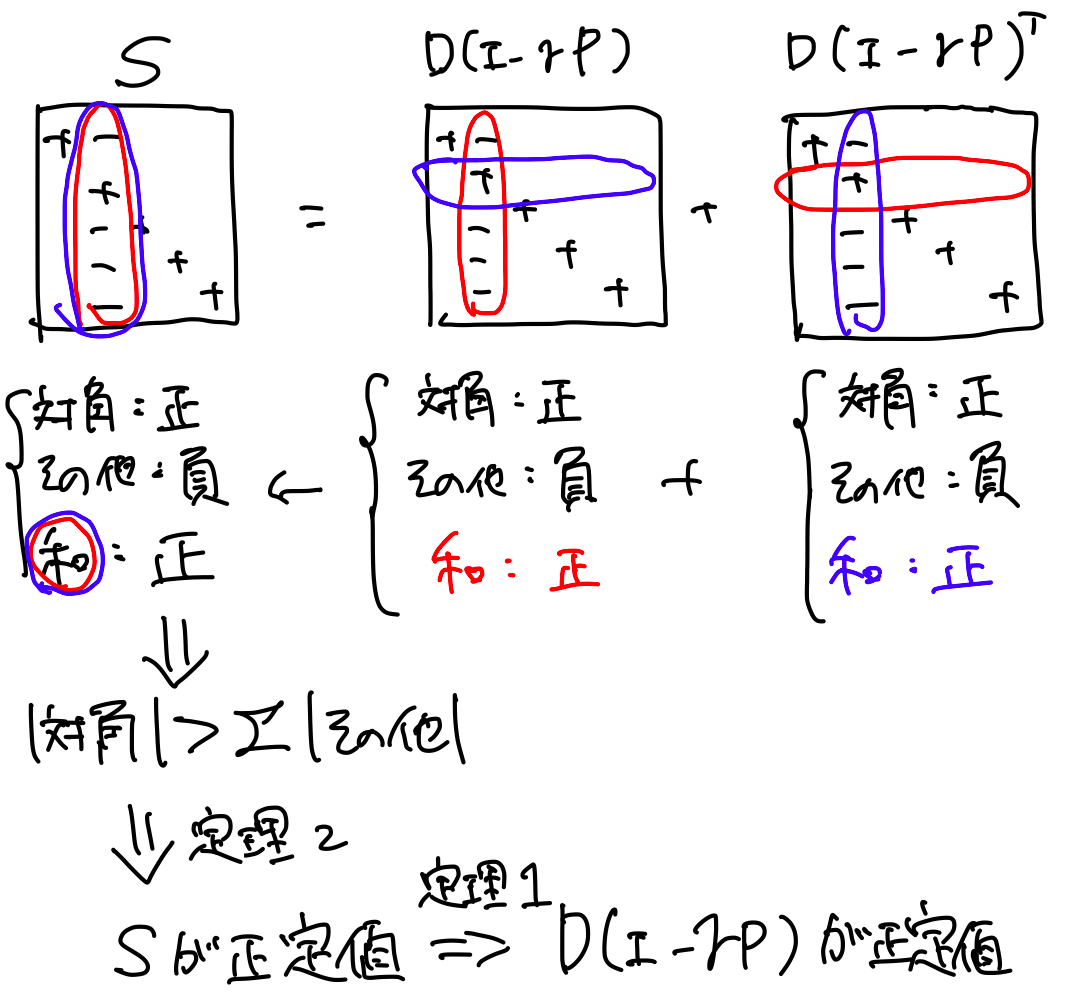
5. Aが正定値
任意の\mathbf{y} \in \mathbb{R}^{|S|}について,\mathbf{z} = X\mathbf{y}とすると,
\begin{aligned}
\mathbf{y}^T A \mathbf{y} &= \mathbf{y} X^T D(I-\gamma P) X \mathbf{y}\\
&= (X \mathbf{y})^T D(I-\gamma P) X \mathbf{y}\\
&= \mathbf{z}^T D(I-\gamma P) \mathbf{z} > 0
\end{aligned}
より Aは正定値である.
証明終了
解の性能について
収束する解\mathbf{w}_{TD}は,
\overline{VE}(\mathbf{w}_{TD}) \leq \frac{1}{1-\gamma} \min_{\mathbf{w}} \overline{VE}(\mathbf{w})
を満たすことが示される.つまり,最低でも大域的最適解の\frac{1}{1-\gamma}倍の性能が保証されている.しかし,\gammaは1に近いことが多いため,TD(0)では性能が低下する可能性もある.
6,7章でも紹介された通り,MCに比べて分散が小さいことや高速であるため,どの手法が最適化は問題の性質や許容できる学習時間に依る.
また,On-policy 分布にしたがって更新されることは重要なポイントであり,そうでない場合は発散する可能性がある.このような状況での可能な開放については11章で扱う.
n-step semi-gradient TD
semi-gradient TD(0)と同様に,n-stepでもsemi-gradient methodが考えられる.
\mathbf{w}_{t+n} = \mathbf{w}_{t+n-1} + \alpha\left[G_{t:t+n} - \hat{v}_{\pi}(S_t,\mathbf{w}_{t+n-1}) \right]\nabla\hat{v}_{\pi}(S_t,\mathbf{w}_{t+n-1} )
ただし,
G_{t:t+n} \doteq R_{t+1}+\gamma R_{t+2}+\cdots+\gamma^{n-1} R_{t+n}+\gamma^{n} \hat{v}\left(S_{t+n}, \mathbf{w}_{t+n-1}\right), \quad 0 \leq t \leq T-n

その他のブートストラップ手法でのsemi-gradinet method
- semi-gradient DP
- semi-gradient Sarsa(0)
でも同様に収束することが示される.また,エピソードのタスクでも学習率の減衰など多少の条件を付け加えれば良い.
Example 9.2 Bootstrapping on the 1000-state Random Walk
semi-gradient method を用いた状態集約の学習を示す.
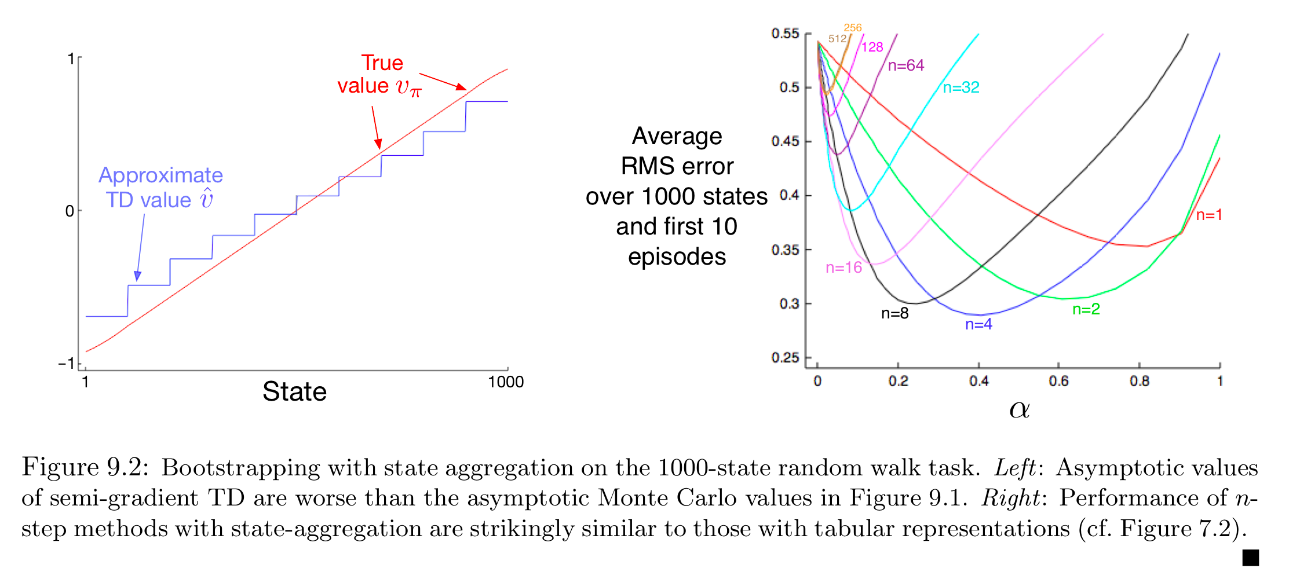
- 左の図はsemi-gradient methodのTD法による推定値
- 右の図はTDのステップ数と学習率の違いによる誤差の変化
を表す図で,左の図からは多少の誤差が生じていることがわかる.しかし右図から,10エピソードでの学習結果として7章のテーブル型のn-step TDと同じような結果が得られることがわかり,学習の速さなどの面でメリットがあることがわかる.
今日のまとめ
- テーブル関数を圧縮して関数近似
- 関数近似では一つの更新があらゆる状態の価値の更新になる
- ターゲットが不偏推定量のとき(e.g. MC法)はgradient method
- 不偏推定量でないとき(e.g. TD法)はsemi-gradient method
- 線形関数による近似であれば多くのsemi-gradient methodで局所解に収束
Discussion