線形代数から共変・反変を完全に理解したい（エンジニア基準）

概要

共変・反変について，「完全に理解した」と言えるまで見ていく記事です．
エンジニア基準の「完全に理解した」
それはすなわち，ここで言うところの「共変・反変なんも分らん」の前段階まで進みます．

共変・反変の例

鼻☆塩☆塩
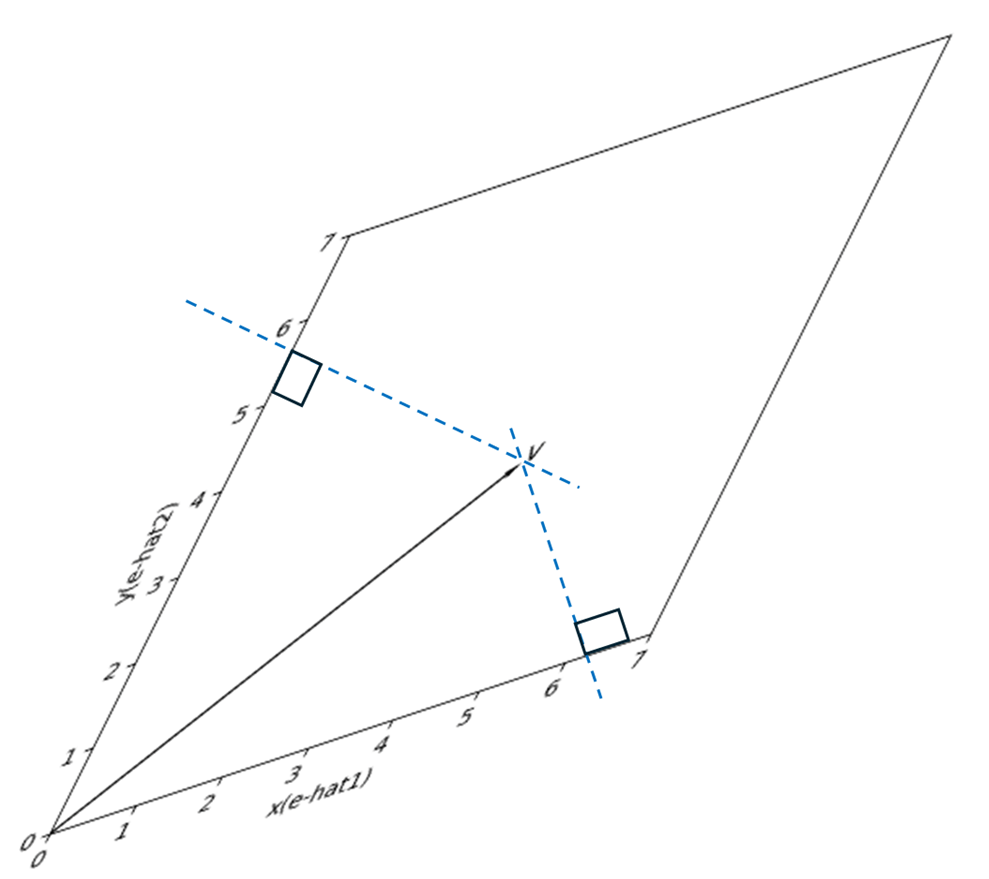
皆さんは下のようなベクトルを読むとき，どのように読んでいるだろうか．

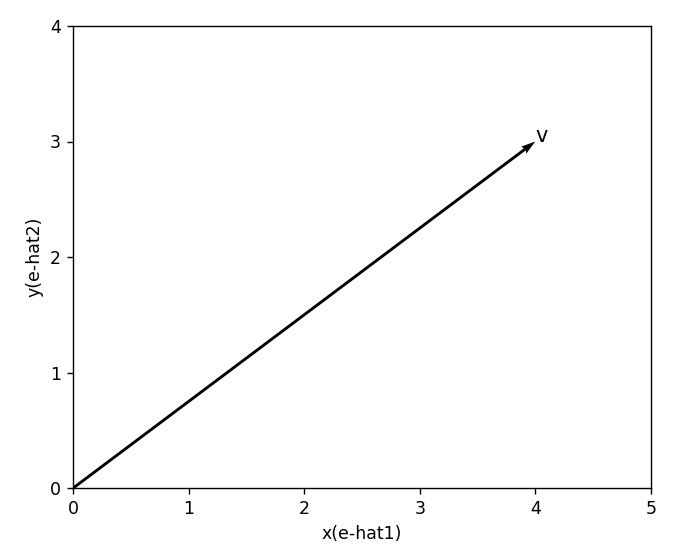
正解は $v=(4,3)Tv=(4,3)^T$ なのだが，頭の中では，

1. 垂直な線を引いて，その目盛りを読んでいる（内積）
2. 基底ベクトルが何倍されて足されているか（線形結合）

などのように考えているだろう（強制）
視覚的にみると，1の方法は

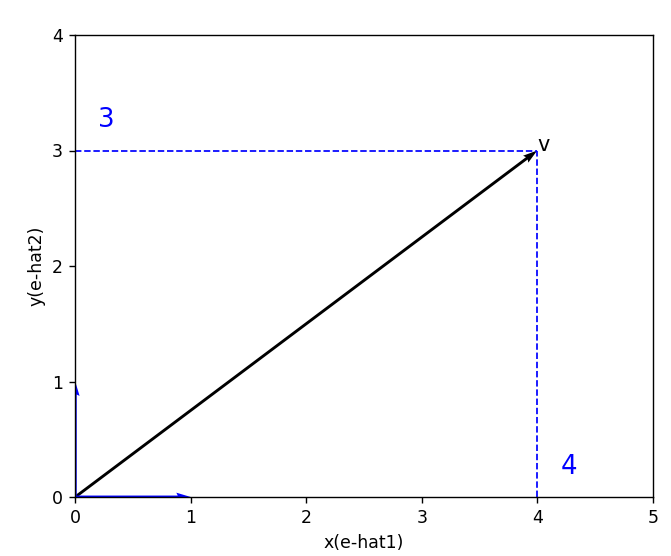
対して2の方法は

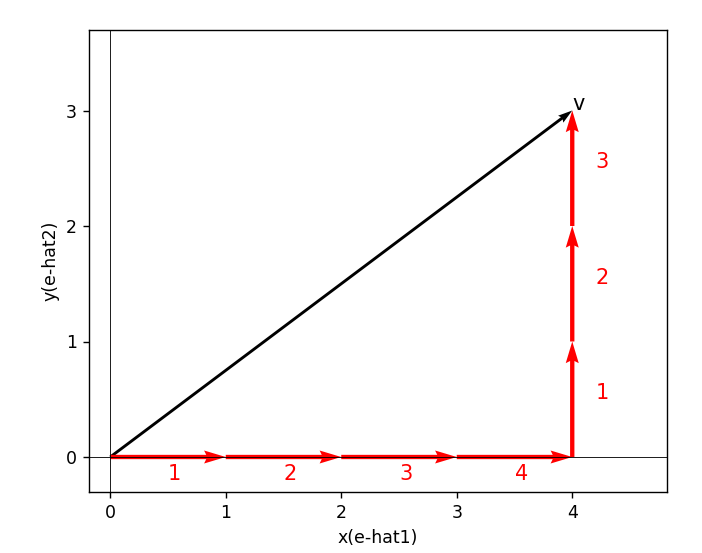
のように考えているはずである．

何を当たり前のことを！しかも両者同じことではないか！と感じるのではないだろうか．ワイトもそう思います．

いきなりで申し訳ないが，これが共変・反変である．
しかし，見た目一緒だしこのような区別は必要ないのでは？と思うだろう．
実際1984年にシュッツという方が

共変と反変が見捨てられた理由は，それらが非常に異なったものを混同させるからである．(ダニエル・フライシュ, 物理のためのベクトルとテンソル, p.118)

と言っており，当時も似たようなものと誤解されて見捨てられたことがあったらしい．ムズそう（小並感）

---

そこで，直感的な実用例を考えてみようと思う．
私はメガネをかけている．したがって，私から見れば，基底は少し歪んでいるだろう．
他にも極端な例を挙げれば，半魚人の次郎君は魚眼レンズにより基底は歪んで見えるだろう．
そういう状況を仮定してみる．

さて，私と次郎君が先ほどの図を見ると，

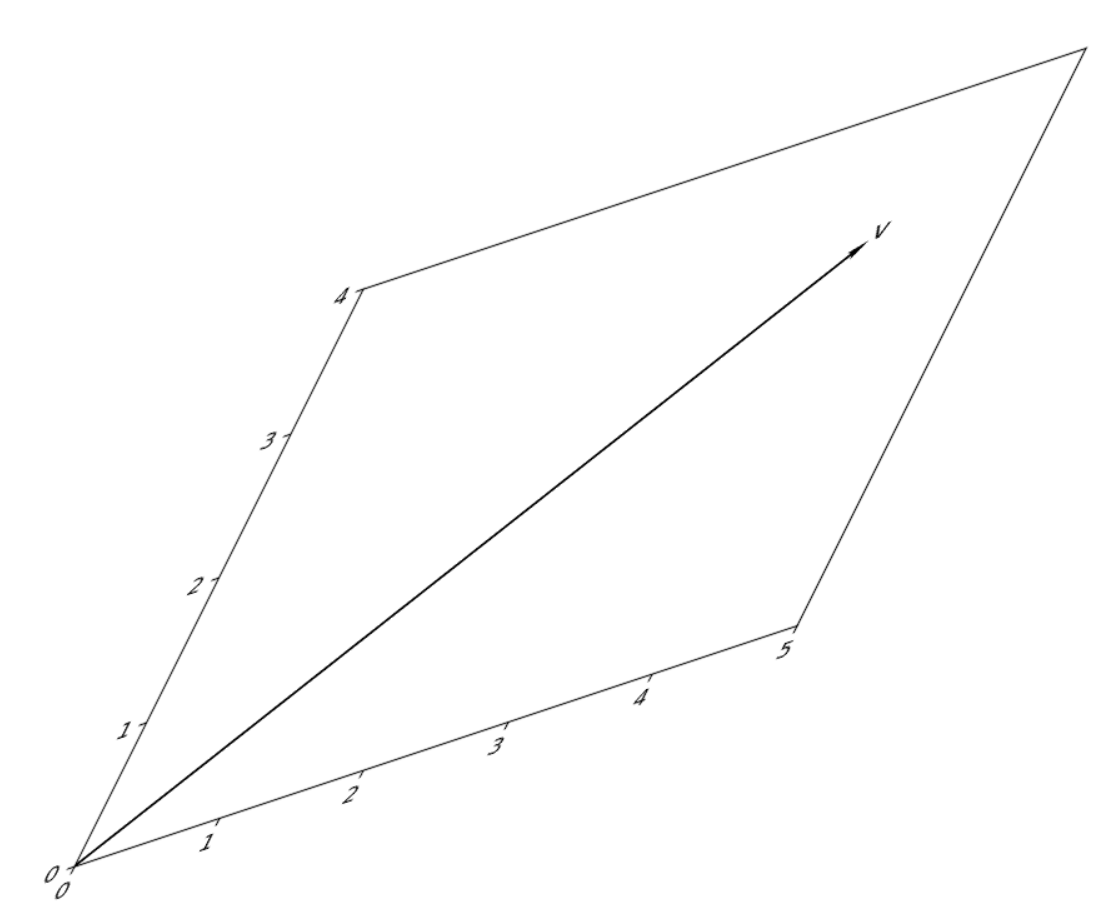
このように見えたようだ．私のことを魚人呼ばわりするのはやめていただきたい．

ここで，1の方法で見てみよう．すると

となるが，線形結合をしてみると

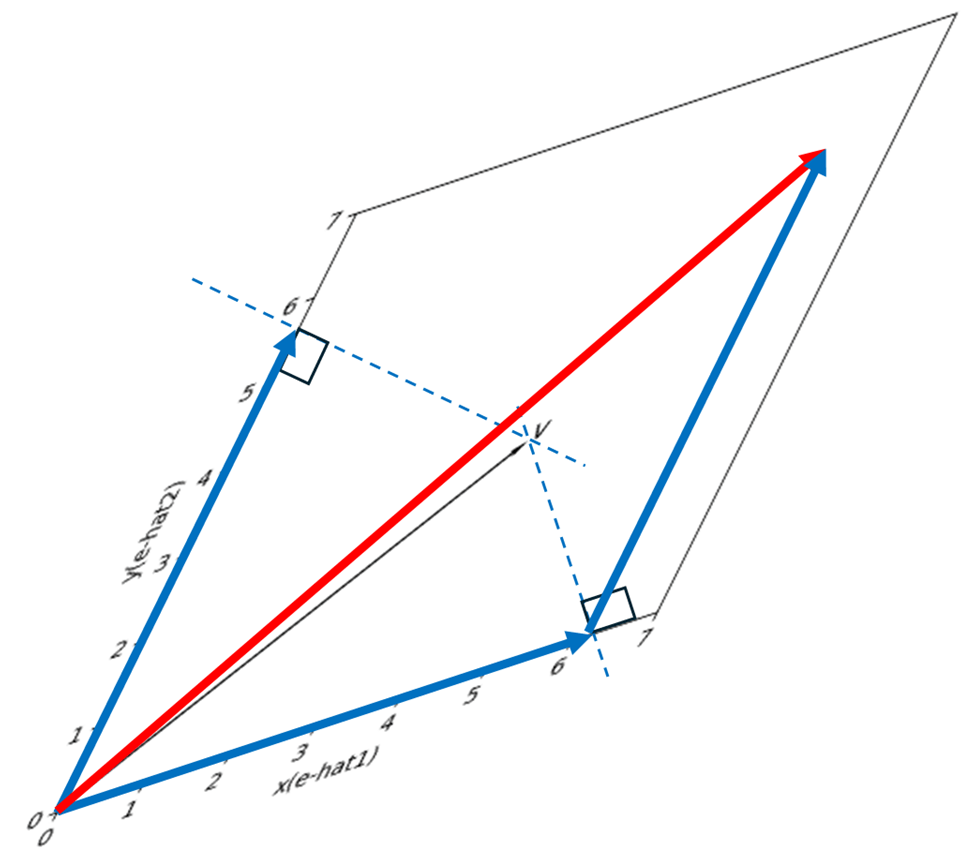
となり，元のベクトルを復元できなかった．魚人はとても悲しんだ．

何がいけなかったのか．

メガネ筆者から見た座標系（黒線）で，
メガネを外した視点で見た垂直な線(青点線)
を引いて考えてしまったからである．
実際，メガネをかけたまま垂直な線を引いてみれば，その垂直な線までもがメガネで歪み，このようになっただろう．

これなら上手く線形結合できる．

このように，ベクトルの和（線形結合）が正しく機能する/しない目盛りの読み方が存在することが分かった．

まとめると，共変・反変は座標が直交していない座標系で出現する．
極座標とかが良い例である．

---

この目盛りの数値を成分
読む手掛かりとするベクトルを基底ベクトル
と呼び，
垂直な線を使うかどうかで，共変成分・反変成分・共変基底・反変基底のセットが存在する．
というかそう名付けられているようだ．

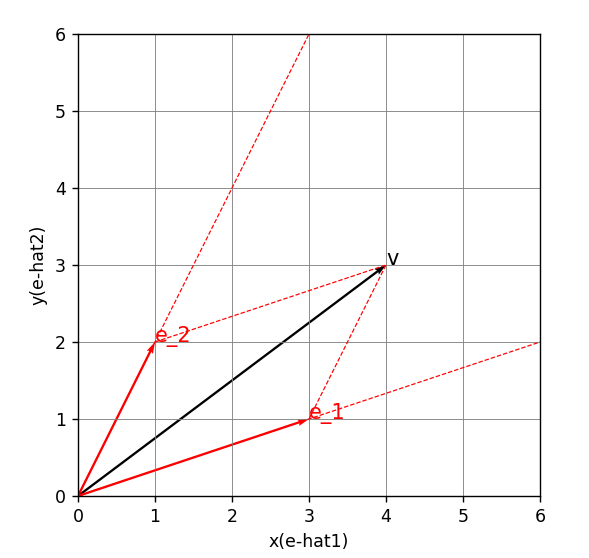
言い換えると，一つのベクトル

$$v=(43)v=\begin{pmatrix} 4 \\ 3 \end{pmatrix}$$

に対する読み方は

1. 標準基底に垂直＝平行な線（黒線）を引いて得る標準成分$(4,3)(4,3)$と標準基底$e^i\bm{\hat e_i}$の読み方

$$=4(10)+3(01)=4e^1+3e^2 = 4\begin{pmatrix} 1 \\ 0 \end{pmatrix}+3\begin{pmatrix} 0 \\ 1 \end{pmatrix}=4\bm{\hat e_1}+3\bm{\hat e_2}$$

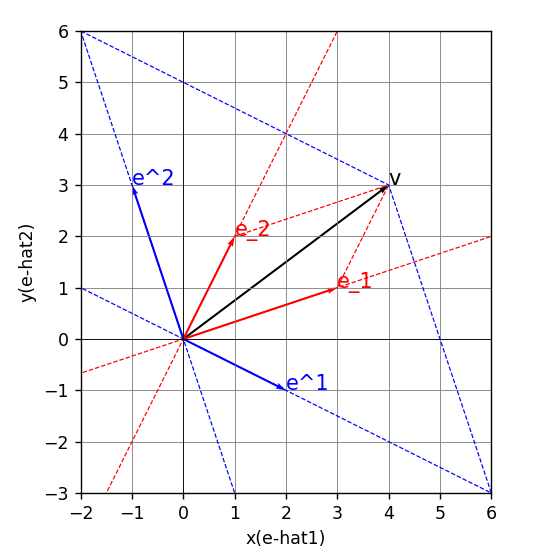
2. 共変基底に垂直な線（青点線）を引いて得る共変成分$(3,2)(3,2)$と反変基底$ei\bm e^i$の読み方

$$=3(2−1)+2(−13)=3e1+2e2 = 3\begin{pmatrix} 2 \\ -1 \end{pmatrix}+2\begin{pmatrix} -1 \\ 3 \end{pmatrix}=3\bm{e^1}+2\bm{e^2}$$

3. 共変基底に平行な線（赤点線）を引いて得る反変成分$(1,1)(1,1)$と共変基底$ei\bm e_i$の読み方

$$=1(31)+1(12)=1e1+1e2 = 1\begin{pmatrix} 3 \\ 1 \end{pmatrix}+1\begin{pmatrix} 1 \\ 2 \end{pmatrix}=1\bm{e_1}+1\bm{e_2}$$

の３通り存在するといえる．

なお，標準成分・標準基底は，筆者が分かりやすいよう導入した造語であるので注意されたい．
名前つけてくれれば当時の私でも区別できたのに！
魚人ピチピチで草

閑話休題．
ここからは視覚的にではなく，線形代数を使って厳密に定義・導出してみる．

線形代数・定義

定義

この辺の定義は正直読み飛ばしてよい．数学書によくある，正確性のためにとりあえず定義連ねるぞフェーズである．詳しくはヨビノリ先生の動画などを参照されたい．

この記事では，
始域Xから終域Yへの写像fを$f:X→Yf:X\to Y$と表現し，
「その元xをf(x)に写す．写し方はyと定義する」を$x↦f(x):=yx\mapsto f(x):=y$と書く．

ベクトル空間

まずベクトル空間の定義は集合$VV$に対して，演算

• ベクトル和

$$+:V×V→V(a,b)↦+(a,b):=a+b+:V\times V\to V \\ (\bm a,\bm b)\mapsto +(\bm a,\bm b):=\bm a+\bm b$$

• スカラー積

$$∗:K×V→V(k,a)↦∗(k,a):=ka*:\mathbb K \times V\to V \\ (k,\bm a)\mapsto*(k,\bm a):=k\bm a$$

が以下の条件を満たすことである．

$$∀k,l∈K,∀a,b,c∈V(a+b)+c=a+(b+c)a+b=b+a∃!0∈V s.t. a+0=0+a=a∃!(−a)∈V s.t. a+(−a)=0k(a+b)=ka+kb(k+l)a=ka+la(k∗l)a=k(la)∃!1∈K s.t. 1a=a\forall k,l \in \mathbb K,\forall \bm a, \bm b, \bm c\in V \\ (\bm a+\bm b)+\bm c=\bm a+(\bm b+\bm c) \\ \bm a +\bm b = \bm b + \bm a \\ \exists! \bm 0\in V \ \text{s.t.}\ \bm a+\bm 0 = \bm 0 + \bm a = \bm a \\ \exists! \bm (-a)\in V\ \text{s.t.} \ \bm a+(-\bm a)=\bm 0 k(\bm a+\bm b)=k\bm a+k\bm b \\ (k+l)\bm a=k\bm a+l\bm a \\ (k*l)\bm a=k(l\bm a) \\ \exists! 1\in \mathbb K \ \text{s.t.}\ 1\bm a=\bm a$$

さらに，ベクトルの成分が実数や複素数の和・積（体$K\mathbb K$）であるならば，ゼロ元や可換性などが保証されるため，以下のように条件を絞れる．

$$∀a,b∈V,a+b∈V∀k∈K,∀a∈V,ka∈V\forall \bm a,\bm b\in V, \bm a+\bm b\in V \\ \forall k\in \mathbb K, \forall \bm a \in V , k\bm a\in V$$

（大学の試験ではこの条件が使われるのだが，本当に体を使うという条件でよいかが少しあいまい）
以下，体$KK$として実数$R\R$をとる

線形写像

線形写像$ff$の定義は以下のような条件を満たす写像である．

$$f:V→Wf(a+b)=f(a)+f(b)f(ka)=kf(a)f:V\to W \\ f(\bm a+\bm b)=f(\bm a)+f(\bm b) \\ f(k\bm a)=kf(\bm a)$$

以上の性質を準同型と言ったりする．fで写す前に足すのと，fで写した後に足すのが等しいことが重要だそうだ．詳しくは圏論を参照されたい．今回はあまり関係ない．圏論を布教したいだけ．

表現行列

上記のような線形写像の定義と，ベクトル空間の定義による線形結合を使えば，線形写像は行列演算で表現できることがわかる．
数学的にいうと，任意の$ff$について，ただ一つの表現行列$AA$が定まり，以下のように変換できる．

$$∀f:V→W,∃!A∈Rm×ns.t.[f(ei)]=[dj]AAx=yf(v)=[dj]Ax\forall f:V\to W, \exists! A\in\R^{m\times n}\\ \text{s.t.}\\ [f(\bm e_i)]=[\bm d_j]A\\ A\bm x=\bm y\\ f(\bm v)=[\bm d_j]A\bm x$$

この証明には，どう基底をとるか問われてくるので一度記法のルールを定めよう．

今回の記法ルール

お察しの通り筆者独自記法を含みます．

$$任意のベクトル：v,w任意のスカラー：c,d任意の基底：e,d成分：xi,yi成分ベクトル：x,y標準（正規直交）基底：e^iv=∑i=1nxiei=xiei∈V,Vの基底：{ei}=BVw′=∑j=1myjdj∈WWの基底：{di}=BW線形写像：f:V→Wv↦f(v):=w各次元：dim⁡V=n→dim⁡W=m行ベクトル：[ei]:=[e1,e2,...,en] \begin{align*} 任意のベクトル&：\bm v,\bm w\\ 任意のスカラー&：c,d\\ 任意の基底&：\bm e,\bm d\\ 成分&：x_i,y_i\\ 成分ベクトル&：\bm x,\bm y\\ 標準（正規直交）基底&：\bm {\hat e_i}\\ \bm v=\sum_{i=1}^nx_i\bm e_i&=x_i\bm e_i\in V, \\ Vの基底：\{\bm e_i\}&=B_V \\ \bm w'=\sum_{j=1}^my_j\bm d_j&\in W \\ Wの基底：\{\bm d_i\}&=B_W \\ 線形写像：f:V&\to W \\ \bm v&\mapsto f(\bm v):=\bm w \\ 各次元：\dim V=n&\to\dim W=m \\ 行ベクトル&：[\bm e_i]:=[\bm e_1, \bm e_2,...,\bm e_n] \end{align*}$$

成分ベクトルについて補足しておこう．
成分ベクトルxはvではないのだろうか？以下のようにすると

$$v=∑i=1nxiei=xiei=[ei]xx:=vとすればv=[ei]v\bm v=\sum_{i=1}^nx_i\bm e_i=x_i\bm e_i=[\bm e_i]\bm x\\\bm x:=\bm vとすれば\\ \bm v=[\bm e_i]\bm v$$

のように，見た目的に基底ベクトルの行列が生まれる．標準基底であればそこ部分は単位行列だし問題ないが，今回は任意の基底（正規化されてないし直交でもない）を使っているので，分かりやすくするため，あえて分けた．

表現行列の形・証明

上記の記法を用いて表現行列を導出してみる．
正直，双対空間の項まで読み飛ばして問題ない

$$v=x1e1+x2e2+...+xnenf(v):=w=y1d1+y2d2+...+ymdm \begin{align*} \bm v&= x_1\bm e_1+x_2\bm e_2+...+x_n\bm e_n \\ f(\bm v):=\bm w&=y_1\bm d_1+y_2\bm d_2+...+y_m\bm d_m \end{align*}$$

$$f(e1)=a11d1+a21d2+...+am1dmf(e2)=a12d1+a22d2+...+am2dm⋮f(en)=a1nd1+a2nd2+...+amndm[f(e1),f(e2),...,f(en)]=[d1,d2,...,dm](a11a12...a1na21a22...a2n⋮⋮⋱⋮am1am2...amn)[f(ei)]=[dj]A f(\bm e_1)=a_{11}\bm d_1+a_{21}\bm d_2+...+a_{m1}\bm d_m \\ f(\bm e_2)=a_{12}\bm d_1+a_{22}\bm d_2+...+a_{m2}\bm d_m \\ \vdots \\ f(\bm e_n)=a_{1n}\bm d_1+a_{2n}\bm d_2+...+a_{mn}\bm d_m \\ [f(\bm e_1),f(\bm e_2),...,f(\bm e_n)]=[\bm d_1,\bm d_2,...,\bm d_m] \begin{pmatrix} a_{11} & a_{12} & ... & a_{1n}\\ a_{21} & a_{22} & ... & a_{2n}\\ \vdots & \vdots & \ddots & \vdots \\ a_{m1} & a_{m2} & ... & a_{mn} \end{pmatrix} \\ [f(\bm e_i)]=[\bm d_j]A$$

のように基底の写す先の列ベクトル（＝行列）は，左からAをかけて表現できる．
次に座標は

$$f(v)=wf(x1e1+x2e2+...+xnen)=y1d1+y2d2+...+ymdmx1f(e1)+x2f(e2)+...+xnf(en)=y1d1+y2d2+...+ymdm[f(e1),f(e2),...,f(en)](x1x2⋮xn)=[d1,d2,...,dm](y1y2⋮ym)[f(ei)]x=[dj]y[dj]−1([dj]A)x=yAx=y \begin{align*} f(\bm v)&=\bm w \\ f(x_1\bm e_1+x_2\bm e_2+...+x_n\bm e_n) &=y_1\bm d_1+y_2\bm d_2+...+y_m\bm d_m \\ x_1f(\bm e_1)+x_2f(\bm e_2)+...+x_nf(\bm e_n) &=y_1\bm d_1+y_2\bm d_2+...+y_m\bm d_m \\ [f(\bm e_1), f(\bm e_2),...,f(\bm e_n)] \begin{pmatrix} x_1 \\ x_2\\ \vdots \\x_n \end{pmatrix} &=[\bm d_1,\bm d_2,...,\bm d_m] \begin{pmatrix} y_1\\ y_2\\ \vdots \\y_m \end{pmatrix} \\ [f(\bm e_i)]\bm x &= [\bm d_j]\bm y \\ [\bm d_j]^{-1}([\bm d_j]A)\bm x &= \bm y \\ A\bm x &= \bm y \end{align*}$$

よって，成分（座標）は左からAを書けることで変換できる．
以上を合わせれば任意のベクトルvを写すときは，

$$f(v)=[dj]y=[dj]Ax f(\bm v)=[\bm d_j]\bm y=[\bm d_j]A\bm x$$

とかける．

余談：線形写像もベクトル空間

ここで線形写像の集合$f,g∈Mf,g\in M$を用意し，線形写像のベクトル和・スカラー積を以下のように定義してみる．

$$+:M×M→M(f,g)↦+(f,g):=(f+g)(f+g)(a):=f(a)+g(a)+:M\times M\to M\\(f,g)\mapsto +(f,g):=(f+g) \\ (f+g)(\bm a):= f(\bm a)+g(\bm a)$$

$$∗:K×M→M(c,f)↦∗(c,f):=cf(cf)(a):=c(f(a))*:\mathbb K \times M\to M\\(c,f)\mapsto*(c,f):=cf \\ (cf)(\bm a):=c(f(\bm a))$$

これに対して，以下のようにベクトル空間の条件を満たすか確認する．

$$∀f,g∈M,f+g∈M∀c∈K,∀f∈M,cf∈M\forall f,g\in M, f+g\in M\\\forall c\in \mathbb K, \forall f \in M , c\bm f\in M$$

少し厄介なのは，あらゆる入力に対して成り立つか調べなければならないので4パターン調べる必要がある．
ちょっと疲れてきたので証明はこちらに任せると，線形写像そのものもベクトル空間であるといえる．
最後まで書いてから分かったのだが，ここはあまり必要ではない．
線形写像が行列で表現できるなら，行列は成分を持ったベクトル空間と見ることが出来るから，いわゆる自明と言える．

双対空間

ここからが本題で，共変・反変は双対空間を見ると現れる．

準備

線形汎関数と呼ばれる，ベクトル空間のベクトルcから実数空間Rのスカラーcへと写す線形写像の集合を考えてみる．
気持ちとしては，共変反変の成分はスカラーなので，ベクトルvから成分v_iを取る写像を見つけてみたいというモチベーションで行こう．

$$v=∑i=1nxiei∈V{e1,e2,...,en}=BVc∈R{d}=BR \bm v=\sum_{i=1}^n x_i\bm e_i \in V\\ \{\bm e_1, \bm e_2,...,\bm e_n\}=B_V \\ c\in\R\\ \{d\}=B_{\R}$$

線形汎関数は

$$f:V→Rf(v):=c f:V\to\R \\ f(\bm v):=c$$

線形汎関数の集合は

$$f,pi∈V∗:=hom⁡(V,R) f,p_i\in V^*:=\hom(V,\R)$$

とする．p_iとかは後で出てくるのでお待ちください．

導出

変換行列$AA$を用いて，

$$f(v)=[dj]Ax=d[a1,a2,...,an](x1x2⋮xn)=da⋅x=(dai)xidai:=fi∈Rとするxi:=pi(v)∈V∗とするとf(v)=fipi(v)よってf=fipi基底は：{p1,p2,...,pn}=BV∗ f(\bm v)=[\bm d_j]A\bm x=d[a_1, a_2, ...,a_n]\begin{pmatrix} x_1\\ x_2\\ \vdots\\ x_n \end{pmatrix}=d\bm a\cdot\bm x=(da_i)x_i \\ da_i:=f_i\in\Rとする \\ x_i:=p_i(\bm v)\in V^*とすると \\ f(\bm v)=f_ip_i(\bm v) \\ よって \\ f=f_ip_i \\ 基底は：\{p_1,p_2,...,p_n\}=B_{V^*}$$

ここで，基底関数：$pip_i$に着目すると，この関数はベクトルの標準成分を取り出す関数である．これは元基底$eie_i$と直交する基底との内積（を正規化したもの）に等しい．
そこで，$ei\bm e_i$に直交する基底：$ei\bm e^i$　を導入する！
上下の添え字の違いを$pp$や$xx$にも反映させる定義に変更して

$$ei⋅ej∣ei∣∣ej∣=δijpi(v):=v⋅ei∣ej∣∣ei∣=xjej∣ej∣⋅ei∣ei∣=xjδji=xi \frac{\bm e_i\cdot\bm e^j}{|\bm e_i||\bm e^j|}=\delta_i^j \\ p^i(\bm v):=\bm v\cdot\frac{\bm e^i}{|\bm e_j||\bm e^i|} =x_j\frac{\bm e_j}{|\bm e_j|}\cdot\frac{\bm e^i}{|\bm e^i|}=x_j\delta_j^i=x^i$$

よって，もうめんどくさいので正規化されたもので考え直すと

$$pi(v):=ei⋅vf(−)=fipi(−)=fiei⋅(−)∈V∗v=xiei∈V p^i(\bm v):=\bm e^i\cdot\bm v \\ \bm f(-)=f_i\bm p^i(-)=f_i\bm e^i\cdot(-)\in V^* \\ \bm v=x^i\bm e_i\in V$$

以上より，元の基底と直交する基底$ei\bm e^i$の成分$fif_i$が得られた．

結論

上記議論から，

$$共変ベクトル（共変成分・反変基底）：v=viei∈V∗反変ベクトル(反変成分・共変基底)：v=viei∈V 共変ベクトル（共変成分・反変基底）：\bm v=v_i\bm e^i\in V^* \\ 反変ベクトル(反変成分・共変基底)：\bm v=v^i\bm e_i\in V$$

と定義する．

そして，共変・反変は，内積が直交を前提とした演算であるから生じる．
任意の基底では，

$$ei⋅ej∣ei∣∣ej∣≠δij \frac{\bm e_i\cdot\bm e_j}{|\bm e_i||\bm e_j|}\neq\delta_{ij}$$

となり内積で成分が得られない．しかも得られたとしてもそれは直交で見た成分だから，共変・反変が生じる

幾何で見る共変・反変

すみません力尽きてきたので，以下はその都度追記していきます．

共変の例：勾配ベクトル

$$∇f=∂f∂x′i=∂xj∂x′i∂f∂xj=∂x1∂x′i∂f∂x1+∂x2∂x′i∂f∂x2+∂x3∂x′i∂f∂x3 \nabla f=\frac{\partial f}{\partial x'^i}=\frac{\partial x^j}{\partial x'^i}\frac{\partial f}{\partial x^j} \\ =\frac{\partial x^1}{\partial x'^i}\frac{\partial f}{\partial x^1} +\frac{\partial x^2}{\partial x'^i}\frac{\partial f}{\partial x^2} +\frac{\partial x^3}{\partial x'^i}\frac{\partial f}{\partial x^3}$$

$$vi′=∂xj∂x′ivjvi′=aijvj \bm v'_i=\frac{\partial x^j}{\partial x'^i}\bm v_j \\ \bm v'_i=a^{ij}\bm v_j$$

反変の例：微小変位ベクトル

微小変位ベクトルは，基底$eie_i$で考えるとき，$dx:=dxieid\bm x:=dx^i\bm e_i$のように書ける．これに座標変換をかませば，偏微分の連鎖律により

$$dx′i=∂x′i∂xjdxjdx′i=aijdxjdx'^i=\frac{\partial x'^i}{\partial x^j}dx^j \\ dx'^i=a_{ij}dx^j$$

と書ける．

余談

どこにも明記されていないのだが，どうやら
問題で与えられた・考えるときに見る基底ベクトルを共変基底ベクトルにしているようだ．
そして，その双対基底ベクトルを反変基底ベクトルにしている．

っぽいのだが，明記された文献を見つけられなかった．
よって，与えられた基底ベクトル＝共変基底ベクトルと仮定している．

テンソルと不変量

力尽きました．

改めて共変反変とは何か

• 歪んだ座標系・基底において，
• 内積のように，垂直（直交）な線を見て成分を得よう
  としたら出てくる概念である．