Fract'ol - How to zoom to the limit
Assignment
The assignment is to draw a fractal, but that is just the subject matter, as stated in the PDF, the purpose of this assignment is to learn about optimization and event handling.
What this document will explain
This article considers how to implement the following two requirements of the assignment
- The mouse wheel zooms in and out, almost infinitely (within the limits of the computer)*.
- The management of your window must remain smooth
"The limits of the computer" is interpreted in this document as "the limit of the number of doubles that can be represented by the computer".
What this document does NOT explain
There are various articles on how to write fractals, so I will not explain them here.
Common Examples of Poor Implementation
1. Stopping the Calculation Midway

One of the key characteristics of fractals is self-similarity. If you stop the calculation midway, you won't be able to see the smaller Mandelbrot sets, resulting in a fractal that lacks self-similarity.
2. Screen Freezing

It’s understandable that calculating details takes time. However, if implemented naively, the screen may freeze. If a rainbow cursor (or hourglass) appears "even for a moment", or if the screen becomes unresponsive and can't be closed even when clicking the close button, it is considered a poor implementation.
Goal
Due to the limitation of using only one thread as specified in the task, rendering will take time as you zoom in. However, the aim is to create a fractal that remains responsive and doesn't freeze, allowing for smooth operation even when zoomed to the limit.
In this article, the goal is to enable smooth zooming up to hundreds or thousands of trillions of times magnification.
Conflicting requirements
- Need to compute infinitely many times to draw a fractal
- The screen needs to operate smoothly without freezing
Now how to solve these two conflicting requirements is the point of this assignment.
Units of measure that are important
FPS: Number of images (frames) displayed per second
FLOPS: Number of floating point operations per second
What is a smooth running app?
Video is made to look like a moving picture by drawing images one after another like a flip book.
Most videos are 30 FPS (or 60 FPS). In other words, 30 pictures are displayed per second.
In other words, if we stop the calculation at one frame (1/30 = 33 milliseconds), display an image, and return an event (mouse operation, etc.) to the user, we can make it look as if it is runing smoothly.
When making a game or creating a UI for an application, it is very important for the user experience whether or not the computation is completed within one frame. I think this assignment is not only about drawing fractals, but also about learning to do so.
How to interrupte the calculation within 33 milliseconds
The number of times a computer can perform a calculation per second is expressed in FLOPS, but since threads cannot be used this assignment, it is sufficient to know that the number is roughly proportional to the number of CPU clocks.
Recent CPU clock speeds are around 2~3GHz. The detailed number is not so important, as long as the approximate order (number of digits) is correct, there is no problem.
For now, assuming that the CUP is 2GHz, the number of operations that can be performed within 1/30 second(33 milliseconds) can be roughly estimated as follows.
In other words, counting the number of calculations and once 66 million times calculations have been made, the process can be stopped, the image in the middle of the calculation can be displayed, and events (such as mouse operations) can be returned to the user for smooth operation without the screen getting stuck.
Estimating the number of calculations
The heaviest processing part of the Mandelbrot and Julia set calculations is the loop to determine whether the asymptotic expressions diverge or not.
The asymptotic formula would roughly look like this code.
tmp = z[0] * z[0] - z[1] * z[1] + c[0];
z[1] = 2.0 * z[0] * z[1] + c[1];
z[0] = tmp;
How many floating-point operations are there in this code if we do the calculations in a straightforward manner?
Let's count them.
Real part
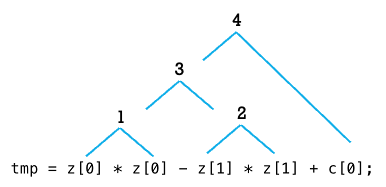
Imaginary part

The real part is calculated
The number of times that the asymptotic formula can be calculated within one frame (1/30 second) is
Well, we estimate it to be about
(I wrote roughly
Using loop hook of minilibx
Use the loop hook (mlx_loop_hook) to continue the calculation while returning events to the user.
The number of times each pixel has been calculated is added up, the number of pixels processed is stored, and the process is aborted after 10 million incremental calculations. Return an event to the user.
Then, the next minilibx loop hook computes the continuation.
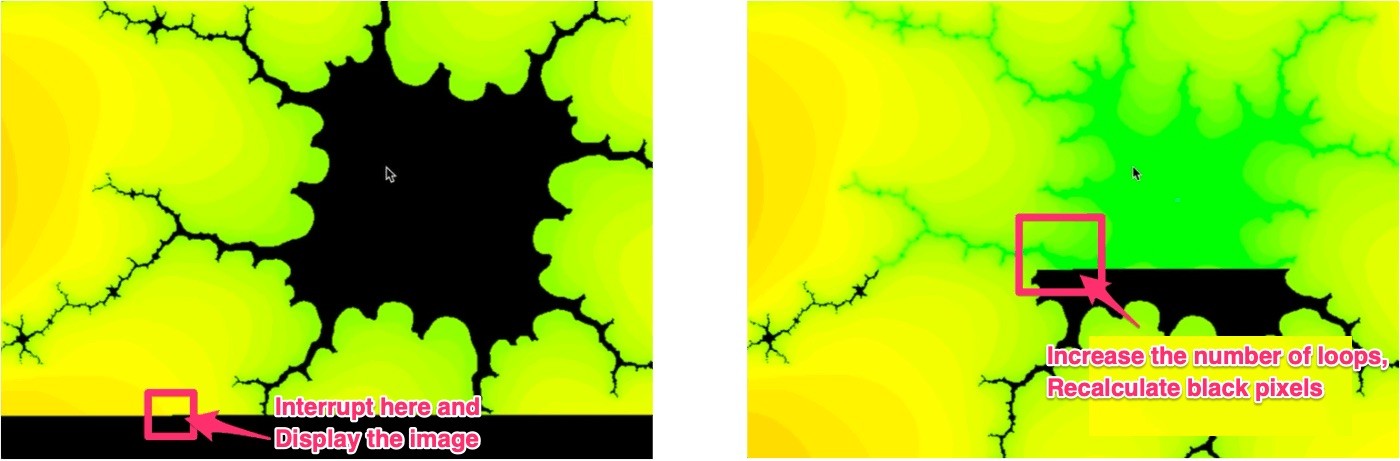
Calculate details while increasing the number of judgments
At first, set the number of times to judge the divergence of an incremental expression to about 50 times, and when you have finished calculating to the last pixel, increase that number of times and recalculate the pixels that did not diverge (black pixels), you can operate smoothly and zoom to the limit of floating point.
Using Optimization Flags
If you're not using optimization flags, rebuild the program with the flags enabled (e.g., make re).
There are various optimization flags available. Probably "-O2" is sufficient to achieve good performance. (Note: "-O2" uses a capital "O" followed by the number 2. It's not the number zero-two.)
CFLAGS=-Wall -Wextra -Werror -O2
The Limitations of Double-Precision Floating-Point (double)
I may have skipped some explanations, so it might be a bit difficult to understand.
If implemented correctly, you should be able to achieve smooth zooming up to around hundreds or thousands of trillions in magnification.
So why does the image become pixelated when zooming beyond hundreds of trillions of times?
The maximum value that can be represented by a double is (10^{308}) (a 1 followed by 308 zeros).
A thousand trillion (1,000,000,000,000,000) is (10^{15}), which is much smaller than the maximum value of a double.
The issue lies in the precision of double, which is limited to 14–15 significant digits (in decimal). Calculations requiring precision beyond 14–15 digits are rounded, introducing errors. These errors are called rounding errors.
My fract'ol
Mandelbrot Set
Julia Set
Sierpinski Gasket
(Appendix) How to use minilibx
Tutorial
Tutorial on how to use minilibx
Sample project
This is a sample that drawings and hooks. When executed, it looks like this.

If you like, you can also read here
Let's write Get_Next_Line(GNL) in 1 hour
And with only three functions (of course, following Nominette).
↓ Press the ♡


Discussion