fract'ol(前編) 〜サクサク動いて限界まで拡大する方法〜
by 課題のハードルを上げようの会
課題
課題はフラクタルを描くことですが、それはただの題材であって、PDFに書いてある通り、この課題の"目的"は最適化とイベントハンドリングについて学ぶことだと思っています。
この資料で説明すること
課題にある下記2つの要件を実現する方法を考えます。
- The mouse wheel zooms in and out, almost infinitely (within the limits of the computer)※.
マウスでほぼ無限に(コンピューターの限界の範囲内で)ズームインとアウトできること、 - The management of your window must remain smooth
スムーズにウインドウ操作ができること
※この資料ではthe limits of the computer を「doubleで表現可能な数値の限界」と解釈しています。
この資料で説明しないこと
フラクタルの書き方については、色々な資料があるので、ここでは説明は省略します。
minilibxの使い方が分からない方はコチラ
よく見かける悪い例
1. 途中で計算を止めている

フラクタルの特徴として自己相似性があります。途中で計算を止めてしまうと、小さなマンデルブロ集合を見ることができず、自己相似的になりません。
2. 画面が固まる

細部まで計算すると、計算時間がかかるのは仕方ありません。
しかし、愚直に実装すると画面が固まってしまいます。"一瞬でも"レインボーカーソル(砂時計)が表示されたり、バツボタンを押しても、画面が固まって閉じられないものは悪い例となります。
目標
課題の制限で使えるスレッドが1個しかないため拡大していくと描画に時間はかかりますが、限界まで拡大しても、画面は固まらずに、サクサク(ヌルヌルとは言っていない)動くフラクタルを描画できるようにしたいと思います。
この記事では数百兆〜数千兆倍までスムーズに拡大できるようにすることを目標とします。
相反する要件
- フラクタルを描画するためには無限回計算する必要がある
- 画面が固まらずにスムーズに操作できる必要がある
さてこの2つの矛盾する要件をどのように解決するのか、ということがこの課題のポイントとなります。
重要となる単位
FPS: 1秒間に表示する画像(フレーム)の数
FLOPS: 1秒間に処理できる浮動小数点演算の回数
サクサク動くとは
動画はパラパラ漫画のように次々に画像を描画することで、絵が動いているように見せています。
動画は約30FPS(多いと60FPS)となっています。つまり1秒間に30枚の絵を表示しているということです。(映画だと24FPSだったりします)
今回、画面がサクサク動いているように見せるため、30FPSを目指します。
つまり、1フレーム(1/30秒 = 33ミリ秒)で一旦計算を中断し、画像を表示して、ユーザーにイベント(マウスなどの操作)を返すようにすれば、サクサク動いているように見せることができます。
ゲームを作ったり、アプリのUIを作る際、1フレーム以内に計算が終わるかどうか、というのはユーザー体験としてとても重要なことになります。この課題は単にフラクタルを描くだけでなく、それを学ぶ課題だと思います。
33ミリ秒以内に一旦計算を中断させる方法
パソコンが1秒間に計算できる回数はFLOPSという単位で表されますが、今回スレッドなどは使用できないため、大体CPUのクロック数に比例する数だということだけ分かっていれば大丈夫です。(SIMD命令によって数倍早い可能性がありますが、一旦少なめに見積もります。)
最近のCPUのクロック数は2~3GHz前後となります。細かい数字はあまり重要ではなく、大体のオーダー(桁数)が合っていれば問題ありません。
とりあえずCUPが2GHzとして、1/30秒(33ミリ秒)以内に演算できる回数はおおよそ下記のように見積もることができます。
つまり、計算回数を数えて6,666万回計算したら一旦処理を中断し、一旦計算途中の画像を表示して、イベント(マウス操作など)をユーザに返せば、画面が固まらずにスムーズに操作できるようになります。
計算回数の見積もり
マンデルブロ集合やジュリア集合の計算で一番処理が重いのは漸化式が発散するかどうか判定するためのループです。
漸化式は大体、こんな感じのコードになると思います。
tmp = z[0] * z[0] - z[1] * z[1] + c[0];
z[1] = 2.0 * z[0] * z[1] + c[1];
z[0] = tmp;
愚直に計算する場合、このコードに浮動小数点演算は何回あるでしょうか?
では数えてみましょう。
実部

虚部
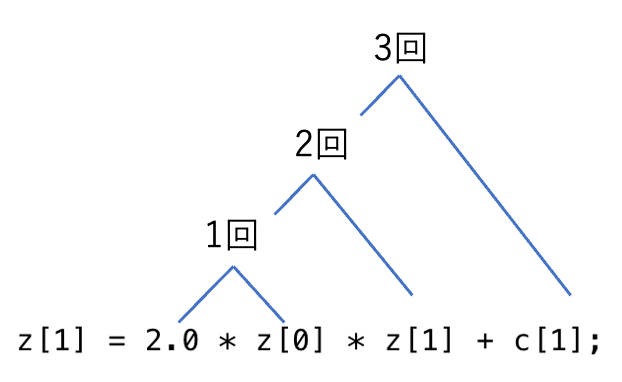
実部が4回、虚部が3回で合計7回。
1回漸化式を計算するのに、浮動小数点演算が7回必要となり、1/30秒で計算できる回数が6,666万回のため、
1フレーム(1/30秒)以内に漸化式を計算できる回数は952万回。
まぁ、大体1,000万回ぐらいと見積もります。
(だいたい1,000万回と書きましたが、先に書いた通りかなり雑な見積もりです。SIMD命令や、そもそもCPUのクロック数がもっと高いかもしれないので、もっと計算できるかもしれないし、逆に関数呼び出し時のオーバーヘッドや、画像表示などループ以外にも処理があるため、もっと少ないかもしれません。その辺は適当にチューニングして下さい。)
minilibxのループフックの使用
ユーザにイベントを返しつつ、計算を続けるにはループフック(mlx_loop_hook)を使用します。
1ピクセルごどに何回回計算したか積み上げて、1,000万回漸化式を計算したら、処理を中断し、何ピクセル目まで処理したか保存しておきます。一旦ユーザーにイベントを返して、次のminilibxのループフックで続きを計算する、ということを繰り返します。
判定回数を増やしながら細部を計算
最初、漸化式の発散を判定する回数を50回程度にしておき、最後のピクセルまで計算し終わったら、その回数を増やして、発散しなかったピクセル(黒いピクセル)を再計算していけば、サクサク動いて浮動小数点の限界までズームできるようになります。

最適化フラグを使用
もし最適化フラグを使っていないなら、フラグを付けて再ビルド(make re)して下さい。
最適化フラグは色々ありますが、-O2ぐらいで十分なパフォーマンスがでます(-O2は大文字のオーに数字の2です。ゼロ2じゃないよ)。
CFLAGS=-Wall -Wextra -Werror -O2
最適化は色々あるので調べてみて下さい。-march=nativeとかはとりあえずつけてみてもいいかもしれません。
倍精度浮動小数点(double)の限界
結構説明を端折ってしまったので、分かりづらくなってしまったかもしれませんが、うまく実装できていれば、だいたい数百兆〜数千兆倍までスムーズに拡大できるようになります。
では、なぜ数百兆倍までズームすると画像が粗くなってしまうのでしょうか?
doubleで表現できる最大値は10の308乗(1の後ろに308個ゼロが続く)です。
1000兆は10の15乗(1,000,000,000,000,000)なので、doubleの最大値よりずっと小さいです。
それはdoubleで表現できる精度に14〜15桁(10進数換算)の限界があるためです。14〜15桁以上の精度の計算は端数処理され、誤差が発生してしまいます。その誤差の事を丸め誤差と呼びます。
丸め誤差について
丸め誤差について書こうと思ったけど、力尽きたので後で書きます。ググって下さい。
フラクタルの動画
マンデルブロ集合
ジュリア集合
シェルピンスキーのギャスケット
(補足)minilibxの使い方について
サンプルプロジェクト
とりあえずminilibxを動かしてみたい方はこちら
描画とhookを一通り使ったサンプルになります。実行するとこんな感じになります。

チュートリアル
minilibxの使用方法に関するチュートリアル
おまけ
Discussion