Optimal Transport Conditional Flow Matching - 拡散モデルに取って代わる次世代の生成技術？

こんにちは！Fusic 機械学習チームの鷲崎です。最近、音声や言語処理に興味がありますが、機械学習モデルの開発からMLOpsまでなんでもしています。もし、機械学習で困っていることがあれば、気軽にDMください。

本記事では、Flow Matching (FM)と、その発展版であるOptimal Transport Conditional Flow Matching (OT-CFM)を解説します。最近の生成AIでは、拡散モデルがよく使用されていますが、Flow Matchingは、拡散モデルに取って代わる可能性がある生成技術と考えています。

おもに、Improving and Generalizing Flow-Based Generative Models with Minibatch
Optimal Transportという論文を参考に解説していきたいと思います。また、本記事の図は、論文から参照いたしました。

Flow Matachingは、音声合成においては、Metaが発表した音声合成手法であるVoiceboxや、より高速で高性能な音声合成手法であるMatcha-TTSに使用されてきています。
Matcha-TTSに関しては、弊社のToshikiが、記事を書いているので、ぜひ、読んでみてください。

【音声合成】Matcha-TTS🍵で日本語音声を生成してみる

個人的に、Flow Matchingは、拡散モデルが発展した手法と考えて論文を読み始めたのですが、それだとかなり勘違いしてしまっていました。皆さん、Normalize Flowという手法を聞いたことがありますでしょうか？現在、拡散モデルがバズワード化しすぎて、あまり耳にしないかもしれませんが、分布を変換する関数を学習するとてもおもしろいモデルです。そのNormalize Flowの発展版がFlow Matchingと考えるとスムーズに納得できた気がします。

そこで、本記事では、拡散モデルとNormalize Flowの関係性からFlow Matchingまでの過程とその発展を解説していきたいと思います。

理解が及ばなかった部分が多々あるため、ご指摘をたくさんいただけると嬉しいです。よろしくお願いいたします。

基礎

Flow Matchingを理解するために、まず、拡散モデルの拡散過程を連続時間化した、確率微分方程式(SDE)を説明します。そして、それを常微分方程式(ODE)に変換した確率フローODEを説明します。

その後、確率フローODEが、Normalize Flow (NF)を連続化したContinuous Normalize Flow (CNF)と、どのように関連するか説明します。

SDEとODEの詳細に関しては、拡散モデル データ生成技術の数理という本がとても参考になります！ぜひ読んでみてください。

拡散モデルの確率微分方程式(SDE)

拡散モデルでは、拡散・逆拡散過程のステップ数を増やせば増やすほど、離散化誤差が小さくなり生成性能が向上します。そこで、ステップ数を無限大に増やして連続化した場合の拡散モデルを考え、このモデルは確率微分方程式(SDE)とみなすことができます。

拡散過程に相当する拡散SDEは、以下の式で与えられます。

$dx = f(x, t)dt + g(t)dw$

$dx$はデータ$x$の微小時間あたりの変化量です。この変化量は、決定的に変化する量$f(x, t)dt$と、ランダムに変化する量$g(t)dw$からなります。$f(x, t)$は、データ$x$と時刻$t$で決まります。また、$w$は、標準ウィーナー過程と呼ばれ、$dw$は、微小時間間隔$\tau$において、平均$0$、分散$\tau$となる正規分布です。

一方で、逆拡散過程は、以下のSDEで与えられます。

$dx = [ f(x, t) - g^2(t) \nabla_x \rm{log} p_t (x) ] dt + g(t) d \bar{w}$

時刻$t$のスコア$\nabla_x \rm{log} p_t (x)$が、わかりさえすれば、事前分布$p_T(x)$から、データ分布$p_0(x)$への変換経路を求めることができます。

Denoising Diffusion Probabilistic Model (DDPM)の場合

元のDDPMの式は、以下です。

$x_{t+1} = \sqrt{1 - \beta_{t}}x_{i-1} + \sqrt{\beta_i} z_{i-1}$

この式を、SDEに変換した場合、以下のようになります。

$dx = -\frac{1}{2}\beta(t)xdt + \sqrt{\beta(t)}dw$

ここでの、$\beta$は、ノイズスケジュールのパラメータです。

確率フロー常微分方程式 (ODE)

任意のSDEは、同じ周辺分布$\lbrace p_t(x) \rbrace_{t\in \lbrack 0,T \rbrack}$を持つ常微分方程式(ODE)に変換することができ、以下の式で表されます。

$dx = \lbrack f(x, t) - \frac{1}{2}g^2(t) \nabla_x \rm{log} p_t (x) \rbrack dt$

確率的な要素が除外され、拡散過程では$dx$, 逆拡散過程では$-dx$のように、同じ式で取り扱うことができます。

Normalizing Flow

Normalizing Flow (NF)は、複雑な分布を、より単純な分布へ変数変換（Normalize)する関数です。

例えば、シンプルな確率密度関数$p_Z(z)$と、複雑な確率密度関数$p_Y(y)$の間の変数変換を行うとします。そのとき、変数$z$から$y$への変数変換を$y=f(z)$としたとき、確率密度関数$p_Y(y)$は、以下の式で表せます。

$p_Y(y) = p_Z(z) | \rm{det} \frac{\partial f^{-1}}{\partial y} | = p_Z(z) | \rm{det} \frac{\partial f}{\partial z}|^{-1}$

NFでは、この変数変換を行う関数$f$は、可逆（$z = f^{-1}(y)$）であるという性質を満たします。

また、NFでは、この性質をもつ関数$f_i$による合成関数で、変数変換の式を表しています。

$f = f_1 \circ f_2 \circ \dots \circ f_N$

$f^{-1} = f^{-1}_N \circ \dots \circ f^{-1}_1$

ざっくりしたイメージですが、$f_i$で徐々に分布を変換していくのが、ノイズを除去していく拡散モデルに似ている気がしました！！一方で、拡散モデルは、ノイズから生成していますが、NFは、分布から生成していくという利点がある気がします。

Continuous Normalizing Flow

Neural Ordinary Differential Equations (Neural ODE) という論文で、連続時間化したNormalizing Flow を Continuous Normalizing Flow (CNF)と呼んでいました。

Neural ODEでは、Residual Networkのように、残差を計算の結果を元の値に付加することで値を更新する方法に着目し、以下のように常微分方程式の式に似た概念を導入しています。

$x_{t+1} = x_t + \frac{df(x)}{dt} = x_t + f(x, t)$

この表現を用いる利点は、時刻も入力としたことで、変化量の微分を表す単一のネットワークを使用すればよく、メモリの使用量を削減できます。加えて、逆変換の計算が可能で、RNNなど離散的な時間を扱うモデルとはことなり、連続時間を扱うことができます。※これの特殊系が確率フローODEになります。

このNeural ODEの考えを用いて、時間連続性をもつNFであるContinuous Normalizing Flow (CNF)は、以下のように表されます。

$x_1 = x_0 + \int^{t_1}_{t_0} f(x(t), t) dt$

この式は、確率変数$x_0$から$x_1$の変化を、連続時間の変化量の積分で操作することができます。また、微分$dx/dt = f(x(t), t)$は、どの時間$t$においても、$f(x(t), t)$という単一のネットワークで表現されています。

また、この変換の逆変換も、以下のように書くことができます。

$x_0 = x_1 + \int^{t_0}_{t_1} f(x(t), t) dt$

上記のことから、拡散モデルの拡散過程と逆拡散過程に類似した表現をすると、拡散過程にあたるCNFでは、

$dx = f(x, t) dt$

となり、逆拡散過程にあたるCNFでは、

$dx = -f(x, t) dt$

のように表現できます。

なぜ、拡散モデルがよいとされているのか？

拡散モデルのDDPMの損失は、以下になります。

$\rm{E}_{t, q(z), p_t(x|z)} || s_{\theta}(t, x) - \nabla_x \rm{log} p_t(x|z)||^2_2$

この式の意味は説明しませんが、拡散モデルでは各時刻$t$ごとの生成過程を独立に学習可能であることがわかります。これは、複数のステップを繰り返すことで、巨大な計算過程を学習でき、かつ、計算グラフの一部分を抜き出して学習できるという利点があります。このようなアプローチをSimulation Freeと呼びます。

一方で、CNFの損失は、以下になります。

$\rm{E}_{q(x_1)} [ \rm{log} p_0(x_0) - \int \rm{Tr}(\frac{\partial f}{\partial x_t}) dt]$

見ての通り、全時刻に渡って積分した値を使用しており、計算グラフのすべてを使って学習が必要となる欠点があります。このようなアプローチは、Simulation based trainingと呼ばれます。これが原因で、学習効率が悪く、拡散モデルほど使用されていませんでした。

そこで、CNFの学習を改善したFlow Matchingが開発されました！

Flow Matching

CNFを安定して学習可能なFlow Matchingについて解説します。上記のように、時間全体の学習が必要である点が、CNFの欠点と言えます。そこで、CNFを時刻ごとに、学習可能にするために、Flow Matchingが、開発されました。

まず、微小時変ベクトル場$u$のODEは、以下になります。

$dx = u_t (x) dt$

$u_t(x)$は、$u(t, x)$と同様です。

また、密度$p_t$は、時刻$0$から時刻$t$まで$u$に沿って輸送される点$x$ ($x \sim p_0$)の密度です。
このとき、時変密度$p_t$が$\partial p / \partial t = - \nabla \cdot (p_t u_t)$であるとき、$p$は$u$による確率経路で、$u$は$p$のベクトル場となります。

かなり説明を省いていますので、詳細は論文を読んでいただきたいのですが、個人的に確率経路$p$は、初期条件の分布からデータ分布までの道のりを表現しており、ベクトル場$u$は、各時刻$t$において分布が移動する方向と距離を表現しているとイメージしています！なんとなくです...

Flow Matchingは、ニューラルネットワーク$v_{\theta}(t, x)$が、時間依存のベクトル場$u_t(x)$に回帰するような損失を持ち、以下のようになります。

$L_{FM}(\theta) = \rm{E}_{t\sim \mathcal{U}(0,1), x\sim p_t(x)} || v_{\theta}(t, x) - u_t(x)||^2$

Flow Matching for Generative Modeling では、正規分布によるガウス確率経路$p_t(x) = \mathcal{N}(x | u_t, \sigma_t^2)$を考え、ベクトル場は、以下のようになるとしています。

$u_t(x) = \frac{\sigma_t^{\prime}}{\sigma_t} (x - \mu_t) + \mu_t^{\prime}$

$\ast^{{\prime}}$は、微分を行っています。

Flow Matchingにより、このベクトル場を回帰するように$v_{\theta}(t, x)$を学習することで、時刻ごとの学習が可能になり、CNFの学習を安定して行えるようになりました。

Conditional Flow Matching

Flow matchingは、ガウス確率経路を仮定していました。そこで、ガウス分布の仮定を緩和し、2つの分布間の条件付き確率経路(ODE Bridge)の学習を可能にした、Conditional Flow Mataching (CFM)が提案されました。

潜在条件変数$z$において、潜在変数による分布$q(z)$と確率経路$p_t(x|z)$による周辺確率経路$p_t(x)$は、以下の式となります。

$p_t(x) = \int p_t(x|z)q(z)dz$

ベクトル場$u_t(x|z)$により初期条件分布$p_0 (x|z)$から確率経路$p_t(x|z)$が生成されるとした場合の周辺ベクトル場$u_t(x)$を、

$u_t(x) := \rm{E}_{q(z)} \frac{u_t(x|z)p_t(x|z)}{p_t(x)}$

とします。周辺ベクトル場$u_t(x)$により、初期条件$p_0(x)$から周辺確率経路$p_t(x)$が生成されます。
このとき、条件付き確率経路$p_t(x|z)$とベクトル場$u_t(x|x)$から$u_t$を計算したいのですが、分母の$p_t(x)$の計算は積分を含み困難です。

そこで、CFMの損失を

$\rm{L}_{CFM}(\theta) = \rm{E}_{t, q(z), p_t(x|z)} ||v_{\theta}(t, x) - u_t(x|z)||^2$

としたとき、特定の条件下で、

$\nabla \rm{L}_{CFM}(\theta) = \nabla \rm{L}_{FM}(\theta)$

であることが論文で示されました。
つまり、条件付きベクトル場$u_t(x|z)$を計算できるなら、周辺ベクトル$u_t(x)$に回帰するニューラルネット$v_{\theta}$を学習できることを示しました。

これをConditional Flow Matching(CFM)とし、以下のアルゴリズム(論文中 Algorithm 1)で計算されます。

これより下の項目では、$q(z)$, $p_t(-, z)$, $u_t(-|z)$によって定義される様々なCFMについて説明します。

Flow Matching from a Gauusian

Flow Matching for Generative Modeling で説明されたFlow MatchingをCFMの特殊なケースとして解釈した場合について説明します。

この論文では、$z = x_1$とし、標準正規分布$p_0(x|z) = \mathcal{N}(x; 0, 1)$から、データ分布$p_1(x|z) = \mathcal{N}(x; x_1, \sigma^2)$への確率経路を設定しています。つまり、確率経路は、

$p_t(x|z) = \mathcal{N}(x | tx_1, (t \sigma - t + 1)^2)$

となります。$t=0$の場合と、$t=1$の場合を考えれば、時刻を0から1に変化した場合の変化が想像できると思います。この、確率経路より、ベクトル場は、

$u_t(x|z) = \frac{x_1 - (1-\sigma)x}{1 - (1 - \sigma)t}$

となります。実は、このベクトル場は、確率経路の平均と分散を上記FMの章に記載したベクトル場の式

$u_t(x) = \frac{\sigma_t^{\prime}}{\sigma_t} (x - \mu_t) + \mu_t^{\prime}$

に当てはめると計算できます！

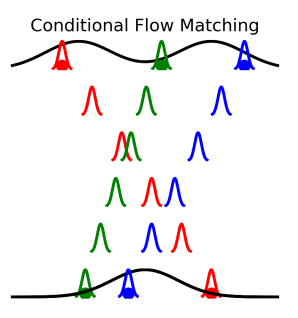
下図は、論文中のFigure 1で、Flow Matchingのイメージです。ガウス分布がデータサンプルへ分散を小さくしながら遷移している確率経路が見えますね。

Independet CFM

CFMの基本形として、初期点$x_0$と目標点$x_1$から潜在変数$z$を同定するとし、潜在分布$q(z)$を$q(z) = q(x_0)q(x_1)$としたI-CFMを説明します。
何を言いたいかというと、$x_1$だけでなく、$x_0$も用いた、確率経路を設定しています。$x_0$と$x_1$の間の確率経路をガウス分布の移動と考えると、以下の確率経路になります。

$p_t(x|z) = \mathcal{N}(x | tx_1 + (1 - t) x_0, \sigma^2)$

そして、この確率経路の平均と分散をベクトル場の定式(flow matchingの項に記載)にあてはめると、ベクトル場は、

$u_t(x|z) = x1 - x0$

となります。かなりシンプルな形式になっていますが、これにより$p_t(x|z)$は効率的にサンプリングでき、$u_t$は効率的に計算できるため、$\rm{L}_{CFM}$の勾配計算も効率的とのことです。

下図は、論文中のFigure 1で、I-CFMのイメージです。固定の分散の分布が移動している事がわかります。

I-CFMのアルゴリズムは、以下になります。これだけ見ると、かなりシンプルですね。

Optimal Transport CFM

まず、2-Wasserstein距離による最適輸送(OT)に関して説明します。そして、OTを用いてCFMに関して説明します。

2-Wasserstein距離

最適輸送問題は、ある測度から別の測度へのマッピングを、コストが最小化するように求めるものである。論文では、2-Wasserstein距離を用いており、分布$q_0$と$q_1$の間のコスト$c(x, y) = ||x - y||$ を用いて、以下の式で表されます。

$\mathcal{W}(q_0, q_1)^2_2 = \rm{inf} \int_{\mathcal{X}} c(x, y)^2 d \pi (x, y)$

そして、2-Wassrstein距離の動的形式は、ある測度を他の測度に変換するベクトル場$u_t$上の最適化問題としても定義できます。

$\mathcal{W}(q_0, q_1)^2_2 = \rm{inf} \int_{\rm{R}^d} \int^{1}_{0} p_t(x) ||u_t(x)||^2 dt dx$

L2正則化を持つCNFが動的最適輸送に近似可能なことは証明されていますが、この式の計算には、多くの積分とバックプロパゲーションが必要なため数値的にも、効率的にも問題がありました。そこで、CFMとして、直接ベクトル場を回帰することで、これらの問題を回避することが提案されました。

OT-CFM

上記の2-Wasserstein距離をCFMに当てはめるため、2-Wasserstein最適輸送写像$\pi$を$q(z)$とすることが提案されました。

$q(z) := \pi (x_0, x_1)$

これにより、$q_0$, $q_1$から、独立にサンプリングしていた$x_0$, $x_1$を、最適輸送写像によって、同時にサンプリングします。
I-CFMに対して、この修正を行ったものが、OT-CFMになります。

論文では、

OT-CFMは、$q(x_0)$と$q(x_1)$の間の静的OT写像と中間時間ステップで条件付きフローの回帰のみを用いて、シミュレーションフリー（時間ごとに学習可能）な動的OT問題を解いた最初の手法である。

とのことです。

下図は、論文中のFigure 1で、OT-CFMのイメージです。I-CFMと異なり、時刻$0$から$1$の分布の移動がOTのおかげでスムーズに見えます。

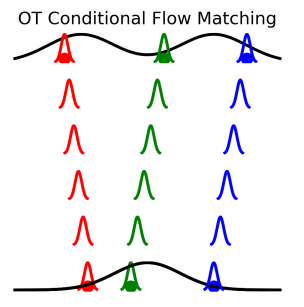
実際、下図のようにmoonから9つのガウス分布の生成を行っていますが、左側のI-CFMより、右側のOT-CFMが明らかにシンプルな遷移を行っています。

下図は、OT-CFMのアルゴリズムを示しています。

アルゴリズム中にOTのミニバッチ近似が出てきます。大きなデータセットにおいて、OTにおける輸送計画$\pi$の計算と保存は、困難な場合があり、OTのミニバッチ近似を使用するのが実用的です。実際、正確なOTの解に対して誤差が生じますが、多くのアプリケーションに適応可能になります。

実際アルゴリズムを見ると、変わったところは、OTの部分くらいかと思います。

Schrödinge Bridge CFM

論文中には、シュレディンガーBridge(SB)によるCFMもでてきます。勝手なイメージですが、I-CFMとOT-CFMの中間に当たると思っていますが、理論が複雑で説明が、かなり長くなりそうなので省きます。ぱっとみ、SB-CFMより、OT-CFMのほうが精度が良さそうでした。ただ、Schrodinger Bridges Beat Diffusion Models on Text-to-Speech Synthesisという論文もでていたので、次回の記事を書く際にしっかり理解したいと思います。（誰か書いてください！！）

ちなみにですが、Schrödinge Bridgeに関しては、以下の記事がとても参考になりました。すごく良い記事です！

• Morpho Tech log - A Brief Survey of Schrödinger Bridge (Part I)

比較

最後に比較結果です。
下図は、分布の適合度（一致度？）を示した2-Wasserstein $\mathcal{W}^2_2$と、最適輸送性能(Normalized Path Energy)で最適輸送性能を比較したものです。値が小さいほど性能がよいです。OT-CFMは、$\mathcal{W}^2_2$もNPEも、良さそうです。

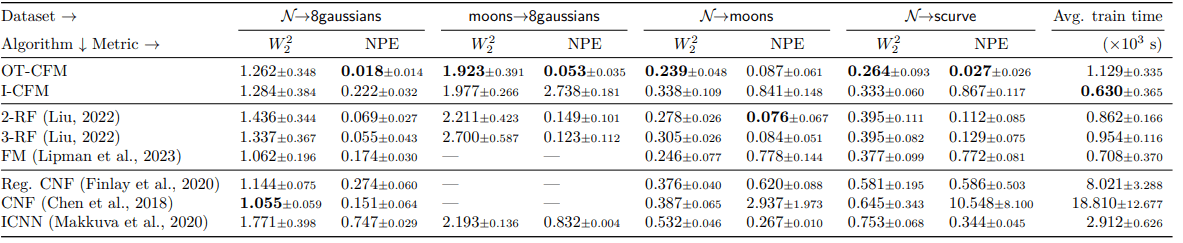
また、下図の左より、学習時の検証セットに対する誤差の収束も早いことがわかります。

プログラム上でどう記載するのか？

理論ばかり書いても、まぁわからないので、いくつか実装例を見てみましょう。

まずは、CFMを使用している音声合成モデルであるMatcha-TTSです。ここでは、$x_1$が目標となるデータで、エンコーダの出力であるメルスペクトログラム$mu$をflow matchingでいい感じに変換し$x_1$に近づけるため、$mu$という引数があります。

実装を見ると、概ねアルゴリズム通りですが、ランダムな$z$をサンプリングしておりI-CFNを実装しているという認識でよいのでしょうか。例えば、CNFは、分布の変換なので、入力のメルスペクトログラムの分布を正解のメルスペクトログラムの分布へ近づけるように実装しても良さそうな気がします。どうなんでしょうか？（ただ、他のCFMの実装の初期値も同様になっていました。）また、気になる点としては、確率経路の平均を計算する部分と、ベクトル場を計算する部分に、sigma_minが入っています。ただ、この値は、かなり小さい($1e^{-4}$)とかなので、無視しても良いかもしれませんが、実装上必要なのでしょうかね...　(他の実装では、$0.1$など割りと大きめの値が設定されている場合がありました。)

また、確率経路から、データ$x$をサンプルしていたはずですが、ここでは計算せず、直接ニューラルネットワークに入力しています。こちらも実装ならではなのかなという気がします。

https

def compute_loss(self, x1, mask, mu, spks=None, cond=None):
        """Computes diffusion loss

        Args:
            x1 (torch.Tensor): Target
                shape: (batch_size, n_feats, mel_timesteps)
            mask (torch.Tensor): target mask
                shape: (batch_size, 1, mel_timesteps)
            mu (torch.Tensor): output of encoder
                shape: (batch_size, n_feats, mel_timesteps)
            spks (torch.Tensor, optional): speaker embedding. Defaults to None.
                shape: (batch_size, spk_emb_dim)

        Returns:
            loss: conditional flow matching loss
            y: conditional flow
                shape: (batch_size, n_feats, mel_timesteps)
        """
        b, _, t = mu.shape

        # random timestep
        t = torch.rand([b, 1, 1], device=mu.device, dtype=mu.dtype)
        # sample noise p(x_0)
        x0 = torch.randn_like(x1)

        # 確率経路の平均計算
        y = (1 - (1 - self.sigma_min) * t) * x0 + t * x1
        
        # ベクトル場の計算
        u = x1 - (1 - self.sigma_min) * x0

        loss = F.mse_loss(self.estimator(y, mask, mu, t.squeeze(), spks), u, reduction="sum") / (
            torch.sum(mask) * u.shape[1]
        )
        return loss, y

これを、OT-CFMに改造してみましょう。実際動作させていないですが、おそらく以下のようになると思います。最適輸送には、POT: Python Optimal Transportというライブラリを使用します。

from functools import partial
import ot as pot

class OTCFM()
    def __init__(self, ot_method):
        if ot_method == "exact":
            self.ot_fn = pot.emd
        elif ot_method == "sinkhorn":
            self.ot_fn = partial(pot.sinkhorn, reg=reg)
        elif ot_method == "unbalanced":
            self.ot_fn = partial(pot.unbalanced.sinkhorn_knopp_unbalanced, reg=reg, reg_m=reg_m)
        elif ot_method == "partial":
            self.ot_fn = partial(pot.partial.entropic_partial_wasserstein, reg=reg)

    def get_map(self, x0, x1):
        """Compute the OT plan (wrt squared Euclidean cost) between a source and a target
        minibatch.

        Parameters
        ----------
        x0 : Tensor, shape (bs, *dim)
            represents the source minibatch
        x1 : Tensor, shape (bs, *dim)
            represents the source minibatch

        Returns
        -------
        p : numpy array, shape (bs, bs)
            represents the OT plan between minibatches
        """
        a, b = pot.unif(x0.shape[0]), pot.unif(x1.shape[0])
        if x0.dim() > 2:
            x0 = x0.reshape(x0.shape[0], -1)
        if x1.dim() > 2:
            x1 = x1.reshape(x1.shape[0], -1)
        x1 = x1.reshape(x1.shape[0], -1)
        M = torch.cdist(x0, x1) ** 2
        if self.normalize_cost:
            M = M / M.max()  # should not be normalized when using minibatches
        p = self.ot_fn(a, b, M.detach().cpu().numpy())
        return p
    def sample_map(self, pi, batch_size):
        r"""Draw source and target samples from pi  $(x,z) \sim \pi$

        Parameters
        ----------
        pi : numpy array, shape (bs, bs)
            represents the source minibatch
        batch_size : int
            represents the OT plan between minibatches

        Returns
        -------
        (i_s, i_j) : tuple of numpy arrays, shape (bs, bs)
            represents the indices of source and target data samples from $\pi$
        """
        p = pi.flatten()
        p = p / p.sum()
        choices = np.random.choice(pi.shape[0] * pi.shape[1], p=p, size=batch_size)
        return np.divmod(choices, pi.shape[1])

    def compute_loss(self, x1, mask, mu, spks=None, cond=None):
        """Computes diffusion loss

        Args:
            x1 (torch.Tensor): Target
                shape: (batch_size, n_feats, mel_timesteps)
            mask (torch.Tensor): target mask
                shape: (batch_size, 1, mel_timesteps)
            mu (torch.Tensor): output of encoder
                shape: (batch_size, n_feats, mel_timesteps)
            spks (torch.Tensor, optional): speaker embedding. Defaults to None.
                shape: (batch_size, spk_emb_dim)

        Returns:
            loss: conditional flow matching loss
            y: conditional flow
                shape: (batch_size, n_feats, mel_timesteps)
        """
        b, _, t = mu.shape

        # random timestep
        t = torch.rand([b, 1, 1], device=mu.device, dtype=mu.dtype)
        # sample noise p(x_0)
        x0 = torch.randn_like(x1)
        
        # OTを用いて、x0, x1をサンプル
        pi = self.get_map(x0, x1)
        i_arr, j_arr = self.sample_map(pi, x0.shape[0])
        x0, x1 = x0[i_arr], x1[j_arr]

        y = (1 - (1 - self.sigma_min) * t) * x0 + t * x1
        u = x1 - (1 - self.sigma_min) * x0

        loss = F.mse_loss(self.estimator(y, mask, mu, t.squeeze(), spks), u, reduction="sum") / (
            torch.sum(mask) * u.shape[1]
        )
        return loss, y

最後に

今回は、Flow Matchingをより効率的にした、OT-CFMについて解説しました。個人的に、数式が多く難しいな～と思いながらも、今後使える技術だと思い、記事にしてみました。この記事で、Flow Matchingの理解の手助けになればと思います。

今後は、シュレディンガーBridgeに関する記事か、実際にOT-CFMを使用した音声合成などの記事を作成できればと思っています。

---

最後に宣伝になりますが、機械学習でビジネスの成長を加速するために、Fusicの機械学習チームがお手伝いしています。機械学習のPoCから運用まで、すべての場面でサポートした実績があります。もし、困っている方がいましたら、ぜひFusicにご相談ください。お問い合わせから気軽にご連絡いただけますが、TwitterのDMからでも大歓迎です！

参考文献

• Normalizing Flow入門 第1回 変分推論
• Normalizing Flow入門 第2回 Planar Flow
• Normalizing Flow入門 第7回 Neural ODEとFFJORD