打倒!「モナドは単なる自己関手の圏におけるモノイド対象だよ。何か問題でも?」
モナドは単なる自己関手の圏におけるモノイド対象だよ。何か問題でも?
モナドについて調べているとたまに見かけるこの言葉をはじめて目にしたとき
「そっかー、モナドは単なる自己関手の圏におけるモノイド対象なのかー」と一旦は飲み込み「ところでモノイド対象って何?」とモノイド対象をググってトップに出てきたWikipediaの記事を見て

となり、そっ閉じしたことはありませんか?・・・・・・私はある。
わからなくてもモナド(プログラミング)は使えますしね。
というかプログラミング的にモナドを理解したいならモナドを実際使ったり書いたりした方がいいですしね。
しかし文章がなんか煽ってる風味なのもあって理解できないのは悔しかったので圏論の参考書を読んだり、Web検索したりして自分なりにまとめてきました。
それをせっかくなので、自分みたいな人に向けてアウトプットしようというのがこの記事になります。
この言葉の出典
この記事を読んだ方から、出典を書いた方がいいのではないかというフィードバックをもらったので、出典について加筆しました。
この言葉の出典は、James Iry氏の記事A Brief, Incomplete, and Mostly Wrong History of Programming Languages(不完全にしておよそ正しくないプログラミング言語小史 - 青木靖 訳)の次の箇所です。
1990 – サイモン・ペイトン・ジョーンズ、ポール・フダック、フィリップ・ワドラー、デミ・ムーアの夫、ならびに動物の倫理的扱いを求める人々によって構成される委員会により、遅延評価を行う純粋な関数型言語Haskellが作られる。副作用の制御に使われるモナドの複雑さのため、Haskellには抵抗を持つ人々がいる。ワドラーは批判を和らげるために、こう語っている。「モナドは単なる自己関手の圏におけるモノイド対象だよ。何か問題でも?」
(日本語訳から引用)
この文章ではWadler氏が語ったこととされていますが、そちらの出典はありません。
そもそもこの記事はタイトルに「およそ正しくない」と書かれていることから想像できるように、部分的に合っておりますが(上記でいうと、1990年はHaskell 1.0の誕生年なので、ここは合っている)、基本的にジョーク記事です。
そう考えると、やけに煽るような表現なのも納得できるのではないでしょうか。
ただ、モナドが自己関手の圏におけるモノイド対象なのはジョークではなく合っています。
また、ネットでは色々な意味で有名な言葉となっていますが、書籍『圏論の基礎(マックレーン)』ではモノイド圏とその中のモノイドの一例としてさらっと取り上げられているくらいの扱いだったりします。
なぜわかりそうでわからないのか。どうしたらいいのか。
一見簡単なことを言ってるようなのに、なぜよくわからないのかというと、これがくだけた表現を使ってるものの数学の言葉で端的に表されたものだからです。
「モナドはXXXだよ」ということを表現している短い文章に「自己関手の圏」「モノイド対象」といった概念が含まれているのですが、これら自体を説明するためには更に別の概念の理解が必要となっているため、気軽な気持ちで踏み込むと冒頭の私のように

となってしまうわけです。
例えば「モノイド対象」は「モノイド圏」という圏が与えられたときの(ある条件を満たす)対象として定義されるので、先にモノイド圏を知る必要があります。
更に「自己関手の圏における」という条件も加わります。
今書いたことを踏まえて絵で表してみましょう(単なる図です。圏論の図式ではないです)。
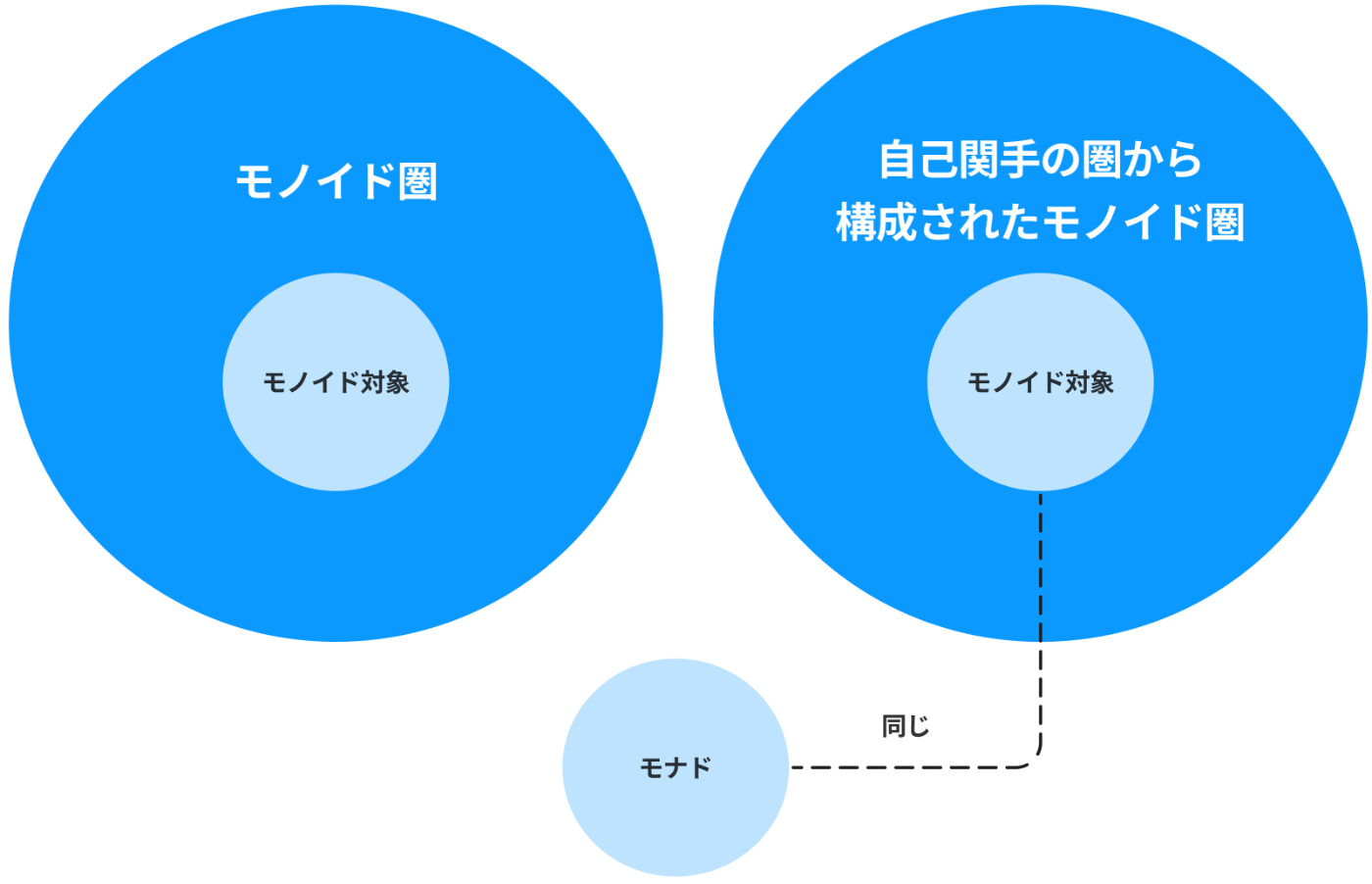
つまりモナドと同じだと言われている「自己関手の圏におけるモノイド対象」は圏に対してけっこー条件が加わったものになります。
このような場合は、満たすべき条件が少ないところから順々に理解していくとわかりやすいと思います。
それにあたってまず「モナドが自己関手の圏におけるモノイド対象である」ことの理解にはいったいどれだけ理解が必要な概念があるのか全体像をお見せしたいと思います。
ということで、文章を要素分解して、関連する概念を紐づけた図を用意しました。
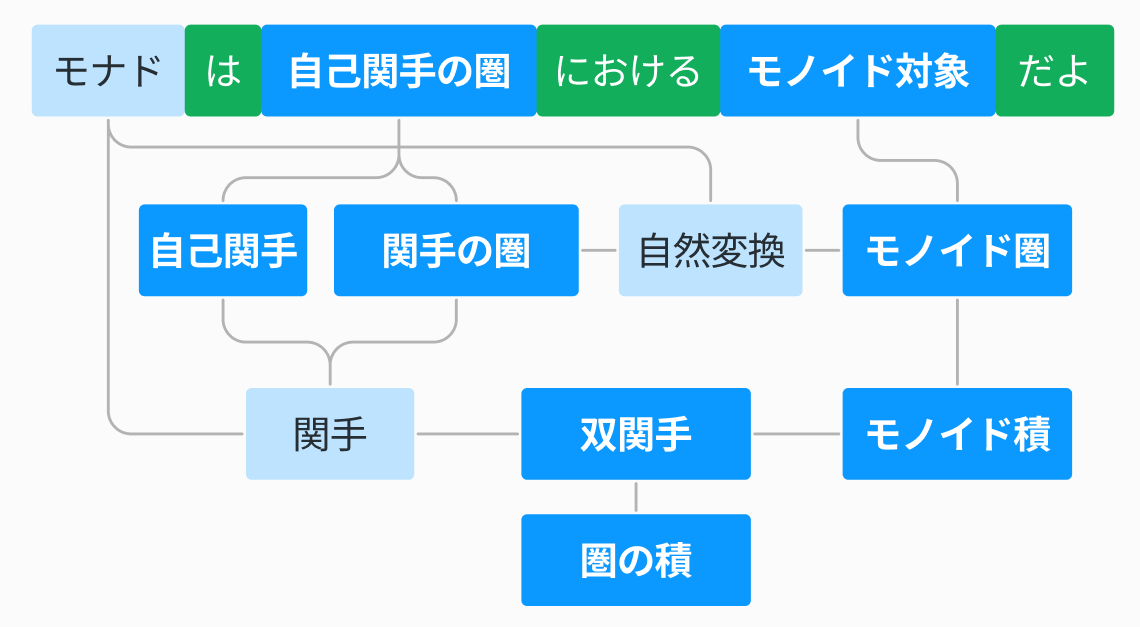
青色と水色の部分が関連する概念で、緑色はどうでもいい部分です。
水色の方は今回の記事の説明の対象外とした概念です。
これらのうち「モナド」「関手」「自然変換」の説明は他の良い記事があると思いますので、詳しい説明はそちらに譲ります。
(私も別の記事に書いています。)
ではこれから上記の概念を次の順に説明していきます。
- 自己関手
- 関手の圏
- 自己関手の圏
- 圏の積
- 双関手
- モノイド積
- モノイド圏
- モノイド対象
最終的にはモナドが自己関手の圏におけるモノイド対象だというところに繋がるでしょう。
自己関手の圏
まずは自己関手の圏を理解しましょう。
関連する概念はこちらです。

「自己関手」「関手の圏」「自己関手の圏」の順に見ていきましょう。
まずは自己関手です。
自己関手
自己関手とは、圏

次に関手の圏です。
関手の圏
二つの圏
この圏の恒等射は恒等自然変換であり、射の合成は自然変換の垂直合成になります。
これらにより圏の公理が満たされます。
図式を書いてみましょう。
例えば圏
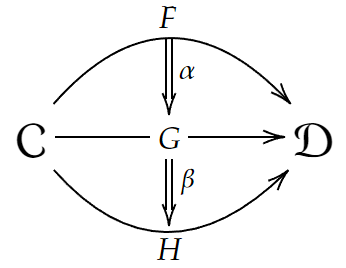
これをもとに関手圏

自己関手の圏
これは関手の圏がわかれば簡単で、関手の圏
モノイド対象
次はモノイド対象です。
関連する概念はこちらです。

モノイド対象はモノイド圏に対して定義されるのですが、そのモノイド圏を定義するにはモノイド積が必要となり、モノイド積は双関手の特別な場合なので、まず圏の積と双関手からはじめ、モノイド積、モノイド圏、モノイド対象、と進めようと思います。
圏の積
二つの圏
二つの射の合成射
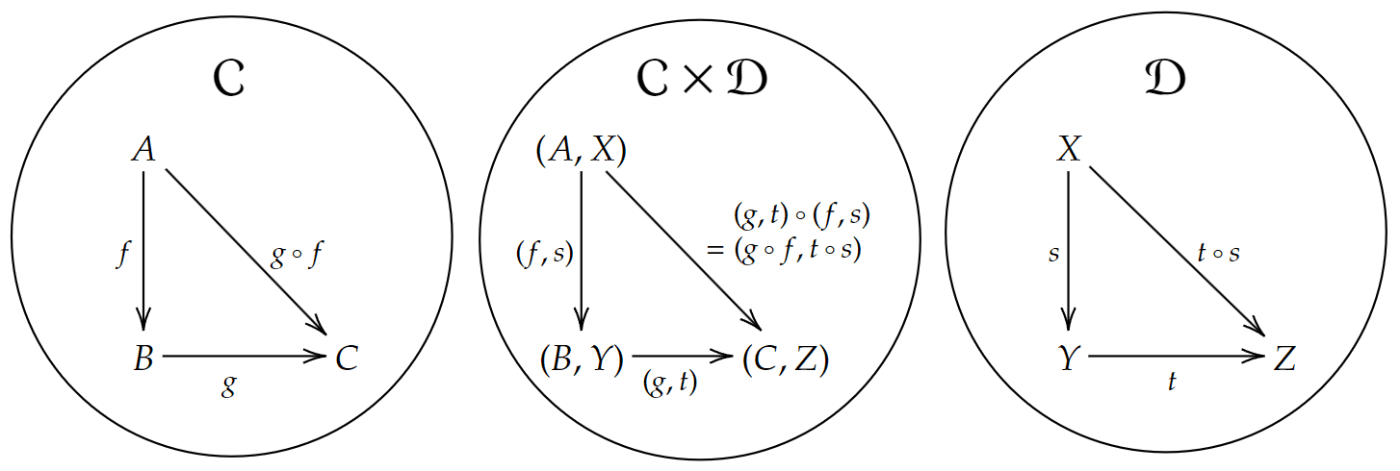
次は圏の積を用いて双関手を定義します。
双関手
圏
のことです。
したがって双関手
また
関手と同様に合成や恒等射も保存されます。
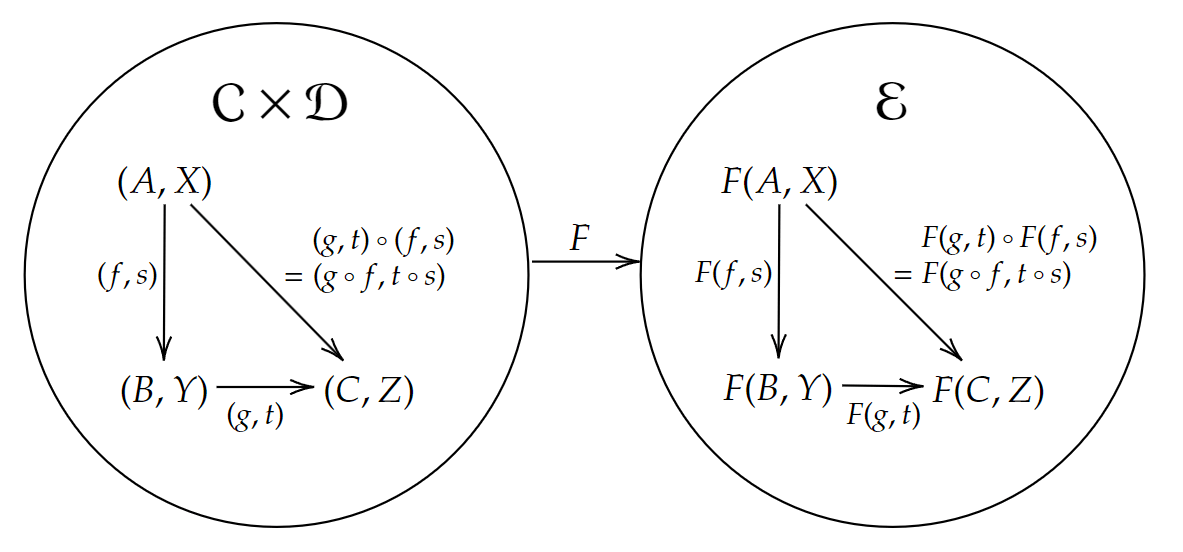
次は双関手を用いてモノイド積を定義します。
モノイド積
この後に定義を示そうとしているモノイド圏
をモノイド積(あるいはモノイダル積、テンソル積など)と呼びます。
一般的な双関手
圏の積および双関手のおさらいになりますが、
また
したがってモノイド積
また
合成の保存と恒等射の保存は次のようになります。
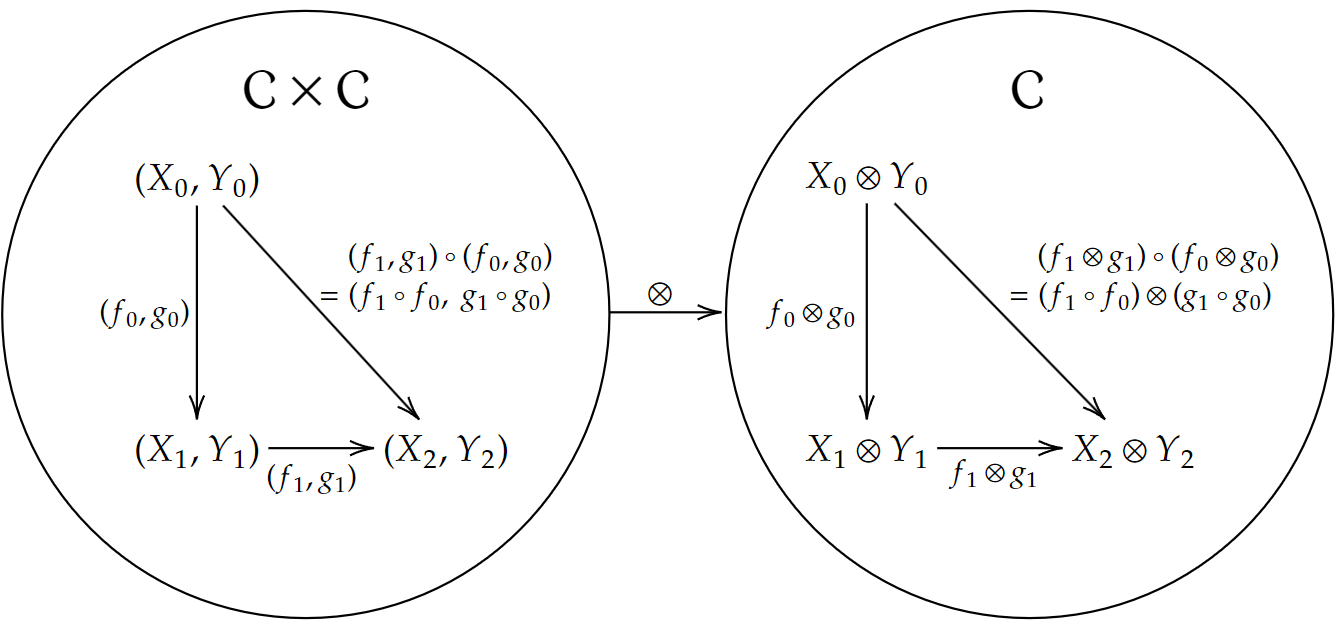
一般的な双関手が理解できていれば、難しくはなかったはずです。
これでモノイド圏の定義に必要な情報が揃ったので次はモノイド圏にいきます。
ここから情報量がいきなり増えます。
モノイド圏
モノイド圏(あるいはモノイダル圏)は、
- 圏
\footnotesize \mathcal{C} -
\footnotesize \mathcal{C} \footnotesize I - 双関手
\footnotesize \otimes:\mathcal{C}\times\mathcal{C}\rightarrow \mathcal{C} - 三つの自然同型
\footnotesize \alpha,l,r
からなる組
ここで単位対象
三つの自然同型
-
結合法則
\footnotesize \alpha
\footnotesize \mathcal{C} \footnotesize A,B,C \footnotesize \alpha _{A,B,C} :( A\otimes B) \otimes C\cong A\otimes ( B\otimes C)
モノイド積はこの自然同型\footnotesize \alpha \footnotesize \alpha -
恒等則
\footnotesize \mathcal{C} \footnotesize A \footnotesize I -
左恒等則
\footnotesize l
\footnotesize l_{A}:I\otimes A\cong A -
右恒等則
\footnotesize r
\footnotesize r_{A}:A\otimes I\cong A
-
左恒等則
三つの自然同型

五角図式
αについての補足
-
\footnotesize \alpha _{A\otimes B,C,D}
これは\footnotesize \alpha _{A,B,C} \footnotesize A \footnotesize A\otimes B \footnotesize B \footnotesize C \footnotesize C \footnotesize D
\footnotesize (( A\otimes B) \otimes C) \otimes D\rightarrow ( A\otimes B) \otimes ( C\otimes D) -
\footnotesize \alpha _{A,B\otimes C,D}
これは\footnotesize \alpha _{A,B,C} \footnotesize B \footnotesize B\otimes C \footnotesize C \footnotesize D
まず\footnotesize C \footnotesize ( A\otimes B) \otimes D\rightarrow A\otimes ( B\otimes D)
次にこれの\footnotesize B \footnotesize ( A\otimes ( B\otimes C)) \otimes D\rightarrow A\otimes (( B\otimes C) \otimes D) -
\footnotesize \alpha _{A,B,C\otimes D}
これも上記と同様に\footnotesize C \footnotesize C\otimes D
\footnotesize ( W\otimes X) \otimes ( Y\otimes Z)\rightarrow W\otimes ( X\otimes ( Y\otimes Z))
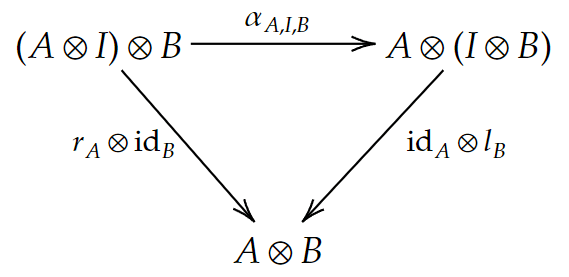
三角図式
さぁモノイド圏が終わり、いよいよモノイド対象までやってきました。
モノイド対象
モノイド対象とは、モノイド圏
-
圏
\footnotesize \mathcal{C} \footnotesize M -
乗法
\footnotesize \mu \footnotesize \eta -
\footnotesize \mu :M\otimes M\rightarrow M -
\footnotesize \eta :I\rightarrow M
の組
射
つまりモノイド圏の対象で、条件を満たす
二つの射
(
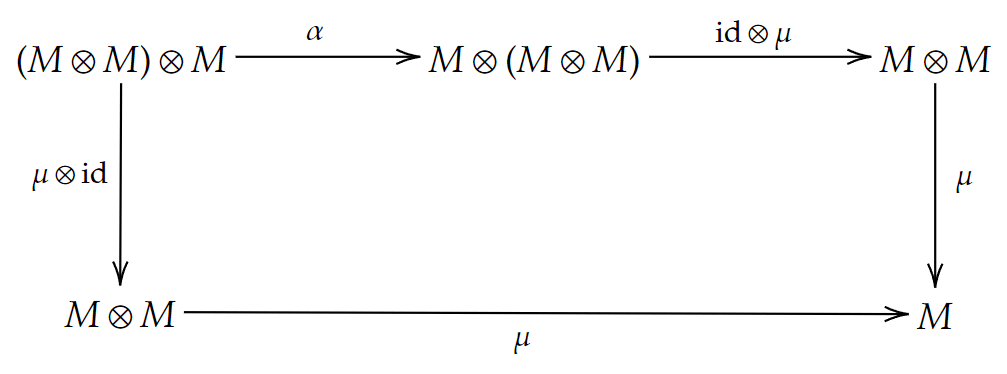
五角図式
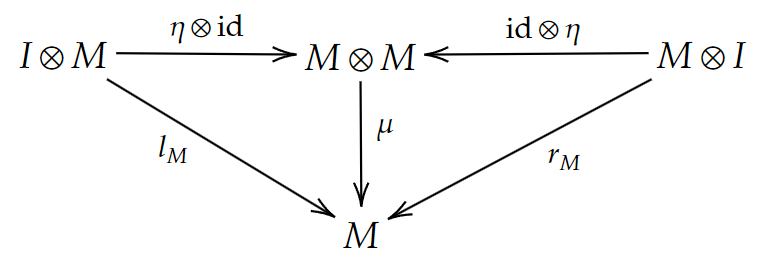
単位子図式
モノイド対象とモノイドの関係
圏論におけるモノイドとは、ただ一つの対象
つまりモノイドのあらゆる射のdomainとcodomainはどちらも
任意の圏
また詳しくは述べませんが、モノイド対象は定義を見るとモノイドと同じ性質を持っていることがわかります。
そうするとモノイド対象とは、モノイド圏の対象のうちモノイドとみなせる対象だということになりますね。
モノイドのプログラミング的な具体例を挙げてみると、例えば対象を文字列型とし、二項演算を文字列の結合、単位対象を空文字とした組はモノイドになっています。
実際いかなる文字列を結合したとしても結果は文字列型になりますし、空文字との結合は元の文字列を保ちます。
配列も二項演算を配列の結合とし、単位対象を空配列とすればモノイドになりますね。
具体的なコード例
具体的なコードとしてプログラミング言語としてPureScriptのモノイドの定義を見てみましょう。
(見やすくするために、一つにまとめてますが本当のコードはSemigroupとMonoidで分かれてます。またコメントを記入しています。)
-- 半群
class Semigroup a where
append :: a -> a -> a -- 結合的な二項演算
-- モノイド
class Semigroup m <= Monoid m where
mempty :: m -- 単位対象を返す
instance semigroupString :: Semigroup String where
append = concatString -- 文字列の結合
instance monoidString :: Monoid String where
mempty = "" -- 空文字
instance semigroupArray :: Semigroup (Array a) where
append = concatArray -- 配列の結合
instance monoidArray :: Monoid (Array a) where
mempty = [] -- 空配列
モノイドの例を載せましたが、半群が出てくるあたり圏論というより代数的構造よりの定義に感じました。
これでやっとモノイド対象まで終わりました。

すべての準備が整ったので、いよいよモナドが自己関手の圏におけるモノイド対象であることを見ていきます。
「モナドは自己関手の圏におけるモノイド対象だよ」とは
自己関手の圏におけるモノイド対象とは
まず自己関手の圏を用いてモノイド圏を構成できるということを見ていきます。
モノイド圏
- 圏
\footnotesize \mathcal{C} \footnotesize \mathcal{C^\mathcal{C}} - モノイド積
\footnotesize \otimes - 単位対象
\footnotesize I \footnotesize \mathrm{id}_\mathcal{C}
とした
すなわちこの圏の対象は自己関手になり、射は自然変換になります。
三つの自然同型
-
\footnotesize \alpha _{A,B,C} :( A\otimes B) \otimes C\cong A\otimes ( B\otimes C) \footnotesize \otimes \footnotesize l_{A}:\mathrm{id}_\mathcal{C} \otimes A\cong A \footnotesize r_{A}:A\otimes \mathrm{id}_\mathcal{C} \cong A
これは五角図式と三角図式を可換にします。

この圏におけるモノイド対象は
- 圏
\footnotesize \mathcal{C^\mathcal{C}} \footnotesize M - 自然変換
\footnotesize \mu :M\otimes M\rightarrow M \footnotesize \otimes - 自然変換
\footnotesize \eta :\mathrm{id}_\mathcal{C}\rightarrow M
からなる組
これで自己関手の圏におけるモノイド対象がわかりました。
自己関手の圏におけるモノイド対象とモナドを比較する
ここでモナドの定義を見てみます。
- 自己関手
{\footnotesize M} - 自然変換
{\footnotesize \mu :M\circ M\rightarrow M} - 自然変換
{\footnotesize \eta :\mathrm{id}_{\mathcal{C}}\rightarrow M}
からなる組
モナドもモノイド対象が定める二つの射
これにて「モナドが自己関手の圏におけるモノイド対象」であることがわかりました。
最後にそれぞれの図式を比較してみましょう。
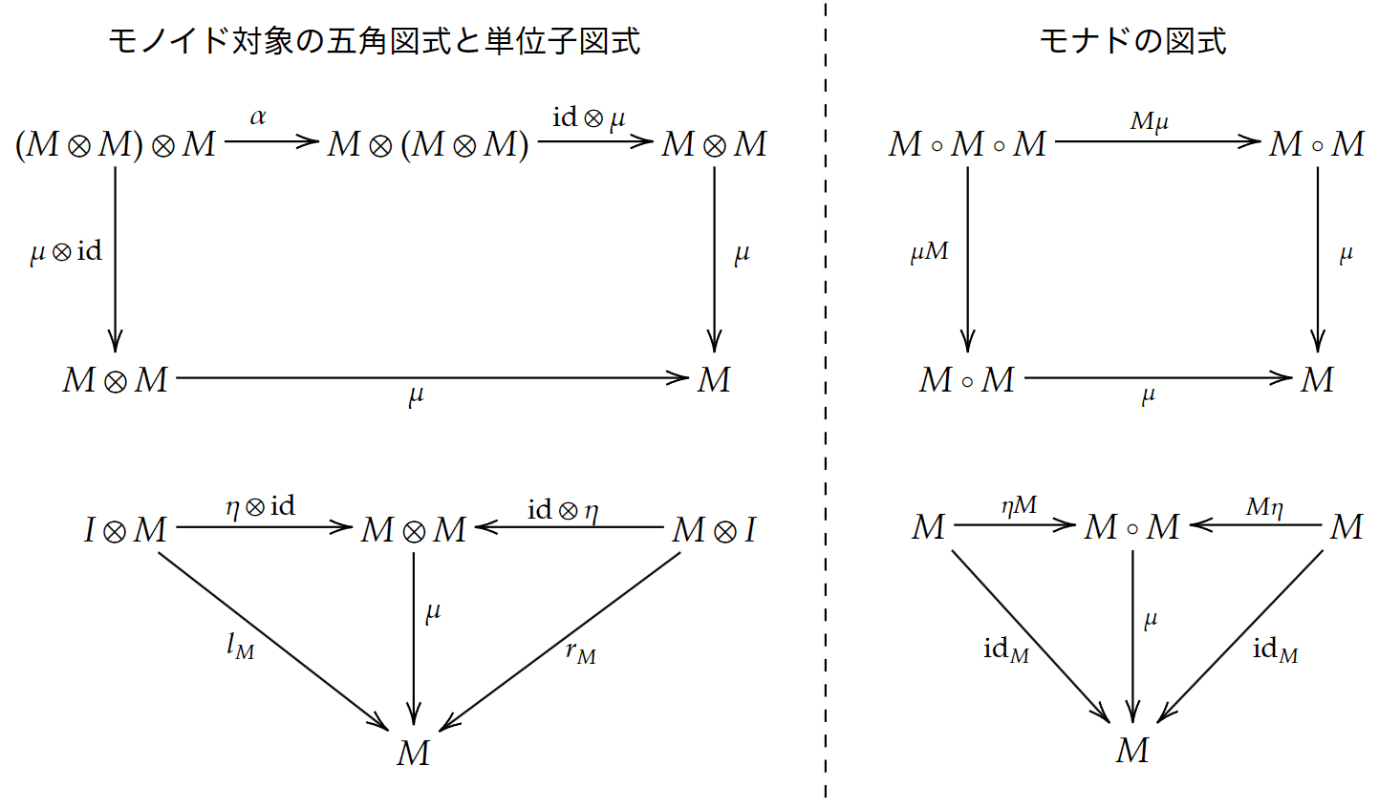
モノイド対象の方に結合法則が必要なことと、単位対象が含まれていることを除くと、かなり似た図式になっていますね。
参考資料
-
圏論の基礎 - マックレーン
大体この本に載ってます。 - ベーシック圏論 - レンスター
Discussion
丁寧な記事ありがとうございます!細かいですけど関手圏 [C, D] の別表記は C^D ではなくて D^C ですね 自己関手だと関係無いですが……
コメントありがとうございます!
見返したら誤っておりましたので表記を修正しました(感謝)。
図式は後ほど修正しようと思います(済)。