📝

拡散モデルと表データ生成②：【論文】CoDi

2024/03/16に公開

機械学習

CoDi: Co-evolving Contrastive Diffusion Models for Mixed-type Tabular Synthesis (ICML2023)

TabDDPMに続いてCoDiの論文を読んだので, そのまとめになります. まとめと言いつつかなり長くなっています. 図や表は断りのない限り論文からの引用です. arXiv版とPMLR版は同じように見えます.

arXiv
https://arxiv.org/abs/2304.12654

PMLR

書籍情報

Lee, C., Kim, J., and Park, N. CoDi: Co-evolving contrastive diffusion models for mixed-type tabular synthesis. In Krause, A., Brunskill, E., Cho, K., Engelhardt, B., Sabato, S., and Scarlett, J. (eds.), Proceedings of the 40th International Conference on Machine Learning, volume 202 of Proceedings of Machine Learning Research, pp. 18940–18956. PMLR, 23–29 Jul 2023.

TL;DR

数値データとカテゴリデータを別々に訓練する手法CoDiの提案
2つのモデルの橋渡しをするために互いに条件付けを行うco-evolving conditional diffusion modelsを設計
対照学習の手法を用いてより強固な橋渡しを実現 (負例はレコードをシャッフルして作成)
generative learning trilemmaの観点 (speed, quality, diversity)でバランスの良い結果

提案手法

論文のFigure 2がわかりやすい図になっています.

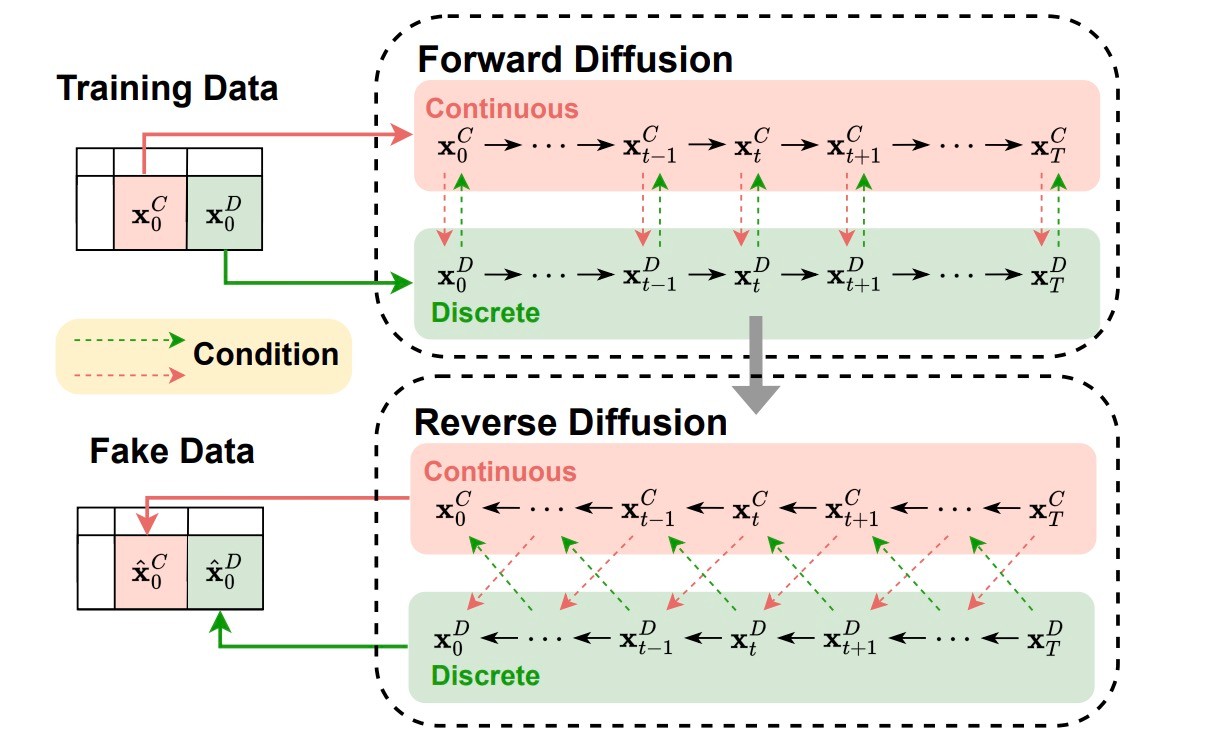
数値データは数値データでモデリングし, カテゴリデータはカテゴリデータでモデリングする手法になっています. TabDDPMと考え方は似ていて数値データに対してはGaussian Diffusion, カテゴリデータに対してはMultinomial Diffusionを用います. モデル設計で大きく違うのはTabDDPMでは単一のMLPでモデリングしていたのに対してCoDiでは別々のモデルをU-Netベースのアーキテクチャでモデリングする点にあります. 表データは分布はさることながら, 各レコードの横のつながりもあることが難しい点です. 提案手法では主に2つの手法を併用して解決を試みます.

Co-evolving Conditional Diffusion Models
Contrastive Learning

それぞれについて細かくみていきます.

Co-evolving Conditional Diffusion Models

一言で言えば, 互いの出力を互いの条件として入力することで横の繋がりを確保する手法です. ここでは欠損値のない入力 $\boldsymbol{x}_0$ を考えます. データは $N_C$ 個の数値カラム $C=\{C_1,C_2,\ldots,C_{N_C}\}$ と $N_D$ 個のカテゴリカラム $D=\{D_1,D_2,\ldots,D_{N_D}\}$ からなるものと仮定します. すなわち $\boldsymbol{x}_0=(\boldsymbol{x}_0^C, \boldsymbol{x}_0^D)$ です.

先ほど述べたように, 2つのdiffusion modelsを用いて, それぞれの出力をそれぞれの条件とします. 定式化すると

\begin{align*} & L_{\mathrm{Diff}_C}(\theta_C)\coloneqq \mathbb{E}_{t, \boldsymbol{x}_0^C, \varepsilon} \left[\|\varepsilon-\varepsilon_{\theta_C}(\boldsymbol{x}_t^C, t\mid\boldsymbol{x}_t^D)\|^2\right] \\ & L_{\mathrm{Diff}_D}(\theta_D)=\mathbb{E}_q\left[D_{\mathrm{KL}}[q(\boldsymbol{x}_T^D\mid\boldsymbol{x}_0^D)\|p(\boldsymbol{x}_T^D)]-\log p_{\theta_D}(\boldsymbol{x}_0^D\mid\boldsymbol{x}_1^D, \boldsymbol{x}_1^C) +\sum_{t=2}^TD_{\mathrm{KL}}(q(\boldsymbol{x}_{t-1}^D\mid\boldsymbol{x}_t^D,\boldsymbol{x}_0^D)\|p_{\theta_D}(\boldsymbol{x}_{t-1}^D\mid\boldsymbol{x}_t^D,\boldsymbol{x}_t^C))\right] \end{align*}

となります. この数式はほとんどDDPMと同じですので, 特に述べる点はありません. 以上がforward processの話です.

続いて, reverse processの話に移ります. ここでは時刻 $t$ の入力に時刻 $t-1$ の予測結果を用います. ここで, 以下の命題が成り立ちます.

Proposition 3.1

2つのforward processは以下の式で定義できる.

q(\boldsymbol{x}_t^C\mid\boldsymbol{x}_0^C)=\mathcal{N}(\boldsymbol{x}_t^C; \sqrt{\overline{\alpha}_t}\boldsymbol{x}_0^C, (1-\overline{\alpha}_t)\boldsymbol{I}) \\ q(\boldsymbol{x}_t^{D_i}\mid\boldsymbol{x}_0^{D_i})=\mathcal{C}(\boldsymbol{x}_t^{D_i};\overline{\alpha}_t\boldsymbol{x}_0^{D_i}+(1-\overline{\alpha}_t)/K_i)

ここで, $1\leq i\leq N_D, \alpha_t\coloneqq 1-\beta_t, \overline{\alpha}_t\coloneqq\prod_{i=1}^t\alpha_i$ である.

また, co-evolving conditional diffusion modelsのreverse processは以下のように定義できる.

\begin{align*} & p_{\theta_C}(\boldsymbol{x}_{0:T}^C)\coloneqq p(\boldsymbol{x}_T^C)\prod_{t=1}^Tp_{\theta_C}(\boldsymbol{x}_{t-1}^C\mid \boldsymbol{x}_t^C, \boldsymbol{x}_t^D) \\ & p_{\theta_D}(\boldsymbol{x}_{0:T}^{D_i})\coloneqq p(\boldsymbol{x}_T^{D_i})\prod_{t=1}^Tp_{\theta_D}(\boldsymbol{x}_{t-1}^{D_i}\mid \boldsymbol{x}_t^{D_i}, \boldsymbol{x}_t^C) \end{align*}

ここで, $1\leq i\leq N_D$ である.

Contrastive Learning

Co-evolving Conditional Diffusion Modelsだけでも数値データとカテゴリデータの繋がりはできますが, それをさらに強化するためにtriplet lossを用いた対照学習を導入します. 目的関数は以下のようになります.

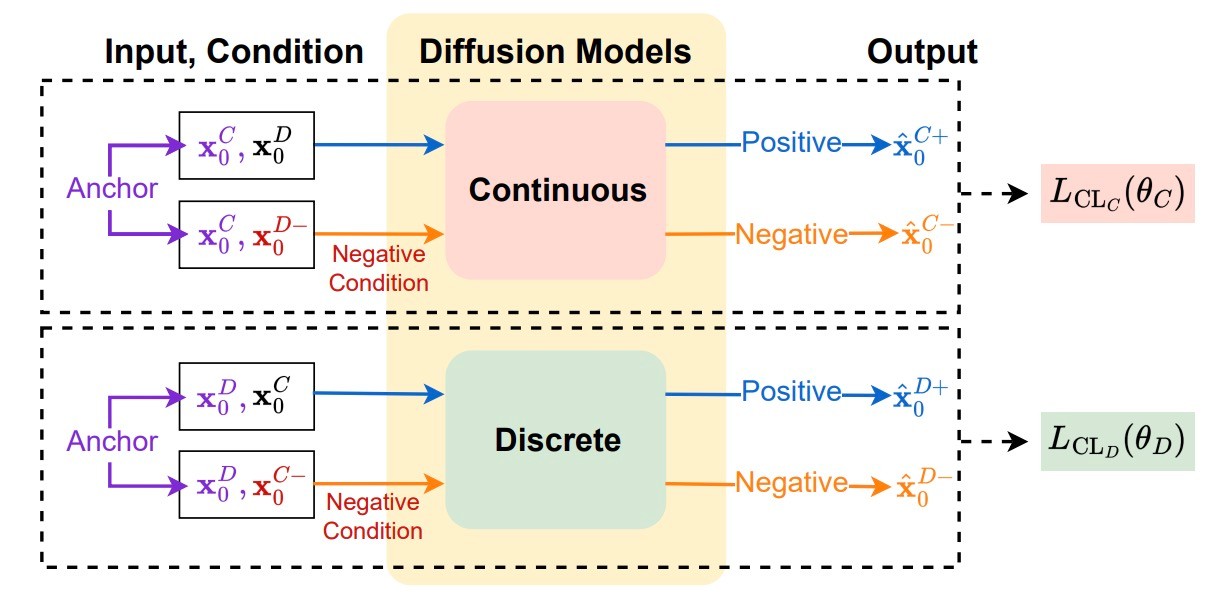
L_{\mathrm{CL}}(A, P, N)=\sum_{i=0}^S[\max\{d(A_i, P_i)-d(A_i, N_i)+m, 0\}]

$A$ がAnchor, $P$ がPositive Sample, $N$ がNegative Sample, $d$ は距離で $m$ はマージンです. $S$ はサンプル数です.

ここでも数値データとカテゴリデータを分けてlossを計算します. 実際のサンプル $\boldsymbol{x}_{0}^C$ をアンカーとし, $\boldsymbol{x}_{0}^D$ に条件付けられた生成されたサンプル $\hat{\boldsymbol{x}}_{0}^{C+}$ を正例とします. 負例には, $\boldsymbol{x}_{0}^{C}$ に対して不適切な負の条件 $\boldsymbol{x}_{0}^{D-}$ で生成された $\hat{\boldsymbol{x}}_{0}^{C-}$ を使用します。
拡散モデルは生成に時間がかかる傾向があり, 正例負例を用意するのは大変です. そのため, ここでは以下の式を用いて推定します.

\begin{align*} &\hat{\boldsymbol{x}}_{0}^{C+}=(\boldsymbol{x}_t^C-\sqrt{1-\overline{\alpha}_t}\varepsilon_{\theta_C}(\boldsymbol{x}_t^C,t\mid\boldsymbol{x}_t^D))/\sqrt{\overline{\alpha}_t} \\ &\hat{\boldsymbol{x}}_{0}^{C-}=(\boldsymbol{x}_t^C-\sqrt{1-\overline{\alpha}_t}\varepsilon_{\theta_C}(\boldsymbol{x}_t^C,t\mid\boldsymbol{x}_t^{D-}))/\sqrt{\overline{\alpha}_t} \end{align*}

同様に, カテゴリデータについても正例負例を直接推定します. 生成したのちは先ほどの目的関数 $L_{\mathrm{CL}}(A, P, N)$ を計算します. 距離として数値データにはユークリッド距離を, カテゴリデータに対してはcross entropyを用います. 拡散モデルのlossと組み合わせると以下のようになります.

\begin{align*} & L_C(\theta_C)=L_{\mathrm{Diff}_C}(\theta_C)+\lambda_C L_{\mathrm{CL}_C}(\theta_C) \\ & L_D(\theta_D)=L_{\mathrm{Diff}_D}(\theta_D)+\lambda_D L_{\mathrm{CL}_D}(\theta_D) \end{align*}

$\lambda_C, \lambda_D$ はともに $(0, 1)$ の区間に属します.

負例の作り方

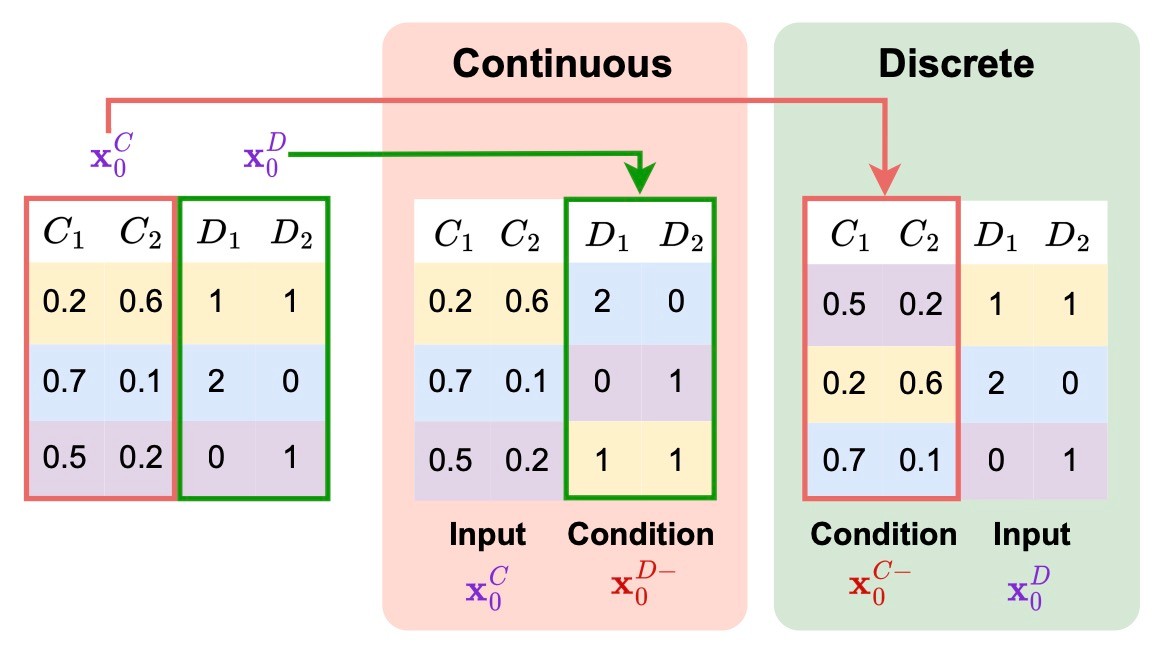
負例を作るためには負の条件 $\boldsymbol{x}_{0}^{C-}, \boldsymbol{x}_{0}^{D-}$ を定義しなければなりません. ここでは簡単に負の条件を作成します. それは, ランダムにシャッフルすることです. 次の図を見ると明快です. 元々正しく $C$ と $D$ の関係になっていた表に対して $C$ あるいは $D$ をランダムに並び替えます. すると正しい入力に対して誤った条件付けを行うことが可能になります. すなわち, 数値データとカテゴリデータの相関関係を破壊することで負の条件とします. ここで, 数値データの中のカラム同士の関係や, カテゴリデータの中のカラム同士の関係は維持します. 単純ですが, 後のAblation Studyで見るように, 効果的です.

アーキテクチャ

実験で性能を確認する前に, アーキテクチャの全体像を確認します. U-Netベースであることは触れました. 各Blockは全結合層で構成されています. 図が明瞭なのであえて数式で記述することはしません.

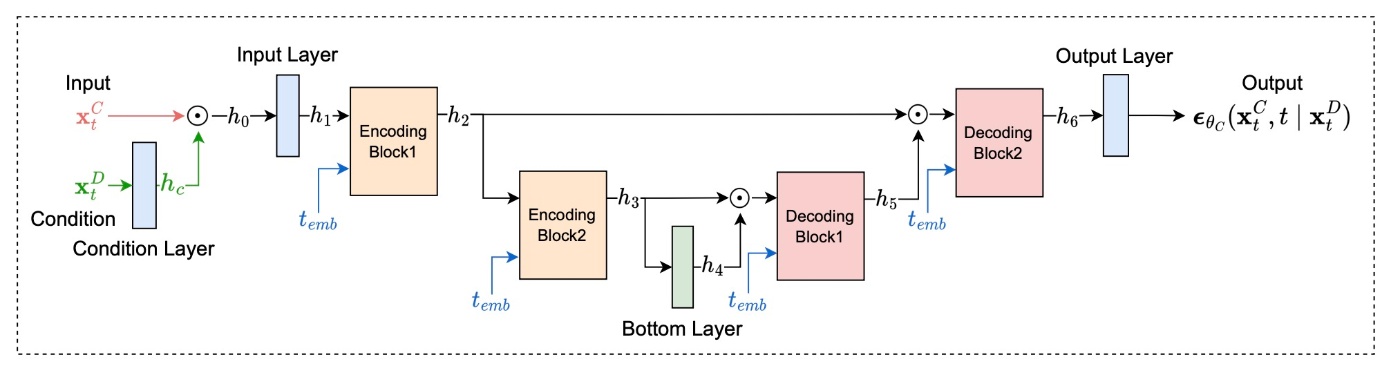
実験では, グリッドサーチで適切なハイパーパラメータを探索しているように見えます.

実験

8つのベースラインと11のデータセットを用います. データセットはmixed-typeなものを使用し, 前処理として数値データに対してはmin-max scalerを用いて $[-1,1]$ の範囲にします. カテゴリデータはone-hot encodingを施します.

generative learning trilemmaの観点から提案手法の評価を行います. これは生成データの品質, 多様性, スピードの観点で評価します. その結果, 採用された評価手法・指標は以下の3つです.

TSTR (Train on Synthesic, Test on Real): sampling qualityを測る方法です. 名前の通り, 生成データで分類器を訓練し, 実データでテストを行います. F1, AUROC ( $R^2$ RMSE)を評価指標として用います. まず5つの生成データからgrid searchでハイパーパラメータを選択します. その後, 5つの生成データで評価します.
coverage: sampling diversityを測る指標です. 値が大きいほどいい指標です.
wall-colck time: sampling speedを測る指標です. 10Kの生成を行う行うのに必要な時間を測定します. ここでも5回測定します.

Sampling Quality

全てのデータの平均の結果を示しています.

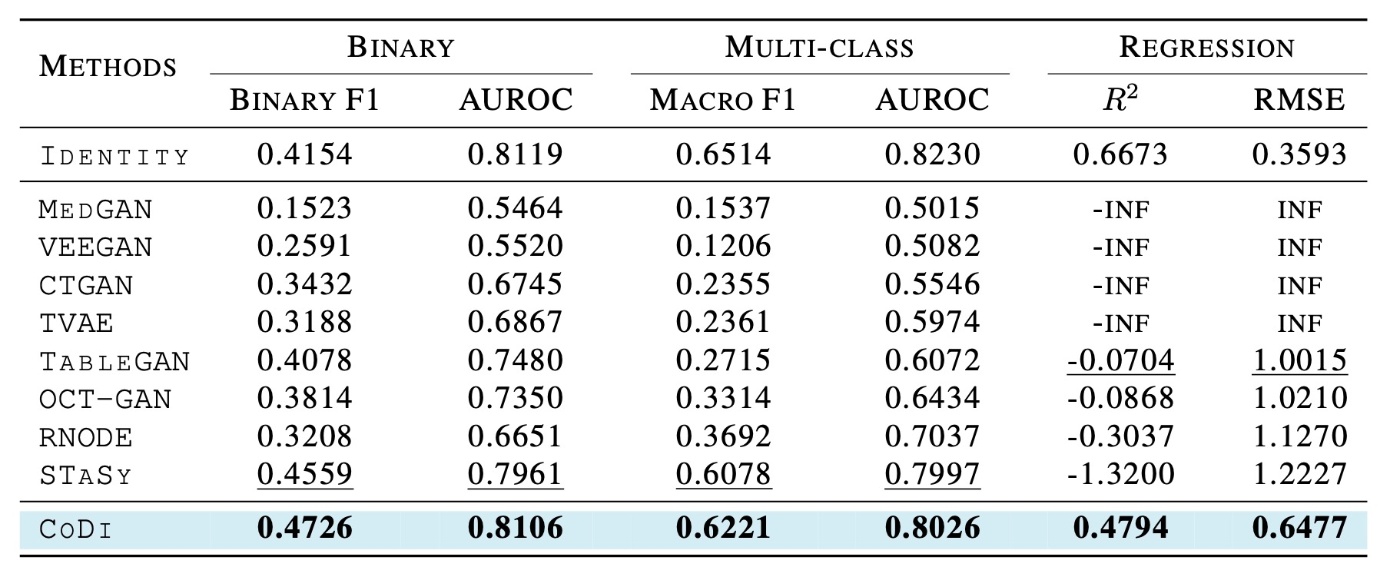
まず, 分類データの方を見てみます. Binary F1に着目するとMedGANとVEEGANは非常に品質が悪いです. Macro F1にも目を向けるとGANベースの手法は軒並み性能が低いことがわかります. 一方でスコアベースの手法であるSTaSyはかなり良い結果ですが, 提案手法には劣ります.

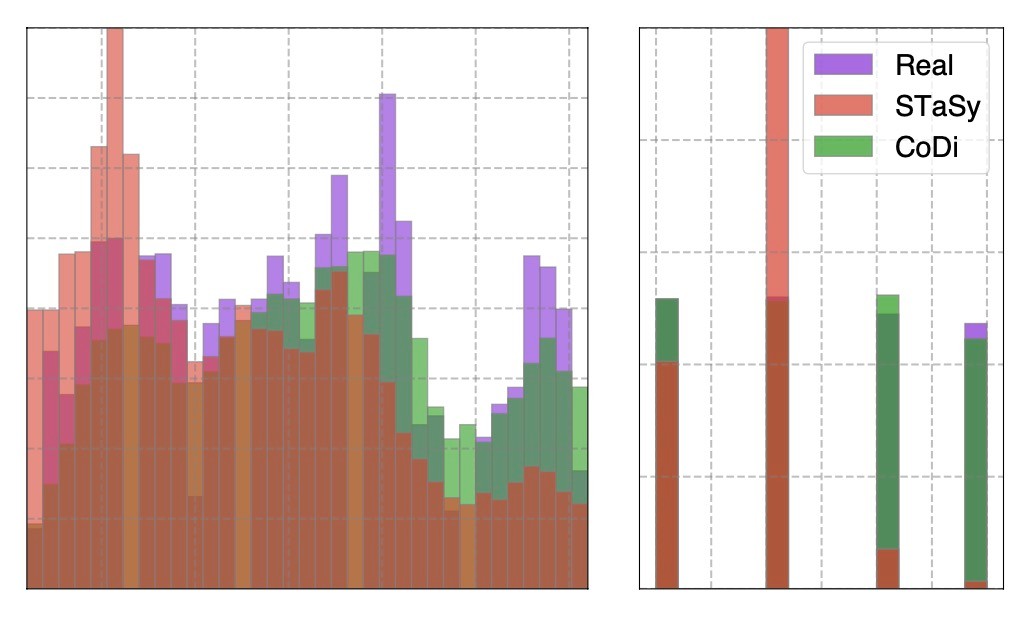
続いて, 回帰データを見てみます. 全てのベースラインの手法で $R^2$ が負になっているにもかかわらず, 提案手法は0.5に近い値で, 高品質な連続値生成も可能であることを示しています.

追加で, 分類データで同等の結果だったSTaSyを分布のヒストグラムで比較します. 左側がBankデータのDaysカラム (ここでは数値データとして扱われています), 右側がAbsentデータのSeasonsカラム (カテゴリデータ)になっています. これを見る限りではかなり分布に差があることがわかります. また, 提案手法であるCoDiの方が分布を模倣できているように見えます.　なお, 数値データをヒストグラムで表すのは適切でないと思います (今回は有限個しかないデータなのでヒストグラムで表せますが, それはカテゴリデータなのではないかと思います).

Sampling Diversity

続いて生成データの多様性を確認します. 先ほども述べたように, coverageという指標を使います. これは生成データに近い5つのデータの中に実データが含まれている生成データの割合です. 先ほどと同様に, 全データセットの平均のスコアを見てみます.

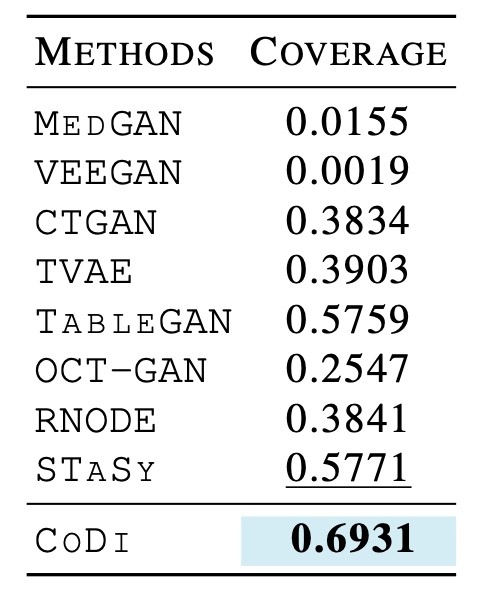
これを見ると, MedGANとVEEGANは多様性に欠ける生成結果であることがわかります. それ以外のベースラインはまずまずといった結果ですが, 提案手法は非常に優れた結果を示しています. 先ほどのsampling qualityもそうですが, データによってばらつきがある数値なのでまとめた結果をmain paperで示すのは不親切に見えます (Appendixでは個々のデータについての結果が示されています).

Sampling Speed

実行時間の結果を比較します. 生成数は10Kですが, 生成に用いるバッチサイズは記述されていません (おそらく生成数と同じです). GANベースの手法は非常に高速であることがわかりますが, Sampling Qualityの項で見た通り, 生成品質は良くありません. そのため, generative learning trilemmaを満たしているとは言い難いです.

Ablation Study

CoDiを構成する個々の要素のうち3つを検討しています.

カテゴリデータの扱い
負例の作り方
対照学習

順番に見たいと思います.

カテゴリデータの扱い

表データは混合データなので, 特にカテゴリデータが難しいです. 既存の, 特にGANベースの手法は潜在空間からデータ空間に射影するので, カテゴリデータを連続値として扱っています. 一方で本論文では離散空間で扱っています. その違いを検証するために, Car, Clave, Nursery, および Phishingデータを用いて実験します. これらのデータはカテゴリデータしか持たない表データになっています. そのため, 学習時における対照学習や条件付けは行なっていません.

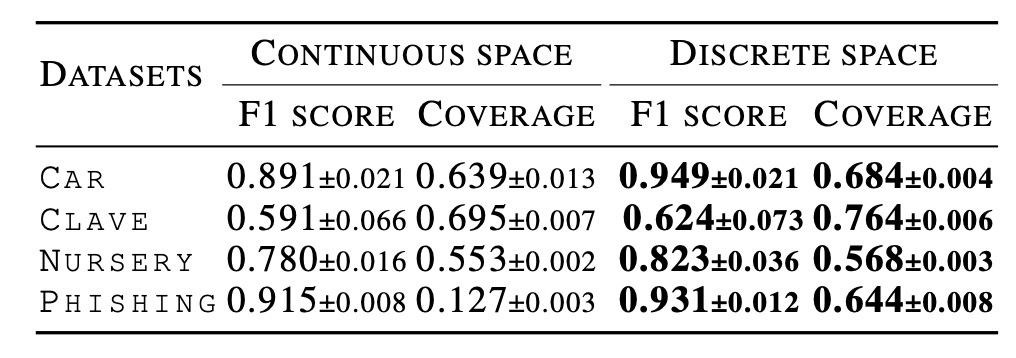
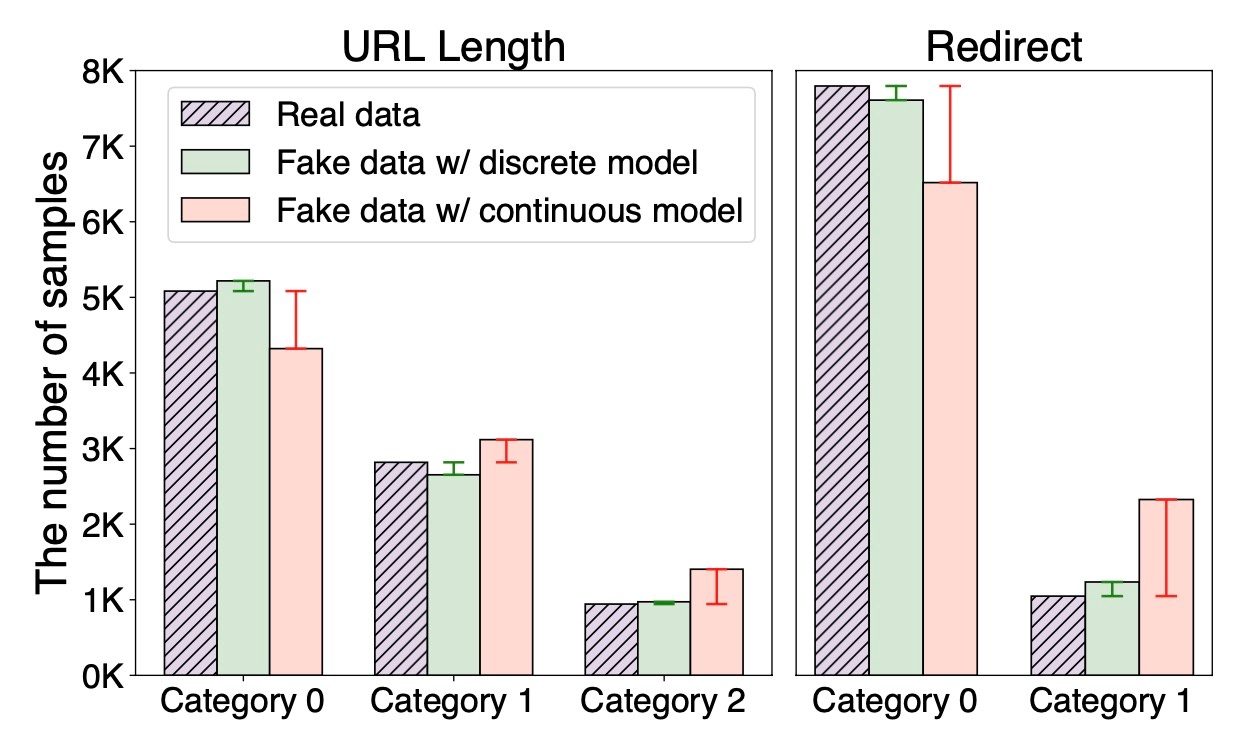
結果の表を見てみると, 一貫して離散空間で訓練した方がいいことがわかります. また, Phishingデータでの2つのカテゴリの分布を見てみます. これを見ると離散空間で訓練した方が実データとも分布が似ることがわかります. 個人的にはもっと多くのカテゴリを持つカラムを選定してほしいと思いました. また, 連続空間で処理する際の条件が不明瞭で正確な比較ではないように見えます. multinomial diffusionの場合は入力がone-hot encodingされていますが, 連続空間でもそうしているのでしょうか. 前処理は性能に直結しますので詳しく書いて欲しいです.

Negative Sampling Methods

生成品質と多様性の観点からnegative samplingの手法を比較します. CoDiではランダムシャッフルしていた部分に当たります. この論文では提案手法を含めた3つの方法で実験しています.

列を2つ選び, それらをランダムシャッフルする. その際に列の関係を保持する (下図では $(D_2, D_3)$ のペア).
列を2つ選び, それらをランダムシャッフルする. その際に列の関係は保持しない.

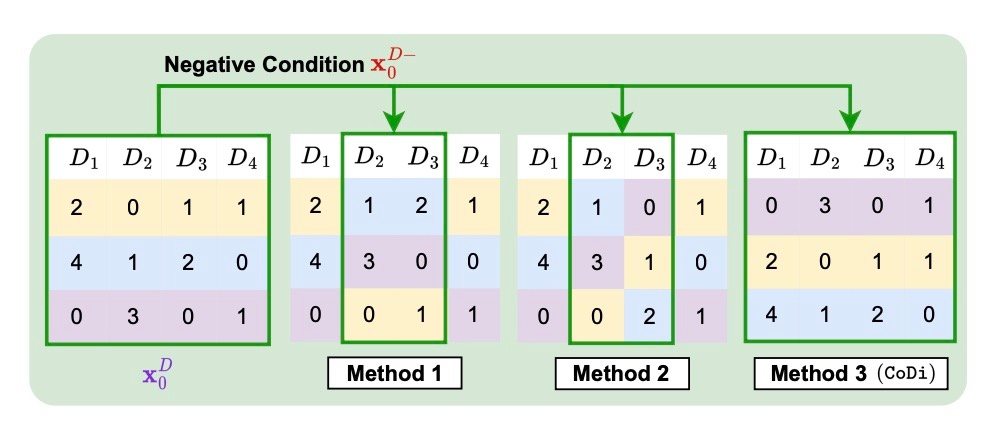
図ではカテゴリデータに対してのみ書かれていますが, 数値データの場合も同様です. 結果を見てみます.

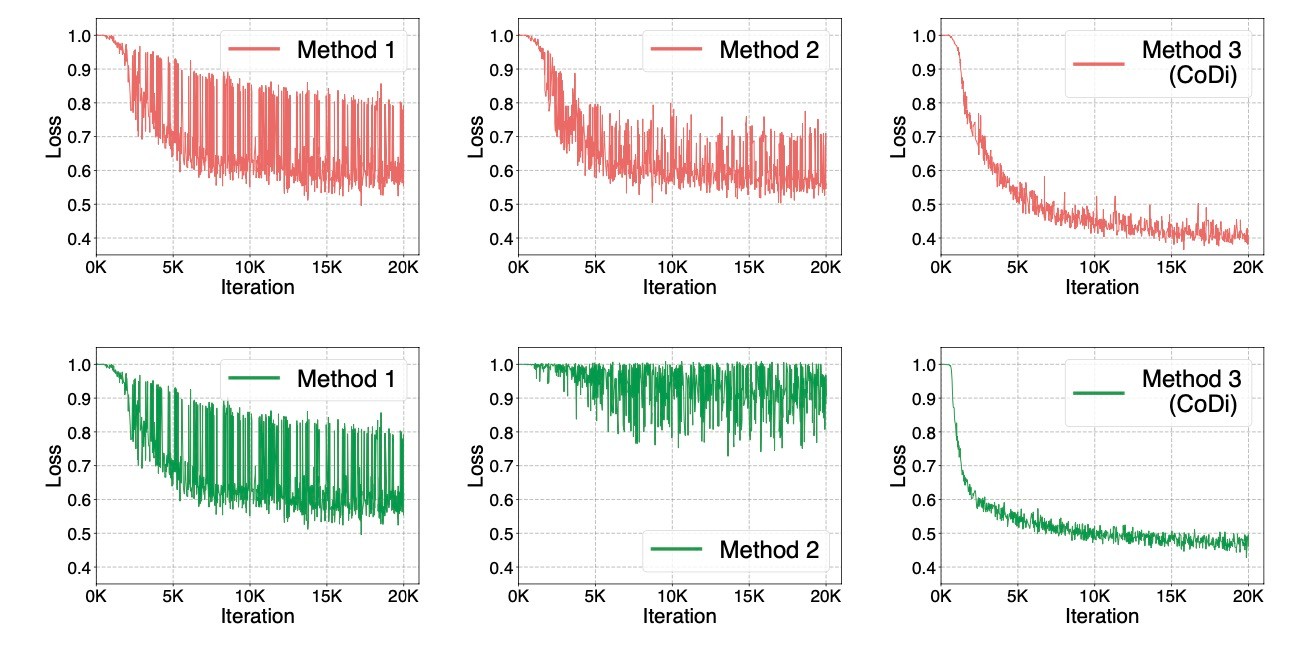
正直なところ, 生成品質が極めて向上したとは思いませんが, 多様性は大幅に向上しています. これは全てのカラムのペアを維持したままシャッフルすることが起因しています. Method1とMethod2はそれを破壊してしまうので訓練の難易度が上昇しています. 著者らはそれが結果に繋がったと考えているようです. 実際に, Faultsデータでの訓練時のtriplet lossのグラフをプロットしたものが下図になります. 上が数値データ, 下がカテゴリデータですが, どちらの場合もMethod3は安定してlossが下がっていることがわかります. 一方でMethod2は特にカテゴリデータのときは全然下がっていないことがわかります. Method1も2もlossの動きが大きく, 学習が安定しないことがわかります.

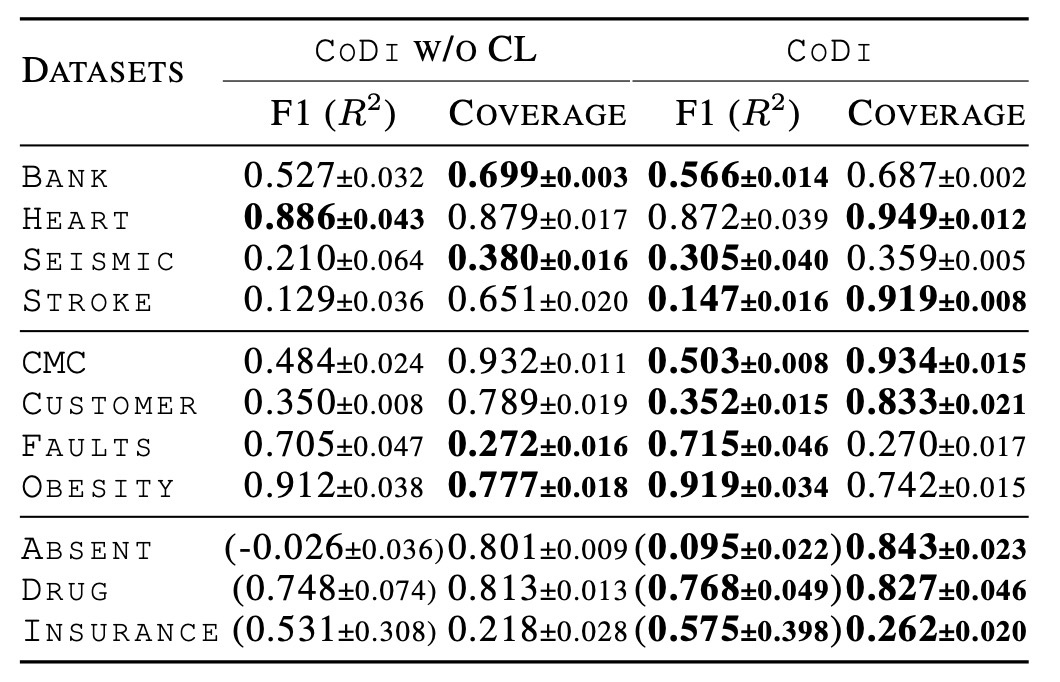
対照学習

ここでは通常のablation studyと同様に, 対照学習が必要かどうかを実験しています. 全体として右側の対照学習ありの方がスコアがいいことがわかります. 論文では具体的なデータ名を挙げて向上したと述べていますが, 上昇幅は小幅なものが多く, 対照学習で費やされる訓練時間に対するリターンはあまり大きくないように見えます. 一部スコアが下がっているものもありますが, それに対する考察等はありませんでした.

まとめ

数値データとカテゴリデータを別々に訓練することで分布をより良く学習する手法の提案
2つのモデルの橋渡しをするために互いに条件付けを行うco-evolving conditional diffusion modelsを設計. 対照学習の手法を用いてより強固な橋渡しを実現
generative learning trilemmaの観点 (quality, diversity, speed)でバランスの良い結果を達成

思ったこと

互いの出力を互いの条件にするのは直感的で, とても良いと思いました.
表データで対照学習するのは新しいなと思いました. 図もわかりやすくて理解しやすかったです.
論文のconclusionではSTaSyと比較して訓練難易度が減少したことによりsampling時間が90%削減されたと述べられていますが, 訓練と生成は別のフェーズなので不適切な気がします. また, generative learning trilemmaの観点にも訓練時間は入っておらず, 主張がやや変に見えます.
実行時間に関連して, 個々のデータで学習する必要がある表データ生成で訓練時間が考慮されていないのは疑問符がつきます. ある程度の品質低下を許容しても訓練が早く終わる方がいいという場面もあるはずです.
実験に用いたデータセットが全体的に小さく, 一番大きくても36kくらいです. もっと大きいデータはたくさんあるのでそれらでの実験が欲しいです.
U-Netを用いていますが, これのablationも欲しいです. arXivにはTabDDPMの約半年後に投稿されていたので比較がないのも含めて言及もないのは気になります.

参考文献

Lee, C., Kim, J., and Park, N. CoDi: Co-evolving contrastive diffusion models for mixed-type tabular synthesis. In Krause, A., Brunskill, E., Cho, K., Engelhardt, B., Sabato, S., and Scarlett, J. (eds.), Proceedings of the 40th International Conference on Machine Learning, volume 202 of Proceedings of Machine Learning Research, pp. 18940–18956. PMLR, 23–29 Jul 2023. (https://proceedings.mlr.press/v202/lee23i.html)