Zenn
👋

拡散モデルと表データ生成①：【論文】TabDDPM

2024/03/12に公開
機械学習
#
拡散モデル
#
表データ生成
tech

TabDDPM: Modeling Tabulr Data with Diffusion Models (ICML2023)

拡散モデルを用いて表データ生成を行うTabDDPMの論文を読んだのでその内容をまとめました. 論文のmain paperの部分をまとめています. 図や表はことわりがない限り, 論文からの引用です.

TabDDPMはarXiv版とICML版の2つがありますが, ICML版のまとめになります.

arXiv版

ICML版

書籍情報

Kotelnikov, A., Baranchuk, D., Rubachev, I., and Babenko, A. TabDDPM: Modelling tabular data with diffusion models. In Krause, A., Brunskill, E., Cho, K., Engel- hardt, B., Sabato, S., and Scarlett, J. (eds.), Proceedings of the 40th International Conference on Machine Learn- ing, volume 202 of Proceedings of Machine Learning Research, pp. 17564–17579. PMLR, 23–29 Jul 2023.

関連リンク

TL;DR

  • 拡散モデルで表データ生成を行う手法であるTabDDPMの提案. シンプルな設計で混合データ生成が可能
  • GANやVAEベースの手法より高性能な結果で, 昔ながらのSMOTEはGANやVAEを上回った
  • 同程度のパフォーマンスであるSMOTEと比較するとプライバシーの面で優れていることを確認

表データに対する生成モデル

この論文では表データ生成の特徴を挙げています.

  1. 表データはサイズが限られている. 昨今のLLMなどでは非常に大規模なデータをインターネットから収集しますが, そこには余分なデータが多くあります. 表データはそのような余分なデータが少ない傾向にあります. このことは品質を保つ上ではいいことですが, そもそもの数が少なすぎて深層学習に適さない場合もあります.
  2. 生成データは実際のユーザ情報を含まないので, 公開しやすい.
  3. よく知られた事実として, 表データはmixed typeなデータである.

提案手法: TabDDPM

表データには数値データ (numerical data)とカテゴリデータ (categorical data)と呼ばれる2つの種類のデータから構成されていることがほとんどです. 基本的にはこの特性が違う2つのデータをどのようにして扱うかが問題になります.

TabDDPMでは数値データをGaussian Diffusionでモデリングし, カテゴリデータはMultinomial Diffusionでモデリングします. 以降では, Gaussian Diffusionは前提としますので, 詳しくはDDPMの論文などをご覧ください.

Multinomial Diffusion

Multinomial Diffusionは主題ではないので簡単に触れる程度にします. 詳しくは論文の方を参照ください.

Multinomial Diffusion Modelsはカテゴリデータを生成するための設計をした拡散モデルです. まず, K クラスのカテゴリデータ x_t が与えられると考えます. カテゴリデータはone-hot encodingを施していて, x_t\in \{0, 1\}^K と表されます. Multinomial forward processでは q(x_t\mid x_{t-1}) を K クラスの一様ノイズによってデータを破損させるカテゴリ分布として定義します.

\begin{align*} & q(x_t\mid x_{t-1}) \coloneqq \mathrm{Cat}(x_t;(1-\beta_t)x_{t-1}+\beta_t/K) \\ & q(x_T) \coloneqq \mathrm{Cat}(x_T;1/K) \\ & q(x_t\mid x_0)=\mathrm{Cat}(x_t;\overline{\alpha}_tx_0+(1-\overline{\alpha}_t)/K) \end{align*}

この式から事後分布 q(x_{t-1}\mid x_{t},x_0) は以下のようになります.

q(x_{t-1}\mid x_{t},x_0)=\mathrm{Cat}\left( x_{t-1};\pi / \displaystyle\sum_{k=1}^K\pi_k \right)

ここで,

\pi=[\alpha_tx_t+(1-\alpha_t)/K] \odot [\overline{\alpha}_tx_0+(1-\overline{\alpha}_t)/K]

です. 逆分布 p_{\theta}(x_{t-1}\mid x_t) は \hat{x}_0 がNNによって予測される時に q(x_{t-1}\mid x_t, \hat{x}_0(x_t, t)) とパラメータ化されます. モデルはGaussian Diffusionと同様に変分下限を最大化するように学習します.

TabDDPM

さて, 提案手法に戻ります. 表データは混合データなので x=[x_{\mathrm{num}}, x_{\mathrm{cat_1}}, \ldots, x_{\mathrm{cat}_C}] と書けます. ここで, x_{\mathrm{num}} は数値データのカラム数 N_{\mathrm{num}} を用いて x_{\mathrm{num}}\in\mathbb{R}^{N_{\mathrm{num}}} の次元数を持っています. また, カテゴリデータはカラム数を C としたときに各カテゴリカラム x_{\mathrm{cat}_i} は K_i のカテゴリ値を持つとします. カテゴリデータはMultinomial Diffusionでモデリングするのでone-hot encodingを行います. これをモデルの入力とします. すなわち, モデルの入力次元は N_{\mathrm{num}}+\sum K_i です. モデルはDDPMに従って簡単化した損失 L_t^{\mathrm{simple}}=\mathbb{E}_{x_0,\varepsilon,t}\|\varepsilon-\varepsilon_{\theta}(x_t,t)\|_2^2 を使います. モデルの損失関数は

L_t^{\mathrm{TabDDPM}}=L_t^{\mathrm{simple}}+\dfrac{\sum_{i\leq C}L_t^i}{C}

です. 分類ラベルのあるデータにはラベルを条件として用います. 回帰データについては目的変数を数値データに含めて生成します.

モデルは簡単なMLPアーキテクチャを用います.

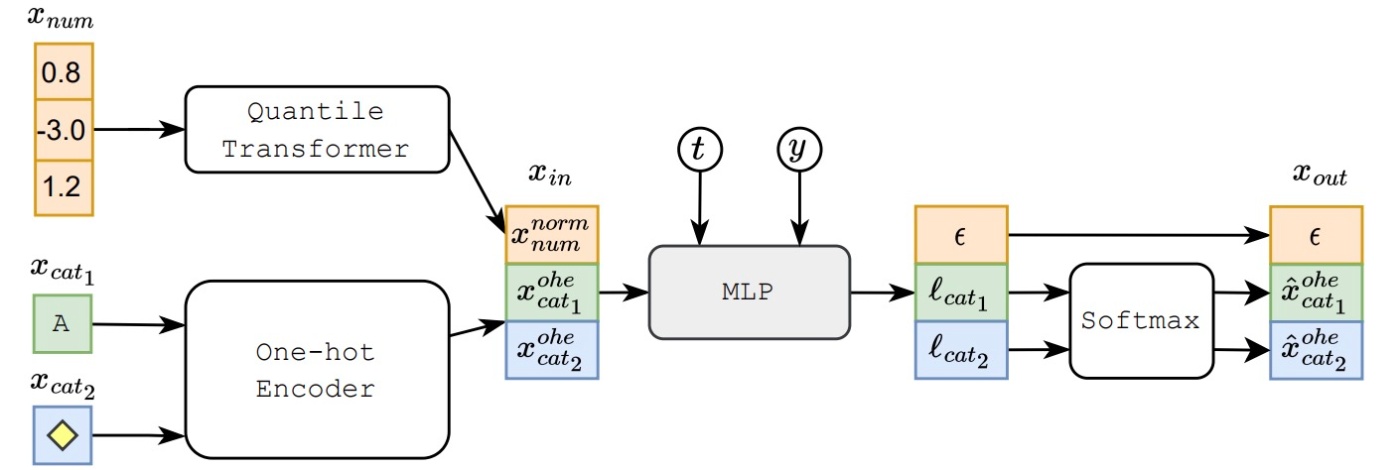
MLPの構造を式にすると

\begin{align*} &\texttt{MLP}(x)=\texttt{Linear}(\texttt{MLPBlock}(...(\texttt{MLPBlock}(x)))) \\ & \texttt{MLPBlock}(x) = \texttt{Dropout}(\texttt{ReLU}(\texttt{Linear}(x))) \end{align*}

です. MLP Blockをいくつ用意するかはハイパーパラメータで制御され, 後述の実験ではOptunaによって2, 4, 6, 8の範囲で最適化されます (MLPの出力の次元も同様に最適化されます). 時間情報やラベル情報を組み込んだものを入力 x とします.

\begin{align*} & t\_emb=\texttt{Linear}(\texttt{SiLU}(\texttt{Linear}(\texttt{SinTimeEmb}(t)))) \\ & y\_emb=\texttt{Embedding}(y) \\ & x=\texttt{Linear}(x_{in})+t\_emb+y\_emb \end{align*}

\texttt{SinTimeEmb} は次元が128の正弦波による埋め込みです.

ですが, 公式実装では以下のように y を埋め込んでいます.

y\_emb=\texttt{SiLU}(\texttt{Embedding}(y))

https://github.com/yandex-research/tab-ddpm/blob/main/tab_ddpm/modules.py#L458

ResNetを用いた実装も公式実装にはありますが, 論文では記述がありません.

実験結果

15の実データを用いて実験します. ベースラインを含めて全てハイパーパラメータ探索をOptunaを用いて行います. 論文では主に3つの観点から評価を行っています.

  1. 定性的評価
  2. Machine Learning Efficiency
  3. プライバシー

定性的評価

ここではTVAEとCTABGAN+をベースラインとして定性的な比較を行います. 表データ生成の定性的比較といえばカラム間の相関やカラムごとの値の分布を見ることになります. まず, 各データの特定のカラムについての分布を確認します.

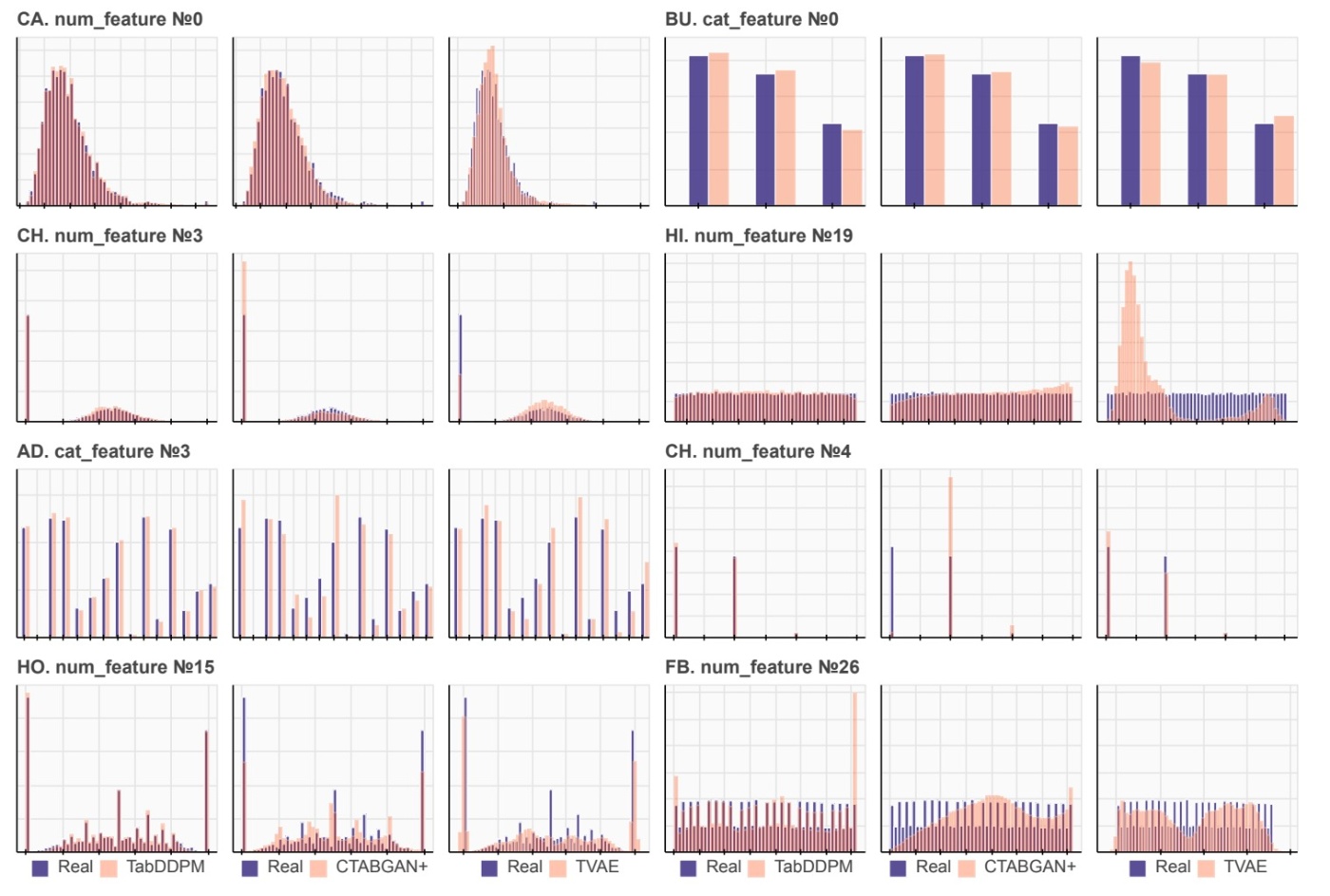
論文ではほとんどの場合でベースラインよりリアルな分布であると主張されています. HIやFBデータセットでの結果が非常にわかりやすいと思います. 数値データに着目するとTVAEはHI, FBなどの, 特に一様分布である場合に分布が訓練データと異なっていることがわかります. CTABGAN+はかなり分布を捉えられているものの, FBなどのカラム数が多いデータでは失敗してしまうことがわかります. カテゴリデータについても主張がなされているものの, 各カテゴリカラムのunique valueの数は多くないのでこれらの結果から何かを強く主張することは難しいように思えます.

続いて, カラム間の相関関係を見てみます. 数値カラム同士の相関にはピアソン相関を, カテゴリカラム同士の相関にはTheilのU統計量を, 数値カラムとカテゴリカラムの相関には相関比を用います.

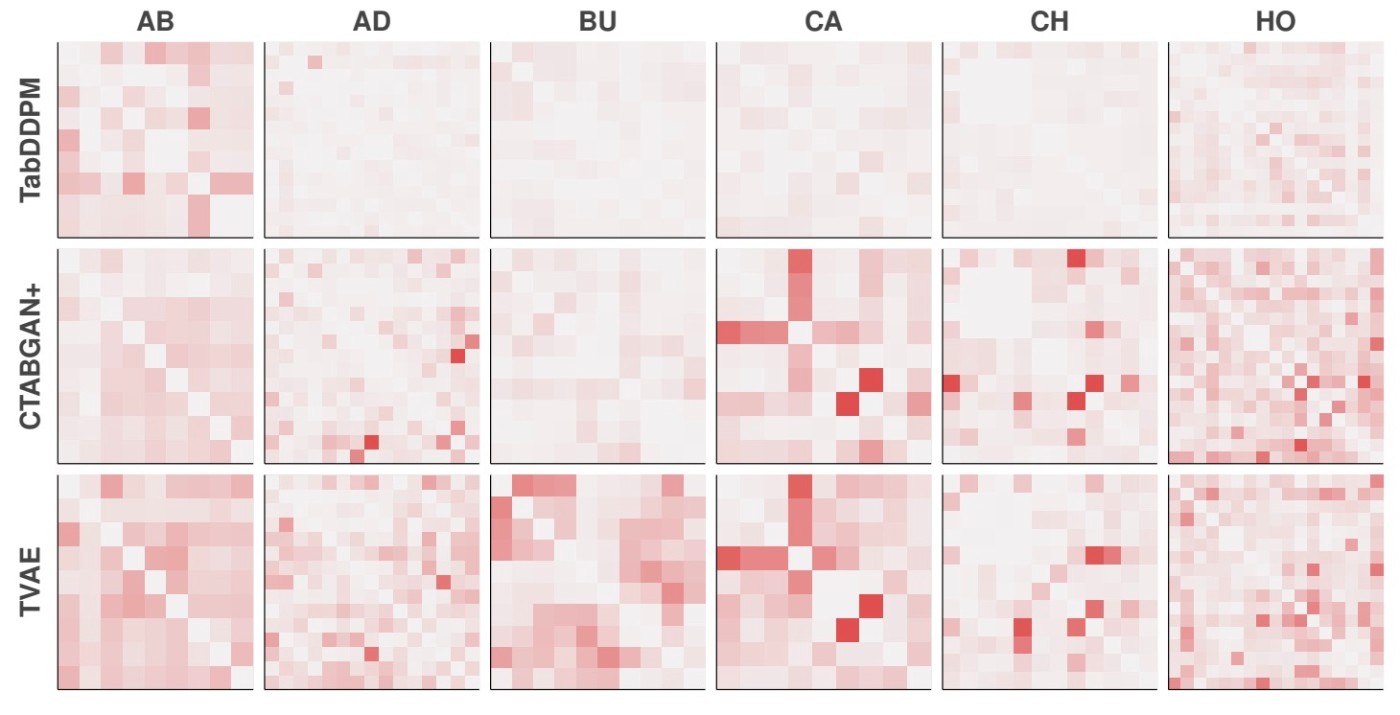
濃い赤色であるほど実データとの相関値の差が大きいことを表しますが, TabDDPMはベースラインと比較して全体的に薄く, 実データとかなり似ていることが示されています. この定量的結果としてWasserstein distance (数値カラム)とJensen–Shannon divergence (カテゴリカラム), そして相関行列間のL2 distanceを測定しています.

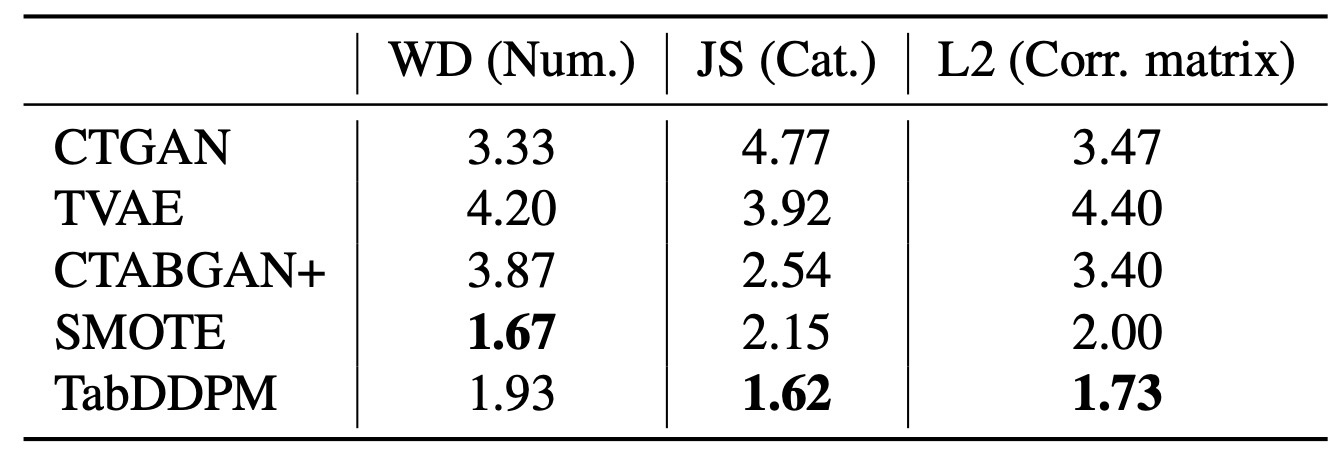
どれも低い方がいい指標ですが, TabDDPMは全体的に優れていることがわかります. WDはSMOTEの方がいいですが, SMOTEに対する優位性はこの後のプライバシーの評価で示されます.

Machine Learning Efficiency

GBDTなどのモデルを生成データで訓練し, 実データでテストします. 生成データが実データと同等の品質なら実データで訓練した場合と同じような結果が出てきます. F1 ScoreとR2 Scoreを用いて評価します.

この論文では2つのプロトコルで評価を行っています. random seedで5回行った結果が示されています.

  1. scikit-learnで提供されているMLモデル (Decision Tree, Random Forest, Logistic
    Regression (or Ridge Regression) and MLP)を用いた結果の平均値を計算する. ハイパーパラメータは一部を除きデフォルト値を使用する.

  2. 表データ分析でSoTA手法であるCatBoostとMLP architectureを用いて評価を行う. ここで言うMLP architectureは以下の式で表されます[1]. ハイパーパラメータはOptunaでチューニングを行う.

\begin{align*} &\texttt{MLP}(x)=\texttt{Linear}(\texttt{MLPBlock}(...(\texttt{MLPBlock}(x)))) \\ & \texttt{MLPBlock}(x) = \texttt{Dropout}(\texttt{ReLU}(\texttt{Linear}(x))) \end{align*}

まず, プロトコル1の結果を示します.

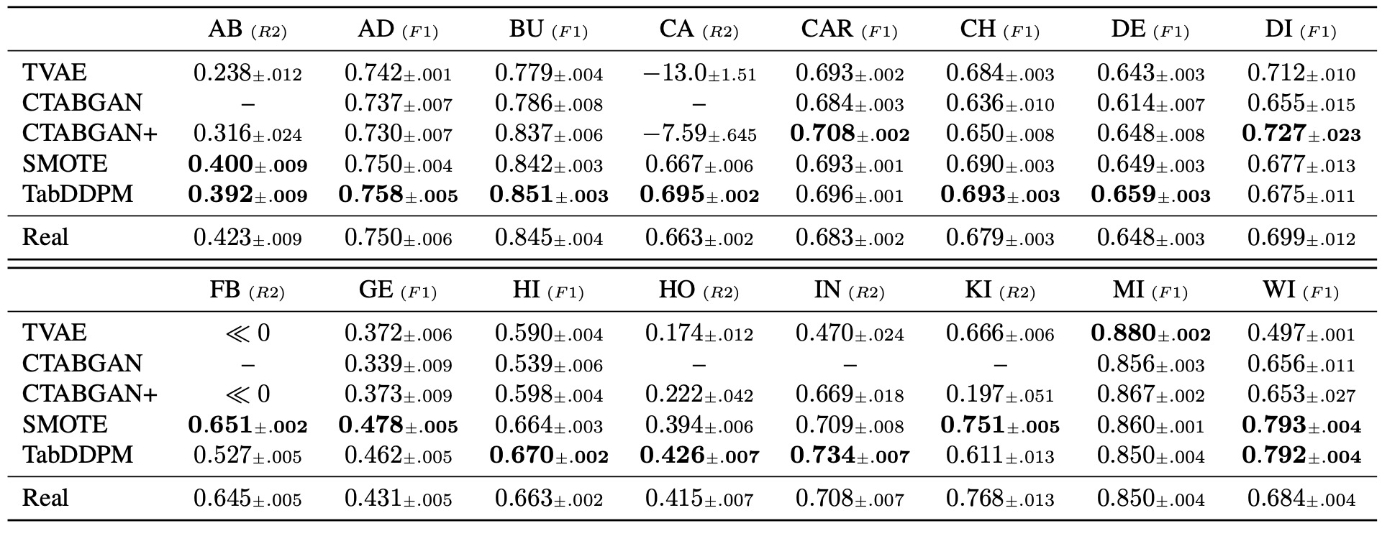
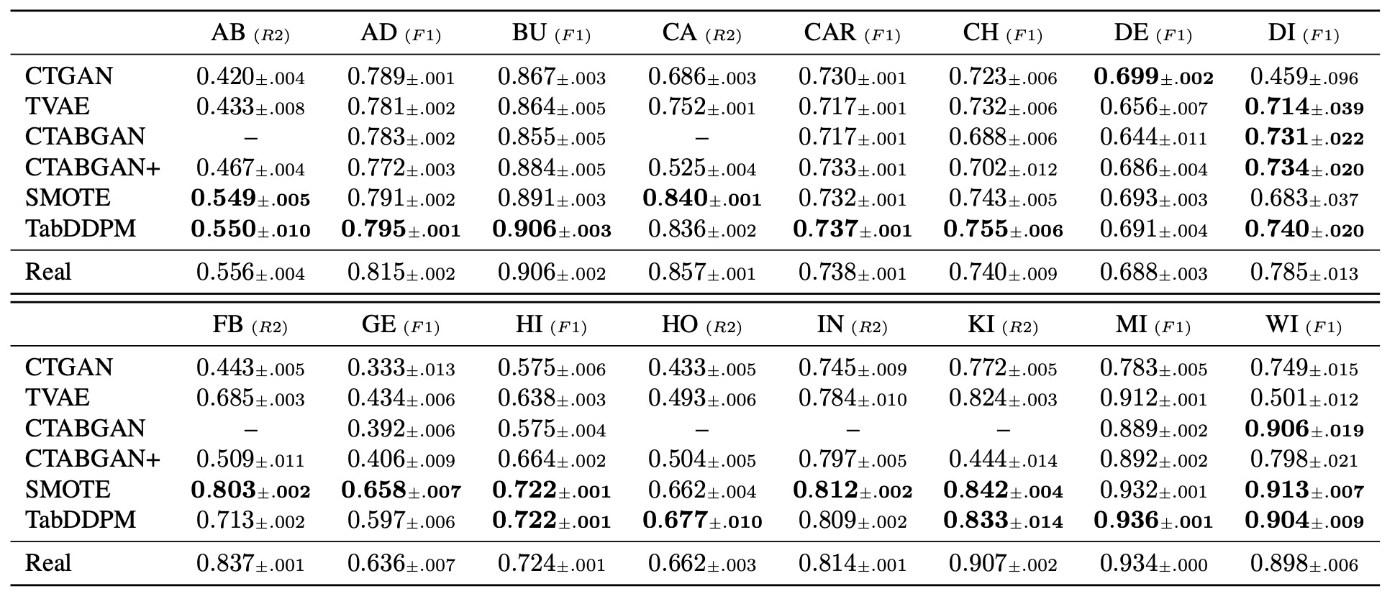
次に, プロトコル2の結果を示します. main paperの部分では恐らくページ数の制約の都合でCatBoostのみの結果が示されています. MLP architectureはAppendixにありますが, ここでは省略します.

著者らは3つの主張をしています.

  1. 2つのプロトコルを通じてほとんどのデータセットでTabDDPMはTVAEとCTABGAN+を上回るパフォーマンスである. このことは他のドメインでの既存研究通り, 拡散モデルの優位性を強調する結果である.
  2. 補完する手法であるSMOTEはTabDDPMと肉薄するばかりか, VAE/GANベースの手法を上回る生成品質である. 既存研究の多くはSMOTEとの比較がされておらず, シンプルなベースラインとして有用である.
  3. 多くの既存研究がプロトコル1での評価をしているが, SoTAモデルを用いるプロトコル2の方が評価方法として適切である. プロトコル1はSoTAモデルを使うプロトコル2と比較してパフォーマンスが悪く, 実務への適用を考えると情報量が少ない. さらに, プロトコル1はRealを上回る結果が多く, 生成データの方が価値があるように見えるが, 実務ではハイパーパラメータを適切に設定するので評価として意味があるかを検討すべきである.

個人的にはハイパーパラメータ探索をしていないプロトコル1としているプロトコル2の結果を比較することは条件が2つ違う (ハイパーパラメータを最適化している点と使用モデルが異なる点)ので少しアンフェアな気がしますが, どちらの評価方法でも提案手法が優位である点は変わらないです.

Privacy

先ほどの結果を踏まえて, TabDDPMとSMOTEのどちらが優れているのかという疑問に対しての回答を示しています. 生成データは実際のユーザ情報を含まないので, 公開しやすい. という利点が保たれているかを調査します.

Distance to Closest Record (DCR)を計算して比較を行います. 各生成データに対して実データとのL2距離の最小値を求めます. それらの平均値を取ってスコアとしています. この値が低いと実データとの距離が近く, 複製しているとみなせるそうです. ここで, このスコアだけをよくすることは簡単なので先ほどのMachine Learning Efficiencyと一緒に見ることが大事です.

さて, 結果を見てみましょう.

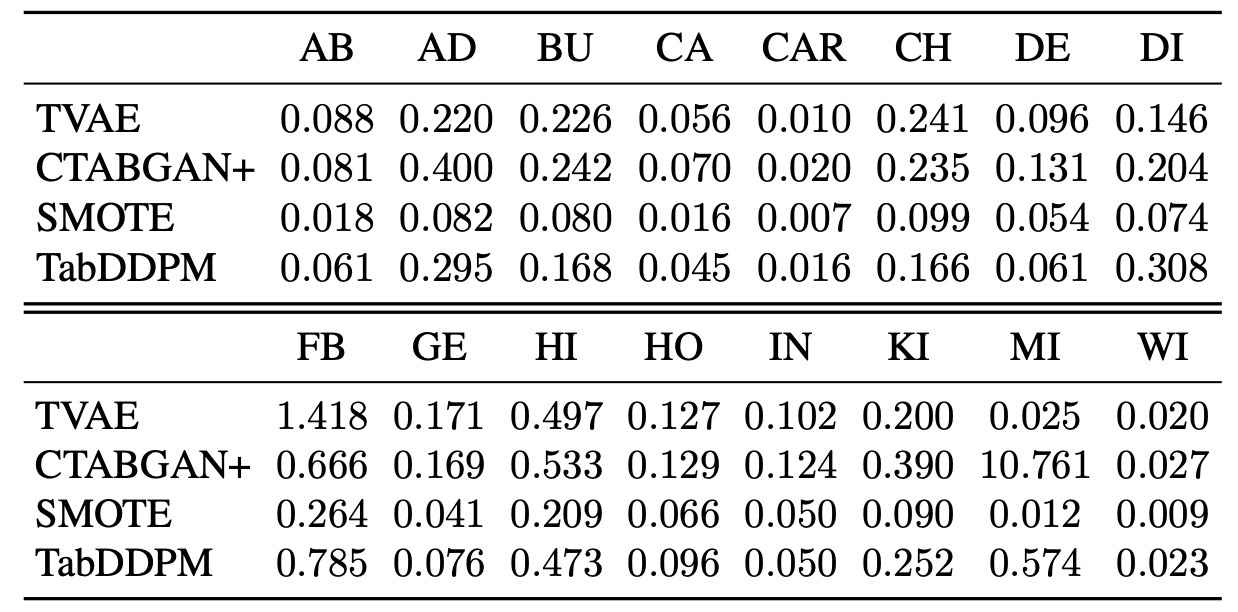
先ほどの議論から数値が高い方が良いスコアであることがわかりますが, TabDDPMとSMOTEを比較するとTabDDPMの方がプライバシーを保護していると見ることができます. その一方でVAEやGANの手法よりはプライバシーの面で劣ります. 著者らはこれについて, Machine Learning Efficiencyが悪いとDCRが高い, すなわちトレードオフの関係であると考えているようです.

実データの凸結合を計算するSMOTEの特性上, DCRが悪くなるのは必然であると言えます. これに対して著者らは実データを用いて訓練したMLPから得られる特徴量を用いてDCRを測定しました. これは画像生成のFIDなどに似た手法になります.

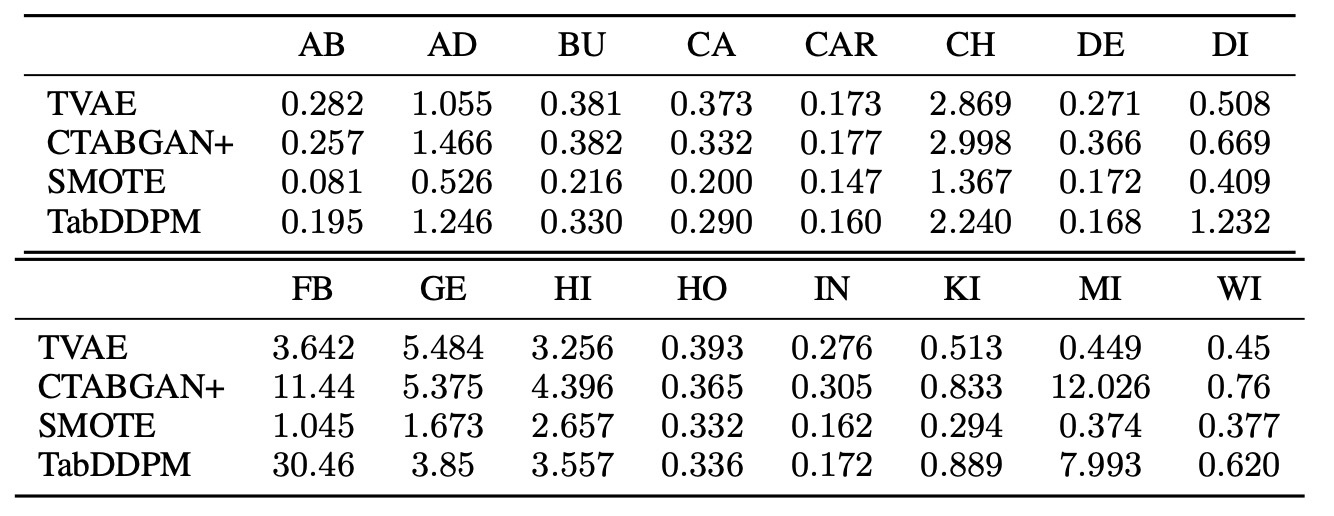
この結果を見ると特徴空間においても先ほどと同じ結果が得られています (表の小数点が一致していない点が少し気になります).

最後に, full black-box privacy attackの成功率を計測します. この攻撃は, レコードが元の訓練データに属しているかどうかを推測しています.

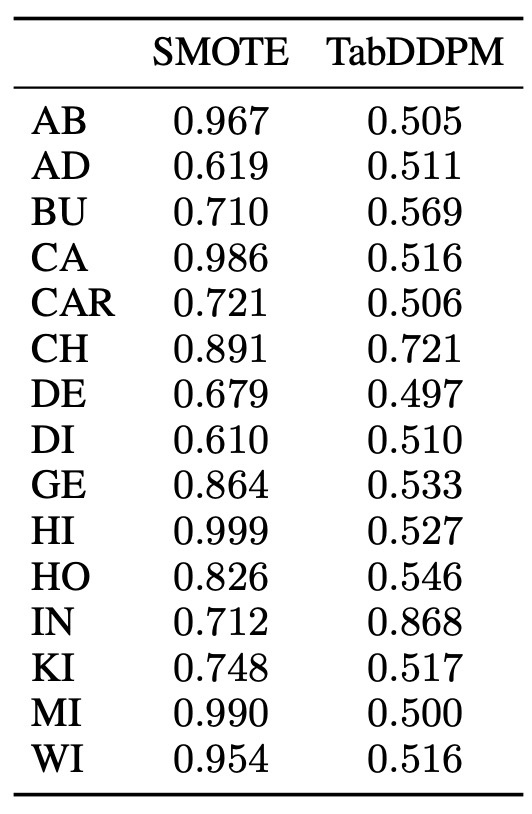
この結果を見ると, SMOTEよりもfull black-box privacy attackに対してロバストであることがわかります.

以上の結果から, TabDDPMは既存の手法と比較してプライバシーを保護しながらSoTAのMachine Learning Efficiencyを発揮できることがわかります.

まとめ

  • 表データを拡散モデルで生成するTabDDPMの提案
  • シンプルなネットワーク構造でありながら, ベースラインと比較して高品質な生成が可能である
  • 同程度の品質のSMOTEと比較してプライバシーの配慮ができている

思ったこと

  • 単純なアーキテクチャでこの品質は素晴らしい
    • MLPだけでSoTAが出ていて, 拡散モデルの強さを感じられます. 公式実装ではResNetがありますが, 論文にはResNetというワードが出てこないのでResNetではもしかしたら性能が出ないのかもしれません.
    • 論文投稿時 (2022年9月)では拡散モデルはまだこれからという感じですが, 今後アーキテクチャが洗練された場合の性能上昇が気になります.
  • 実用性なども考えられている
    • 例えば, 評価においてもMachine Leraning Efficiencyをメインに据えていたりと, 「表データを生成して何がしたいの？」に沿った評価がされている.
    • 一方で実際のデータでは欠損値があったり, 特徴量エンジニアリングをしたりしますが, その扱いなどがないのは実用性には少し欠けるかもと思います[2]. しかし, そこまでやってしまうと学問からは離れすぎてしまう気もするのでこの辺りが落とし所なのかなとも思います.
    • kaggleではLightGBMやXGBoostも使われているイメージだが, この2つの結果がないのは気になった.

参考文献

  • Kotelnikov, A., Baranchuk, D., Rubachev, I., and Babenko, A. TabDDPM: Modelling tabular data with diffusion models. In Krause, A., Brunskill, E., Cho, K., Engel- hardt, B., Sabato, S., and Scarlett, J. (eds.), Proceedings of the 40th International Conference on Machine Learn- ing, volume 202 of Proceedings of Machine Learning Research, pp. 17564–17579. PMLR, 23–29 Jul 2023.　(https://proceedings.mlr.press/v202/kotelnikov23a.html)
  • Gorishniy, Y., Rubachev, I., Khrulkov, V., and Babenko, A. Revisiting deep learning models for tabular data. Advances in Neural Information Processing Systems, 34:18932–18943, 2021.(https://openreview.net/forum?id=i_Q1yrOegLY)
  • Hoogeboom, E., Nielsen, D., Jaini, P., Forre, P., and Welling, M. Argmax flows and multinomial diffusion: Learning categorical distributions. Advances in Neural Information Processing Systems, 34:12454–12465, 2021 (https://proceedings.neurips.cc/paper/2021/hash/67d96d458abdef21792e6d8e590244e7-Abstract.html)
脚注

  1. https://openreview.net/forum?id=i_Q1yrOegLY で示されている式です. ↩︎

  2. 公式実装内では数値データは平均値埋めかdropする, カテゴリデータは最頻値で埋めるという処理が書かれていますが, 論文内ではそのような記述はなさそうです. ↩︎

Discussion