🀄

麻雀の多面待ちのパターンをすべて求めてみた(理論)

2022/10/15に公開

麻雀

tech

はじめに

先日、結果編として記事を書いたが、導出過程について記述していく。

※過去に書いた記事を、既約の定義を明確にして書き直したものである。

求めたいこと

このサイトに7枚待ちに関するパターン全19種類が載っている。これを応用して10枚と13枚待ちに対してどうなるかを求める(ついでに1枚と4枚も求める)。

用語の定義

用語	意味
手牌	考える対象の牌の形
順子	三つ組 (n, n + 1, n + 2)
刻子	三つ組 (n, n, n)
面子	順子 or 刻子
雀頭	二つ組 (n, n)
雀頭接続順子	5つ組 (n, n, n, n + 1, n + 2) or (n, n, n, n - 1, n -2)
正規形	手牌の枚数を 3 で割ったあまりが 1 となる手牌
非正規形	手牌の枚数を 3 で割ったあまりが 2 となる手牌
和了形	手牌が正規系の場合は 1 雀頭 n 面子、非正規系の場合 0 雀頭 n 面子となる形
有効牌	向聴数が上がる牌。ただし、手牌で4枚使っている場合は有効牌とはみなさない
待ち	正規形の場合は有効牌、非正規形の場合は(手牌に関係ない色の)雀頭を付け加えた手牌での有効牌
聴牌形	待ちが一枚でもある手牌
待ち送り系	和了形かつ聴牌形
待ち	正規形の場合は有効牌、非正規形の場合は(手牌に関係ない色の)雀頭を付け加えた手牌での有効牌
長さ	手牌の最大数字 - 手牌の最小数字 + 1
前方重心	手牌が左右対称形 or 各数字の枚数で並べたとき、前方に大きい数字がきている手牌
左接地	手牌の最大数が 9 であること
右接地	手牌の最小数が 1 であること
両接地	左接地 and 右接地
基本形	前方重心 and (長さ 8 以上 or 手牌の最小数が 2 である)

求める前の考察

基本形

平行移動や左右反転させた手牌は同じとみなしたい。なので、基本形を定義してその形のみを考える。

平行移動

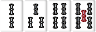
これらの手牌は両方ともノベタン待ちである。このように平行移動したパターンは同じとみなしたい。

手牌の長さが 7 以下の時は、最小の数字が 2 であるようなものだけを見ればよい
手牌の長さが 9 の場合は、平行移動がそもそもできないので全て見る
手牌の長さが 8 の場合は、左接地と右接地それぞれ見る

対称形

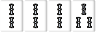
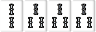
これらの手牌は左右反転しているだけなので実質同じ待ちである。その時は前方に重心があるものを採用する。例だと前者を採用する。

既約

今回の肝となる既約について。

手牌が、

正規系の場合は、面子既約かつ雀頭既約かつ雀頭接続順子既約であるとき
非正規系の場合は、面子既約であるとき

既約であるという。各種の既約については下記参照。

面子既約

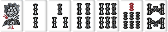
この手牌の待ちは14索待ちである。678索はあってもなくても待ちに関係ない。なので、この手牌はパターンに含めたくない。
任意の面子を省いても待ちが変わらない時、面子既約という。

雀頭既約

このパターンを考えると、待ちは147索で雀頭の9索は関係ない。なので、この手牌は雀頭既約ではない。

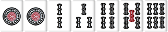
非正規系の手牌を用いて、この形とみなせるためである。

上記の例は雀頭が待ちになっていなかったパターンだが、次のパターンは雀頭が待ちになっているやつである。

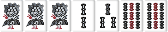
雀頭の9索が待ちになっているが、9索である必要はない。このように、任意の雀頭を別の色に置き換えても待ちが引き継がれる場合は雀頭既約とはみなさない。

任意の雀頭を省いても「待ちが変わらない、もしくは待ちか引き継がれる」ときに雀頭既約という。

雀頭接続順子既約

このパターンは雀頭既約である。1索や9索の雀頭を除くと、4索や6索の待ちがなくなるためである。ただ、78999索の部分は 67888索でもいいので、雀頭接続順子も既約の概念を入れる。

任意の雀頭接続順子を省いても「待ちが変わらない、もしくは待ちか引き継がれる」ときに雀頭接続順子既約という。

余談(前回求めたときとの違い)

過去に書いた記事との違いを記述しておく。

4枚使いしていても待ちとみなす
当該の部分を別の色に変えても待ちの種類数が変わらない
待ち送り系の場合は雀頭だけを考える

この3点が当記事と違っている。

4枚使いの扱いと、待ちの種類数について。

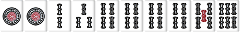
この手牌を考えると、4索が4枚使いされていて、実質の待ちとしては17索である。その状態で4索の刻子を省くと147待ちとなって待ちが変わる。ただ、過去の定義だと、147待ちのままとなって既約になっていなかった(なのでカウントされていなかった)。このように、4枚使いの牌を省くことによって待ちになることを待ち昇格と名付ける。

過去の記事では、面子などを除去すると待ちの種類数が増えることがないという前提だったが、上記のように4枚使いの定義を変えることで増えることがあるので、待ちの種類数で判別すると不都合が出てくる。なので、待ち昇格するときは問答無用で待ちが変わるとした。

待ち送り系について

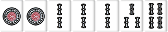
非正規系の手牌で和了形になっている場合は雀頭にも待ちがある。

その時は、雀頭を雀頭接続順子に置き換えることによって違うパターンができる。前回は数え上げなかったが、今回は全ての待ちパターンを洗い出すということで数え上げることにする。

結果

全ての取りうる手牌に対して、基本形であり既約であるものを求めた。
待ちパターンの全リスト

手牌の枚数	パターン数	リストアップ数
1	1	1
4	6	6
7	19	19
10	79	82
13	203	219
計	308	327

※リストアップ数は長さ8の手牌に対して、左接地と右接地の両方のパターンを洗い出したものである。

ここから、麻雀の多面待ちパターンは308通りあることが分かった(国士無双形を含めると309通り)。

番号付け

番号の付け方についての解説。
洗い出した待ちバターンについて、下記の順に並び変えて番号を割り振っている(上にあるほど優先度が高い)。

下処理として、長さ8の右接地している手牌で、左接地しても既約のままになるやつは番号づけのリストから除外しておく。

手牌を正規系にしたときの枚数の少ない順
手牌の枚数の少ない順
手牌を左接地させ、手牌を数字の枚数のリストとみたときの逆辞書式順

待ちの表記法

表記法を用いることによって、全ての待ちについて記号化することができる。
表記法についての解説

補足として、任意の聴牌形について一意に待ちパターンが定まるかというと、実はそうではない。

このパターンを考えると、234索を省いて3索の単騎待ち(W001-3)、3索雀頭を省いて3索のカンチャン待ち(W004)、の2パターンができる。
この場合、面子除去を優先させれば一意に定まるので、なにか制約を付け加えることによって一意に定められないかと、研究中である。

おまけ

名前がついている待ち

番号	手牌	待ち	名前
W001		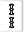	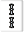単騎待ち
W002			シャンポン待ち
W003			両面待ち
W004			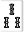カンチャン待ち
W007		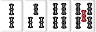	ノベタン
W009		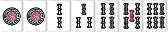	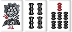三面張
W026			ノベタン三面張
W224			純正九蓮宝燈
W214			八蓮宝燈
W217-l			八蓮宝燈
W217-r			八蓮宝燈
W288			七蓮宝燈
W302			七蓮宝燈

特別な待ち

番号	手牌	待ち	説明
W031		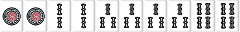	他力本願待ち(自色で待ちがない)
W109		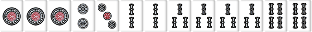	他力本願待ち(自色で待ちがない)
W219-l			13枚使って一番待ち枚数が少ない(3種6枚)
W219-r			13枚使って一番待ち枚数が少ない(3種6枚)
W261		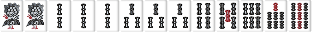	13枚使って一番待ち種が少ない(2種7枚)
W225			13枚使って一番待ち種が少ない(2種7枚)
W226-l			13枚使って一番待ち種が少ない(2種8枚)
W226-r			13枚使って一番待ち種が少ない(2種8枚)

非正規系

非正規系で待ち送り系ではないパターンは3通り。

番号	手牌	待ち
W003
W004
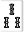W009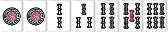

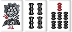待ち送り系の場合は雀頭に待ちがあり、手牌の枚数が5枚か8枚なら雀頭接続順子もリストに入る。

番号	手牌	待ち	番号	手牌	待ち
W002
W008		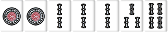	W027
W028		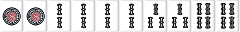	W106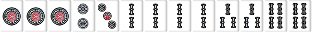
W029		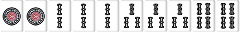	W107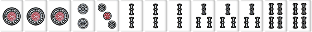
W030		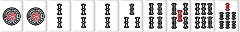	W108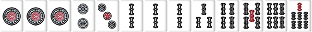
W031		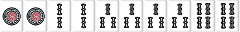	W109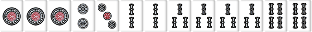
W032		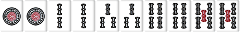	W110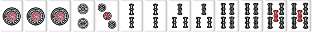
W033		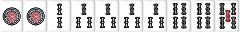	W111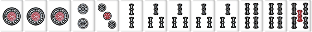
W034		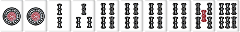	W112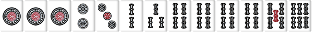
W113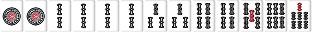
W114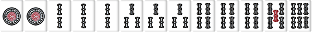
W115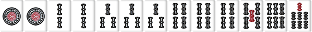
W116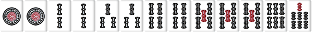
W117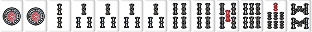
W118-l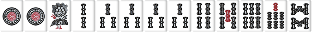

あとがき

前回書いた記事が思っていたより伸びたのでリメイクしてみた。前回は、ぱぱっと文字列のリストで済ませたが、今回は画像にして見やすいようにした。
今回、(おそらく)全てのパターンを洗い出せたが、まだまだ研究の余地はある。記事中にもあるように、任意の手牌に対して一意に待ち番号を割り振るにはどのような制約を付け加えればいいのか、それを今研究している。

また、各待ちパターンについて、関係性を調べつつ考察されている記事もある。
そういうアプローチもあり、まだまだ待ちパターンの研究は始まったばかりである。

これを機に、待ちパターンにについての考察が活発になれば嬉しい限りです。