前置き
“お行儀の良い”関数型プログラミング言語があるとします。
型を対象とし、射を関数とし、射の等しさを関数の外延的な等しさとし、射の合成を関数合成とし、恒等射を恒等関数とするとこれは圏を成します。
この事実は、圏論を使ってプログラミングを説明するときに大いに役立ち、プログラミングについての理解を深めることができます。
本記事では、その逆を目的としています。
つまり、プログラミングの知識を圏論の理解に役立てようという趣旨です。
関数合成と恒等関数
プログラミングでは関数合成と恒等関数を定義することができます。
関数合成は2つの関数を引数に取り、関数を返す操作です。
関数合成は一方の終域と他方の始域が一致している場合にのみ定義されます。
関数 f と g の合成を g \circ f と書きます。
f : A → B と g : B → C のとき、g \circ f の型は A → C です。
合成関数は任意の x : A について f を適用した後に g を適用したものを返します。
_∘_ : (B → C) → (A → B) → (A → C)
g ∘ f = λ a → g (f a)
本記事では x : A に関数 f: A → B を適用した結果を f(x) ではなく f \space x と書くので注意してください。
恒等関数 \mathrm{funcid}_{X} は任意の型 X に対して定義できる関数で、その型は X → X です。
恒等関数は任意の要素 a : X に対してそのまま a を返します。
funcid : X → X
funcid = λ a → a
2つの関数 f : A → B と g : A → B について、任意の入力 x : A に対する出力 f \space x と g \space x が常に一致するとき、f と g は外延的に等しいと言います。
本記事では、関数に対して f = g と書くときは外延的な等しさを意味することとします。
圏
圏の定義も念のため書いておきます。
圏は射と呼ばれる“何か”がいくつかの性質を満たすもののことを言います。
射は対象と呼ばれる“何か”を2つ持ち、一方を射の域、他方を射の余域と言います。
任意の対象 A と B について、A を域、B を余域とする射を「A から B への射」と言います。
f が A から B への射であることを f : A ⇒ B と書くことにします。
※記号 ⇒ を用いる表記はあまり一般的ではなく、通常は f : A → B と書くことが多いと思いますが、本記事では記号 → を関数を表す記号として留保します。
A から B への射は一般に複数存在するので、便宜上それ全体を表す用語が欲しいです。
ここではそれをA から B へのホムと呼び、A ⇒ B と書きます。
2つの射は、同じホムに属している場合に限り、その“等しさ”が定義されます。
言い換えると、その域が一致し、かつその余域も一致するときに定義されます。
域や余域が異なる場合、射の等しさは考えません。
「2つの射が等しいとは何か?」は圏を定義するときに決めます。
f と g が等しいとき、f = g と書きます。
射には合成と呼ばれる演算 (- \circ -) が定義されます。
これは2つの射を受け取り、射を返す操作です。
射の合成は一方の余域と他方の域が一致している場合は必ず定義されますし、射の合成が定義されるのはそのときに限ります。
射 f : A ⇒ B と g : B ⇒ C の合成を g \circ f と書きます。
これは g \circ f : A ⇒ C です。
射の合成は以下の性質を満たさなければなりません。
任意の射 f : A ⇒ B, g : B ⇒ C, h : C ⇒ D に対して
(h \circ g) \circ f = h \circ (g \circ f)
が成り立ちます。
これを射の合成の結合則と言います。
※ここで射の等しさを論じていますが、左辺の射と右辺の射のホムが一致するのでその等しさを議論しても問題ありません。
域と余域が一致する任意のホム A ⇒ A は恒等射と呼ばれるある特別な射を持たなければなりません。
これを \mathrm{id}_{A} と書きます。
恒等射は任意の f : A ⇒ B について以下の性質を満たします。
f \circ \mathrm{id}_{A} = f = \mathrm{id}_{B} \circ f
射はホムの単なる要素である
プログラミングの観点からすると、射 f : A ⇒ B は、ホム A ⇒ B の単なる要素に過ぎません。
関数の場合、A の要素 x に関数 f : A → B を適用して B の要素 f \space x を得ることができます。
しかし、射 f : A ⇒ B に対してできることは射の合成だけです。
射の合成は単なる2引数関数である
プログラミングの観点からすると、射の合成は2つの射を引数にとり、射を返す関数に過ぎません。
任意の対象 A, B, C について以下の関数
(- \circ -) : (B ⇒ C) → (A ⇒ B) → (A ⇒ C)
が定義されます。
圏を定義するときは、上記関数を“実装”しなければなりません。
射の後合成
射の合成 (- \circ -) に g : B ⇒ C を部分適用してみましょう。
(g \circ -) : (A ⇒ B) → (A ⇒ C)
これは任意の射 f : A ⇒ B について、それを g で合成した結果 g \circ f を返す関数です。
これを g による後合成関数と呼び、(g \circ -) や \mathrm{post}^{g} と書くことにします。
後合成関数は射の余域を変更します。
ここでの興味深い観察は、g : B ⇒ C が引数の射の余域 B と結果の射の余域 C を指定していますが、域 A については何も指定しないということです。
つまり、\mathrm{post}^{g} は各対象 A について定義されるジェネリック関数です。
A の恒等射を \mathrm{id}_{A} と書く流儀に倣って \mathrm{post}^{g}_{A} とでも書くべきでしょう。
同様に、後合成関数 (g \circ -) の引数となる射の始域 A を明示したい場合は (g \circ -_{A}) と書くことにします。
射の前合成
同様に、射の合成 (- \circ -) を flip してから f : A ⇒ B を部分適用することにより、射の前合成
\mathrm{pre}^{f}_{C} : (B ⇒ C) → (A ⇒ C)
を考えることもできます。
本記事では割愛しますが、後合成と同じような議論が展開できます。
後合成の性質
射 g : B ⇒ C があるとき、その後合成を考えることで射から射への関数 (A ⇒ B) → (A ⇒ C) を生成することができました。
逆に、射から射への関数 (A ⇒ B) → (A ⇒ C) があるときに、これが何らかの射の後合成と見なせるための条件とは何でしょうか。
つまり、関数 α_{A} : (A ⇒ B) → (A ⇒ C) があるとき、ある射 g : B ⇒ C を用いて α_{A} = \mathrm{post}^{g}_{A} と書けるための条件とは何でしょうか。
自然性
任意の対象 z について関数 α_{z} : (z ⇒ B) → (z ⇒ C) が定義されているとします。
任意の対象 x と y および、任意の射 p : y ⇒ x と h : x ⇒ B を考えます。
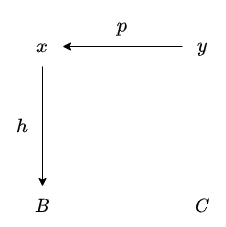
初期設定
このとき、y ⇒ C の射を得る方法が2通りあるので考えてみてください。
まず1つ目の方法です。
h に関数 α_{x} を適用することで x ⇒ C の射が得られます。
以下の図では細い矢印が射を、太い矢印が関数適用を表します。
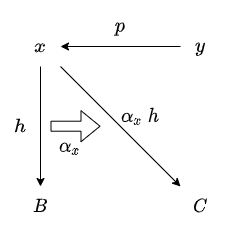
α_{x} の適用
射の合成を考えることで y ⇒ C の射が得られます。

p の前合成
続いて2つ目の方法です。
初期設定に戻り、今度は先に p と h を合成します。
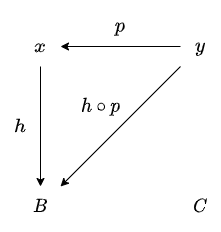
射の合成
これに関数 α_{y} を適用することで y ⇒ C の射が得られます。
ここで、α を適用する射の始域が1つ目の方法とは異なる点に注意してください。
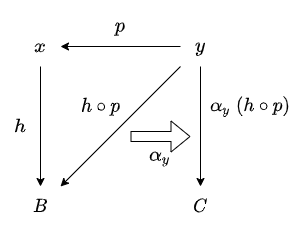
α_{y} の適用
以上により、y ⇒ C の2つの射が得られました。
- 関数を適用した後に射を合成する (α_{x} \space h) \circ p
- 射を合成した後に関数を適用する α_{y} \space (h \circ p)
もし、関数 α が何らかの射の後合成として見なせるとき、何が言えるでしょうか。
ある射 g : B ⇒ C が存在して、α_{z} = \mathrm{post}^{g}_{z} を満たすとして、先ほどの図を書き直してみます。
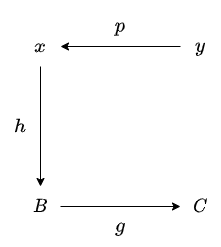
初期設定
太矢印で書いていた関数 α_{z} の適用の箇所を、すべて g の後合成で書き換えることができます。
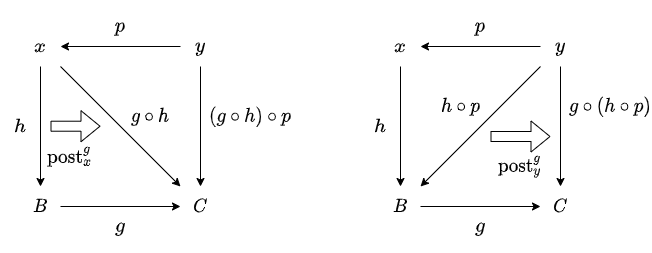
α を g の後合成で書き換える
射の合成の結合則により、(g \circ h) \circ p = g \circ (h \circ p) が成り立ちます。
したがって、もし関数 α_{z} が何らかの射の後合成と見なせるのであれば、先ほど作った2つの射は等しくなければなりません。
(α_{x} \space h) \circ p = α_{y} \space (h \circ p)
式変形をしてこの条件を少し書き換えてみましょう。
ここで左辺を式変形すると
\begin{aligned}
(α_{x} \space h) \circ p
&= ((α_{x} \space h) \circ -_{y}) \space p
\end{aligned}
となり、右辺を式変形すると
\begin{aligned}
α_{y} \space (h \circ p)
&= α_{y} \space ((h \circ -_{y}) \space p) \\
&= (α_{y} \circ (h \circ -_{y})) \space p \\
\end{aligned}
となるので
((α_{x} \space h) \circ -_{y}) = α_{y} \circ (h \circ -_{y})
とも書けます。
読むとすれば「h に α_{x} を関数適用して得られる射の後合成と、h を後合成してから α_{y} を関数適用して得られる射から射への関数は外延的に等しい」となるでしょう。
ちなみに、同様の式変形を行うことで今度は前合成の観点から成り立つ性質を得ることができます。
(- \circ p) \circ α_{x} = α_{y} \circ (- \circ p)
関数 α_{z} は任意の前合成について可換です。
以上が、関数 α_{z} を何らかの射の後合成と見なすための必要条件となります。
後合成関数から見た射
先ほどの条件
((α_{x} \space h) \circ -_{y}) = α_{y} \circ (h \circ -_{y})
では、射の合成を直接には使用していない点に注意してください。
後合成 (g \circ -) を単なる関数と見なし、\mathrm{post}^{g} のほうで書くと分かりやすいかもしません。
\mathrm{post}^{α_{x} \space h}_{y} = α_{y} \circ \mathrm{post}^{h}_{y}
ここで射の合成という概念を忘れ、代わりに射 g の後合成と呼ばれる特別な関数 \mathrm{post}^{g}_{x} : (x ⇒ B) → (x ⇒ C) の存在を直接仮定したとして、圏の性質を言い換えることができます。
合成射の後合成は、個別の射の後合成の関数合成で言い換えることができます。
\mathrm{post}^{g \circ f}_{z} = \mathrm{post}^{g}_{z} \circ \mathrm{post}^{f}_{z}
恒等射の後合成は元の射を変えないので、単なる恒等関数になります。
\mathrm{post}^{\mathrm{id}_{B}}_{A} = \mathrm{funcid}_{A ⇒ B}
射の構成
では実際に、任意の対象 z に対して定義されている関数 α_{z} : (z ⇒ B) → (z ⇒ C) が、任意の対象 x および y と任意の h : x ⇒ B について条件
((α_{x} \space h) \circ -_{y}) = α_{y} \circ (h \circ -_{y})
を満たすとき、何らかの射 g : B ⇒ C が存在して
α_{z} = \mathrm{post}^{g}_{z}
が成り立つようにできるでしょうか。
B ⇒ C の射を生成するために、α_{B} : (B ⇒ B) → (B ⇒ C) を考えます。
恒等射 \mathrm{id}_{B} に適用すると B ⇒ C の射が得られます。これを g' とおきます。
\begin{aligned}
&g' : B ⇒ C \\
&g' = α_{B} \space \mathrm{id}_{B} \\
\end{aligned}
このとき、g' の後合成を考えてみましょう。
射 g' は関数 α_{B} の適用により定義されているので、射の合成と関数適用の順番を交換できるはずです。
\begin{aligned}
\mathrm{post}^{g'}_{z}
&= (g' \circ -_{z}) \\
&= ((α_{B} \space \mathrm{id}_{B}) \circ -_{z}) \\
&= α_{z} \circ (\mathrm{id}_{B} \circ -_{z}) \\
&= α_{z} \circ \mathrm{funcid}_{z ⇒ B} \\
&= α_{z}
\end{aligned}
以上により、関数 α_{z} がまさに射 g' の後合成と外延的に等しいということが示されました。
射の合成の便利さ
以上の観察の結果を踏まえると、圏における“射の合成”の概念の便利さが見えてきます。
圏は射の合成の結合性と恒等射の存在を要求するので、これにより
((α_{x} \space h) \circ -_{y}) = α_{y} \circ (h \circ -_{y})
を満たすような関数 α_{z} があるとき、それを射の後合成と見なせるような射 α_{B} \space \mathrm{id}_{B} が必ず存在します。
逆に、そのような性質を満たす関数のことを、単なる射の後合成として書くことができるわけです。
もし射の合成の概念を忘れてしまい、射の後合成を射から射への関数で記述しなければならなくなったとすると、上記の条件を至るところで要求しなければなりません。
また、射から射への関数の関数合成の話を、単なる射の合成に帰着できるのも便利な点です。
これは
(g \circ -) \circ (f \circ -) = ((g \circ f) \circ -)
が成り立つからです。
同型射
この流れで同型射を言い換えてみます。
2つの射 f : A ⇒ B と g : B ⇒ A が
\begin{aligned}
g \circ f &= \mathrm{id}_{A} \\
f \circ g &= \mathrm{id}_{B} \\
\end{aligned}
を満たすとき、f と g は同型射であると言います。
2つの対象の間に同型射が存在するとき、それらを同型であると言い、A \cong B と書きます。
圏論の言葉で書くと非常に簡潔ですね。
ところで、これらの条件が成り立つとき、任意の h : x ⇒ A と h' : y ⇒ B について
\begin{aligned}
g \circ f \circ h &= h \\
f \circ g \circ h' &= h' \\
\end{aligned}
が成り立つので、以下のように書けます。
\begin{aligned}
(g \circ -_{x}) \circ (f \circ -_{x}) &= \mathrm{funcid}_{x ⇒ A} \\
(f \circ -_{y}) \circ (g \circ -_{y}) &= \mathrm{funcid}_{y ⇒ B} \\
\end{aligned}
この事実を使って、同型射の概念を、射の合成を直接使わずに関数の観点から記述してみます。
関数 α_{z} : (z ⇒ A) → (z ⇒ B) が存在して、条件
\begin{aligned}
((α_{x} \space h) \circ -_{y}) = α_{y} \circ (h \circ -_{y}) \\
\end{aligned}
を満たすとし、同様に関数 β_{z} : (z ⇒ B) → (z ⇒ A) が存在して条件
\begin{aligned}
((β_{x} \space h) \circ -_{y}) = β_{y} \circ (h \circ -_{y}) \\
\end{aligned}
を満たすとします。更にこれらの関数合成の結果は恒等関数と外延的に等しくなるとします。
\begin{aligned}
β_{x} \circ α_{x} &= \mathrm{funcid}_{x ⇒ A} \\
α_{y} \circ β_{y} &= \mathrm{funcid}_{y ⇒ B} \\
\end{aligned}
このとき、関数 α_{z} と β_{z} を用いて同型射を復元できるでしょう。
したがって、そのような α と β が存在することを以って A \cong B を言うことができます。
ちなみに、同様の議論が射の前合成でも展開でき、射から射への関数を射の前合成と見なせるための条件や同型射の概念を導出できます。
まとめ
射の後合成が持っている性質と、射から射への関数を射の後合成と見なせるための条件について観察しました。
これに派生して、射から射への関数の存在から同型を言うための条件についても観察しました。
もし本記事が参考になりましたら、いいねあるいはコメントよろしくお願いします。







Discussion