本記事は,以下の書籍の内容を参考にした勉強メモです.
https://www.kspub.co.jp/book/detail/1565715.html
重要な議論を飛ばして結論先行で書いていますので,誤り等ありましたらコメントください.
確率変数
定義
(実数値の)確率変数Xとは,確率空間(\Omega, \mathcal{F}, P)から可測空間(一般的にn次元ユークリッド空間とボレル集合族 (\mathbb{R}^n, \mathcal{B}(\mathbb{R}^n)) )への関数を確率変数と呼び,以下で定義される.
\begin{align}
\{\omega\in\Omega:X(\omega)\leq\lambda\}\in\mathcal{F}
\end{align}
ボレル集合族とは,実数全体の開区間に対する \sigma-加法族なので,上の定義を以下のように書き換えることができる.
\begin{align}
\{\omega\in\Omega:X(\omega)\in(a,b)\} & = \\
\{\omega\in\Omega:X(\omega)> a\}\cap\{\omega\in\Omega:X(\omega)< b\} & = \\
\{\omega\in\Omega:X(\omega)\leq a\}^\mathcal{C}\cap(\bigcup_{n=1}^\infin\{\omega\in\Omega:X(\omega)+\frac{1}{n}\leq b\}) & \in\mathcal{F}
\end{align}
式(4)は式(1)と\sigma-加法族の定義の2つ目と3つ目から導出される.
再掲 \sigma-加法族 \mathcal{M}の定義
\begin{align}
1.& \emptyset\in\mathcal{M} \\
2.& A\in\mathcal{M} => A^\mathcal{C}\in\mathcal{M} \\
3.& \bigcup_n^\infin A_n = A_1\cup A_2\cup ... \in\mathcal{M}
\end{align}
なぜ確率変数?
確率空間 (\Omega, \mathcal{F}, P)上の確率変数 Xとは,標本空間から実数への関数 X: \Omega \rarr \mathbb{R}である.この関数による変換はなくても問題ない.しかし,前回触れた通り,確率空間の \sigma-加法族 \mathcal{F}はある よい性質 をもつ必要がある.そのため,確率変数とそこから生成される \sigma-加法族を
\begin{align}
\sigma[X] &= \{X^{-1}(G):G\in\mathcal{G}\} \\
&= \{\{\omega\in\Omega:X(\omega)\in\Omega\}:G\in\mathcal{G}\}
\end{align}
とし,これ用いて新たな確率空間 (\Omega, \sigma[X], P) を考える.また,これにより標本空間 \Omegaは十分に大きければなんでもいいことにできる.
この上での確率測度も P(X^{-1}(\{\omega\}))を適当に定めることで決まる.
確率と確率変数
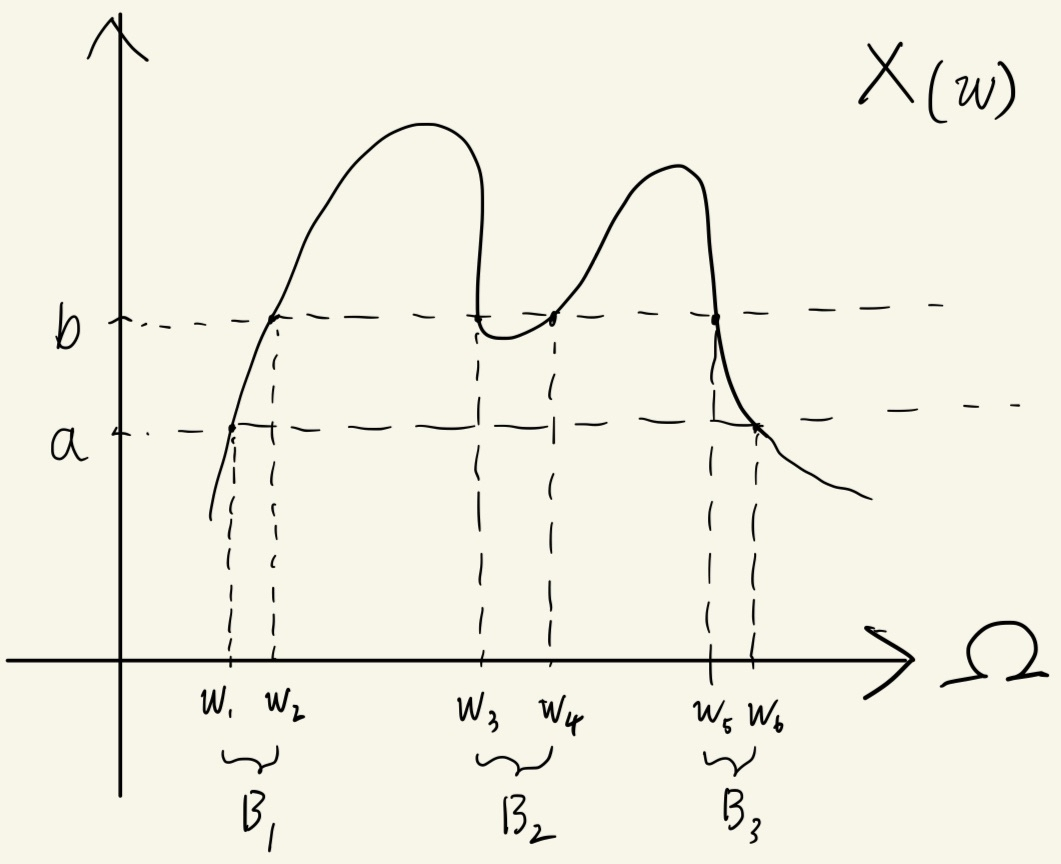
式(2)の状況において,確率空間 (\Omega, \sigma[X], P) において確率測度 P(X^{-1}(\{\omega\}))を求める場合を考える.上の図から, X(\omega)\in(a,b) となる標本集合を以下で表すことができる.
\begin{align}
B &= \bigcup_{i=1,2,3}B_i \\
&= [\omega_1,\omega_2]\cup[\omega_3,\omega_4]\cup[\omega_5,\omega_6]
\end{align}
したがって, P(X^{-1}(\{\omega\})) = P(B) を適当に決めることになる.
期待値
確率空間 (\Omega, \mathcal{F}, P)上の確率変数 Xの期待値とは,上の図にあるグラフの下側の面積を求めることに相当する.また,式(10)にある集合 B上にだけ制限した期待値も同様に求められる.このため,確率変数に対する積分をルベーグ積分を用いて考える.
準備
ルベーグ積分を定義する準備として,単関数とその積分を説明する.
単関数と積分
単関数 f とは測度空間 (S, \mathcal{M}, \mu) 上で定義される関数であり,有限個の値 a_1,…,a_n と非交差的な可測集合 B_1,…,B_n\in\mathcal{M} を用いて以下のように書ける.
f(x) = \sum_{j=1}^na_j\mathbf{1}_{B_j}(x)
この単関数の積分は以下で定義される.
\int_Sf(x)\mu(dx) = \sum_{j=1}^na_j\mu(B_j)
ルベーグ積分
まず,確率変数の定義式(1)と単関数の定義から,確率変数を単関数で近似する.

まず確率変数の値域を n 以上と n 未満に分け, n 未満を n 等分し,単関数 f_n を以下のように作る.
f_n(x) = \sum_{j=1}^{n2^n}a_{j-1}\mathbf{1}_{\{a_{j-1}\leq f\leq a_j\}} + n\mathbf{1}_{n\leq f}(x)
この単関数 f_n は, \lim_{n\rarr\infin} と極限をとることで,元の関数 f に近づく.
期待値の計算
ルベーグ積分を用いて確率変数から期待値 E[X] は以下のように導出される.
\begin{align}
E[X] &= \int_\Omega X(\omega)P(d\omega) \\
&= \lim_{n\rarr\infin} \int_\Omega X_n(\omega) P(d\omega) \\
&= \lim_{n\rarr \infin} \sum_{n}\{a_{n-1}\mathbf{1}_{\{a_{j-1}\leq f\leq a_j\}} + n\mathbf{1}_{n\leq f}(x)\}
\end{align}
まとめ
- 確率変数とは,標本から事象への関数であり,これに基づいてよい性質を持つ \sigma-加法族を構築できる.
- 確率変数の期待値は,確率変数のグラフの下側の面積である.
- 期待値の計算には,確率密度を単関数で近似し,ルベーグ積分によって求める.


Discussion