Zenn
🌊

【入門】フローマッチングのエッセンス

に公開
機械学習
ディープラーニング
拡散モデル
生成 AI
フローマッチング
tech

はじめに

2025年、生成AIの世界は新たな変革期を迎えています。拡散モデルが切り拓いた高品質なデータ生成の地平は、さらに効率的で柔軟な「フローマッチング（Flow Matching, FM）」というパラダイムへと進化を遂げようとしています。Meta AIが発表した「Flow Matching Guide and Code」(arXiv:2412.06264v1) は、このフローマッチングの数学的基盤から最新の拡張、さらにはPyTorchによる実装までを網羅した包括的なガイドであり、本記事はこのガイドを元に、フローマッチングのエッセンスを可能な限りわかりやすく紐解いていくことを目指します。

前回の記事「【入門】拡散モデルのエッセンス」では、ノイズからデータを徐々に復元する拡散モデルの本質に迫りました。フローマッチングは、その拡散モデルの考え方をさらに一般化し、より直接的かつ効率的にデータ間の「流れ」を学習する枠組みを提供します。画像、動画、音声、テキスト、さらにはタンパク質構造のような生物学的データまで、多様なドメインで最先端の性能を達成しており、まさに次世代の生成AIを駆動するコア技術と言えるでしょう。

本記事は、拡散モデルの基礎を理解された方が、次のステップとしてフローマッチングの世界へスムーズに移行できるよう構成されています。数式の厳密な導出や詳細な理論展開については、ぜひ上記のMeta AIのガイド（原著）や関連論文をご参照ください。

この記事が、皆様にとってフローマッチングというフロンティアを切り拓くための礎となり、そして生成AIのさらなる可能性を探求する旅の一助となることを願っています。

本記事の構成

  • 第1章 フローマッチングへようこそ：新時代の生成モデリング
  • 第2章 フローの数理：フローマッチングの基礎を固める
  • 第3章 フローマッチングの核心：理論とアルゴリズム
  • 第4章 フローマッチングの拡張(1)：多様体上の流れ
  • 第5章 フローマッチングの拡張(2)：離散空間への挑戦
  • 第6章 フローマッチングの一般化：ジェネレータマッチング
  • 第7章 フローマッチングと拡散モデル：共通点と相違点

さあ、フローマッチングが織りなす連続的な変化の魔法を、数式という羅針盤を手に解き明かしていきましょう。

第1章 フローマッチングへようこそ：新時代の生成モデリング

この章のゴール：
この章では、フローマッチング（FM）の基本的なアイデアとその魅力を紹介します。拡散モデルとの関係性を概観しつつ、FMがなぜ注目されているのか、どのような利点があるのかを探ります。そして、FMの核となる「確率パス」と「速度場」の概念を、簡単な例を通して直感的に理解することを目指します。この章を読むことで、FMがどのようにしてデータ間の滑らかな変換を実現しようとしているのか、その全体像を掴むことができるでしょう。

（原著の §2 "Quick tour and key concepts" に相当する内容です。）

1.1 フローマッチングとは何か？：流れに乗ってデータを変換する

フローマッチング（Flow Matching, FM）とは、一言で言えば、ある確率分布（例えば、単純なノイズ分布）から別の確率分布（例えば、複雑な画像データの分布）へとサンプルを連続的に変換する「流れ（フロー）」を学習する生成モデリングのフレームワークです。

この「流れ」は、時間とともに変化するベクトル場（速度場）によって定義される常微分方程式（Ordinary Differential Equation, ODE）の解として数学的に記述されます。FMの目標は、このODEを駆動する速度場をニューラルネットワークでパラメータ化し、訓練データを用いて学習することです。

一度この速度場が学習されれば、既知の分布（ソース分布 p_0）からサンプルを一つ取り出し、ODEを解く（シミュレーションする）ことで、目標分布 p_1 に従う新しいサンプルを生成することができます。


図1.1：フローマッチングの基本概念。ソース分布 p_0（左、例：ノイズ）のサンプル X_0 が、学習された速度場 u_t(X_t) に従って時間 t=0 から t=1 へと流れることで、ターゲット分布 p_1（右、例：画像）のサンプル X_1 に変換される。この変換経路が確率パス p_t に対応する。

1.1.1 拡散モデルとの関係性

拡散モデル（特にDDPMやSBM）も、ノイズからデータを生成するという点でFMと似ています。実際、第7章で詳しく見ますが、拡散モデルの多くはFMの特殊なケースとして捉えることができます。

  • 拡散モデル: 通常、固定されたノイズ付加プロセス（拡散過程）とその逆のノイズ除去プロセス（逆拡散過程）を考えます。逆拡散過程は、しばしば確率微分方程式（SDE）または対応するODE（確率フローODE）で記述され、そのスコア関数またはノイズ予測モデルを学習します。
  • フローマッチング: より一般的に、ソース分布 p_0 とターゲット分布 p_1 を結ぶ「確率パス」p_t （t \in [0,1] で p_0 から p_1 へと滑らかに変化する分布の列）を設計し、この確率パスを生成するようなODEの速度場 u_t を直接学習します。

FMは、拡散モデルで暗黙的に仮定されていた確率パスや速度場をより明示的に扱い、その設計自由度を高めることで、学習の効率性や生成品質の向上を目指します。特に、シミュレーションフリーな学習が可能である点が大きな利点です。

1.1.2 なぜフローマッチングなのか？その利点

FMが注目される主な理由は以下の通りです。

  1. シミュレーションフリーな学習: 多くのFMの手法では、学習時にODEを解く必要がありません。これは、特定の条件下でターゲットとなる速度場を直接回帰問題として学習できるためです（詳細は第3章）。これにより、学習が高速かつ安定します。拡散モデルのスコアマッチングもシミュレーションフリーでしたが、FMはより広範な確率パスの選択肢を提供します。
  2. 設計の柔軟性: ソース分布 p_0、ターゲット分布 p_1、そしてそれらを結ぶ確率パス p_t の選び方に大きな自由度があります。これにより、タスクに応じた最適な変換経路を設計できます。例えば、最適輸送（Optimal Transport, OT）の理論を取り入れた確率パスは、より「まっすぐな」変換を促し、サンプリング効率の向上に繋がります。
  3. 強力な性能: 画像、動画、音声、3D形状、分子構造など、様々なデータモダリティで最先端の生成品質を達成しています。
  4. 理論的明快さ: 連続正規化フロー（Continuous Normalizing Flows, CNF）のアイデアを基盤としつつ、その学習の難点を克服する形で発展しており、数学的な見通しが良いとされています。

1.2 クイックツアー：フローマッチングの2つのステップ

原著では、フローマッチングのレシピを2つの主要なステップで説明しています（原著 §2, Fig. 2）。


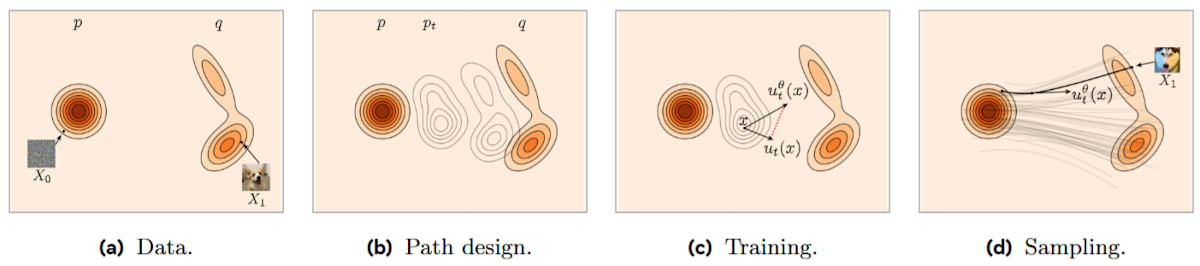
図1.2：フローマッチングの設計図。(a) 既知のソース分布 p から未知のターゲット分布 q へとサンプルを変換するのが目標。(b) p_0=p と p_1=q を結ぶ時間連続な確率パス (p_t)_{0 \le t \le 1} を設計する。(c) p_t を生成する速度場 u_t を回帰により推定する。(d) 推定された速度場 u_t^\theta(X_t) を t=0 から t=1 まで積分（ODEを解く）することで、新しいターゲットサンプル X_1 \sim q を生成する。 (Meta AI "Flow Matching Guide and Code" Fig. 2 より引用)

  1. ステップ1：確率パスの設計

    • 既知のソース分布 p_0（例：標準正規分布 \mathcal{N}(x|0, I)）と、学習データが従うターゲット分布 p_1=q を用意します。
    • これら2つの分布を滑らかに補間する時間連続な「確率パス」p_t(x) を定義します。これは、t=0 で p_0(x) に一致し、t=1 で p_1(x) に一致するような、分布の連続的な変化を表します。
    • 原著の例では、「条件付き最適輸送パス」または「線形パス」と呼ばれるものが紹介されています。これは、ソースサンプル X_0 \sim p_0 とターゲットサンプル X_1 \sim p_1 を用意し、それらの線形結合 X_t = (1-t)X_0 + tX_1 を考えることで、X_t \sim p_t となるような確率パスです。このとき、各時刻 t における p_t(x) は、条件付き確率パス p_{t|1}(x|x_1) (あるターゲットサンプル x_1 に条件付けられたパス) を q(x_1) で平均したものになります。
      具体的には、p_{t|1}(x|x_1) = \mathcal{N}(x|tx_1, (1-t)^2 I) のような形を取ります（原著 Eq. 2.2, 2.5）。これは、t=0 では \mathcal{N}(x|0, I) (つまりp_0) になり、t=1 では x_1 に集中するデルタ関数 \delta_{x_1}(x) に近づきます。

  2. ステップ2：速度場の学習

    • 確率パス p_t(x) は、ある時間依存の速度場 u_t(x) によって駆動されるODE \frac{dX_t}{dt} = u_t(X_t) の解として得られると考えます。

    • この未知の真の速度場 u_t(x) を、ニューラルネットワーク u_t^\theta(x) で近似することを目指します。

    • 学習は、回帰問題として定式化されます。つまり、ある損失関数（通常は二乗誤差）を用いて、u_t^\theta(X_t) が真の u_t(X_t) に近づくようにパラメータ \theta を最適化します。

      \mathcal{L}_{FM}(\theta) = \mathbb{E}_{t, X_t \sim p_t} [\| u_t^\theta(X_t) - u_t(X_t) \|^2] \tag{\text{原著 Eq. 2.4}}

    • しかし、周辺分布 p_t や真の周辺速度場 u_t(X_t) は通常、直接計算するのが困難です。

    • ここで巧妙なのは、「条件付きフローマッチング（Conditional Flow Matching, CFM）」という考え方です。学習データからランダムにターゲットサンプル X_1=x_1 を選び、この x_1 に条件付けられた確率パス p_{t|1}(x|x_1) と、それを生成する条件付き速度場 u_t(x|x_1) を考えます。

    • p_{t|1}(x|x_1) = \mathcal{N}(x|tx_1, (1-t)^2 I) の場合、このパスを生成する条件付き速度場は非常にシンプルに u_t(x|x_1) = \frac{x_1 - x}{1-t} となります（原著 Eq. 2.6）。

    • CFM損失は、この既知の条件付き速度場をターゲットとして回帰します。

      \mathcal{L}_{CFM}(\theta) = \mathbb{E}_{t, X_0 \sim p_0, X_1 \sim q} [\| u_t^\theta(X_t) - u_t(X_t|X_1) \|^2]

      ここで、X_t = (1-t)X_0 + tX_1 です。
      最も単純な線形パス X_t = (1-t)X_0 + tX_1 で、ターゲット X_1 のみに条件付けられた場合、サンプルは X_t = (1-t)X_0 + t x_1 となり、これを生成する条件付き速度場 u_t(X_t|x_1) は x_1 - X_0 となります (原著 Eq. 2.9)。このとき損失は

      \mathcal{L}_{OT,Gauss CFM}(\theta) = \mathbb{E}_{t \sim U[0,1], X_0 \sim \mathcal{N}(0,I), X_1 \sim q} [\| u_t^\theta((1-t)X_0+tX_1) - (X_1 - X_0) \|^2]

      となります。

    • 驚くべきことに、このCFM損失で学習しても、その勾配は元のFM損失の勾配と一致し（原著 §4.5 Theorem 4）、結果としてモデル u_t^\theta(x) は真の周辺速度場 u_t(x) を学習することが示されています。

1.2.1 サンプリング

学習後、新しいサンプルを生成するには、

  1. ソース分布 p_0 から初期サンプル X_0 をドローします。
  2. 学習された速度場 u_t^\theta(X_t) を用いて、ODE \frac{dX_t}{dt} = u_t^\theta(X_t) を t=0 から t=1 まで数値的に解きます。
  3. 最終的に得られた X_1 が、ターゲット分布 q からの新しいサンプルとなります。

この2ステップのアプローチ（パス設計と速度場回帰）が、フローマッチングの基本的な枠組みです。

1.3 なぜ「流れ」を学習するのか？その直感

フローマッチングは、データ空間内での確率分布の「地形」を変形させていく様子を捉えようとします。
ソース分布（例えば、一様に広がったノイズの「平原」）から、ターゲット分布（例えば、特定の形状を持つデータの「山脈」）へと、確率の塊を滑らかに「輸送」するイメージです。

  • 確率パス p_t(x): 時刻 t における確率分布の「スナップショット」です。t=0 の平原から t=1 の山脈へと、地形が徐々に変化していく様子を表します。
  • 速度場 u_t(x): 各地点 x における確率の「流れの速さと向き」を示します。この流れに従って確率の塊が動くことで、分布 p_t(x) が時間とともに変化していきます。

フローマッチングが学習するのは、この「流れのルール」そのものです。ルールさえ学習してしまえば、どんな初期状態（ソースサンプル）からでも、ルールに従って流れに乗せることで、最終的な目的地（ターゲットサンプル）に到達できる、というわけです。

拡散モデルでは、ノイズを徐々に加えていく固定の「拡散流」と、それを逆向きに辿る学習可能な「生成流」を考えていました。フローマッチングは、この「流れ」の概念をより一般化し、ソースとターゲットを直接結びつける流れを設計・学習することで、より効率的で表現力の高い生成モデリングを目指しています。

1.4 この章のまとめ：フローマッチングへの期待

この章では、フローマッチングの基本的な考え方と、その魅力について紹介しました。

  • フローマッチングは、ソース分布からターゲット分布への連続的な変換（フロー）を学習するフレームワークです。
  • このフローはODEによって記述され、そのODEを駆動する速度場をニューラルネットワークで学習します。
  • 拡散モデルの一般化と見なすことができ、シミュレーションフリーな学習や設計の柔軟性といった利点があります。
  • 基本的なレシピは、(1) 確率パスの設計、(2) 速度場の回帰学習、の2ステップです。
  • 条件付きフローマッチング損失を用いることで、ターゲットとなる速度場を容易に得られ、効率的な学習が可能です。

フローマッチングは、確率分布間の「最適な輸送経路」を見つけ出す最適輸送の理論とも深く関連しており、その数学的な美しさと実用的なパワフルさから、今後の生成AI分野でのさらなる発展が期待されています。

次章では、この「フロー」や「速度場」といった概念をより厳密に理解するために必要な数学的基礎（ODE、プッシュフォワード、連続の方程式など）を整理します。これらの道具立てを身につけることで、フローマッチングの核心的なメカニズムへと踏み込んでいく準備が整います。

ここまでの議論のポイント：

  • フローマッチング(FM)は、ソース分布からターゲット分布への連続的な「流れ」を学習する。
  • 流れはODEで記述され、その速度場をニューラルネットでモデル化する。
  • 拡散モデルの一般化と見なせ、シミュレーションフリー学習や柔軟なパス設計が利点。
  • 主要なステップは「確率パス設計」と「速度場回帰」。
  • 条件付きFM損失により、ターゲット速度場が簡単に得られ、効率的に学習できる。

第2章 フローの数理：フローマッチングの基礎を固める

この章のゴール：
この章では、フローマッチングの理論を理解し、実際にモデルを構築するために不可欠な数学的な概念を整理します。第1章で直感的に触れた「フロー（流れ）」や「速度場」が、どのように確率分布のダイナミクスを記述するのかを、常微分方程式（ODE）、プッシュフォワード写像、連続の方程式といった道具立てを通して見ていきます。また、フローモデルの学習における伝統的な課題であった尤度計算やシミュレーションコストについても触れ、フローマッチングがこれらの課題にどのようにアプローチするのか、その動機を明らかにします。この章を学ぶことで、フローマッチングがどのような数学的基盤の上に成り立っているのかを深く理解し、第3章以降の核心的な議論へと進むための強固な土台を築くことを目指します。

（原著の §3 "Flow models" に相当する内容です。）

2.1 フローモデルとは何か？：ODEによる決定論的変換

フローマッチングの「フロー（流れ）」は、数学的には時間依存の可逆な変換として定義されます。具体的には、ある d次元ユークリッド空間 \mathbb{R}^d 上の点 x が、時間 t \in [0,1] とともに動いていく様子を考えます。この動きは、時間依存の速度場（ベクトル場） u(t, x): [0,1] \times \mathbb{R}^d \to \mathbb{R}^d によって駆動される以下の常微分方程式（ODE）に従うとします。

\frac{dz(t)}{dt} = u(t, z(t)) \tag{\text{原著 Eq. 3.19a}}

初期条件を z(0) = x_0 とすると、このODEの解 z(t) は、時刻 0 での点 x_0 が時刻 t でどの位置 z(t) に移動するかを示します。この写像 x_0 \mapsto z(t) を \psi_t(x_0) と書くと、\psi_t: \mathbb{R}^d \to \mathbb{R}^d は時刻 t におけるフロー（流れ）を表します。つまり、\psi_t(x_0) は、初期点 x_0 から出発して、速度場 u に従って時刻 t まで流された結果の点です。定義より、\psi_0(x_0) = x_0（恒等写像）です。


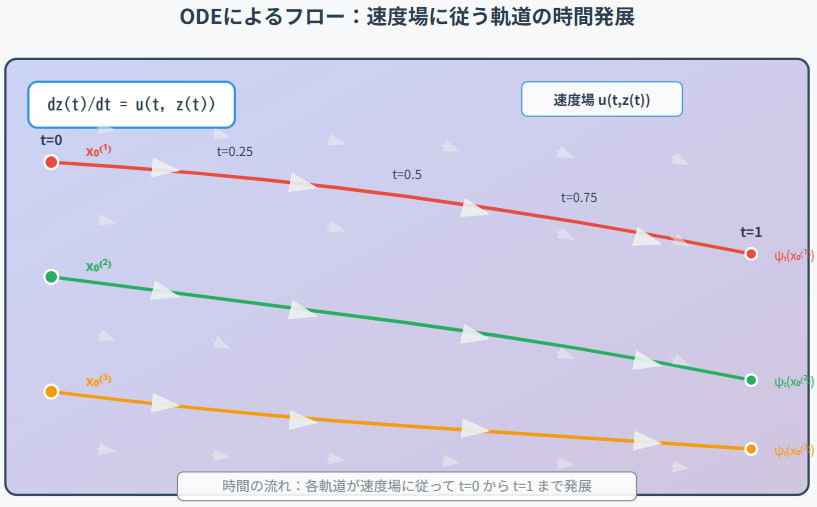
図2.1：ODEによるフローの概念図。初期点 x_0 が速度場 u(t, z(t)) に従って流れ、時刻 t で点 \psi_t(x_0) に到達する。異なる初期点（点線）は異なる経路を辿る。

フローの重要な性質：

  • 可逆性（Invertibility）: 速度場 u(t, x) が適切な滑らかさの条件（例えば、リプシッツ連続性）を満たせば、フロー \psi_t は各時刻 t で微分同相写像（diffeomorphism）となります。これは、\psi_t が滑らかで、かつ滑らかな逆写像 \psi_t^{-1} を持つことを意味します。つまり、時刻 t の状態 z(t) から時刻 0 の状態 x_0 へと一意に遡ることができます。
  • 決定論性（Determinism）: ODE (原著 Eq. 3.19a) は確率的な要素を含まないため、初期値 x_0 が決まれば、その後の軌道 \psi_t(x_0) は一意に定まります。これは拡散モデルでSDEを扱った点と対照的です（ただし、拡散モデルの確率フローODEは決定論的でした）。

フローマッチングでは、ソース分布 p_0 に従うサンプル X_0 を、このフロー \psi_t を用いて変換し、X_t = \psi_t(X_0) とします。目標は、X_1 = \psi_1(X_0) がターゲット分布 p_1 に従うように、速度場 u(t, x)（実際にはこれをパラメータ化したニューラルネットワーク u_t^\theta(x)）を学習することです。

2.1.1 速度場とフローの等価性 (原著 §3.4.1)

速度場 u(t, x) が与えられれば、ODE (原著 Eq. 3.19a) を解くことでフロー \psi_t(x) が一意に定まります（解の存在と一意性には u に関する条件が必要。原著 Theorem 1）。
逆に、可逆なフロー \psi_t(x) が与えられれば、それを生成する速度場 u(t, x) も一意に定まります。具体的には、\frac{d}{dt}\psi_t(x_0) = u(t, \psi_t(x_0)) の関係から、時刻 t と位置 x = \psi_t(x_0) における速度は、

u(t, x) = \dot{\psi}_t(\psi_t^{-1}(x)) \tag{\text{原著 Eq. 3.20}}

と書けます。ここで \dot{\psi}_t は \psi_t の時間微分です。
このように、速度場とフローは1対1に対応し、どちらかを指定すればもう一方が決まります。フローマッチングでは、学習の対象として速度場 u(t, x) をパラメータ化します。

2.2 プッシュフォワード：フローによる確率分布の変換

フロー \psi_t は個々のデータ点を変換しますが、我々が最終的に関心があるのは確率分布全体の変換です。
ソース分布 p_0(X_0) に従うランダム変数 X_0 がフロー \psi_t によって X_t = \psi_t(X_0) に変換されるとき、X_t が従う分布 p_t(X_t) はどうなるでしょうか？

p_t は、p_0 をフロー \psi_t で「押し出した」分布と考えられ、これを「プッシュフォワード測度（Pushforward Measure）」と呼び、p_t = (\psi_t)_{\#} p_0 と書きます。
X_t = x となる確率密度 p_t(x) は、変数変換の公式から以下のように与えられます（原著 §3.3 Eq. 3.14）。

p_t(x) = p_0(\psi_t^{-1}(x)) \left| \det J_{\psi_t^{-1}}(x) \right| \tag{\text{原著 Eq. 3.14}}

ここで、

  • \psi_t^{-1}(x) はフローの逆写像。
  • J_{\psi_t^{-1}}(x) は \psi_t^{-1} のヤコビ行列（x に関する偏導関数からなる行列）。
  • \det J_{\psi_t^{-1}}(x) はその行列式。
  • |\cdot| は絶対値。

この式は、点 x での確率密度 p_t(x) が、フローによって x に写ってくる元の点 \psi_t^{-1}(x) での確率密度 p_0(\psi_t^{-1}(x)) に、体積変化の補正項（ヤコビアンの行列式）を掛けたものになることを意味しています。


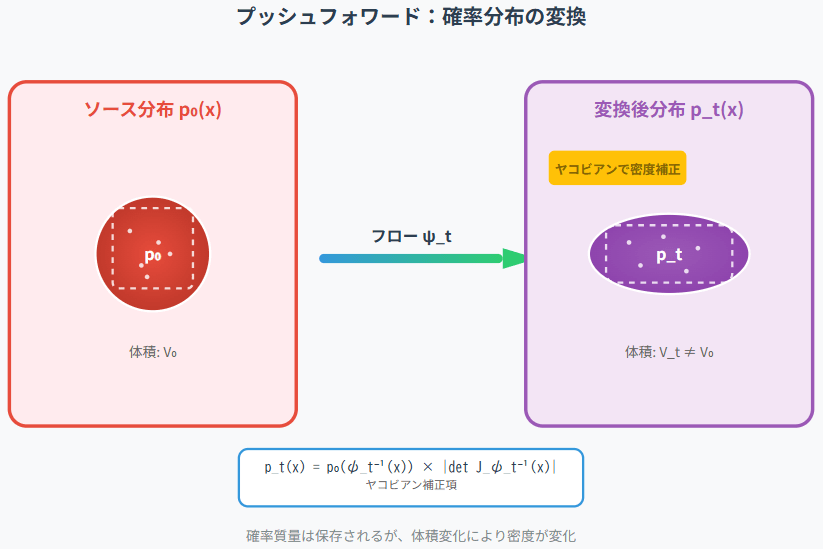
図2.2：プッシュフォワードの概念図。ソース分布 p_0（左）がフロー \psi_t によってターゲット分布 p_t（右）に変換される。ある領域の確率質量は保存されるが、体積が変化するため密度はヤコビアンで補正される。

2.3 確率パスと連続の方程式 (原著 §3.5)

フローマッチングでは、ソース分布 p_0 とターゲット分布 p_1 を結ぶ、時間的に連続な分布の列 p_t(x) を「確率パス（Probability Path）」と呼びます。この確率パスが、速度場 u(t, x) によって生成されるとは、X_t = \psi_t(X_0) （ただし X_0 \sim p_0）が分布 p_t に従うことを意味します（t \in [0,1) の範囲で。t=1 を除くのは、ターゲット分布 p_1 がコンパクトな台を持つ場合など、速度場が t=1 で定義されないケースを許容するためです。原著 Eq. 3.24）。

ある速度場 u(t, x) が確率パス p_t(x) を生成するかどうかを判定するための重要な関係式が「連続の方程式（Continuity Equation）」です。これは、確率の保存則を表す偏微分方程式（PDE）です（原著 Eq. 3.25）。

\frac{\partial p_t(x)}{\partial t} + \nabla_x \cdot (p_t(x) u(t, x)) = 0 \tag{\text{原著 Eq. 3.25}}

ここで、

  • \frac{\partial p_t(x)}{\partial t} は時刻 t における確率密度 p_t(x) の時間変化率。
  • \nabla_x \cdot (\cdot) はベクトル場の発散（divergence）で、\nabla_x \cdot v = \sum_j \frac{\partial v_j}{\partial x_j}。
  • p_t(x) u(t, x) は「確率流束（probability flux）」と呼ばれ、点 x を単位時間に通過する確率の流れの密度と方向を表します。

連続の方程式は、ある微小体積内の確率の時間変化が、その体積から流れ出す（または流れ込む）確率流束の正味の量に等しいことを述べています。

定理（質量保存則、原著 Theorem 2）:
確率パス p_t と（局所リプシッツかつ可積分な）速度場 u_t について、以下の2つは同値です。

  1. 連続の方程式 (原著 Eq. 3.25) が t \in [0,1) で成り立つ。
  2. 速度場 u_t が確率パス p_t を生成する（原著 Eq. 3.24 の意味で）。

この定理は、フローマッチングの理論的基盤となります。我々が設計した確率パス p_t があれば、それを連続の方程式に代入することで、対応する速度場 u_t を（原理的には）求めることができます。しかし、このPDEを直接解くのは一般に困難です。フローマッチングでは、より扱いやすい方法で u_t を見つけ出すアプローチを取ります（第3章）。

2.4 瞬間的変数変換と尤度計算 (原著 §3.6)

フローモデルの魅力の一つは、尤度 p_1(x_1) を正確に計算できる可能性があることです。これは、フロー \psi_t が可逆であるため、変数変換の公式を「瞬間的」に適用することで実現されます。
時刻 t におけるフロー \psi_t(x_0) に沿った対数尤度 \log p_t(\psi_t(x_0)) の時間変化は、以下のように書けます（原著 Eq. 3.30。これはInstantaneous Change of Variables formulaとして知られています）。

\frac{d}{dt} \log p_t(\psi_t(x_0)) = - \nabla_x \cdot u(t, \psi_t(x_0)) \tag{\text{原著 Eq. 3.30}}

この式の右辺は、フローの経路上での速度場の発散です。
このODEを t=0 から t=1 まで積分すると、ターゲット分布の対数尤度 \log p_1(\psi_1(x_0)) は、ソース分布の対数尤度 \log p_0(\psi_0(x_0)) = \log p_0(x_0) と、積分経路上での発散の総和として表すことができます（原著 Eq. 3.31）。

\log p_1(\psi_1(x_0)) = \log p_0(x_0) - \int_0^1 \nabla_x \cdot u(t, \psi_t(x_0)) dt \tag{\text{原著 Eq. 3.31}}

この式は、連続正規化フロー（CNF）の尤度計算式と同じです。
もし、速度場 u(t, x)（またはそのモデル u_t^\theta(x)）とその発散 \nabla_x \cdot u(t, x) が計算可能であれば、

  1. ターゲットサンプル x_1 を用意する。
  2. ODE \frac{dz(t)}{dt} = u(t, z(t)) を時刻 t=1 から t=0 へと逆向きに解き、z(1)=x_1 に対応するソースサンプル x_0 = z(0) を求める。
  3. その逆向きの軌道に沿って \int_1^0 \nabla_x \cdot u(t, z(t)) dt = - \int_0^1 \nabla_x \cdot u(t, z(t)) dt を計算する。
  4. \log p_1(x_1) = \log p_0(x_0) + \int_1^0 \nabla_x \cdot u(t, z(t)) dt として尤度が得られる。

2.4.1 従来のフローモデル学習の課題 (原著 §3.7)

この尤度計算 (原著 Eq. 3.31) は理論的には美しいですが、実際の学習に用いるにはいくつかの課題がありました。

  1. 発散計算のコスト: 高次元データの場合、\nabla_x \cdot u(t, x) (ヤコビアンのトレース) の計算コストが非常に大きくなります。Hutchinsonのトレース推定量など、不偏推定量を用いる方法がありますが、それでも計算負荷は高いです。
  2. ODEシミュレーションのコスト: 学習の各イテレーションで尤度を計算するために、(順方向または逆方向の) ODEを解く必要があり、これが学習全体の計算量を増大させます。

これらの課題のため、従来のCNFの学習は、最尤推定であっても計算コストが高いものでした。
フローマッチングは、このシミュレーションや発散計算を学習時には不要にする（または大幅に簡略化する）ことで、よりスケーラブルなフローモデルの学習を目指します。

2.5 この章のまとめ：フローマッチングを支える数学的道具

この章では、フローマッチングの理論的背景となるフローモデルの数学的な基礎を学びました。

  • フローモデル: 時間依存の速度場 u(t, x) によって駆動されるODE \frac{dz(t)}{dt} = u(t, z(t)) の解 \psi_t(x_0) として定義される、可逆で決定論的な変換です。
  • プッシュフォワード: フロー \psi_t は、ソース分布 p_0 をターゲット分布 p_t = (\psi_t)_{\#} p_0 へと変換します。その密度はヤコビアンで補正されます。
  • 確率パスと連続の方程式: ソース分布 p_0 とターゲット分布 p_1 を結ぶ時間連続な分布の列 p_t は、速度場 u_t と連続の方程式 \frac{\partial p_t}{\partial t} + \nabla \cdot (p_t u_t) = 0 で関連付けられます。
  • 瞬間的変数変換: フローに沿った対数尤度の変化は、速度場の発散で記述され、これによりターゲット尤度の正確な計算が（原理的には）可能です。
  • 従来の課題: 尤度計算のための発散計算とODEシミュレーションはコストが高く、スケーラブルな学習の妨げとなっていました。

これらの数学的基盤と課題認識の上に、フローマッチングは「シミュレーションフリー」かつ「発散計算フリー（多くの場合）」な学習を実現する新しいアプローチを提案します。次章では、いよいよフローマッチングの核心的なアルゴリズムとその理論的保証について詳しく見ていきます。

ここまでの議論のポイント：

  • フローはODEで定義される可逆な決定論的変換。速度場と1対1対応。
  • プッシュフォワードで確率分布がフローに従って変換される。
  • 確率パス p_t と速度場 u_t は連続の方程式で結ばれる。
  • フローモデルは原理的に正確な尤度計算が可能だが、発散計算とODEシミュレーションが学習時のボトルネックだった。
  • フローマッチングはこれらのボトルネックを回避することを目指す。

第3章 フローマッチングの核心：理論とアルゴリズム

この章のゴール：
この章では、フローマッチング（FM）の心臓部である学習アルゴリズムとその理論的な正当性に深く踏み込みます。第1章で概観した「確率パスの設計」と「速度場の回帰学習」という2つのステップが、具体的にどのように実現されるのかを詳細に解説します。特に、なぜ単純な条件付きフローマッチング（CFM）損失で学習したモデルが、複雑な周辺速度場を正しく捉えることができるのか、その鍵となる「周辺化トリック（Marginalization Trick）」を理解することが重要です。また、損失関数として用いられるBregmanダイバージェンスの役割や、様々なデータ結合（カップリング）の概念にも触れ、フローマッチングの柔軟性と一般性を示します。この章を通じて、フローマッチングがどのようにして効率的かつ効果的な生成モデルの学習を可能にするのか、その数学的な仕組みを明らかにします。

（原著の §4 "Flow Matching" の内容に相当する内容です。）

まず、この章で議論するフローマッチングのフレームワークにおける主要な構成要素とその間の関係性を、図3.0に示します。この図は、フロー、速度場、確率パス、境界条件、そして様々な損失関数がどのように連携してフローマッチングを実現するかを俯瞰するものです。特に、複雑な周辺フローの構築（図上段）を、より扱いやすい条件付きフロー（図中段）に分解し、それを学習するというフローマッチングの核心的な戦略（青い矢印で示される関係性）に注目してください。本章の議論を通じて、この図の各要素がどのように機能するのかを明らかにしていきます。


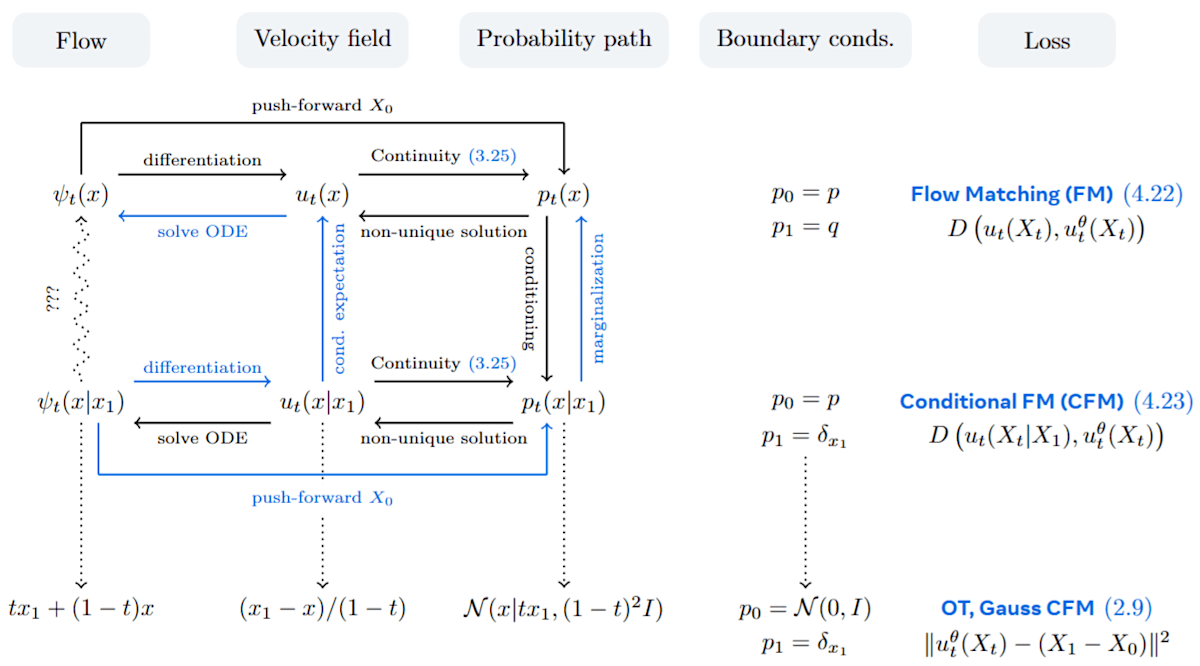
図3.0 (論文Figure 9)：フローマッチングフレームワークの主要なオブジェクトとその関係性。フローは速度場によって表現され、確率パスを生成するランダムプロセスを定義する。フローマッチングの主なアイデアは、望ましい境界条件（上段）を満たす複雑なフローの構築を、より単純な境界条件を満たし、結果として解くのが容易な条件付きフロー（中段）に分解することである。矢印は異なるオブジェクト間の依存関係を示し、青い矢印はフローマッチングフレームワークで利用される関係性を示す。損失列は速度場を学習するための損失をリストしており、CFM損失（中段と下段）が実際に用いられる。下段はセクション2（本記事の第1章クイックツアー）で説明された最も単純なFMアルゴリズムの具体例をリストしている。(Meta AI "Flow Matching Guide and Code" Fig. 9 より引用)

3.1 データと確率パスの構築 (原著 §4.1, 4.2)

フローマッチングの出発点は、ソース分布 p_0（通常は既知の単純な分布、例：\mathcal{N}(0,I)）とターゲット分布 p_1=q（訓練データから得られる未知の分布）です。これら2つの分布を結ぶ時間連続な確率パス p_t(x) を設計する必要があります。図3.0の上段および中段の「Probability path」列がこれに対応します。

3.1.1 データ結合（カップリング）

確率パスを構築する際、ソースサンプル X_0 \sim p_0 とターゲットサンプル X_1 \sim p_1 の間の関係性をどう設定するかが重要になります。これを「データ結合（Data Coupling）」または単に「カップリング」と呼び、同時分布 \pi_{0,1}(X_0, X_1) で表されます（図3.0には陽に描かれていませんが、確率パスの設計に影響します）。

  • 独立カップリング: 最も単純なのは、X_0 と X_1 を独立にサンプリングする場合です。つまり、\pi_{0,1}(X_0, X_1) = p_0(X_0)p_1(X_1)。これは、ノイズから画像を生成するような、一般的な無条件生成タスクでよく用いられます。
  • 依存カップリング: X_0 と X_1 が何らかの関係を持つ場合です。例えば、画像超解像タスクでは、X_0 が低解像度画像、X_1 が対応する高解像度画像となります。あるいは、画像修復タスクでは、X_0 がマスクされた画像、X_1 が修復された完全な画像です。このような場合、データセット自体がペア (X_0, X_1) として与えられることが多いです。

フローマッチングの柔軟性の一つは、これらの異なるカップリングを自然に扱える点にあります。

3.1.2 条件付き確率パスの導入

周辺確率パス p_t(x) を直接設計し、それに対応する周辺速度場 u_t(x) を求めるのは依然として難しい問題です（図3.0上段）。そこでフローマッチングでは、より扱いやすい条件付き確率パス p_{t|z}(x|z) を導入します（図3.0中段）。これは、ある（一般には X_0 や X_1、あるいはその両方に関連する）条件変数 Z=z が与えられた下での、時刻 t における X_t の分布です。

周辺確率パス p_t(x) は、この条件付き確率パスを Z の分布 p_Z(z) で平均（周辺化、図3.0の "marginalization" 矢印）することで得られます。

p_t(x) = \int p_{t|z}(x|z) p_Z(z) dz \tag{\text{原著 Eq. 4.11}}

最も一般的なのは、Z=X_1 （ターゲットサンプルに条件付ける）または Z=(X_0, X_1) （ソースとターゲットのペアに条件付ける）というケースです。

原著の§4.2では、主に Z=X_1 の場合、つまり p_{t|1}(x|x_1) を考え、これを集約して p_t(x) を構築するアプローチが紹介されています。
この条件付き確率パス p_{t|1}(x|x_1) は、以下の境界条件（図3.0中段「Boundary conds.」列）を満たすように設計されます（原著 Eq. 4.6）。

  • t=0 で： p_{0|1}(x|x_1) = \pi_{0|1}(x|x_1) （X_0 の条件付き分布。独立カップリングなら p_0(x)）
  • t=1 で： p_{1|1}(x|x_1) = \delta_{x_1}(x) （x_1 に集中するデルタ関数）

これにより、周辺パス p_t(x) は自動的に p_0(x) から p_1(x) へと補間されます。
例えば、原著で紹介されている線形補間パス（条件付きガウスパス、原著 §2の例。図3.0下段の N(x|tx_1, (1-t)^2I)）は、この条件を満たす良い例です。
X_t = (1-t)X_0 + t X_1 の場合、X_0 \sim p_0 とすると、X_1=x_1 に条件づけたときの X_t の分布が p_{t|1}(x|x_1) になります。

3.2 生成速度場の導出 (原著 §4.3)

条件付き確率パス p_{t|1}(x|x_1) を設計したら、次にそれを生成する条件付き速度場 u_t(x|x_1) を見つける必要があります（図3.0中段「Velocity field」列）。
これは、第2章で見たように、条件付き確率パス p_{t|1}(x|x_1) と条件付き速度場 u_t(x|x_1) が、条件 x_1 を固定した上で連続の方程式（図3.0の "Continuity (3.25)" で示される関係）を満たすように定義されます。

\frac{\partial p_{t|1}(x|x_1)}{\partial t} + \nabla_x \cdot (p_{t|1}(x|x_1) u_t(x|x_1)) = 0

多くの場合、この条件付き速度場 u_t(x|x_1) は解析的に求めることができます。
例えば、確率変数 X_t が X_t = \phi_t(X_0|x_1) という形の条件付きフロー（X_0 \sim \pi_{0|1}(\cdot|x_1)）で与えられる場合（図3.0の "push-forward X_0" や "solve ODE" の関係）、u_t(x|x_1) = \dot{\phi}_t(\phi_t^{-1}(x|x_1)|x_1) となります（原著 §4.6.1 Eq. 4.31）。

第1章で触れた線形パス X_t = (1-t)X_0 + t x_1 (ここで X_0 \sim p_0(X_0) = \mathcal{N}(0,I)) の場合、
時刻 t でのサンプルは X_t = (1-t)X_0 + t x_1 です。
これを生成する X_0 から X_t への写像は \phi_t(X_0|x_1) = (1-t)X_0 + t x_1。
その時間微分 \dot{\phi}_t(X_0|x_1) = x_1 - X_0 です。
この速度場を X_t の関数として表すと、X_0 = (X_t - t x_1)/(1-t) なので、
u_t(X_t|x_1) = x_1 - \frac{X_t - t x_1}{1-t} = \frac{(1-t)x_1 - X_t + t x_1}{1-t} = \frac{x_1 - X_t}{1-t} となります (原著 Eq. 2.6、図3.0下段の (x_1-x)/(1-t))。これがターゲットとなる条件付き速度場です。


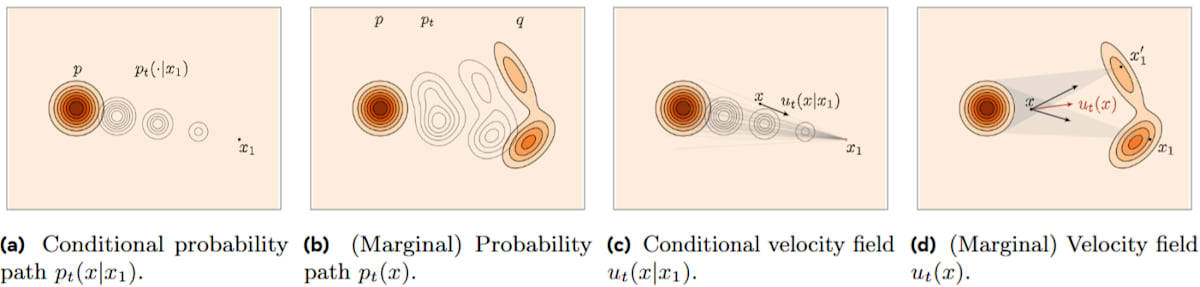
図3.1：フローマッチングにおけるパス設計。固定されたターゲットサンプル X=x_1 が与えられたとき、その条件付き速度場 u_t(x|x_1) が条件付き確率パス p_t(x|x_1) を生成する。周辺速度場 u_t(x) は、全ての条件付き速度場を集約した結果であり、同様に周辺確率パス p_t(x) を生成する。(Meta AI "Flow Matching Guide and Code" Fig. 3 より引用)

3.3 周辺化トリック：条件付きから周辺へ (原著 §4.4)

さて、我々が最終的に学習したいのは、周辺確率パス p_t(x) を生成する周辺速度場 u_t(x) です（図3.0上段）。
この周辺速度場 u_t(x) は、条件付き速度場 u_t(x|x_1) を事後分布 p_{1|t}(x_1|x) （時刻 t に x にいるという条件下で、ターゲットが x_1 であった確率）で平均することで得られます（図3.0の "cond. expectation" 矢印、原著 Eq. 4.8, 4.10）。

u_t(x) = \mathbb{E}_{X_1 \sim p_{1|t}(\cdot|x)} [u_t(x|X_1)] = \int u_t(x|x_1) p_{1|t}(x_1|x) dx_1

ここで、p_{1|t}(x_1|x) = \frac{p_{t|1}(x|x_1)q(x_1)}{p_t(x)} です（ベイズの定理、原著 Eq. 4.9）。

この u_t(x) は、多数の訓練サンプル x_1 にわたる積分を含むため、直接計算するのは困難です。
しかし、フローマッチングの素晴らしい点は、この複雑な周辺速度場 u_t(x) を直接ターゲットとしなくても、より単純な条件付き速度場 u_t(x|X_1) をターゲットとする条件付きフローマッチング（CFM）損失で学習すれば、結果的に周辺速度場 u_t(x) が学習されるという事実にあります。これを「周辺化トリック（Marginalization Trick）」と呼びます。

定理（周辺化トリック、原著 Theorem 3）:
（適切な正則性の仮定の下で）もし条件付き速度場 u_t(x|z) が条件付き確率パス p_{t|z}(x|z) を生成するならば、周辺速度場 u_t(x) = \mathbb{E}_{Z \sim p_{Z|t}(\cdot|x)} [u_t(x|Z)] は周辺確率パス p_t(x) = \int p_{t|z}(x|z)p_Z(z)dz を生成する。
（ここで z は一般的な条件変数。Z=X_1 とすれば上記に対応。）

この定理により、我々は単純な条件付きオブジェクト p_{t|z}(x|z) と u_t(x|z) を設計・計算し、それらを使って学習するだけで、望ましい周辺オブジェクト p_t(x) と u_t(x) を暗黙的に実現できることが保証されます。図3.0で言えば、中段の要素を設計・利用することで、上段の要素を（シミュレーションフリーで）学習できるということです。

3.4 フローマッチング損失 (原著 §4.5)

学習の目標は、ニューラルネットワークでパラメータ化された速度場 u_t^\theta(x) が、真の（周辺）速度場 u_t(x) に近づくようにすることです。
これは、Bregmanダイバージェンス D(\cdot, \cdot) を用いた以下のフローマッチング（FM）損失で定式化されます（図3.0上段「Loss」列）。

\mathcal{L}_{FM}(\theta) = \mathbb{E}_{t \sim U[0,1], X_t \sim p_t} [ D(u_t(X_t), u_t^\theta(X_t)) ] \tag{\text{原著 Eq. 4.2, 4.22}}

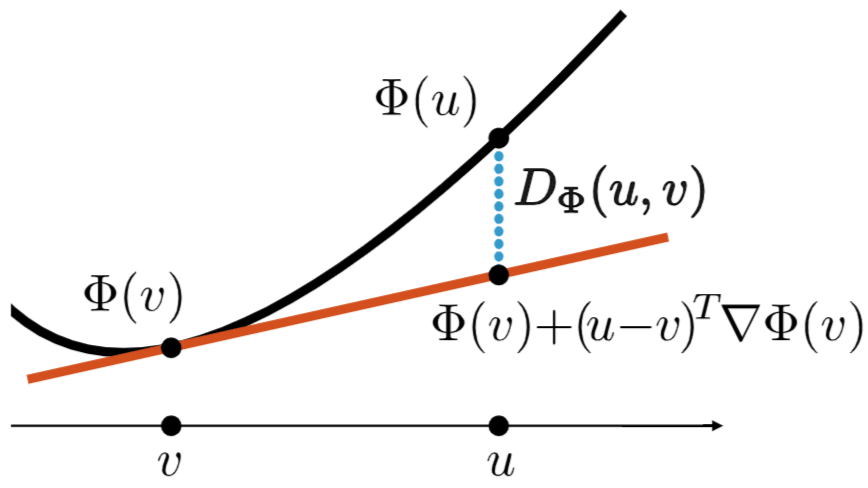
Bregmanダイバージェンスは、\Phi を狭義凸関数としたとき D(u,v) = \Phi(u) - \Phi(v) - \langle \nabla\Phi(v), u-v \rangle で定義される非対称な「距離」のようなものです。最も一般的なのは、\Phi(u) = \|u\|^2/2 とした場合の二乗誤差 D(u,v) = \frac{1}{2}\|u-v\|^2 です。


図3.2：Bregmanダイバージェンス。D(u,v) は、\Phi(u) と、\Phi(v) 周りでの \Phi の線形近似を u で評価した値との差として定義される。(Meta AI "Flow Matching Guide and Code" Fig. 10 より引用)

しかし、前述の通り u_t(X_t) は扱いづらいです。そこで、条件付きフローマッチング（CFM）損失を考えます（図3.0中段「Loss」列）。

\mathcal{L}_{CFM}(\theta) = \mathbb{E}_{t \sim U[0,1], Z \sim p_Z, X_t \sim p_{t|Z}(\cdot|Z)} [ D(u_t(X_t|Z), u_t^\theta(X_t)) ] \tag{\text{原著 Eq. 4.23}}

ここで、u_t(X_t|Z) は既知の（または容易に計算可能な）ターゲットとなる条件付き速度場です。
Z=X_1 で、二乗誤差を用いる場合、

\mathcal{L}_{CFM}(\theta) = \mathbb{E}_{t, X_0 \sim p_0, X_1 \sim q} [ \| u_t( (1-t)X_0+tX_1 | X_1) - u_t^\theta((1-t)X_0+tX_1) \|^2 ]

となります（サンプル X_t の生成方法は確率パスの設計に依存します）。
図3.0の下段「Loss」列に示される「OT, Gauss CFM」損失 \|u_t^\theta(X_t) - (X_1-X_0)\|^2 は、線形パス X_t = (1-t)X_0 + tX_1 で、X_0 に条件付けた速度場 X_1-X_0 をターゲットとする、非常にシンプルなCFM損失の一例です。

定理（FM損失とCFM損失の勾配の等価性、原著 Theorem 4）:
Bregmanダイバージェンス D の（第2引数に関する）勾配がアフィン不変性を持つという重要な性質（原著 Eq. 4.20, 4.21）により、

\nabla_\theta \mathcal{L}_{FM}(\theta) = \nabla_\theta \mathcal{L}_{CFM}(\theta)

が成り立ちます。つまり、CFM損失を最小化することは、FM損失を最小化することと（勾配の観点から）等価です。
さらに、CFM損失の最小解は、周辺速度場 u_t^\theta(x) = \mathbb{E}_{Z \sim p_{Z|t}(\cdot|x)} [u_t(x|Z)] を与えます。

この定理が、フローマッチングの学習を実用的なものにするための核心的な結果です。我々は、扱いやすい条件付き量をターゲットにして回帰学習を行うだけで、目的の複雑な周辺量を学習できるのです。

（原著 Proposition 1 は、この勾配等価性のより一般的な形を示しています。）

3.5 条件付きフローによる条件付き生成 (原著 §4.6)

これまで、条件変数 Z を使って周辺パス p_t(x) と周辺速度場 u_t(x) を構築する話をしてきました。この枠組みを、より直接的に「条件付き生成 p_t(x|y)」に応用することもできます。
例えば、テキスト記述 y に基づいて画像 x を生成したい場合、学習データは (x_1, y) のペアで与えられます。
このとき、確率パス p_t(x|y) を、

  • p_{0|y}(x|y) = p_0(x) （ソースは条件 y に依存しないノイズ）
  • p_{1|y}(x|y) = q(x|y) （ターゲットは条件 y に従うデータ分布）
    となるように設計します。

そして、学習時には、u_t^\theta(X_t, y) という条件 y も入力に取る速度場モデルを考え、CFM損失

\mathcal{L}_{CFM,cond}(\theta) = \mathbb{E}_{t, (X_1,Y) \sim q(\cdot,\cdot), X_0 \sim p_0} [ \| u_t(X_t|X_1,Y) - u_t^\theta(X_t, Y) \|^2 ]

（ここで X_t は X_0, X_1, Y から定まる）のような形で学習します。
サンプリング時には、所望の条件 Y=y を u_t^\theta(X_t, y) に与えてODEを解けば、q(x|y) からのサンプルが得られます。
（これは、第4章で見た拡散モデルの分類器無しガイダンスと似た構造を、より一般的に実現する方法と言えます。）

原著の§4.6では、Z=X_1 の場合の条件付きフロー \psi_t(X_0|x_1)（図3.0中段「Flow」列）を導入し、それから条件付き速度場 u_t(x|x_1) = \dot{\psi}_t(\psi_t^{-1}(x|x_1)|x_1) （図3.0の "differentiation" 矢印）を導き、CFM損失を再訪しています。
これは、確率パス p_{t|1}(x|x_1) を明示的に定義する代わりに、それを生成する決定論的な（条件付き）フロー \psi_t(X_0|x_1) を定義することで、対応する条件付き速度場を導出する方法です。このフローは、

  • \psi_0(X_0|x_1) = X_0
  • \psi_1(X_0|x_1) = x_1
    を満たすように設計されます（原著 Eq. 4.29）。この設計の自由度がフローマッチングの強みの一つです。

3.5.1 様々な条件付けの選択肢 (原著 §4.6.3, Fig. 11)


図3.3：フローマッチングにおける様々な条件付け形式と対応する条件付きフロー。左から、X_1 条件付け、 X_0 条件付け、 (X_0, X_1) 条件付け。条件付きフローが微分同相写像であれば、これらは全て等価な周辺速度場と周辺確率パスを導く。(Meta AI "Flow Matching Guide and Code" Fig. 11 より引用)

条件変数 Z の選び方にはいくつかのバリエーションがあります。

  • Z=X_1 (ターゲット条件付け): これまで主に見てきたケースです。\psi_t(X_0|X_1) や u_t(X_t|X_1) を考えます。
  • Z=X_0 (ソース条件付け): X_0 を固定し、X_1 へと向かうフロー \psi_t(X_1|X_0) や u_t(X_t|X_0) を考えます。これは、例えば画像編集タスク（ソース画像 X_0 を編集後のターゲット X_1 へ変換）などで有用です。
  • Z=(X_0,X_1) (ペア条件付け): ソースとターゲットのペア (X_0,X_1) を固定し、それらを補間するフロー \psi_t(X_0,X_1) （これは時刻 t のサンプル X_t そのものを指すことが多い）や、その時間微分 \dot{\psi}_t(X_0,X_1) を速度場とします。この場合、速度場は X_t に陽に依存せず、X_0, X_1, t の関数となります。これは「確率的補間（Stochastic Interpolant）」の考え方と密接に関連します。

重要なのは、これらの条件付きフローが適切に（例えば微分同相写像として）定義されれば、周辺化トリックによって、最終的に得られる周辺速度場 u_t(x) と周辺確率パス p_t(x) は理論上同じものになるということです。ただし、学習のしやすさや数値的安定性は選択に依存する可能性があります。

3.6 最適輸送と線形条件付きフロー (原著 §4.7)

条件付きフロー \psi_t(X_0|x_1) をどのように設計するかが、フローマッチングの性能に影響します。一つの理想的な指標として「最適輸送（Optimal Transport, OT）」の概念があります。
動的OT問題は、あるコスト（例えば、移動する「運動エネルギー」\int_0^1 \|u_t(X_t)\|^2 dt）を最小化するように、ソース分布 p_0 をターゲット分布 p_1 へと輸送するフローを見つける問題です（原著 Eq. 4.41）。
二次コストの場合、この解は「OT変位補間（OT displacement interpolant）」と呼ばれ、X_t = (1-t)X_0 + t \phi(X_0) の形をします。ここで \phi: \mathbb{R}^d \to \mathbb{R}^d はOT写像です。この経路は、サンプルが「まっすぐ」ターゲットに向かうことを促します。

フローマッチングでは、このOTのアイデアを条件付きフローに取り入れます。
具体的には、CFM損失の上界を最小化するような条件付きフローを考えると、それは線形条件付きフロー

\psi_t(x_0|x_1) = (1-t)x_0 + t x_1 \tag{\text{原著 Eq. 4.48}}

であることが示されます（Liu et al., 2022; Lipman et al., 2022）。
このとき、対応する条件付き速度場は（X_0 を入力とすると） \dot{\psi}_t(X_0|x_1) = X_1 - X_0 となり、CFM損失は

\mathcal{L}_{CFM,OT}(\theta) = \mathbb{E}_{t,X_0,X_1} [ \| (X_1 - X_0) - u_t^\theta((1-t)X_0+tX_1) \|^2 ] \tag{\text{原著 Eq. 2.9}}

となります。これが、第1章のクイックツアーで紹介された最も基本的なフローマッチング損失であり、図3.0の下段に示される「OT, Gauss CFM」の具体例です。
この「条件付きOTフロー」は、学習を安定させ、サンプリング時のODEステップ数を減らす効果が期待されます。

3.7 アフィン条件付きフローとその仲間たち (原著 §4.8)

線形条件付きフロー \psi_t(x_0|x_1) = (1-t)x_0 + t x_1 は、より一般的なアフィン条件付きフロー

\psi_t(x_0|x_1) = \sigma_t x_0 + \alpha_t x_1 \tag{\text{原著 Eq. 4.50}}

の特殊なケースです。ここで、\sigma_t, \alpha_t はスカラーの時間依存係数で、境界条件 \sigma_0=1, \alpha_0=0 および \sigma_1=0, \alpha_1=1 を満たし、かつ \alpha_t は単調増加、\sigma_t は単調減少するように設計されます（例：\sigma_t = 1-t, \alpha_t=t）。

このアフィン条件付きフローに対応する条件付き速度場は \dot{\psi}_t(X_0|X_1) = \dot{\sigma}_t X_0 + \dot{\alpha}_t X_1 です。
この速度場 u_t(x) (原著 Eq. 4.52)、ターゲット予測 x_{1|t}(x) = \mathbb{E}[X_1|X_t=x] (原著 Eq. 4.58)、ソース予測 x_{0|t}(x) = \mathbb{E}[X_0|X_t=x] (原著 Eq. 4.59) の間には線形な変換関係があり（原著 Table 1）、学習ターゲットとしてどれを選んでも理論上は等価です。これは拡散モデルにおけるノイズ予測とスコア予測の等価性に似ています。

3.7.1 ガウスパス (原著 §4.8.3)

特に重要なのは、ソース分布 p_0(x_0) = \mathcal{N}(x_0|0, \sigma^2 I) がガウス分布である場合です。図3.0の下段の確率パス N(x|tx_1, (1-t)^2I) はこの一例です。
このとき、アフィン条件付きフローから導かれる条件付き確率パス p_{t|1}(x|x_1) もガウス分布

p_{t|1}(x|x_1) = \mathcal{N}(x | \alpha_t x_1, \sigma_t^2 I) \tag{\text{原著 Eq. 4.70}}

となります。
これは、拡散モデルで用いられるノイズ付加過程と非常によく似た形をしています。
例えば、

  • Variance Preserving (VP) スケジューラ:
    \alpha_t = \sqrt{1-e^{-\beta_t}}, \sigma_t = e^{-\beta_t/2} のような形。
  • Variance Exploding (VE) スケジューラ:
    \alpha_t = 1, \sigma_t = \sigma_{\text{max}}(1-t) のような形。
    （ここで \sigma_{\text{max}} はソース分布のノイズレベルに関連する定数）
    あるいは、より一般的に \sigma_t は t=0 で大きな値をとり t=1 で 0 になる単調減少関数。

これらのガウスパスの場合、周辺スコア \nabla \log p_t(x) は、周辺速度場 u_t(x) と簡単な関係で結びつきます（原著 Eq. 4.79）。これにより、拡散モデルのスコアマッチングとフローマッチングの速度場学習が密接に関連付けられます。

3.8 この章のまとめ：フローマッチングの動作原理

この章では、フローマッチングの核心的な理論とアルゴリズムについて、図3.0のフレームワークを参照しながら学びました。

  • 確率パスは、扱いやすい条件付き確率パス p_{t|z}(x|z) とそれを生成する条件付き速度場 u_t(x|z) を設計し、それらを周辺化することで構築される。
  • 周辺化トリックにより、条件付き量をターゲットとしたCFM損失で学習すれば、目的の周辺速度場が学習されることが保証される。これはBregmanダイバージェンスの性質に由来する。
  • 条件付きフロー \psi_t(X_0|x_1) を設計することで、対応する条件付き速度場を導出できる。特に、最適輸送に動機付けられた線形条件付きフロー \psi_t(x_0|x_1) = (1-t)x_0 + t x_1 は、シンプルかつ効果的な選択肢である。
  • より一般的なアフィン条件付きフローや、ソースがガウス分布の場合のガウスパスは、拡散モデルとの繋がりを示唆する。

フローマッチングは、これらの理論的基盤の上に、多様なデータモダリティやタスクに対して柔軟かつ効果的に適用できる生成モデリングの枠組みを提供します。
次章以降では、この基本的なフローマッチングの考え方を、リーマン多様体上のような非ユークリッド空間や、離散データ空間へと拡張していく様子を見ていきます。

ここまでの議論のポイント：

  • 確率パスは条件付きパスとその速度場から構築。
  • 周辺化トリック：CFM損失で周辺速度場を学習可能。
  • 条件付きフローの設計が鍵。線形OTフローが基本。
  • アフィンフロー、ガウスパスは拡散モデルと関連。

第4章 フローマッチングの拡張(1)：多様体上の流れ

この章のゴール：
これまでの章では、主にユークリッド空間 \mathbb{R}^d 上でのフローマッチングを扱ってきました。しかし、現実世界のデータ、例えば地球上の気象データ（球面上）、タンパク質の構造（回転や平行移動の対称性を持つ空間）、あるいはロボットの関節角度（トーラス上）などは、ユークリッド空間では自然に表現できない複雑な幾何学的構造（多様体）を持っています。この章では、フローマッチングの強力な枠組みを、これらの非ユークリッド空間、特にリーマン多様体へと拡張する方法を探求します。多様体上の確率分布、フロー、速度場といった概念を導入し、ユークリッド空間でのフローマッチングのアイデアがどのように一般化されるのかを見ていきます。特に、多様体上の「まっすぐな」経路である測地線を用いた条件付きフローの構築や、より一般的なプレメトリック（premetric）を用いたフローの設計が鍵となります。この章を通じて、フローマッチングがいかにして複雑な幾何学的制約を持つデータを扱えるようになるのか、その理論と可能性を理解することを目指します。

（原著の §5 "Non-Euclidean Flow Matching" の内容に相当する内容です。）

4.1 リーマン多様体：曲がった空間の幾何学

まず、フローマッチングを拡張する先の舞台となる「リーマン多様体（Riemannian Manifold）」について簡単に触れておきましょう。

  • 多様体（Manifold）: 局所的にはユークリッド空間のように見える空間のことです。例えば、地球の表面（球面）は、我々の身の回りでは平らな2次元平面のように見えますが、大域的には曲がった2次元の多様体です。
  • リーマン計量（Riemannian Metric）: 多様体の各点にある「接空間（Tangent Space）」（その点で多様体に接するユークリッド空間のようなもの）上で、ベクトルの長さや角度を測るための「内積」を滑らかに定義したものです。このリーマン計量があることで、多様体上で曲線や距離、曲率といった幾何学的な量を考えることができます。
  • リーマン多様体: リーマン計量が備わった多様体のことです。

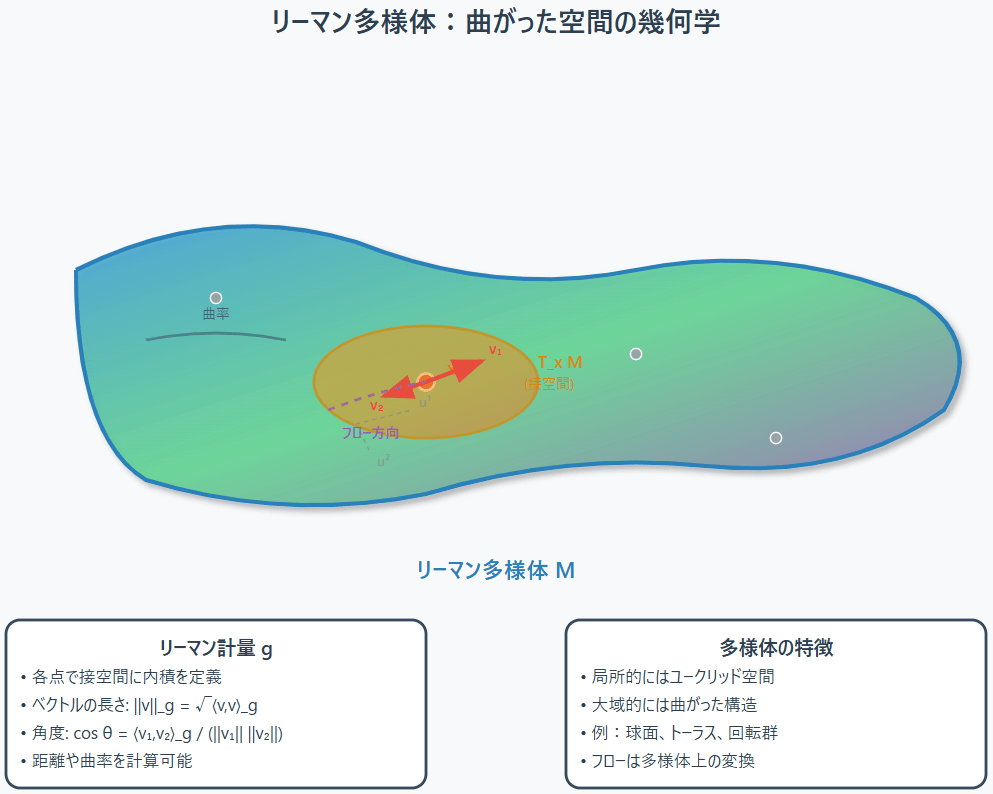
フローマッチングをリーマン多様体 \mathcal{M} に拡張するとは、ソース分布 p_0 とターゲット分布 p_1 が \mathcal{M} 上で定義され、それらを結ぶフロー \psi_t: \mathcal{M} \to \mathcal{M} も \mathcal{M} 上の変換として学習することを意味します。


図4.1：リーマン多様体のイメージ。局所的にはユークリッド的だが、大域的には曲がっている。各点には接空間 T_x\mathcal{M} が存在し、リーマン計量 g がそこで内積を定義する。

4.2 多様体上の確率、フロー、速度場 (原著 §5.1, 5.2)

ユークリッド空間での概念を多様体上に一般化します。

  • 確率密度: 多様体 \mathcal{M} 上の確率密度関数 p(x) は、x \in \mathcal{M} に対して非負の値を持ち、多様体全体での積分（体積要素 d\text{vol}_x を用いる）が1になる関数です: \int_{\mathcal{M}} p(x) d\text{vol}_x = 1。
  • フロー: 時間依存のフロー \psi_t: \mathcal{M} \to \mathcal{M} は、各時刻 t で多様体から多様体への微分同相写像です。
  • 速度場: 速度場 u_t(x) は、各点 x \in \mathcal{M} と時刻 t に対して、その点の接空間 T_x\mathcal{M} に属するベクトルを割り当てます。つまり、u_t(x) \in T_x\mathcal{M}。
    フロー \psi_t(x_0) は、多様体上のODE \frac{d\psi_t(x_0)}{dt} = u_t(\psi_t(x_0)) の解として定義されます（原著 Theorem 8 は、ユークリッド空間でのODEの解の存在と一意性の定理の多様体版です）。

4.2.1 多様体上の連続の方程式と瞬間的変数変換

第2章で見た連続の方程式や瞬間的変数変換の公式も、リーマン多様体上に自然に拡張されます。

  • リーマン連続の方程式 (原著 Eq. 5.1):
\frac{\partial p_t(x)}{\partial t} + \text{div}_g (p_t(x) u_t(x)) = 0 \tag{\text{原著 Eq. 5.1}}

ここで \text{div}_g はリーマン計量 g に関する発散演算子です。

  • リーマン瞬間的変数変換 (原著 Eq. 5.3):
\frac{d}{dt} \log p_t(\psi_t(x_0)) = - \text{div}_g (u_t(\psi_t(x_0))) \tag{\text{原著 Eq. 5.3}}

これらの式はユークリッド空間の場合と形式的には同じですが、発散演算子がリーマン計量を考慮したものに置き換わっています。
これにより、多様体上でもフローモデルの尤度計算や、速度場と確率パスの関係性を理論的に扱うことができます。

4.3 多様体上の確率パスと周辺化トリック (原著 §5.3, 5.4)

フローマッチングの核となる確率パスの構築と周辺化トリックも、リーマン多様体上に拡張できます。

  • 多様体上の確率パス (原著 Eq. 5.6):
    周辺確率パス p_t(x) は、条件付き確率パス p_{t|1}(x|x_1) （x, x_1 \in \mathcal{M}）をターゲット分布 q(x_1) で平均することで構築されます。
p_t(x) = \int_{\mathcal{M}} p_{t|1}(x|x_1) q(x_1) d\text{vol}_{x_1} \tag{\text{原著 Eq. 5.6}}

条件付きパスは、境界条件 p_{0|1}(x|x_1) = \pi_{0|1}(x|x_1) と p_{1|1}(x|x_1) = \delta_{x_1}(x) を満たすように設計されます（原著 Eq. 5.8）。

  • 多様体上の周辺化トリック (原著 Theorem 10):
    ユークリッド空間の場合と同様に、適切な正則性の仮定（原著 Assumption 2）のもとで、条件付き速度場 u_t(x|x_1) \in T_x\mathcal{M} が条件付きパス p_{t|1}(x|x_1) を生成するならば、周辺速度場 u_t(x) = \mathbb{E}_{X_1 \sim p_{1|t}(\cdot|x)} [u_t(x|X_1)] は周辺パス p_t(x) を生成します。

これにより、多様体上でも条件付き量をターゲットとした学習が正当化されます。

4.4 リーマンフローマッチング損失 (原著 §5.5)

学習に用いる損失関数も、多様体の構造を考慮したものになります。
リーマン条件付きフローマッチング（RCFM）損失は、各点 X_t \in \mathcal{M} の接空間 T_{X_t}\mathcal{M} 上で定義されるBregmanダイバージェンス D_{X_t}(\cdot, \cdot) を用いて、以下のように定義されます（原著 Eq. 5.13）。

\mathcal{L}_{RCFM}(\theta) = \mathbb{E}_{t, X_1 \sim q, X_t \sim p_{t|1}(\cdot|X_1)} [ D_{X_t}(u_t(X_t|X_1), u_t^\theta(X_t)) ] \tag{\text{原著 Eq. 5.13}}

ここで、u_t(X_t|X_1) と u_t^\theta(X_t) はともに X_t の接空間 T_{X_t}\mathcal{M} のベクトルです。Bregmanダイバージェンス D_{X_t} は、例えばリーマン計量 g から誘導される二乗ノルム \|v\|^2_g = \langle v, v \rangle_g を用いて、D_{X_t}(u,v) = \frac{1}{2}\|u-v\|^2_g と定義できます。

ユークリッド空間と同様に、このRCFM損失の勾配は、周辺量をターゲットとしたリーマンフローマッチング（RFM）損失の勾配と一致します（原著 Theorem 11）。

4.5 多様体上の条件付きフロー：測地線とプレメトリック (原著 §5.6)

フローマッチングの設計において重要なのは、扱いやすく、かつ効果的な条件付きフロー \psi_t(x_0|x_1) （x_0, x_1 \in \mathcal{M}）をどのように構築するかです。これは、対応する条件付き速度場 u_t(x|x_1) を決定します。

4.5.1 測地線フロー (Geodesic Flow)

リーマン多様体において、ユークリッド空間の「直線」に相当する概念が「測地線（Geodesic）」です。測地線は、2点間の最短経路（局所的には）を与えます。
この測地線を用いて、条件付きフローを構築することができます。
まず、多様体上の2点 x_0, x_1 を結ぶ（ユニークな、または主要な）測地線を考えます。

  • 指数写像 (Exponential Map) \exp_{x_0}: T_{x_0}\mathcal{M} \to \mathcal{M}: 点 x_0 の接空間内のベクトル v \in T_{x_0}\mathcal{M} を、初期速度 v で x_0 から出発する測地線に沿って時間1だけ進んだ先の点に写す写像です。
  • 対数写像 (Logarithmic Map) \log_{x_0}: \mathcal{M} \to T_{x_0}\mathcal{M}: 点 x_1 \in \mathcal{M} を、点 x_0 から x_1 へ向かう測地線の初期接ベクトルに写す写像です（指数写像の（局所的な）逆写像）。\log_{x_0}(x_1) は x_0 から x_1 への「方向と距離」を表すベクトルです。

これらを用いると、測地線条件付きフローは以下のように定義できます（原著 Eq. 5.17）。

\psi_t(x_0|x_1) = \exp_{x_0} (\kappa(t) \log_{x_0}(x_1)) \tag{\text{原著 Eq. 5.17}}

ここで、\kappa(t): [0,1] \to [0,1] は単調増加するスケジューリング関数で、\kappa(0)=0, \kappa(1)=1 を満たします。
これは、x_0 から x_1 へ向かう測地線上の経路を、時間パラメータ \kappa(t) に従って進むことを意味します。

  • t=0 (\kappa(0)=0) のとき：\psi_0(x_0|x_1) = \exp_{x_0}(\mathbf{0}) = x_0
  • t=1 (\kappa(1)=1) のとき：\psi_1(x_0|x_1) = \exp_{x_0}(\log_{x_0}(x_1)) = x_1

これは、ユークリッド空間での線形補間 (1-\kappa(t))x_0 + \kappa(t)x_1 (これは x_0 + \kappa(t)(x_1-x_0) とも書ける) の自然な一般化になっています。実際、ユークリッド空間では \exp_{x_0}(v) = x_0+v, \log_{x_0}(x_1) = x_1-x_0 です。

この測地線フローは、単純な多様体（球面、双曲空間など）で指数・対数写像が閉じた形で計算できる場合には、シミュレーションフリーなフローマッチングを可能にします。これは、多様体上の拡散モデルがしばしば複雑なスコア計算やSDEシミュレーションを必要とするのと対照的です。

4.5.2 プレメトリックを用いたフロー

しかし、一般的な多様体では指数・対数写像の計算が困難であったり、測地線が一意に定まらなかったり（カットローカスを越える場合など）、あるいは測地線が望ましい経路ではない場合もあります（例えば、データが特定の制約を満たすように多様体内に埋め込まれているが、測地線はその制約を破ってしまうなど）。

そこで、より柔軟なアプローチとして、測地距離 d_g(x,y) の代わりに、一般的な「距離のような」関数（プレメトリックと呼ばれる） d(x,y): \mathcal{M} \times \mathcal{M} \to \mathbb{R}_{\ge 0} を導入し、条件付きフローがこのプレメトリックに関する距離を保存するように設計する方法が提案されています（Chen and Lipman, 2024。原著 §5.6）。
具体的には、条件付きフロー \psi_t(x_0|x_1) が以下を満たすようにします（原著 Eq. 5.18）。

d(\psi_t(x_0|x_1), x_1) = \tilde{\kappa}(t) d(x_0, x_1) \tag{\text{原著 Eq. 5.18}}

ここで \tilde{\kappa}(t) は \tilde{\kappa}(0)=1, \tilde{\kappa}(1)=0 を満たす単調減少関数です（例えば \tilde{\kappa}(t) = 1-\kappa(t)）。
この条件を満たすフローに対する最小ノルムの条件付き速度場は、以下のように与えられます（原著 Eq. 5.19）。

u_t(x|x_1) = \frac{d \log \tilde{\kappa}(t)}{dt} d(x,x_1) \frac{\nabla_x d(x,x_1)}{\|\nabla_x d(x,x_1)\|_g^2} \tag{\text{原著 Eq. 5.19}}

（ただし、\nabla_x d(x,x_1) \neq 0 の場合）。
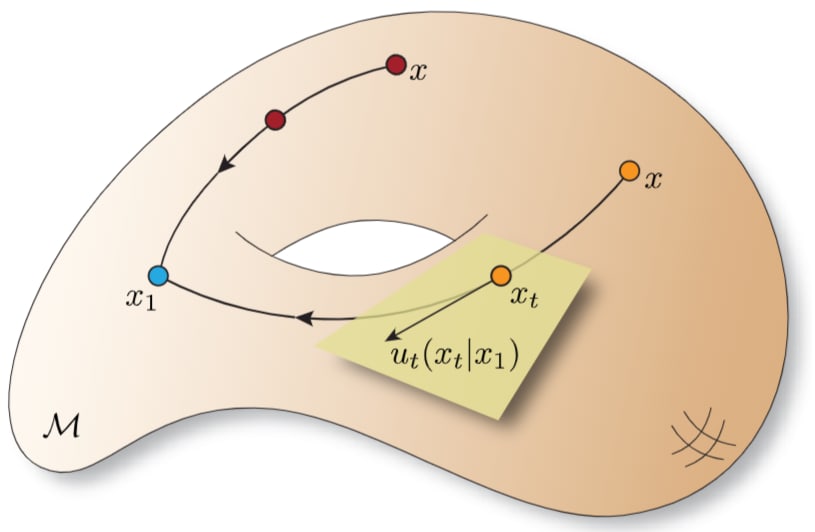
このアプローチの利点は、d(x,y) として測地距離以外のものを選択できることです。例えば、スペクトル距離や、ニューラルネットワークで学習された距離関数などを用いることで、よりデータに適したフローを設計できる可能性があります。ただし、この場合の速度場はプレメトリックの勾配に依存するため、プレメトリックの設計が重要になります。また、一般にはこのフローの経路を陽に計算することはできず、速度場を用いたODEシミュレーションが必要になる場合があります。


図4.2：多様体 \mathcal{M} 上の条件付きフロー。点 x における条件付き速度場 u_t(x|x_1) は、x をターゲット x_1 へと導く。(Meta AI "Flow Matching Guide and Code" Fig. 12 より引用)

4.5.3 測地線フローの課題と対処

測地線フローやプレメトリックフローには、特異点の問題が伴うことがあります。
例えば、球面上での測地線距離 d_g(x,x_1) は、x が x_1 の対蹠点 -x_1 にあるとき微分不可能です。また、一般的な滑らかな関数 x \mapsto d(x,x_1) であっても、その勾配 \nabla_x d(x,x_1) がゼロになる臨界点（最大点や最小点など）が存在し、そこでは上記の速度場が定義できません。

これらの問題に対処するため、実際には以下のような工夫が考えられます。

  • スケジューリング関数の調整: \kappa(t) (または \tilde{\kappa}(t)) を、t だけでなく x_0, x_1 にも依存させることで、特異点を回避するように滑らかにフローを調整する（原著 p.39冒頭）。
  • 非縮退条件の緩和: プレメトリックの勾配がゼロになる点の集合の測度がゼロであれば、実用上は問題ないことが多い（原著 p.39 "Non-degenerate (relaxed)"）。

原著のCode 8では、球面上での測地線フローを用いたフローマッチングの訓練例が示されています。そこでは、モデルが出力した速度ベクトルを、現在の点における接空間に射影する操作が含まれており、これは多様体上で速度場を扱う際の重要な実践的ステップです。

4.6 この章のまとめ：フローマッチングの幾何学的な拡張

この章では、フローマッチングの枠組みをユークリッド空間からリーマン多様体へと拡張する方法を学びました。

  • リーマン多様体は、局所的にユークリッド的だが大域的に曲がった空間であり、リーマン計量によって幾何学的な構造が定義される。
  • 多様体上でも、確率分布、フロー、速度場、連続の方程式、瞬間的変数変換といった概念が自然に定義され、フローマッチングの理論的基礎が保たれる。
  • 周辺化トリックも多様体上で成り立ち、条件付き量をターゲットとした学習（RCFM損失）が正当化される。
  • 多様体上の条件付きフローを構築する主要な方法として、
    • 測地線フロー: 多様体上の「直線」である測地線に沿って点を移動させる。指数・対数写像が計算可能ならシミュレーションフリー学習も可能。
    • プレメトリックフロー: 一般的な距離関数 d(x,y) を用い、フローがこの距離を保存するように速度場を設計する。より柔軟だが、速度場の計算やODEシミュレーションが必要になる場合がある。
  • 特異点の存在など、多様体特有の課題もあるが、実用的な対処法も研究されている。

この拡張により、フローマッチングは、より広範な種類のデータ（特に複雑な幾何学的構造を持つもの）に対して適用可能な、強力で柔軟な生成モデリングのツールとなります。タンパク質構造生成、分子動力学シミュレーション、ロボティクス、コンピュータグラフィックスなど、多様な分野での応用が期待されます。

次章では、フローマッチングのもう一つの重要な拡張として、連続的な空間ではなく、カテゴリカルな値を取るような離散的な状態空間でのフローマッチング（Discrete Flow Matching）について見ていきます。これはテキスト生成などの分野で特に重要となります。

ここまでの議論のポイント：

  • リーマン多様体は曲がった空間。接空間とリーマン計量が重要。
  • フロー、速度場、連続の方程式、周辺化トリックは多様体上にも拡張可能。
  • RCFM損失で学習。
  • 条件付きフローの設計：測地線フロー（指数・対数写像）、プレメトリックフロー。
  • 多様体特有の課題（特異点など）への対処も必要。

第5章 フローマッチングの拡張(2)：離散空間への挑戦

この章のゴール：
これまでの章では、フローマッチングを連続的な空間（ユークリッド空間やリーマン多様体）で扱ってきました。しかし、現実世界の多くのデータ、特に自然言語（テキスト）やカテゴリカルな特徴量は、離散的な状態空間に存在します。この章では、フローマッチングのアイデアを、このような離散的な空間へと拡張する「離散フローマッチング（Discrete Flow Matching, DFM）」について探求します。連続時間マルコフ連鎖（Continuous Time Markov Chain, CTMC）という数学的ツールを導入し、それが離散空間における「フロー」の役割をどのように果たすのかを理解します。そして、DFMがどのようにして確率パスを設計し、生成的な「速度」（遷移率）を学習し、最終的に新しい離散データを生成するのか、そのメカニズムを明らかにします。この章を通じて、フローマッチングの適用範囲が連続空間だけでなく離散空間にも広がり、テキスト生成などの重要なタスクに取り組むための道が開かれることを見ていきます。

（原著の §6 "Continuous Time Markov Chain Models" および §7 "Discrete Flow Matching" の内容に相当する内容です。）

5.1 離散状態空間と連続時間マルコフ連鎖（CTMC）

まず、DFMの舞台となる離散状態空間と、その上でのダイナミクスを記述するCTMCについて理解しましょう。

5.1.1 離散状態空間 (原著 §6.1)

状態空間 \mathcal{S} が有限個のカテゴリからなる集合である場合を考えます。例えば、自然言語処理では、\mathcal{S} は語彙集合（ボキャブラリ） \mathcal{V} の中の単語（トークン）に対応します。データ x は、これらのトークンのシーケンス x = (x^1, x^2, \dots, x^L) であり、各 x^i \in \mathcal{V} です。
簡単のため、まずは1つのトークン（つまり状態空間が \mathcal{S}=\mathcal{V} であり、その要素数を K=|\mathcal{V}| とする）を考えることから始め、後にシーケンスへと拡張します。

離散空間上の確率分布は、確率質量関数（Probability Mass Function, PMF） p(x) で与えられ、x \in \mathcal{S} に対して p(x) \ge 0 かつ \sum_{x \in \mathcal{S}} p(x) = 1 を満たします。
また、ある特定状態 z \in \mathcal{S} のみを確率1で取るデルタ分布を \delta(x,z) （x=z で1、他で0）と書きます。

5.1.2 連続時間マルコフ連鎖 (CTMC) モデル (原著 §6.2)

CTMCは、離散的な状態空間 \mathcal{S} 上を時間的に連続に遷移していく確率過程 (X_t)_{t \ge 0} です。その動きは、以下の2つの要素で特徴づけられます。

  1. 遷移率（Transition Rates）: 状態 x \in \mathcal{S} から状態 y \in \mathcal{S} (y \neq x) へと単位時間あたりに遷移する「速度」または「強度」を表す u_t(y,x) \ge 0。（これは後に学習対象となります。）
  2. 保持時間（Holding Times）: ある状態 x に滞在する時間は、その状態からの総脱出率 \sum_{y \neq x} u_t(y,x) に依存する指数分布に従います。

微小時間 h の間に状態 x から状態 y へ遷移する確率 P(X_{t+h}=y | X_t=x) は、以下のように近似できます（原著 Eq. 6.3）。

P(X_{t+h}=y | X_t=x) \approx \begin{cases} u_t(y,x) h & \text{if } y \neq x \\ 1 - \sum_{z \neq x} u_t(z,x) h & \text{if } y = x \end{cases}

これは、フローモデルにおけるODE \frac{dX_t}{dt} = u_t(X_t) の離散空間・確率過程版と見なすことができます。ここで u_t(y,x) は、状態 x から状態 y への「速度」のような役割を果たします。
u_t(y,x) はレート行列（Rate Matrix）または生成行列（Generator Matrix）とも呼ばれる行列 Q_t の (y,x) 成分 Q_t[y,x] であり、以下の条件を満たします（原著 Eq. 6.4）。

  • u_t(y,x) \ge 0 for y \neq x （非対角成分は非負）
  • \sum_{y \in \mathcal{S}} u_t(y,x) = 0 for all x （各列の和は0、つまり u_t(x,x) = -\sum_{y \neq x} u_t(y,x)）


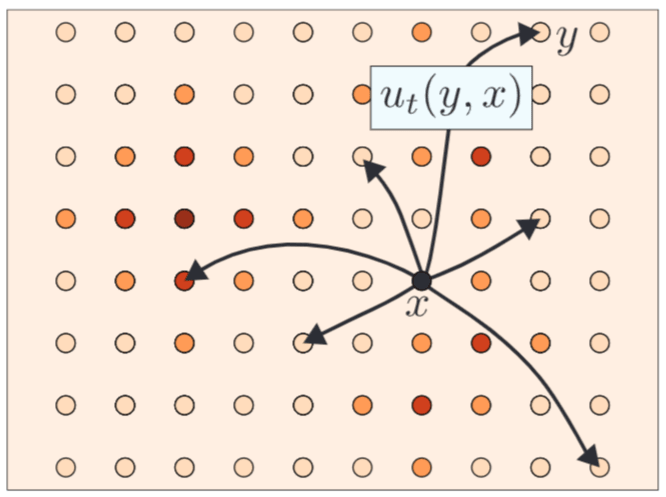
図5.1：CTMCモデル。状態間の確率的な遷移が遷移率（速度） u_t(y,x) によって規定される。(Meta AI "Flow Matching Guide and Code" Fig. 13 より引用)

5.1.3 確率パスとコルモゴロフ方程式 (原著 §6.3)

CTMC (X_t) が時刻 t において状態 x を取る確率（PMF）を p_t(x) と書きます。この p_t(x) の時間発展は、コルモゴロフ方程式（Kolmogorov Equation）によって記述されます（原著 Eq. 6.8）。

\frac{dp_t(y)}{dt} = \sum_{x \in \mathcal{S}} u_t(y,x) p_t(x)

または、ベクトル形式で \frac{dp_t}{dt} = Q_t p_t とも書けます（p_t は p_t(x) を要素とする列ベクトル）。
これは、連続空間での連続の方程式 (2.4) に対応するものです。
ある遷移率 u_t(y,x) が確率パス p_t(x) を生成するとは、このコルモゴロフ方程式が満たされることを意味します。

定理（離散質量保存則、原著 Theorem 13）:
遷移率 u_t(y,x) がレート行列の条件を満たし、p_t(x) がPMFであるとき、コルモゴロフ方程式を満たすことと、u_t(y,x) が p_t(x) を生成することは同値です。

5.2 離散フローマッチング（DFM）の枠組み (原著 §7)

連続空間でのフローマッチングのアイデアを、このCTMCの枠組みを用いて離散空間に持ち込みます。
DFMの目標は、ソースPMF p_0 をターゲットPMF p_1=q へと変換するCTMCを学習することです。これは、そのCTMCを駆動する時間依存の遷移率 u_t^\theta(y,x) をニューラルネットワークでパラメータ化し、学習することを意味します。

DFMのレシピも、連続FMと同様のステップを踏みます。

5.2.1 データと離散確率パスの構築 (原著 §7.1, 7.2)

  1. データ結合: ソースサンプル X_0 \sim p_0 とターゲットサンプル X_1 \sim p_1 の間のカップリング \pi_{0,1}(X_0,X_1) を定義します。
    • テキスト生成のようなタスクでは、p_0 を特別なマスク（MASK）トークンに集中した分布とし、X_1 を実際のテキストトークンとすることがよくあります（独立カップリングの一種）。つまり、\pi_{0,1}(X_0,X_1) = \delta(X_0, \text{MASK}) p_1(X_1)。
  2. 条件付き離散確率パス: 条件変数 Z=z （例えば Z=X_1）が与えられた下での時刻 t のPMF p_{t|z}(x|z) を設計します。
p_t(x) = \sum_{z \in \mathcal{Z}} p_{t|z}(x|z) p_Z(z) \tag{\text{原著 Eq. 7.1}}

境界条件は、 p_{0|z}(x|z) = \pi_{0|z}(x|z) および p_{1|z}(x|z) = \delta_z(x) です。

5.2.2 離散空間の周辺化トリック (原著 §7.3)

連続空間と同様に、離散空間でも周辺化トリックが成り立ちます（原著 Theorem 14）。
もし条件付き遷移率 u_t(y,x|z) が条件付きPMF p_{t|z}(x|z) を（コルモゴロフ方程式の意味で）生成するならば、
周辺遷移率 u_t(y,x) = \mathbb{E}_{Z \sim p_{Z|t}(\cdot|x)} [u_t(y,x|Z)] は周辺PMF p_t(x) を生成します。

5.2.3 離散フローマッチング（DFM）損失 (原著 §7.4)

学習対象の遷移率モデルを u_t^\theta(y,x) とします。
DFM損失は、状態 X_t における遷移率ベクトル u_t(\cdot, X_t) \in \mathbb{R}^{|\mathcal{S}|} （真の遷移率）と u_t^\theta(\cdot, X_t) （モデルの遷移率）の間のBregmanダイバージェンス D_{X_t}(\cdot, \cdot) を用いて定義されます。

\mathcal{L}_{DFM}(\theta) = \mathbb{E}_{t, X_t \sim p_t} [ D_{X_t}(u_t(\cdot, X_t), u_t^\theta(\cdot, X_t)) ] \tag{\text{原著 Eq. 7.4}}

ここで、遷移率ベクトルはレート行列の条件を満たす空間 \Omega_x = \{ v \in \mathbb{R}^{|\mathcal{S}|} | v(y) \ge 0 \forall y \neq x, \sum_y v(y)=0 \} に属します（原著 Eq. 7.5）。

そして、条件付きDFM（CDFM）損失は、

\mathcal{L}_{CDFM}(\theta) = \mathbb{E}_{t, Z \sim p_Z, X_t \sim p_{t|Z}(\cdot|Z)} [ D_{X_t}(u_t(\cdot, X_t|Z), u_t^\theta(\cdot, X_t)) ] \quad (\text{原著 Eq. 7.6})

となります。ここでも、勾配の等価性 \nabla_\theta \mathcal{L}_{DFM}(\theta) = \nabla_\theta \mathcal{L}_{CDFM}(\theta) が成り立ち（原著 Theorem 15）、CDFM損失で学習すれば良いことがわかります。

5.3 因子化パスと速度：シーケンスへの拡張 (原著 §7.5)

ここまでは状態空間 \mathcal{S} が単一のカテゴリカル変数を表す場合を考えてきましたが、テキストのようなシーケンスデータ x = (x^1, x^2, \dots, x^L) （各 x^i \in \mathcal{V}）を扱うには、状態空間の次元が |\mathcal{V}|^L となり、遷移率 u_t(y,x) のサイズが爆発してしまいます。

この問題に対処するため、「因子化速度（factorized velocities）」という考え方を導入します（Campbell et al., 2024; Gat et al., 2024）。
基本的なアイデアは、状態 x から状態 y への遷移が、一度に1つのトークン（座標 i）のみ変化する場合に限定するというものです。
つまり、u_t(y,x) \neq 0 となるのは、y が x の1つの座標 x^i だけを y^i に変えた状態である場合のみとします。
このとき、全体の遷移率 u_t(y,x) は、各座標 i における局所的な遷移率 u_t^i(y^i, x) （状態 x のときに i 番目のトークンが y^i に変わる速さ）の和として書けます（原著 Eq. 7.9）。

u_t(y,x) = \sum_{i=1}^L \delta(y^{\setminus i}, x^{\setminus i}) u_t^i(y^i, x)

ここで x^{\setminus i} は x から i 番目の要素を除いたものです。\delta(y^{\setminus i}, x^{\setminus i}) は、i 番目以外の座標が全て一致していることを要求します。
この u_t^i(y^i, x) は、モデルの出力としては次元 L \times |\mathcal{V}| となり、現実的なサイズになります。


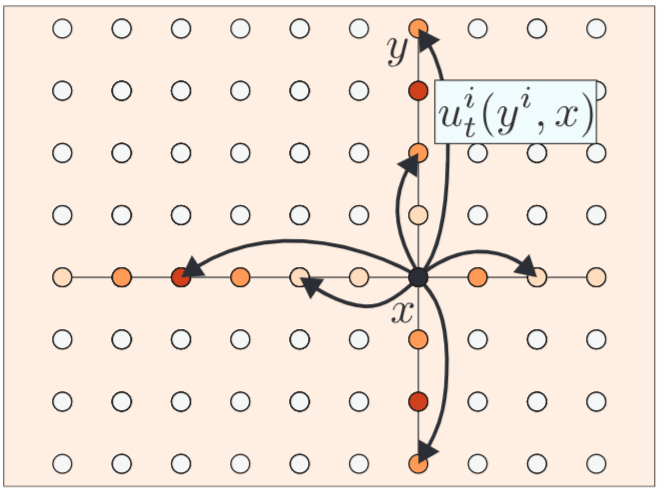
図5.2：因子化CTMCモデル。状態間の非ゼロ遷移率（速度）は、一度に最大1つの座標（トークン）が変化する場合にのみ許される。(Meta AI "Flow Matching Guide and Code" Fig. 14 より引用)

5.3.1 因子化確率パス (原著 §7.5.2)

驚くべきことに、確率パス p_t(x) が各座標ごとに因子化されている場合、つまり、

p_t(x) = \prod_{i=1}^L p_t^i(x^i) \tag{\text{原著 Eq. 7.12}}

（実際にはこれは強すぎる仮定で、原著では条件付きパス p_{t|z}(x|z) = \prod_i p_{t|z}^i(x^i|z) を考えます。原著 Eq. 7.15）、
それを生成する遷移率もまた、上記のような因子化された形になることが示されます（原著 Proposition 2, Theorem 16）。
これにより、学習ターゲットとなる条件付き遷移率も u_t^i(y^i, x|z) という因子化された形で得られ、CDFM損失も各座標ごとに分解して計算できるようになります（原著 Eq. 7.19）。

5.3.2 混合パス (Mixture Paths) とその遷移率 (原著 §7.5.4)

DFMで実用的に用いられる条件付き確率パスの一つが「混合パス（Mixture Path）」です。
条件変数 Z=(X_0, X_1) （ソースとターゲットのペア）が与えられたとき、各座標 i における時刻 t のPMF p_{t|0,1}^i(x^i|X_0,X_1) を、

p_{t|0,1}^i(x^i|X_0,X_1) = \kappa_t \delta(x^i, X_1^i) + (1-\kappa_t) \delta(x^i, X_0^i) \tag{\text{原著 Eq. 7.22}}

と定義します。ここで \kappa_t: [0,1] \to [0,1] は \kappa_0=0, \kappa_1=1 を満たすスケジューリング関数です。
つまり、時刻 t の i 番目のトークン X_t^i は、確率 \kappa_t でターゲットトークン X_1^i となり、確率 1-\kappa_t でソーストークン X_0^i となります。
このパスを生成する因子化された条件付き遷移率 u_t^i(y^i, x^i|X_0,X_1) は、

u_t^i(y^i, x^i|X_0,X_1) = \frac{\dot{\kappa}_t}{1-\kappa_t} [\delta(y^i, X_1^i) - \delta(y^i, x^i)] \quad \text{if } x^i=X_0^i \text{ and } X_0^i \neq X_1^i

（x^i=X_1^i なら遷移しないので0、など場合分けが必要。原著 Eq. 7.24 は x^i が X_0^i か X_1^i かで場合分けして与えています。ここでは x^i=X_0^i から y^i=X_1^i への遷移のみを簡略化して示しました）
という形で与えられます。\dot{\kappa}_t は \kappa_t の時間微分です。
直感的には、まだソース X_0^i のままであるトークンを、ターゲット X_1^i へと変化させる「力」を表しています。

この混合パスと対応する遷移率は、DFMの具体的な実装において非常に重要です。
学習時には、(X_0, X_1) をサンプリングし、時刻 t をランダムに選び、X_t^i を上記の混合ルールで生成し、モデル u_t^{\theta,i}(y^i, X_t) が上記の真の遷移率を予測するように学習します。
サンプリング時には、初期状態（例えば全てMASKトークン）から始め、学習された遷移率 u_t^{\theta,i} を用いてCTMCをシミュレーションし（例えば、各座標で独立にオイラー法などでPMFを更新）、最終的なシーケンスを得ます。

原著のCode 9, 10, 11 は、この混合パスを用いたDFMのPyTorch実装例（おもちゃデータでのスタンドアロンコード含む）を示しており、具体的なアルゴリズムの流れを理解する上で非常に参考になります。

5.4 この章のまとめ：離散データ生成への道筋

この章では、フローマッチングのアイデアを離散状態空間へと拡張するDFMについて学びました。

  • 離散空間でのダイナミクスは、連続時間マルコフ連鎖（CTMC）とその遷移率 u_t(y,x) で記述される。
  • 確率PMFの時間発展はコルモゴロフ方程式に従う。
  • DFMも、(条件付き)離散確率パスの設計と、それを生成する(条件付き)遷移率の回帰学習という2ステップで構成される。
  • 離散空間の周辺化トリックにより、扱いやすい条件付き遷移率をターゲットとしたCDFM損失で学習すれば、目的の周辺遷移率が学習される。
  • シーケンスデータを扱うため、遷移を一度に1トークンに限定する「因子化速度」と、それに対応する「因子化確率パス」を導入する。
  • 実用的なパスとして、ソースとターゲットのトークンを時間に応じて混合する「混合パス」があり、その遷移率は解析的に求められる。

DFMは、フローマッチングの原理をテキストのような重要な離散データに適用するための強力な枠組みを提供します。これにより、従来の自己回帰型モデルとは異なるアプローチで、高品質かつ多様なテキスト生成などが期待されます。

次章では、フローマッチングの考え方をさらに一般化し、フロー（ODE）やCTMCだけでなく、拡散過程（SDE）やジャンプ過程など、より広範なマルコフ過程を統一的に扱える「ジェネレータマッチング（Generator Matching）」という枠組みについて見ていきます。これは、フローマッチングの究極的な形とも言えるでしょう。

ここまでの議論のポイント：

  • 離散空間のダイナミクスはCTMC（遷移率、コルモゴロフ方程式）。
  • DFMは離散確率パスと遷移率学習。周辺化トリックも有効。
  • シーケンスには因子化速度とパスが重要。
  • 混合パスが実用的な選択肢。

第6章 フローマッチングの一般化：ジェネレータマッチング

この章のゴール：
これまでの章で、フローマッチングが連続空間（ユークリッド空間、多様体）や離散空間でどのように機能するかを見てきました。この章では、これらのアイデアをさらに一般化し、フロー（ODE）、連続時間マルコフ連鎖（CTMC）、さらには拡散過程（SDE）やより一般的なジャンプ過程といった、広範な連続時間マルコフ過程（Continuous Time Markov Process, CTMP）を統一的に扱える「ジェネレータマッチング（Generator Matching, GM）」という枠組みを導入します。CTMPの「ジェネレータ（生成作用素）」という数学的対象が、速度場（フロー）や遷移率行列（CTMC）の役割を一般化したものであることを理解し、GMがどのようにしてこのジェネレータを学習し、任意のデータモダリティとマルコフ過程の組み合わせで生成モデルを構築可能にするのか、その強力な統一性と柔軟性を探求します。この章を通じて、フローマッチングが持つポテンシャルの広大さと、生成AIのフロンティアを切り拓くためのより普遍的な原理を掴むことを目指します。

（原著の §8 "Continuous Time Markov Process Models" および §9 "Generator Matching" の内容に相当する内容です。）

6.1 連続時間マルコフ過程（CTMP）とそのジェネレータ

まず、ジェネレータマッチングの基礎となるCTMPとそのジェネレータについて理解を深めましょう。

6.1.1 一般的な状態空間とCTMP (原著 §8.1)

GMは、状態空間 \mathcal{S} が非常に一般的であることを許容します。それは、

  • \mathbb{R}^d （画像、ベクトルなど）
  • 離散集合（言語、カテゴリなど）
  • リーマン多様体（幾何学的データ）
  • あるいはこれらの直積（マルチモーダルデータ、例：画像とテキストのペア）
    であっても構いません。必要なのは、\mathcal{S} がポーランド空間（完備な可分距離空間）であるという、多くの実用的な場合に満たされる技術的な条件のみです。

このような一般の空間 \mathcal{S} 上で定義される確率過程 (X_t)_{t \ge 0} がCTMPであるとは、それがマルコフ性を持つ、つまり、未来の状態の確率は現在の状態のみに依存し、過去の履歴には依存しないことを意味します（原著 Eq. 8.1）。

P(X_{t_{n+1}} \in A | X_{t_1}, \dots, X_{t_n}) = P(X_{t_{n+1}} \in A | X_{t_n})

CTMPは、遷移核（Transition Kernel） P_{s,t}(A|x) = P(X_t \in A | X_s=x) （時刻 s に x にいたとき、時刻 t に集合 A にいる確率）によって完全に特徴づけられます。

6.1.2 ジェネレータ（生成作用素） (原著 §8.2.1)

CTMPの微小時間での振る舞いを記述するのが「ジェネレータ（Infinitesimal Generator）」または「生成作用素」 \mathcal{L}_t です。これは、ある（十分に「良い」）テスト関数 f: \mathcal{S} \to \mathbb{R} に対して作用し、別の関数を返す作用素です。ジェネレータは以下のように定義されます（原著 Eq. 8.8 の形式化）。

[\mathcal{L}_t f](x) = \lim_{h \to 0} \frac{\mathbb{E}[f(X_{t+h}) | X_t=x] - f(x)}{h}

これは、時刻 t に状態 x にいるとき、f(X_t) の期待値の瞬間的な変化率を表します。
このジェネレータ \mathcal{L}_t が、これまで見てきた具体的な過程の「駆動源」を一般化したものになります。

テスト関数 f の役割について

テスト関数 f(x) は、一見すると抽象的で天下り的に感じるかもしれませんが、確率分布や作用素の性質を調べるための数学的に重要な「観測道具」です。

  1. 確率分布の「観測」: 確率分布 p(x) 自体は複雑でも、テスト関数 f を用いた期待値 \mathbb{E}_{X \sim p}[f(X)] はスカラー値となり、分布の特定の側面（平均、分散など）を捉えます。様々な f で期待値を見ることで、p(x) の特徴が明らかになります。数学的には、十分な種類のテスト関数に対する期待値が一致すれば、二つの分布は同一であるとみなせます。

  2. ジェネレータの作用の具体化: ジェネレータ \mathcal{L}_t は確率過程の「変化のルール」ですが、その作用はテスト関数 f を介して [\mathcal{L}_t f](x) という「関数 f の期待される瞬間変化率」として具体化されます。これにより、異なる種類の確率過程（フロー、拡散など）も統一的な枠組みで比較・分析できます。

  3. 数学的一般性と厳密性: テスト関数を用いることで、確率分布が密度関数を持たない場合や、ジェネレータが単純な微分演算子で書けない場合など、より広範な状況を数学的に厳密に扱えるようになります。これは、GMのような一般理論を構築する上で不可欠です。

GMの文脈では、テスト関数は特に後述するコルモゴロフ前向き方程式（KFE）の弱形式での定式化や、ジェネレータをパラメータ化する際のカーネル K_f(x) の定義で中心的な役割を果たします。

  • フロー（ODE）の場合 (原著 §8.2.2, Eq. 8.17):
    d_t X_t = u_t(X_t) dt \implies [\mathcal{L}_t f](x) = \langle \nabla f(x), u_t(x) \rangle
    （速度場 u_t(x) との方向微分）
  • 拡散過程（SDE）の場合 (原著 §8.2.2, Eq. 8.26):
    d_t X_t = \sigma_t(X_t) dW_t \implies [\mathcal{L}_t f](x) = \frac{1}{2} \text{Tr}(\sigma_t(x)\sigma_t(x)^T \nabla^2 f(x))
    （拡散係数 \sigma_t(x) とヘッセ行列 \nabla^2 f(x) を含み、 \frac{1}{2}\sum_{i,j} (\sigma_t\sigma_t^T)_{ij} \frac{\partial^2 f}{\partial x_i \partial x_j} と書き下せる）
  • ジャンプ過程の場合 (原著 §8.2.2, Eq. 8.36):
    遷移強度測度 Q_t(dy, x) を持つ \implies [\mathcal{L}_t f](x) = \int_{\mathcal{S}} [f(y)-f(x)] Q_t(dy,x)
  • CTMC（離散空間のジャンプ過程）の場合 (原著 §8.2.2, Eq. 8.38):
    遷移率行列 u_t を持つ \implies [\mathcal{L}_t f](x) = \sum_{y \in \mathcal{S}} f(y) u_t(y,x) = f^Tu_t
    （最右辺は f をベクトル、 u_t を行列と見た場合の表現）

普遍的表現定理（原著 Theorem 18, §8.4, Eq. 8.68）:
（適切な正則性の下で）ユークリッド空間 \mathbb{R}^d 上の多くのCTMPのジェネレータは、フロー項、拡散項、ジャンプ項の和として表現できることが知られています。

[\mathcal{L}_t f](x) = \underbrace{\langle \nabla f(x), u_t(x) \rangle}_{\text{flow}} + \underbrace{\frac{1}{2} \text{Tr}(\sigma_t(x)\sigma_t(x)^T \nabla^2 f(x))}_{\text{diffusion}} + \underbrace{\int_{\mathcal{S}} [f(y)-f(x)] Q_t(dy,x)}_{\text{jump}}

ここで u_t(x) はドリフト（速度場）、\sigma_t(x)\sigma_t(x)^T は拡散行列、Q_t(dy,x) はジャンプ測度（状態 x から状態 y へのジャンプの強度を表す測度）です。

ジャンプ項（jump term）と補償項について

より一般的なレヴィ過程の理論では、ジャンプ測度 Q_t(dy,x) が非常に小さなジャンプを無限に許容する場合、積分が発散しないように「補償項（compensation term）」がジャンプ項に追加されることがあります。例えば、\int [f(y)-f(x) - \mathbb{I}_{||y-x||<1}\langle \nabla f(x), y-x \rangle] Q_t(dy,x) のような形です。これは、小さなジャンプによるドリフト効果を打ち消すためのものです。

しかし、原著を含め多くのフローマッチングや拡散モデルの文脈では、議論を簡潔にするため、あるいは特定の仮定の下で、上記の補償なしの形式が用いられます。

以下の図6.1（原著の Table 2 より引用）は、フロー、拡散、ジャンプ、CTMCのジェネレータを並べて示しており、この構造を理解する助けになります。


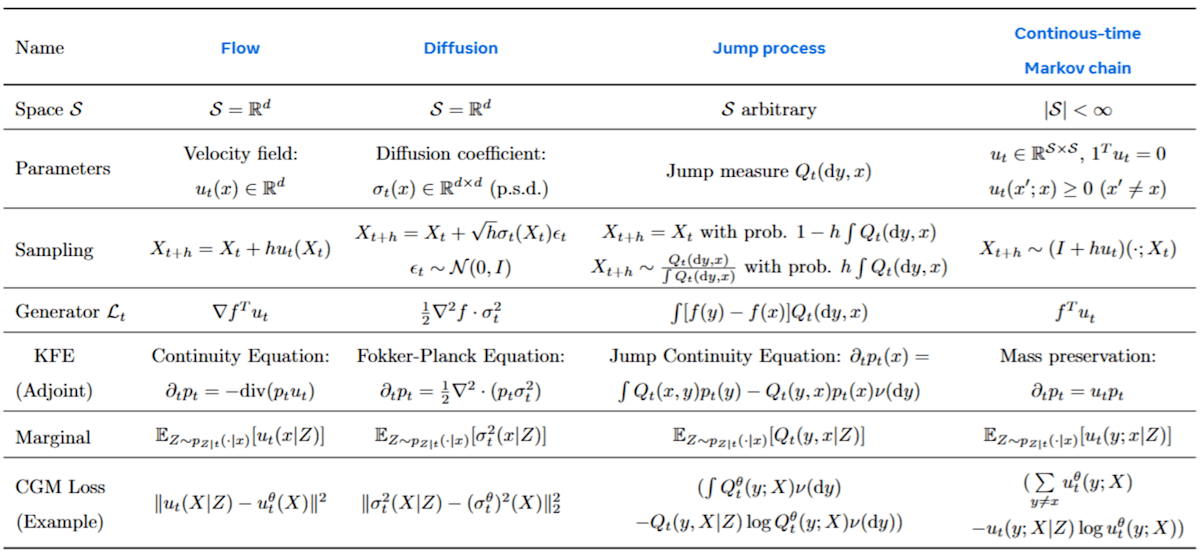
図6.1：CTMP生成モデルの例とジェネレータマッチングによる学習方法。フロー、拡散、ジャンプ過程、連続時間マルコフ連鎖（CTMC）がジェネレータの形で統一的に記述される。(Meta AI "Flow Matching Guide and Code" Table 2 を一部修正 (CTMCのGeneratorの式を修正))

6.1.3 ジェネレータとコルモゴロフ前向き方程式 (原著 §8.3)

マルコフ過程の「瞬間的な変化のルール」であるジェネレータ \mathcal{L}_t が定義されると、次に問題となるのは、このミクロなルールが確率分布 p_t(x) というマクロなシステムの振る舞いを時間とともにどのように変化させるかです。この関係性を記述するのがコルモゴロフ前向き方程式（KFE）です。KFEは、フローマッチングにおける連続の方程式や拡散モデルにおけるフォッカー・プランク方程式といった、具体的な確率分布の時間発展方程式を包括する、より一般的な概念と捉えることができます。

KFEを理解することは、「ジェネレータ \mathcal{L}_t を学習すれば、所望の確率パス p_t を実現できる」というジェネレータマッチングの基本戦略の根幹をなします。なぜなら、KFEこそがジェネレータと確率パスを結びつける方程式だからです。

KFEには主に2つの表現形式があります。

  1. 弱形式（テスト関数とジェネレータを用いた形式）(原著 Eq. 8.40):

    \frac{d}{dt} \langle p_t, f \rangle = \langle p_t, \mathcal{L}_t f \rangle
    • 何をしているか: 左辺は、テスト関数 f で測った「p_t のある側面（期待値）」の時間変化率です。右辺は、ジェネレータ \mathcal{L}_t がテスト関数 f に作用した結果（つまり f の期待される瞬間変化率）を、p_t で平均したものです。
    • 意味: 確率分布 p_t の「ある側面」の変化は、ジェネレータが引き起こす「その側面の期待される変化」を平均したものに等しい、という関係を表します。
    • 利点: p_t が密度関数を持たない場合（例えば、離散分布やデルタ関数を含む分布）でも成り立つ、非常に一般的な形です。

  2. 強形式（密度関数と随伴ジェネレータを用いた形式）(原著 Eq. 8.47):
    もし p_t が（ある参照測度 \nu に関する）密度関数 p_t(x) を持つ場合、KFEは以下のように書けます。

    \frac{d p_t(x)}{dt} = [\mathcal{L}_t^* p_t](x)
    • 何をしているか: 左辺は、各点 x における確率密度 p_t(x) の時間変化率です。右辺は、\mathcal{L}_t^* という別の作用素（\mathcal{L}_t の随伴ジェネレータ(Adjoint Generator)）を現在の密度 p_t に作用させたものです。
    • 意味: 各点での確率密度の時間変化は、現在の確率分布全体に \mathcal{L}_t^* が作用することで決まる、という関係を表します。これは、フローマッチングの連続の方程式や拡散モデルのフォッカー・プランク方程式の一般形です。
随伴ジェネレータ L_t^* の役割について

随伴ジェネレータ \mathcal{L}_t^* は、弱形式のKFEから強形式のKFEを導くための数学的な橋渡しです。
内積 \langle g, h \rangle = \int g(x)h(x)\nu(dx) に関して、\mathcal{L}_t の随伴ジェネレータ \mathcal{L}_t^* は、

\langle g, \mathcal{L}_t f \rangle = \langle \mathcal{L}_t^* g, f \rangle

を満たすものとして定義されます（原著 Eq. 8.41）。これは、作用素 \mathcal{L}_t を内積の「右側」の f から「左側」の g へ移すと、\mathcal{L}_t^* に変わることを意味します。
これを用いると、弱形式のKFEは \left\langle \frac{d p_t}{dt}, f \right\rangle = \langle \mathcal{L}_t^* p_t, f \rangle と変形でき、これが全てのテスト関数 f で成り立つことから強形式のKFEが導かれます。

随伴ジェネレータの具体例:

  • フロー: \mathcal{L}_t f = \langle \nabla f, u_t \rangle \implies \mathcal{L}_t^* p_t = -\nabla \cdot (p_t u_t)
  • 拡散: \mathcal{L}_t f = \frac{1}{2} \text{Tr}(\sigma_t\sigma_t^T \nabla^2 f) \implies \mathcal{L}_t^* p_t = \frac{1}{2} \sum_{i,j} \frac{\partial^2 (\Sigma_{t,ij} p_t)}{\partial x_i \partial x_j} (フォッカー・プランク演算子)

随伴ジェネレータを考えることで、ジェネレータのパラメータ関数（速度場や拡散係数など）が、我々がよく知る密度関数の偏微分方程式の中にどのように現れるかを具体的に見ることができます。

ジェネレータ \mathcal{L}_t が確率パス p_t を生成するとは、これらの（等価な）KFEが成り立つことを意味します。

6.2 ジェネレータマッチング（GM）の枠組み (原著 §9)

GMの目標は、所望の確率パス p_t を生成するようなCTMPのジェネレータ \mathcal{L}_t を学習することです。そのために、ジェネレータをニューラルネットワークでパラメータ化します。

6.2.1 ジェネレータの線形パラメータ化 (原著 §9.3)

多くのCTMPのジェネレータは、テスト関数 f に対して、ある「カーネル」 K_f(x) と、学習対象の「パラメータ関数」 F_t(x) の内積の形で書けることがわかっています。

[\mathcal{L}_t f](x) = \langle K_f(x), F_t(x) \rangle_x \tag{\text{原著 Eq. 9.3}}

ここで \langle \cdot, \cdot \rangle_x は状態 x における適切な内積空間 V_x での内積、F_t(x) はその空間内の元で、かつ実現可能なジェネレータに対応する制約を満たす集合 \Omega_x \subset V_x に属します。
学習するのは、このパラメータ関数 F_t(x) をモデル化したニューラルネットワーク F_t^\theta(x) です。

例：

  • フロー: K_f(x) = \nabla f(x), F_t(x) = u_t(x) (速度場)
  • 拡散: K_f(x) = \frac{1}{2}\nabla^2 f(x), F_t(x) = \sigma_t(x)\sigma_t(x)^T (拡散行列、ただし内積はフロベニウス内積)
  • CTMC: K_f(x) = f (ベクトル), F_t(x) = u_t(\cdot, x) (遷移率ベクトルのx列目)

6.2.2 周辺ジェネレータと条件付きジェネレータ (原著 §9.4)

フローマッチングと同様に、GMでも条件付けと周辺化のトリックを用います。

  1. 条件付き確率パス p_{t|z}(dx|z) を設計する。
  2. それを生成する条件付きジェネレータ \mathcal{L}_t^z （またはそのパラメータ関数 F_t(x|z)）を求める（多くの場合、解析的に可能）。
  3. 周辺化トリックの一般化（原著 Theorem 19）:
    周辺確率パス p_t(dx) = \int p_{t|z}(dx|z) p_Z(dz) は、周辺ジェネレータ \mathcal{L}_t によって生成される。この \mathcal{L}_t のパラメータ関数 F_t(x) は、
F_t(x) = \mathbb{E}_{Z \sim p_{Z|t}(dz|x)} [F_t(x|Z)] \tag{\text{原著 Eq. 9.14}}

と、条件付きパラメータ関数 F_t(x|Z) の事後分布 p_{Z|t}(dz|x) による期待値として与えられる。

6.2.3 ジェネレータマッチング損失 (原著 §9.5)

学習は、ニューラルネットワーク F_t^\theta(x) が真の周辺パラメータ関数 F_t(x) に近づくように、Bregmanダイバージェンスを用いた損失関数を最小化することで行います。

\mathcal{L}_{GM}(\theta) = \mathbb{E}_{t, X_t \sim p_t} [ D_{X_t}(F_t(X_t), F_t^\theta(X_t)) ] \tag{\text{原著 Eq. 9.16}}

そして、フローマッチングと同様に、この損失は勾配が等価な条件付きジェネレータマッチング（CGM）損失に置き換えることができます。

\mathcal{L}_{CGM}(\theta) = \mathbb{E}_{t, Z \sim p_Z, X_t \sim p_{t|Z}(\cdot|Z)} [ D_{X_t}(F_t(X_t|Z), F_t^\theta(X_t)) ] \tag{\text{原著 Eq. 9.17}}

定理（GM損失とCGM損失の勾配の等価性、原著 Theorem 20）:

\nabla_\theta \mathcal{L}_{GM}(\theta) = \nabla_\theta \mathcal{L}_{CGM}(\theta)

かつ、CGM損失の最小解は、所望の周辺パラメータ関数 F_t^\theta(x) = \mathbb{E}_{Z \sim p_{Z|t}(dz|x)} [F_t(x|Z)] を与えます。

この定理がGMの核心であり、これにより、任意のCTMPに対して、扱いやすい条件付きパラメータ関数 F_t(X_t|Z) をターゲットとして回帰学習を行うだけで、目的の複雑な周辺ジェネレータを学習できることが保証されます。

6.2.4 条件付きジェネレータの求め方 (原著 §9.6)

CGM損失で学習するためには、ターゲットとなる条件付きパラメータ関数 F_t(x|z) を知る必要があります。これは、条件付き確率パス p_{t|z}(dx|z) を設計し、それが満たすべきKFE（条件付き版）

\frac{d}{dt} \langle p_{t|z}, f \rangle = \langle p_{t|z}, \mathcal{L}_t^z f \rangle

から、ジェネレータ \mathcal{L}_t^z (ひいては F_t(x|z)) を逆算することで求めます。
原著では、例としてジャンプ過程（混合パスを含む）での F_t(x|z) の導出が示されています。これは、特定のパス設計に対して解析的に解ける場合が多いです。

6.3 モデルの組み合わせと拡張：GMの創造力 (原著 §9.7, 9.8)

ジェネレータマッチング（GM）の強力さは、統一的な学習フレームワークを提供するだけに留まりません。その数学的な構造は、既存のモデルを自在に組み合わせたり、新しい機能を付け加えたりするための、非常に柔軟な「創造のプラットフォーム」として機能します。このセクションでは、その具体的な方法を探ります。

6.3.1 ジェネレータの線形結合：モデルの重ね合わせ (原著 Proposition 3)

この創造力の源泉は、ジェネレータ \mathcal{L}_t と確率パス p_t を結ぶKFEが線形方程式である、という単純かつ強力な事実にあります。これは、線形代数で「方程式 Ax=b の解 x_1, x_2 があれば、その重ね合わせも何らかの関連方程式の解になる」という性質に似ています。原著では、この性質がProposition 3としてまとめられ、モデルを組み合わせるための3つの基本的なレシピを提供します。

Proposition 3（モデルの組み合わせ）:
ある確率パス p_t が与えられたとき、それを生成するジェネレータを構築するための以下の3つの方法が存在します。

  1. マルコフ・スーパーポジション (Markov Superposition):
    もし \mathcal{L}_t と \mathcal{L}_t^{\prime} がそれぞれ同じ確率パス p_t を生成する2つの異なるジェネレータ（例: フローとジャンプ）であるなら、それらの凸結合

    \alpha_t^{(1)} \mathcal{L}_t + \alpha_t^{(2)} \mathcal{L}_t^{\prime}

    （ただし \alpha_t^{(1)}, \alpha_t^{(2)} \ge 0 かつ \alpha_t^{(1)} + \alpha_t^{(2)} = 1）もまた、同じ確率パス p_t を生成する有効なジェネレータとなります。

    • 意味: これは、異なる種類のダイナミクスを「混ぜ合わせる」ことを可能にします。例えば、普段は滑らかに動くフロー（ODE）に、時々ランダムなジャンプを加えるような、よりリッチな挙動を持つモデル（区分的決定的マルコフ過程）を簡単に設計できます。学習は、それぞれのコンポーネントを個別にGMで学習するか、あるいは両方を同時に学習することで行えます。

  2. 発散ゼロ成分の追加 (Divergence-free Components):
    もし \mathcal{L}_t が確率パス p_t を生成するジェネレータであるなら、それに任意の「発散ゼロ（Divergence-free）」なジェネレータ \mathcal{L}_t^{\text{div}} を加えた

    \mathcal{L}_t + \beta_t \mathcal{L}_t^{\text{div}}

    （ただし \beta_t \ge 0）もまた、同じ確率パス p_t を生成します。

    発散ゼロとは？

    ジェネレータ \mathcal{L}_t^{\text{div}} が発散ゼロであるとは、それが確率分布 p_t を変化させない、つまり、\mathcal{L}_t^{\text{div}} だけで駆動される過程は、p_t を定常分布として保つことを意味します。
    数学的には、KFEの右辺がゼロになる、すなわち \langle p_t, \mathcal{L}_t^{\text{div}} f \rangle = 0 が全てのテスト関数 f で成り立つことです。

    • 意味: これは極めて強力な概念です。我々は、元の生成過程の軌道（確率パス p_t）を一切乱すことなく、サンプリングの質を向上させるための「補助的な動き」を自由に追加できるのです。これは、料理のレシピ（確率パス）を変えずに、調理プロセス（サンプリング過程）だけを改善するようなものです。この「補助的な動き」の代表例が、まさにMCMCアルゴリズムです。

  3. 予測子・修正子スキーム (Predictor-Corrector):
    もし \mathcal{L}_t が確率パス p_t を順方向に生成するジェネレータであり、\bar{\mathcal{L}}_t が同じ確率パス p_t を逆方向に生成するジェネレータであるならば、

    \alpha_t^{(1)} \mathcal{L}_t + \alpha_t^{(2)} \bar{\mathcal{L}}_t

    （ただし \alpha_t^{(1)}, \alpha_t^{(2)} \ge 0 かつ \alpha_t^{(1)} - \alpha_t^{(2)} = 1）もまた、同じ確率パス p_t を順方向に生成します。

    なぜこの条件なのか？

    逆時間ジェネレータ \bar{\mathcal{L}}_t は、順時間とは逆向きに分布を変化させる。つまり、KFEの左辺の符号が反転した方程式 \frac{d}{dt} \langle p_t, f \rangle = - \langle p_t, \bar{\mathcal{L}}_t f \rangle を満たす。
    この性質を使うと、新しいジェネレータ \mathcal{L}_t^{\text{PC}} が満たすKFEは、

    \begin{aligned} \langle p_t, \mathcal{L}_t^{\text{PC}} f \rangle &= \langle p_t, (\alpha_t^{(1)} \mathcal{L}_t + \alpha_t^{(2)} \bar{\mathcal{L}}_t) f \rangle \\ &= \alpha_t^{(1)} \langle p_t, \mathcal{L}_t f \rangle + \alpha_t^{(2)} \langle p_t, \bar{\mathcal{L}}_t f \rangle \\ &= \alpha_t^{(1)} \left( \frac{d}{dt} \langle p_t, f \rangle \right) + \alpha_t^{(2)} \left( - \frac{d}{dt} \langle p_t, f \rangle \right) \\ &= (\alpha_t^{(1)} - \alpha_t^{(2)}) \frac{d}{dt} \langle p_t, f \rangle \\ &= \frac{d}{dt} \langle p_t, f \rangle \end{aligned}

    となり、確かに元の順時間KFEを満たすことがわかる。

    • 意味: このスキームは、確率的微分方程式（SDE）に基づく拡散モデルのサンプラーで中心的な役割を果たします。

      • 予測子 (Predictor): \alpha_t^{(1)} \mathcal{L}_t の項は、主に逆時間SDEのドリフト項に対応し、分布を目標（データ分布）に向かって「予測」的に動かす役割を持ちます。
      • 修正子 (Corrector): \alpha_t^{(2)} \bar{\mathcal{L}}_t の項は、逆時間SDEの拡散項（ノイズ）に対応し、サンプリング過程で生じた誤差を「修正」する効果がある。これは、2番の「発散ゼロ成分」の一種と見なすこともでき、各時刻でサンプルを現在の周辺分布 p_t に近づけるように働きます。

      この組み合わせにより、純粋なODE/SDEサンプラー（\alpha_t^{(2)}=0 の場合）よりも安定し、高品質なサンプリングが可能になります。

6.3.2 応用例：MCMCによるサンプリングの改善

Proposition 3の2番目のレシピ「発散ゼロ成分の追加」が、実際にどのように機能するのか、2つの有名なMCMCアルゴリズムを例に見てみましょう。これらのアルゴリズムは、与えられた分布 p_t(x) を不変に保つ（つまり発散ゼロの）ジェネレータを構築する方法を提供します。

  • 例1: ランジュバン動力学 (Langevin Dynamics) (原著 §9.7, Eq. 9.38)
    状態空間が \mathbb{R}^d の場合を考えます。ある分布 p_t(x) が与えられたとき、以下のSDEで記述される過程をランジュバン動力学と呼びます。

    dX_t = \frac{\beta_t^2}{2} \nabla \log p_t(X_t) dt + \beta_t dW_t
    • 何をしているか: この過程は、確率密度の高い方向へ向かうドリフト項（\nabla \log p_t(x)）と、ランダムなノイズ項（dW_t）から成ります。これは、山を登りながらも時々ランダムに揺さぶられる登山者のような動きです。
    • なぜ発散ゼロなのか: このSDEに対応するジェネレータの随伴作用素（フォッカー・プランク演算子）を p_t に作用させると、ドリフト項からの寄与と拡散項からの寄与が完璧に打ち消し合い、結果として [\mathcal{L}_t^{\text{Langevin}}]^* p_t = 0 となります。これは、この過程が p_t を時間変化させない、つまり発散ゼロであることを意味します。
    • GMでの活用: この事実により、我々は任意のGMモデル（フロー、ジャンプなど）のジェネレータ \mathcal{L}_t に、このランジュバン動力学のジェネレータ \mathcal{L}_t^{\text{Langevin}} を自由に追加できます。これにより、生成過程の途中で各時刻の分布 p_t に沿ってサンプルを「リフレッシュ」させ、より高品質なサンプルを得ることが期待できます。これは、拡散モデルにおける確率的サンプラー（SDE-based sampler）の理論的基盤となります。

  • 例2: メトロポリス・ヘイスティングス (Metropolis-Hastings)
    より一般的な状態空間（離散空間を含む）では、メトロポリス・ヘイスティングスアルゴリズムが発散ゼロのジャンプ過程を構築する方法を提供します。これは、提案分布からのジャンプを、詳細釣り合い条件を満たすような採択確率で受け入れる/棄却する手続きです。

    Q_t(y,x)p_t(x) = Q_t(x,y)p_t(y)

    この条件を満たすジャンプ過程のジェネレータは、自動的に発散ゼロになります。したがって、どんなGMモデルにも、この種のメトロポリス的なジャンプを追加して、サンプリングを改善することが可能です。

6.3.3 マルチモーダルモデルへの道

GMの一般性は、状態空間が複数のモダリティの直積 \mathcal{S} = \mathcal{S}_1 \times \mathcal{S}_2 （例: 画像×テキスト）であっても揺るぎません。これは、GMが状態空間の具体的な構造に依存しない、極めて抽象的なレベルで構築されているためです。これにより、マルチモーダルデータの生成を、単一モーダルの場合と全く同じ原理で扱えます。さらに、確率パスを賢く設計（例: 因子化）することで、それぞれのモダリティ用に事前学習された既存のモデルを「部品」として再利用し、効率的に組み合わせることも可能になり、スケーラブルなマルチモーダル生成モデルの構築への道を開きます。

6.4 この章のまとめ：フローマッチングの究極形へ

この章では、フローマッチングの考え方を極限まで一般化したジェネレータマッチング（GM）について学びました。

  • GMは、任意のデータモダリティ（状態空間 \mathcal{S}）と任意の連続時間マルコフ過程（CTMP）を扱える統一的な生成モデリングのフレームワークである。
  • CTMPのダイナミクスは、その「ジェネレータ（生成作用素）」 \mathcal{L}_t によって微視的に特徴づけられる。ジェネレータは、フローの速度場やCTMCの遷移率行列などを一般化した概念である。
  • 確率パス p_t とジェネレータ \mathcal{L}_t は、コルモゴロフ前向き方程式（KFE）で結ばれる。
  • GMの学習は、ジェネレータの「パラメータ関数」 F_t(x) をニューラルネットワークでモデル化し、条件付きパラメータ関数 F_t(x|Z) をターゲットとするCGM損失を最小化することで行われる。一般化された周辺化トリックにより、この学習が正当化される。
  • GMは、異なる種類のモデルの組み合わせや、マルチモーダルデータの生成も自然にサポートする。

GMは、フローマッチングが持つ柔軟性と強力さを最大限に引き出し、まさに「任意のデータ」を「任意の過程」で生成するための普遍的な設計図を提供します。これにより、これまで個別に研究されてきた多くの生成モデル（フロー、拡散、自己回帰など）を統一的な視点から理解し、それらを自在に組み合わせて新しいモデルを創造する道が開かれます。

次章では、このGMの視点から、特に重要なクラスのモデルである拡散モデル（および関連するノイズ除去モデル）がどのように位置づけられるのかを再訪し、フローマッチングと拡散モデルの関係性をより深く掘り下げます。

ここまでの議論のポイント：

  • GMは任意のデータ・マルコフ過程を扱える究極のFM。
  • CTMPはジェネレータ \mathcal{L}_t で特徴づけられる。\mathcal{L}_t が速度場や遷移率の一般化。
  • p_t と \mathcal{L}_t はKFEで結ばれる。
  • GM学習は、ジェネレータのパラメータ関数 F_t(x) をCGM損失で学習。
  • モデルの組み合わせやマルチモーダル生成も可能。

第7章 フローマッチッチングと拡散モデル：共通点と相違点

この章のゴール：
フローマッチング（FM）と拡散モデル（Denoising Diffusion Models, DDM）は、現代の生成モデリングを牽引する二大パラダイムです。一見すると、それぞれ異なる理論的背景から発展してきたように見えますが、実は両者の間には深く、そして本質的な繋がりが存在します。この最終章では、これまで学んできたフローマッチング、そしてその一般化であるジェネレータマッチング（GM）の視点から、拡散モデルを再訪します。拡散モデルがどのようにFM/GMの特殊なケースとして位置づけられるのかを、時間パラメータの慣習、確率パスの構築、学習アルゴリズム、サンプリング手法、そして時間反転の役割という5つの重要な側面から徹底的に比較・分析します。この章を通じて、二つのアプローチが共通の数学的原理を共有していることを理解し、同時にフローマッチングがなぜより高い柔軟性と一般性を提供するのか、その理由を明らかにします。これは、個別のモデルを越えた、生成モデリングのより普遍的な原理を掴むための重要なステップとなるでしょう。

（原著の §10 "Relation to Diffusion and other Denoising Models" に相当する内容です。）

7.1 時間パラメータの慣習の違い (原著 §10.1)

フローマッチングと拡散モデルを比較する上で、最初に解消しておくべき混乱の元は、時間のパラメータ化に関する慣習の違いです。これは単なる表記上の問題ですが、両者の理論を結びつける上で非常に重要です。

  • フローマッチング（FM）の時間 t:
    本記事で一貫して用いてきたように、FMでは時間は t=0 から t=1 へと進みます。

    • t=0: ノイズ（ソース分布 p_0）
    • t=1: データ（ターゲット分布 p_1=q）

  • 拡散モデル（DDM）の時間 r:
    一方、多くの拡散モデルの論文では、時間は逆向きにパラメータ化されます。フォワードプロセス（ノイズ付加）は r=0 から始まり、時間が進むにつれてノイズが増えていきます。サンプリング（ノイズ除去）は、大きな時間（例えば r=T や r=+\infty）から r=0 へと時間を遡って行われます。混乱を避けるため、ここでは拡散モデルの時間を r とし、以下のように定義します。

    • r=0: データ（分布 q）
    • r=+\infty: ノイズ（ガウス分布など）

この2つの時間軸を対応させるために、単調減少する連続関数 k を用いて時間の再パラメータ化を行います。

\begin{align} \text{FM時間 } t: \quad &t=0 \text{ (ノイズ)} \to t=1 \text{ (データ)} \tag{原著 Eq. 10.1} \\ \text{拡散時間 } r: \quad &r=0 \text{ (データ)} \to r=+\infty \text{ (ノイズ)} \tag{原著 Eq. 10.2} \\ \text{相互変換}: \quad &r = k(t), \quad t = k^{-1}(r) \tag{原著 Eq. 10.3} \end{align}

ここで、相互変換に用いる関数 k: (0, 1] \to [0, +\infty) は、以下の性質を持つものとします。

  • k(1) = 0 （FMのデータ時点 t=1 は、拡散のデータ時点 r=0 に対応）
  • \lim_{t \to 0} k(t) = +\infty （FMのノイズ時点 t=0 は、拡散のノイズ時点 r=+\infty に対応）

この対応関係を念頭に置くことで、拡散モデルのフォワードプロセスや学習則を、フローマッチングの確率パスや損失関数として解釈することが可能になります。

7.2 フォワードプロセスと確率パス (原著 §10.2)

拡散モデルの根幹をなすのは、データ分布 q を徐々にノイズへと変換していく「フォワードプロセス（Forward Process）」です。このプロセスは、通常、以下の確率微分方程式（SDE）によって定義されます。

d X_r = a_r(X_r) dr + g_r dW_r, \quad X_0 \sim q \tag{原著 Eq. 10.4}

ここで、

  • X_r は拡散時間 r における状態（データ）。
  • a_r(x) はドリフト項（速度場に相当）。
  • g_r は拡散係数（ノイズの強さ）。
  • W_r は標準的なウィーナー過程（ブラウン運動）。
  • 初期条件 X_0 はデータ分布 q からサンプリングされます。

このSDEは、時間とともにデータにノイズを付加していく過程を記述します。
さて、このフォワードプロセスは、フローマッチングの観点から見ると何に対応するのでしょうか？
答えは、「特定の確率パスを構築するための一つの具体的な方法」です。

第6章で学んだように、任意の連続時間マルコフ過程（このSDEもその一つ）は、確率パスを定義します。具体的には、

  • 条件付き確率パス \tilde{p}_{r|0}(x|z): 初期状態が X_0=z であったときの、時刻 r における状態 X_r の確率分布 P(X_r=x|X_0=z)。
  • 周辺確率パス \tilde{p}_r(x): 初期状態がデータ分布 X_0 \sim q に従うときの、時刻 r における状態 X_r の確率分布 P(X_r=x)。
チルダ ~ 表記について

以降、混乱を避けるために、

  • 拡散時間 r で定義される確率分布やそのパラメータにはチルダ ~ を付けて表記
    （\tilde{p}_r, \tilde{\alpha}_r, \tilde{\sigma}_r）
  • フローマッチング時間 t で定義されるものにはチルダを付けずに表記
    （p_t, \alpha_t, \sigma_t）

することで両者を区別します。

これらをFM時間 t に変換すると、それぞれ p_{t|1}(x|z) = \tilde{p}_{k(t)|0}(x|z) と p_t(x) = \tilde{p}_{k(t)}(x) となり、フローマッチングで用いる確率パスそのものが得られます。

7.2.1 アフィン・ドリフトとガウスパス

拡散モデルの理論と実践において特に重要なのは、フォワードSDEが解析的に解ける場合です。これは主に、ドリフト項 a_r(x) がアフィン形式、すなわち a_r(x) = \alpha_r x （\alpha_r は時間 r に依存するスカラー関数）を持つ場合に実現されます。
このとき、SDEの解である条件付き確率パス \tilde{p}_{r|0}(x|z) は、ガウス分布になることが知られています（原著 Eq. 10.7）。

\tilde{p}_{r|0}(x|z) = \mathcal{N}(x | \tilde{\alpha}_r z, \tilde{\sigma}_r^2 I) \tag{原著 Eq. 10.7}

ここで、\tilde{\alpha}_r = \exp(\int_0^r \alpha_w dw) と \tilde{\sigma}_r^2 は、それぞれドリフトと拡散の効果を時間積分したものです。
この式をFM時間 t で書き直すと、

p_{t|1}(x|z) = \tilde{p}_{k(t)|0}(x|z) = \mathcal{N}(x | \alpha_t z, \sigma_t^2 I) \tag{原著 Eq. 10.8}

となります。ただし、\alpha_t := \tilde{\alpha}_{k(t)} および \sigma_t := \tilde{\sigma}_{k(t)} と定義しました。
この式は、我々が第3章の§3.7.1で議論したフローマッチングにおける「ガウス確率パス」と全く同じ形をしています。

つまり、以下の重要な結論が得られます。
拡散モデルで一般的に用いられるフォワードプロセス（アフィン・ドリフトを持つSDE）は、フローマッチングにおけるガウス確率パスを構築する一つの方法に他なりません。

したがって、拡散モデルは、フローマッチングの枠組みの中で、特定の確率パス（ガウスパス）を選択した場合として捉えることができます。

7.3 学習：ノイズ除去スコアマッチングはフローマッチングの一種 (原著 §10.3)

次に、モデルの学習方法を比較します。拡散モデルは、「ノイズ除去スコアマッチング（Denoising Score Matching, DSM）」という損失関数を用いて学習されます。これは、ノイズが加わったデータ X_r から、元のデータ X_0 を復元する方向の「スコア」（対数確率密度の勾配 \nabla_x \log \tilde{p}_{r|0}(x|X_0)）を予測するものです。
一方、フローマッチングは、速度場 u_t^\theta(x) を回帰学習するCFM損失を用います。

驚くべきことに、拡散モデルのDSM損失は、フローマッチングの特定のCFM損失と等価であることが示せます。
原著では、FMの損失として「x_0予測（X_0予測）」を用いる場合を考え、それがDSM損失に帰着する過程を明らかにしています。

まず、x_0予測のCFM損失は、以下のように書けます。
モデル x_{0|t}^\theta(X_t) が、ノイジーなデータ X_t から元のクリーンなデータ X_0 を予測するように学習します。

\mathcal{L}_{CFM, x_0}(\theta) = \mathbb{E}_{t, X_0 \sim q, Z \sim \mathcal{N}(0,I)} \left[ \| x_{0|t}^\theta(\alpha_t X_0 + \sigma_t Z) - X_0 \|^2 \right] \tag{*}

ここで、X_t = \alpha_t X_0 + \sigma_t Z は、ガウスパス (10.8) に従ってサンプリングされたノイジーなデータです。
この損失関数は、以下の2つのステップでDSM損失と等価な形に変形できます。

(i) ネットワークの再パラメータ化:
まず、学習するネットワークを x_0 予測モデル x_{0|t}^\theta から、スコア予測モデル s_t^\theta へと再パラメータ化します。第3章「3.7 アフィン条件付きフローとその仲間たち」（原著 §4.8.2, Table 1）で見たように、x_0予測、速度場予測、スコア予測の間には線形な関係があります。ガウスパスの場合、最適な x_0 予測 \mathbb{E}[X_0|X_t=x] とスコア \nabla \log p_t(x) の関係から、以下の関係式が導かれます。

s_t^\theta(x) = -\frac{x - \alpha_t x_{0|t}^\theta(x)}{\sigma_t^2} \quad \iff \quad x_{0|t}^\theta(x) = \frac{x + \sigma_t^2 s_t^\theta(x)}{\alpha_t}

この関係を用いることで、ネットワークの出力をスコアとして解釈し直すことができます。

(ii) 損失の変形:
次に、最適解の性質を利用します。
x_0予測の最適解は、条件付き期待値 x_{0|t}^{\theta^*}(x) = \mathbb{E}[X_0 | X_t = x] です。
また、ノイズ除去スコアマッチングのターゲットとなるスコアは、条件付き分布のスコア \nabla_x \log p_{t|1}(x|X_0) です。ガウスパス (10.8) の場合、これは簡単に計算できて、

\nabla_x \log p_{t|1}(x|X_0) = -\frac{x - \alpha_t X_0}{\sigma_t^2}

となります。
モデルのスコア予測 s_t^\theta(X_t) と、この真の条件付きスコアとの二乗誤差を考えると、

\begin{aligned} \left\| s_t^\theta(X_t) - \nabla_x \log p_{t|1}(X_t|X_0) \right\|^2 &= \left\| s_t^\theta(X_t) - \left(-\frac{X_t - \alpha_t X_0}{\sigma_t^2}\right) \right\|^2 \\ &= \left\| -\frac{X_t - \alpha_t x_{0|t}^\theta(X_t)}{\sigma_t^2} + \frac{X_t - \alpha_t X_0}{\sigma_t^2} \right\|^2 \\ &= \left\| \frac{\alpha_t (x_{0|t}^\theta(X_t) - X_0)}{\sigma_t^2} \right\|^2 \\ &= \left( \frac{\alpha_t}{\sigma_t^2} \right)^2 \left\| x_{0|t}^\theta(X_t) - X_0 \right\|^2 \end{aligned}

この関係から、元の x_0 予測損失 (*) を最小化することは、重み付きのDSM損失を最小化することと等価であることがわかります（多くの場合、重みは無視されるか、損失の定義に含められます）。
原著では、この関係性を利用して、\mathcal{L}_{CFM}(\theta) がDSM損失と等価な形式に書き換えられることを示しています（原著の(i)と(ii)の式変形）。

\mathcal{L}_{CFM, x_0}(\theta) \propto \mathbb{E}_{t, X_0 \sim q, X_t \sim p_{t|1}(\cdot|X_0)} \sigma_t^2 \left\| s_t^\theta(X_t) - \nabla_x \log p_{t|1}(X_t|X_0) \right\|^2

結論として、拡散モデルの学習アルゴリズム（ノイズ除去スコアマッチング）は、フローマッチングの枠組みにおいて、以下の特定の条件下での学習と等価です。

  1. 確率パス: ガウス確率パス（アフィン・ドリフトを持つSDEから導かれる）を用いる。
  2. パラメータ化: 速度場をスコア関数で再パラメータ化する（または x_0 予測を用いる）。

これは、フローマッチングがいかに拡散モデルの学習を自然に包含しているかを示す、非常に強力な結果です。

7.4 サンプリング：確率フローODEとSDE (原著 §10.4)

次に、学習済みモデルからのサンプリング方法を比較します。拡散モデルでは、主に2種類のサンプリング手法が用いられます：決定論的なODEサンプリングと確率的なSDEサンプリングです。これらもまた、FM/GMのサンプリング手法の特殊ケースとして理解できます。

7.4.1 決定論的サンプリング（ODE）

拡散モデルからの決定論的サンプリングは、「確率フローODE（Probability Flow ODE）」を解くことで行われます。これは、フォワードSDE (10.4) と同じ周辺分布 \tilde{p}_r(x) を生成する、以下のODEです。

d X_r = \left[ a_r(X_r) - \frac{1}{2}g_r^2 \nabla_x \log \tilde{p}_r(X_r) \right] dr

このODEを、学習されたスコア関数 s_r^\theta(x) \approx \nabla_x \log \tilde{p}_r(x) を用いて、ノイズ（r \approx +\infty）からデータ（r=0）へと逆向きに解きます。
このプロセスをフローマッチングの視点から見てみましょう。
FMでは、学習された周辺速度場 u_t(x) を用いて、ODE \frac{dX_t}{dt} = u_t(X_t) を t=0 から t=1 へと解きます。
これら二つのODEは、時間再パラメータ化 r=k(t) を通じて、実は同じものであることが示せます。
まず、確率フローODEをFM時間 t に変換します。dr = \dot{k}(t)dt （\dot{k}(t)は k(t) の時間微分）なので、

\frac{dX_t}{dt} = \left[ a_{k(t)}(X_t) - \frac{1}{2}g_{k(t)}^2 \nabla_x \log \tilde{p}_{k(t)}(X_t) \right] \dot{k}(t)

となります。右辺が、FMの速度場 u_t(x) に対応します。原著の式 (10.12) は、この関係をアフィン・ドリフト a_r(x)=\alpha_r x と、学習されたスコア関数 s_t^\theta(x) を使って書き下したものです。

u_t(x) = \dot{k}(t) \left[ \alpha_{k(t)} x - \frac{g_{k(t)}^2}{2} s_t^\theta(x) \right] \tag{原著 Eq. 10.12}

この式は、第3章で見た、ガウスパスの場合の周辺速度場とスコア関数の関係式（原著 Eq. 4.78, 10.11）と一致します。
したがって、拡散モデルの確率フローODEによるサンプリングは、フローマッチングにおけるODEサンプリングと完全に等価です。

7.4.2 確率的サンプリング（SDE）

拡散モデルのもう一つのサンプリング方法は、フォワードSDE (原著 Eq. 10.4) を時間反転させた「リバースSDE」を解くことです。このリバースSDEもまた、学習されたスコア関数を用いてシミュレーションされます。
一方、第6章の「6.3.2 応用例：MCMCによるサンプリングの改善」（原著 §9.7）で、任意のCTMP生成モデルに「ランジュバン動力学」を追加できることを見ました。これは、決定論的なフローに確率的なノイズ項を加えることに相当します。
確率フローODEにランジュバン動力学を追加したSDEは、以下のようになります（原著 Eq. 10.15）。

d X_t = \left( u_t(X_t) + \frac{1}{2}\beta_t^2 \nabla_x \log p_t(X_t) \right) dt + \beta_t dW_t

ここで u_t(X_t) は確率フローODEのドリフト項、\beta_t は追加するノイズの強さを制御するパラメータです。
拡散モデルのリバースSDEは、この一般化されたSDEにおいて、特定のノイズ強度 \beta_t を選択した場合として導出できます（具体的には \beta_t = \sqrt{|\dot{k}(t)|} g_{k(t)} となります）。

したがって、拡散モデルのSDEサンプリングは、ジェネレータマッチングの枠組みで、確率フローに特定のランジュバン動力学を追加したサンプリング手法と等価です。
GMの視点からは、追加するノイズの強さ \beta_t は自由に調整できるため、拡散モデルのリバースSDEは、可能なサンプリング手法の広大なファミリーの中の一点に過ぎないことがわかります。

7.5 時間反転の役割：必要か、十分か？ (原著 §10.5)

拡散モデルの理論では、「時間反転（Time Reversal）」の概念が中心的な役割を果たします。サンプリング過程（リバースプロセス）は、ノイズ付加過程（フォワードプロセス）を時間反転させることで数学的に導出されます。
この時間反転の考え方は、フローマッチングやジェネレータマッチングの文脈ではどのように捉えられるのでしょうか？

まず、原著の表記に従い、拡散モデルが学習しようとする「リバースプロセス」を \bar{X}_r と書くことにします。これは、時間 r=0 から r=R へと進む確率過程で、ノイズからデータを生成することを目的とします。一方、フォワードプロセスは X_r で、データからノイズへと向かいます。

拡散モデルにおける「時間反転」には、実は2つの異なるレベルの要求が存在します。

  1. 周辺分布の一致（Marginal Reversal）: リバースプロセス \bar{X}_r が、フォワードプロセス X_r の周辺分布の時間を反転させたものと一致すること。つまり、任意の r \in [0, R] に対して、

    \bar{X}_r \stackrel{d}{=} X_{R-r}

    が成り立つことです。ここで \stackrel{d}{=} は分布が等しいことを意味します。言い換えれば、\bar{X}_r が従う確率分布は、\tilde{p}_{R-r} となります。

  2. 厳密な時間反転（Strict Time Reversal）: 単に各時点での周辺分布が一致するだけでなく、過程全体の同時分布が一致すること。

この2つの概念を念頭に置き、3つの等価な問題設定を比較してみましょう。

  1. 周辺分布の時間反転 (Time-reverse marginals):
    • フォワードプロセス X_r が生成する周辺分布 \tilde{p}_r に対して、\bar{X}_r \sim \tilde{p}_{R-r} となるようなリバースプロセス \bar{X}_r を駆動するODEやSDEを見つける。
    • 拡散モデル（DDM）のアプローチ。
  2. 確率パスの生成 (Generate probability path):
    • ターゲットとなる確率パス p_t （拡散時間では \tilde{p}_{k(t)}）を生成するようなODEやSDEを見つける。
    • フローマッチング（FM）のアプローチ。
  3. KFEを解く (Solve KFE):
    • 確率パス p_t が満たすべきコルモゴロフ前向き方程式（KFE）を解くような過程（ジェネレータ）を見つける。
    • ジェネレータマッチング（GM）のアプローチ。

これら3つの問題は、実質的に同じゴールを目指しています。それは、「所望の周辺分布の系列（＝確率パス）をたどるようなダイナミクスを見つける」ということです。時間反転は、この問題を解くための強力な一つのツールですが、唯一の方法ではありません。

次に、より強い条件である「厳密な時間反転」について考えます。これは、拡散モデルのオリジナルの理論（Anderson, 1982）で議論されている概念で、任意の時間点の集合 \{r_1, \dots, r_n\} と可測集合 \{A_1, \dots, A_n\} に対して、同時分布が一致することを要求します（原著 Eq. 10.18）。

P(\bar{X}_{r_1} \in A_1, \dots, \bar{X}_{r_n} \in A_n) = P(X_{R-r_1} \in A_1, \dots, X_{R-r_n} \in A_n) \quad (\text{原著 Eq. 10.18})

この式が意味するのは、リバースプロセス \bar{X} の任意の軌跡の確率は、フォワードプロセス X の対応する時間を反転させた軌跡の確率と等しいということです。これは非常に強い制約です。

しかし、生成モデリングの多くの応用では、最終的なサンプル X_1（拡散時間では X_0、リバースプロセスでは \bar{X}_R）の分布がデータ分布 q と一致することが目的であり、途中の経路の同時分布までが重要となるケースは稀です。
この観点から見ると、厳密な時間反転は、生成モデリングの目的を達成するためには過剰な制約である可能性があります。

有名な例が、前節で見た確率フローODEです。確率フローODEを解いて得られるリバースプロセスは、一般にフォワードSDEの厳密な時間反転ではありません（つまり、同時分布は一致しない）。しかし、それはフォワードSDEと全く同じ周辺分布を生成し（つまり、周辺分布の一致は満たす）、かつSDEサンプラーよりも少ないステップ数で高品質なサンプルを生成できることが多く、現在の最先端手法となっています。

これは、厳密な時間反転という「より難しい数学的問題」を解くことが、必ずしも実用上最良の結果をもたらすとは限らないことを示唆しています。FM/GMの枠組みは、この「厳密な時間反転」という制約から解放され、同じ確率パスを生成する多様なダイナミクス（ODEやSDEのファミリー）の中から、より効率的なものを選択する自由を提供します。重要なのは、どの方法を選んでも「周辺分布の一致」という生成モデルの基本的な要件は満たされるという点です。

7.6 その他のノイズ除去モデルとの関係 (原著 §10.6)

拡散モデルの成功に触発され、リーマン多様体上のデータや、その他のモダリティ（テキスト、グラフなど）に対しても、「フォワードプロセスでノイズを加え、それを時間反転させて復元する」というアプローチを取る「ノイズ除去モデル（Denoising Models）」が数多く提案されてきました。

これらのモデルとGMの関係は、これまで見てきたDDMとFM/GMの関係と全く同じです。
一般的に、これらのノイズ除去モデルは、特定のGMモデルとして以下のように特徴づけることができます。

  1. 時間パラメータの慣習: DDMと同様に、時間が 0 でデータに対応する「拡散時間」の慣習を用いる。
  2. 確率パスの構築: 「フォワード」または「ノイズ付加」過程を設計することで、暗黙的に確率パスを定義する。
  3. KFEの解法: 対応するKFE（またはその離散版）を解くための一つの特定の方法として、フォワードプロセスの「時間反転」を用いる。

GMのフレームワークは、これらのモデルを個別のトリックの集まりとしてではなく、統一的な原理（確率パスの設計とジェネレータの学習）に基づいた、広大なモデル空間の中の特定の点として理解することを可能にします。これにより、異なるモデル間の比較や、新しいモデルの設計がよりシステマティックに行えるようになります。

7.7 まとめ：統一的な視点からの再訪

この章では、フローマッチング（FM）と拡散モデル（DDM）の関係性を、FMの一般化であるジェネレータマッチング（GM）の視点から深く掘り下げました。両者は別々の道を歩んできたように見えますが、その根底には共通の原理が流れています。

  • 拡散モデルはFM/GMの特殊ケース: DDMで用いられる時間パラメータ、フォワードプロセス（ガウスパス）、学習則（ノイズ除去スコアマッチング）、サンプリング手法（確率フローODE、リバースSDE）はすべて、FM/GMの枠組みにおける特定の選択肢に対応する。
  • FM/GMはより高い柔軟性を提供: FM/GMは、確率パスの設計、学習ターゲット（速度場、スコア、x_0予測など）、サンプリングダイナミクス（ODE/SDEファミリー）の選択において、DDMよりもはるかに大きな自由度を提供する。
  • 時間反転の再評価: DDM理論で中心的な時間反転は、所望の確率パスを生成する過程を見つけるための強力なツールの一つですが、唯一の、あるいは常に最良の方法とは限りません。FM/GMは、この制約から解放された、より広い視野を提供する。

結論として、拡散モデル（DDM）は、ジェネレータマッチング（GM）という広大なフレームワークの中で、特定の（しかし非常に強力で効果的な）設計選択を行った、輝かしい成功例であると位置づけることができます。FM/GMは、DDMの成功の根底にある原理を抽出し、それをより柔軟で拡張性の高い形で提供することで、次世代の生成モデリングの新たな地平を切り拓いています。

ここまでの議論のポイント：

  • FM/GMとDDMは深く関連し、DDMはGMの特殊ケースと見なせる。
  • DDMのフォワードプロセスは、FMのガウスパス設計に対応する。
  • DDMのスコアマッチング学習は、FM/GMの特定の条件下での学習と等価。
  • DDMのサンプリング手法（ODE/SDE）も、FM/GMのサンプリングの特殊ケースとして理解できる。
  • 時間反転はDDMの強力な指針だが、FM/GMの枠組みでは必須ではない。FM/GMはより柔軟な設計を許容する。

おわりに

本記事では、Meta AIの包括的なガイド「Flow Matching Guide and Code」を道しるべとして、フローマッチングという新時代の生成モデリングパラダイムの核心に迫りました。

  • 第1章では、フローマッチングの基本的なアイデアと、拡散モデルとの関係性を概観しました。
  • 第2章では、フロー、速度場、ODE、プッシュフォワード、連続の方程式といった、FMを支える数学的基盤を整理しました。
  • 第3章では、FMの学習アルゴリズムの核心である「周辺化トリック」と、最適輸送に動機付けられた線形条件付きフローの重要性を学びました。
  • 第4章では、FMをリーマン多様体という複雑な幾何学的空間へ拡張し、測地線フローやプレメトリックフローといった概念に触れました。
  • 第5章では、FMを離散状態空間へと拡張する離散フローマッチング（DFM）と、そのための因子化パスや混合パスのアイデアを見ました。
  • 第6章では、FMを究極的に一般化するジェネレータマッチング（GM）という統一的枠組みを導入し、任意のデータとマルコフ過程を扱える可能性を探りました。
  • 第7章では、FM/GMと拡散モデル（DDM）の関係性を詳細に比較し、両者がどのように共通の原理を共有しつつ、FM/GMがより柔軟な設計を可能にするのかを理解しました。

フローマッチングは、ソース分布からターゲット分布への連続的な変換を学習するという、直感的でありながら強力なアイデアに基づいています。シミュレーションフリーな学習、柔軟な確率パス設計、多様なデータモダリティへの適用可能性といった利点から、画像、動画、音声、テキスト、さらには科学的発見に至るまで、幅広い分野での応用が進んでいます。

本記事が、読者の皆様にとってフローマッチングという魅力的な世界への第一歩となり、Meta AIのガイドや関連論文を読み解く上での助けとなれば幸いです。生成AIの旅はまだ始まったばかりです。フローマッチングが切り拓く新たな可能性を、ぜひご自身の目で確かめてみてください。

関連リソース

記事

  • 要約：Flow Matching for Generative Modeling (Part 1)
    Qiita 記事。定理の証明を含め FM の数理を日本語で丁寧に整理し、実装イメージを掴みやすくしてくれる。(qiita.com)
  • Optimal Transport Conditional Flow Matching – 拡散モデルに取って代わる次世代の生成技術？
    OT-CFM を図解付きで紹介する日本語 Zenn 記事。条件付き生成まで扱う応用視点が充実。(zenn.dev)

論文

  • Flow Matching for Generative Modeling
    FM の原点論文。シミュレーション不要のベクトル場回帰で CNF を学習し、OT 経路で高速化・高品質生成を実現する方針を提案。(arxiv.org)
  • Flow Straight and Fast: Learning to Generate and Transfer Data with Rectified Flow
    “直線フロー”を学習して 1-step 生成に迫る高速変種。FM の速度場を直線経路に制限する利点と理論的根拠を解説。(arxiv.org)
  • Discrete Flow Matching
    高次元離散データ（コード生成など）に FM を拡張。確率経路スケジューラと大規模モデル実験で離散拡散との差を検証。(arxiv.org)
  • Generator Matching: Generative modeling with arbitrary Markov processes
    FM／拡散モデルを包括する GM の提案。無限小生成作用素を直接回帰し、ジャンプ過程のスーパー ポジションで多モーダル生成と性能向上を実証。(arxiv.org)
  • α-Flow: A Unified Framework for Continuous-State Discrete Flow Matching Models
    情報幾何に基づき CS-DFM を統一し、一般化運動エネルギー最小化の観点を提示する最新理論。(arxiv.org)

Youtube 動画

  • 【AI論文解説】Consistency ModelsとRectified Flow ~解説編Part1~
    Consistency Models と Rectified Flow に関する最新の研究動向を、スライドとともに解説した動画。理論的背景や実装のポイントを視覚的に整理。（youtube.com）
  • How I Understand Flow Matching
    ホワイトボード形式で FM と拡散モデルの関係を直感的に可視化し、要点をスッキリ整理。初心者向け。(youtube.com)

実装チュートリアル

  • facebookresearch/flow_matching
    本記事で扱ったMeta AIの「Flow Matching Guide and Code」(arXiv.org) の公式 PyTorch 実装。連続／離散 FM の学習・サンプリングスクリプトと画像／テキストのデモを収録。(github.com)
  • MIT 6.S184 “Flow & Diffusion Models” オンライン教材
    FM／拡散モデルを体系的に学べる講義ノート＋ Colab 演習。数式とコードを往復しながら手を動かせる。(diffusion.csail.mit.edu)

Discussion