🐡
論文紹介:Difference-in-Differences Designs: A Practitioner's Guide　Part1

stochi
2025/07/08に公開
!これはAIではなく、人が書いたブログです。基本的には論文で用いられている言葉・文章を日本語にしています。

これは論文のまとめ記事なのですが、論文を一通り目を通すことをおすすめします。

 論文の概要https://arxiv.org/abs/2503.13323
Difference-in-Differences Designs: A Practitioner's Guideは、社会科学における因果効果の推定で広く使われる「差分の差分法（Difference-in-Differences, DID）」について、実践者向けにその考え方と応用を解説する論文です。
特に、従来の2期間・2グループという単純なケースを超えて、複数の期間や、異なるタイミングで処置が導入されるStaggered treatmentといった、より複雑な現実のデータにDIDを適用する際の課題と、その解決策について説明しています。
論文の中心的な主張は、複雑なDID分析も、基本的な「2期間・2グループ」の分析の組み合わせ（building blocks）として理解できるという点です。この考え方に基づき、明確な因果関係の解釈が可能な推定方法を構築するフォワード・エンジニアリングアプローチを提案しています。

この論文を三つのブログに分けて紹介していく予定です。本ブログはそのPart1となります。
メディケイド拡大と死亡率
この論文では、議論を具体的にするために、一貫して以下の例が用いられます。

研究課題: 低所得者向けに医療費を援助するメディケイドの拡大が、死亡率にどのような影響を与えたか？

分析の特徴:

Staggered treatment: メディケイド拡大は、州によって開始年が異なります。（2014年から2023年にかけて段階的に導入）

データ: 郡レベルの死亡率データ（2009年〜2019年）を使用します。

課題: どのグループを比較対象とするか、地域差などの共変量をどう扱うか、といった分析上の選択が重要になります。


 2\times2 DID designsまず、DIDの最も基本的な形である「2期間・2グループ」のデザインについて説明します。

2グループ: 処置を受けるグループ（処置群）と、受けないグループ（対照群）

2期間: 処置が導入される前の期間（処置前）と、導入された後の期間（処置後）
メディケイドの例で言えば、以下のような状況です。

処置群: 2014年にメディケイドを拡大した州の郡

対照群: 2019年まで拡大しなかった州の郡

処置前: 2013年

処置後: 2014年
DIDの推定値は、「処置群での処置前後の変化」から「対照群での処置前後の変化」を差し引くことで計算されます。この背景には、「もし処置がなければ、処置群と対照群の死亡率のトレンドは同じだったはずだ（平行トレンド仮定）」という重要な仮定があります。

 Causal effects and target parameters: The ATTDIDで何を推定したいのかを明確にするため、Potential Outcomesという考え方を使います。

Y_{i,t}(1): ユニット（この例では郡）iが、時点tで処置を受けた場合の潜在的な結果

Y_{i,t}(0): ユニットiが、時点tで処置を受けなかった場合の潜在的な結果
現実には、あるユニットがある時点で処置を受けるか受けないかのどちらか一方しか観測できません。観測される結果Y_{i,t}は、以下の式で表されます。

Y_{i,t} = (1 - D_{i})Y_{i,t}(0) + D_{i}Y_{i,t}(1)

Y_{i,t}: 郡iの時点tにおける、実際に観測された死亡率

D_{i,t}: 処置の有無を示す変数。処置群で処置後の期間は1、それ以外は0となります
処置を受けなかった場合(D_{}=0)はY_{i,t}(0)となり、処置を受けた場合(D_{i}=1)はY_{i,t}(1)となることを示しています

 No-Anticipation Assumption
DIDを正しく適用するための重要な仮定として、No-Anticipationがあります。これは、「処置が実施されるより前の時点では、処置の効果は現れない」という仮定です。例えば、メディケイド拡大が2014年に発表・実施されるとして、その発表によって2013年の死亡率が変化するようなことがない、ということを意味します。

 処置群における平均処置効果 (ATT)
DIDが推定しようとする中心的な目標は、処置を受けたグループにおける平均的な処置の効果です。これは以下の数式で定義されます。

ATT(t) = \mathbb{E}[Y_{i,t}(1) - Y_{i,t}(0) | D_i = 1]
この式は、以下のように変形できます。

ATT(t) = \mathbb{E}[Y_{i,t} | D_i = 1] - \mathbb{E}[Y_{i,t}(0) | D_i = 1]

ATT(t): 時点tにおける処置群の平均処置効果。

\mathbb{E}[\cdot | D_i = 1]: 処置群（D_i=1）における期待値を取ることを意味します

第1項 \mathbb{E}[Y_{i,t} | D_i = 1]: 処置群で実際に観測された死亡率の期待値です。これはデータから計算できます

第2項 \mathbb{E}[Y_{i,t}(0) | D_i = 1]: 処置群が「もし処置を受けなかったとしたら、どうなっていたか」という死亡率の期待値です。これは現実には観測できない反実仮想です
DIDの本質は、この観測できない第2項を、対照群のデータを使ってうまく推定することにあります。この論文では、ATTを推定する際に、単純な平均を取るか、人口などで重み付け（加重）した平均を取るかによって、推定されるパラメータの意味合いが変わる点も指摘しています。

 Identifying assumptions: Parallel trends前のセクションで、処置群の平均処置効果（ATT）を推定するには、観測不可能な反実仮想 \mathbb{E}[Y_{i,t}(0) | D_i = 1]（もし処置群が処置を受けなかった場合の死亡率の期待値）を特定する必要があることを見ました。DIDでは、これを平行トレンド仮定：Parallel Trends Assumptionを用いて特定します。

 仮定 PT（Parallel Trends） (2×2 平行トレンド)
処置がない場合、処置群と対照群における潜在的結果 Y_{i,t}(0) の平均的な変化は同じである、という仮定です。

\mathbb{E}_{\omega}[Y_{i,t=2}(0) | D_i=1] - \mathbb{E}_{\omega}[Y_{i,t=1}(0) | D_i=1] = \mathbb{E}_{\omega}[Y_{i,t=2}(0) | D_i=0] - \mathbb{E}_{\omega}[Y_{i,t=1}(0) | D_i=0]

\mathbb{E}_{\omega} は、重み \omega を考慮した期待値を意味します。

左辺: 処置群において、「もし処置がなかったとしたら」、時点2と時点1の間で死亡率がどれだけ変化したか、という平均変化量です。これは観測できません。

右辺: 対照群において、時点2と時点1の間で死亡率がどれだけ変化したか、という平均変化量です。対照群は処置を受けていないので、これはデータから観測できます。
この仮定は、「処置群で観測できなかった『もしも』の変化は、対照群で実際に観測された変化と同じである」と仮定することを意味します。この仮定が成り立つと、観測できない反実仮想を以下のように計算できます。

\mathbb{E}_{\omega}[Y_{i,t=2}(0) | D_i=1] = \mathbb{E}_{\omega}[Y_{i,t=1}(0) | D_i=1] + (\mathbb{E}_{\omega}[Y_{i,t=2} | D_i=0] - \mathbb{E}_{\omega}[Y_{i,t=1} | D_i=0])
メディケイドの例でいえば、処置群の処置後の反実仮想（左辺）は、「処置群の処置前の死亡率」に「対照群で観測された死亡率の時間変化」を足し合わせることで推定できるということを示しています。これらの式を組み合わせることで、ATTを完全に観測可能なデータだけで表現できます。これがDIDの推定量です。

\begin{align*}
ATT(2014) &= \mathbb{E}_{\omega}[Y_{i,2014}(1)|D_i=1] - \mathbb{E}_{\omega}[Y_{i,2014}(0)|D_i=1]\\
&= \overbrace{\mathbb{E}_{\omega}[Y_{i,2014}|D_i = 1]}^{=\mathbb{E}_{\omega}[Y_{i,2014}(1)|D_i=1]} - \overbrace{(\mathbb{E}_{\omega}[Y_{i,2013}|D_i = 1] + (\mathbb{E}_{\omega}[Y_{i,2014}|D_i = 0] - \mathbb{E}_{\omega}[Y_{i,2013}|D_i = 0]))}^{=\mathbb{E}_{\omega}[Y_{i,2014}(0)|D_i=1]} \\
&= \underbrace{(\mathbb{E}_{\omega}[Y_{i,2014}|D_i = 1] - \mathbb{E}_{\omega}[Y_{i,2013}|D_i = 1])}_{\text{(weighted) average change for } D_i=1} - \underbrace{(\mathbb{E}_{\omega}[Y_{i,2014}|D_i = 0] - \mathbb{E}_{\omega}[Y_{i,2013}|D_i = 0])}_{\text{(weighted) average change for } D_i=0}
\end{align*}

 Estimation and inference: Four means or one regression?
 手計算によるDID
前セクションで紹介したATTは4つのグループ平均を計算して差を取ることで、ATTを推定できます。

\widehat{ATT}(2014) = (\bar{Y}_{\omega,D=1,t=2014} - \bar{Y}_{\omega,D=1,t=2013}) - (\bar{Y}_{\omega,D=0,t=2014} - \bar{Y}_{\omega,D=0,t=2013})
Table 2 には、この計算が具体的に示されています。


非加重（Unweighted）の場合: 処置群の変化は +9.3、対照群の変化は +9.1。その差（DID推定量）は +0.1となります。これは「メディケイド拡大は、拡大した『郡』の死亡率を10万人あたり0.1人増加させた」と解釈されますが、統計的に有意ではありません。

加重（Weighted）の場合: 処置群の変化は +3.7、対照群の変化は +6.3。その差（DID推定量）は-2.6となります。これは「メディケイド拡大は、拡大州の『住民』の死亡率を10万人あたり2.6人減少させた」と解釈でき、統計的に有意です。

 回帰分析によるDID
DIDは、以下の回帰モデルを最小二乗法（OLS）で推定することでも得られます。

Y_{i,t} = \beta_0 + \beta_1 \mathbf{1}\{D_i=1\} + \beta_2 \mathbf{1}\{t=2014\} + \beta_{2 \times 2} (\mathbf{1}\{D_i=1\} \times \mathbf{1}\{t=2014\}) + \epsilon_{i,t}

Y_{i,t}: 郡iの時点tにおける死亡率。

\mathbf{1}\{D_i=1\}: 処置群ダミー（処置群なら1、そうでなければ0）。

\mathbf{1}\{t=2014\}: 処置後ダミー（2014年なら1、そうでなければ0）。

\mathbf{1}\{D_i=1\} \times \mathbf{1}\{t=2014\}: 交互作用項。処置群かつ処置後の場合にのみ1になります。
このモデルでは、交互作用項の係数 \boldsymbol{\beta_{2 \times 2}} が、DID推定量（ATT）と一致します。

\epsilon_{i,t}: 誤差項
このモデルから得られる4つの平均値は以下のように表現できます：
処置群の処置後（2014年）の平均: Y_{D=1,t=2014} = \hat{\beta_0} + \hat{\beta_1} + \hat{\beta_2} + \hat{\beta_{2 \times 2}}
処置群の処置前（2013年）の平均: Y_{D=1,t=2013} = \hat{\beta_0} + \hat{\beta_1}
対照群の処置後（2014年）の平均: Y_{D=0,t=2014} = \hat{\beta_0} + \hat{\beta_2}
対照群の処置前（2013年）の平均: Y_{D=0,t=2013} = \hat{\beta_0}
これらの式を\widehat{ATT}の定義に代入すると：
\widehat{ATT}(2014) = [(\hat{\beta_0} + \hat{\beta_1} + \hat{\beta_2} + \hat{\beta_{2 \times 2}}) - (\hat{\beta_0} + \hat{\beta_1})] - [(\hat{\beta_0} + \hat{\beta_2}) - \hat{\beta_0}] = \hat{\beta_{2 \times 2}}
となります。
Table 3 は、この回帰分析の結果を示しており、手計算の結果と一致することを確認できます。


 Incorporating covariates into 2×2 DIDこれまでの議論では、処置群と対照群を直接比較してきましたが、実際にはこれらのグループ間で元々特性が異なる場合があります。例えば、メディケイドを拡大した州とそうでない州では、貧困率や人種構成が元から異なっているかもしれません。このような共変量の違いが、処置がなくても死亡率のトレンドに影響を与える可能性があります。
このセクションでは、共変量を分析に組み込むこんだDID分析について紹介しています。

 Covariate balance: Is unconditional parallel trends plausible?DID分析を行う前段階として、処置群と対照群が処置開始前にどれだけ似ているかを確認するバランスチェックが非常に重要です。そこで正規化差を用います。正規化差は、単位に依存せず、変数のばらつきを考慮したグループ間の差を示す指標です。

 正規化差の計算式
\text{Norm. Diff.} = \frac{\bar{X}_{\omega,T} - \bar{X}_{\omega,C}}{\sqrt{(S^2_{\omega,T} + S^2_{\omega,C})/2}}

\bar{X}_{\omega,T}: 処置群（Treatment group）における共変量の（加重）サンプル平均。

\bar{X}_{\omega,C}: 対照群（Comparison group）における共変量の（加重）サンプル平均。

S^2_{\omega,T}: 処置群における共変量の（加重）サンプル分散。

S^2_{\omega,C}: 対照群における共変量の（加重）サンプル分散。
この式の構造を分解してみましょう。

分子 (\bar{X}_{\omega,T} - \bar{X}_{\omega,C}):
これは処置群と対照群の平均値の差です。単純な差であり、これが正規化の対象となります。


分母 (\sqrt{(S^2_{\omega,T} + S^2_{\omega,C})/2}):
これは処置群と対照群の標準偏差をプールしたものです。
まず、両群の分散 (S^2) を平均しています。これにより、両群のばらつきを総合的に考慮します。
この分母は、その共変量が平均的にどれくらいばらついているかを示す指標となります。

つまり、正規化差は「両群の平均値の差が、プールされた標準偏差の何倍あるか」を示しています。正規化差の絶対値が 0.25 を超える場合、グループ間に潜在的に問題となる不均衡が存在する可能性を示唆します。これはあくまで経験則であり、絶対的な基準ではないみたいです。
論文のTable 4では、この正規化差が実際に計算されています。

上段 (2013 Covariate Levels):
例えば「Unemployment Rate」の非加重（Unweighted）の正規化差は0.16です。これは、拡大州と非拡大州の2013年時点での失業率の平均値の差が、プールされた標準偏差の0.16倍であることを意味します。この値は0.25より小さいので、大きなインバランスとは見なされないかもしれません。
一方、Median Incomeの正規化差は0.43です。これは0.25を大きく超えており、処置前に両群間で所得レベルに無視できない差があったことを示唆しています。


下段 (2013-14 Covariate Differences):
ここでは、共変量の変化量について正規化差を計算しています。
例えば、Unemployment Rateの変化量の正規化差は-0.21です。これは、2013年から2014年にかけての失業率の変化が、両群でやや異なっていたことを示します。

このように正規化差を計算することで、処置群と対照群の比較する際に、どの共変量が問題になる可能性があるかを評価する材料となります。
Table 4 は、メディケイドの例における共変量のバランスを示しています。


 DID with covariates: Identification under conditional parallel trends共変量のインバランスがある場合、より弱い仮定である条件付き平行トレンド仮定：Conditional Parallel Trends, CPTを用います。

 仮定 CPT (2×2 条件付き平行トレンド)同じ共変量の値を持つ処置ユニットと比較ユニット間で、Y_{i,t}(0)の（重み付き）平均的変化が同じであるという仮定です。

\mathbb{E}_{\omega}[Y_{i,t=2}(0) - Y_{i,t=1}(0) | X_i, D_i = 1] = \mathbb{E}_{\omega}[Y_{i,t=2}(0) - Y_{i,t=1}(0) | X_i, D_i = 0] 
仮定CPTは仮定PTと同じ構造を持ちますが、PTが全人口・ユーザーに対して成り立つのに対し、CPTは各共変量固有の層（covariate-specific stratum）内で成り立つと仮定します。
メディケイド例での解釈： Table 4のベースライン共変量に関して、この仮定は2013年時点で同じ女性・白人・ヒスパニック比率、失業率・貧困率・所得中央値を持つ拡大郡と非拡大郡間で、Y_{i,t}(0)の平行トレンドを仮定することを意味します。
CPTは、共変量固有のトレンドが拡大郡と非拡大郡で共通であることのみを要求します。

 仮定 SO (Strong Overlap)未処置潜在アウトカム成長の決定要因である観測共変量X_iが与えられたときの処置群に属する条件付き（重み付き）確率は、0と1から一様に離れています。すなわち、ある\epsilon > 0に対して、\epsilon < P_{\omega}[D_i = 1|X_i] < 1 - \epsilonです。
仮定CPTの両方の期待値が全てのX_iの値に対して適切に定義されるためには、各共変量値において処置ユニットと未処置ユニットの両方が存在しなければなりません。もしある共変量値に対して処置ユニットのみが存在する場合、\mathbb{E}_{\omega}[Y_{i,t=2}(0) - Y_{i,t=1}(0) | X_i, D_i = 0]は未定義となります。

 ATT(2)の識別仮定CPTとSOの下で、ATT(2)は識別されます：

ATT(2) = \mathbb{E}_{\omega}[Y_{i,t=2}(1)|D_i = 1] - \mathbb{E}_{\omega}[Y_{i,t=2}(0)|D_i = 1]

= \mathbb{E}_{\omega}[Y_{i,t=2}|D_i = 1] - \mathbb{E}_{\omega}[\mathbb{E}_{\omega}[Y_{i,t=2}(0)|X_i, D_i = 1]|D_i = 1]

= \mathbb{E}_{\omega}[Y_{i,t=2}|D_i = 1] - \mathbb{E}_{\omega}[\mathbb{E}_{\omega}[Y_{i,t=1}(0)|X_i, D_i = 1] + \mathbb{E}_{\omega}[\Delta Y_{i,t=2}(0)|X_i, D_i = 0]|D_i = 1]

= \mathbb{E}_{\omega}[\Delta Y_{i,t=2}|D_i = 1] - \mathbb{E}_{\omega}[\mathbb{E}_{\omega}[\Delta Y_{i,t=2}|X_i, D_i = 0]|D_i = 1]

第1行： ATT(2)の定義を再記述

第2行： 繰り返し期待値の法則を用いて、処置群全体の反実仮想平均をX_iに条件づけた反実仮想平均の平均として記述

第3行： 仮定CPTを用いて、反実仮想を予期なし仮定（Assumption NA）の下での観測可能な人口量として書き直し

第4行： 再度繰り返し期待値の法則を用いて項をグループ化し、ATT(2)を観測変数(Y_{i,t=2}, Y_{i,t=1}, G_i, X_i)の観点から表現
ATT(2)は処置群が経験したアウトカムの変化（左辺の項）から、各共変量値に対する比較群のアウトカム変化を処置群の共変量分布で平均したもの（右辺の項）を差し引いた値に等しいということです。

 DID estimation with covariates: TWFE基本的なDID分析から一歩進んで、共変量（分析対象の個人や地域が持つ、介入以外の特性。例：年齢、性別、所得など）を考慮に入れるこんだDID分析について紹介しています。しかし、共変量が連続変数であったり、数が多かったりすると、単純なグループ分けと平均値の比較では対応が難しくなります。そのため、実務では回帰分析を用いるのが一般的です。特に、TWFEモデルは簡単で馴染み深いため、非常によく使われます。

 TWFEモデルの基本形典型的なTWFEの回帰モデル式は以下のように表されます。

Y_{i,t} = \theta_t + \eta_i + \beta_{treat} D_{i,t} + X'_{i,t} \beta_{covs} + e_{i,t}

Y_{i,t}: 個人 i の時点 t における結果変数（例：死亡率）

\theta_t: 時間固定効果。すべての個人に共通する時点t特有の影響（例：その年の景気動向）を捉えます

\eta_i: 個人固定効果。時間を通じて変化しない個人i特有の特性（例：性別）を捉えます

D_{i,t}: 処置の有無を示す変数。処置群で処置後の期間は1、それ以外は0となります

\beta_{treat}: 推定したい係数。処置が結果に与える平均的な効果ATTと解釈されます

X'_{i,t}: 時間によって変化する可能性のある共変量のベクトル（例：失業率、人口構成）

\beta_{covs}: 共変量が結果に与える影響を示す係数ベクトル

e_{i,t}: 誤差項
時間とともに変化する共変量 X_{i,t} の代わりに、処置前のベースライン時点（t=1）の共変量と 処置後の時間ダミー（t=2）を掛け合わせた交互作用項を用いるモデルもあります。

Y_{i,t} = \theta_t + \eta_i + \beta_{treat,2} D_{i,t} + (1\{t=2\} \cdot X'_{i,t=1}) \beta_{covs,2} + e_{i,t}
このモデルは、共変量のベースラインでの値が、介入後の結果のトレンドにどう影響するかをコントロールしようとするものです。1\{t=2\}は時点 t が2のときだけ1になるダミー変数です。
論文では米国のメディケイド拡大が死亡率に与えた影響を共変量を入れて分析した例を紹介しています。表5
上記のようにどの共変量をどのようにモデルに含めるかによって、推定結果が大きく変わってしまうこともあります。したがって、回帰分析で推定された係数 \beta_{treat} は、本当に我々が知りたい因果効果を正しく捉えているのか？という根本的な疑問が残ります。

 TWFEモデルの問題点と解釈の難しさTWFEモデルは実務でよく使われる一方で、重要な理論的課題を抱えています。特に、共変量を組み込むと、推定係数\betaが我々が本当に知りたい平均処置効果\text{ATT}(2)を正しく識別できなくなる場合が多いです。論文では、なぜ\betaと\text{ATT}(2)が異なってしまうのかについて説明しています。

 TWFEの2つのモデルTWFEモデルには、共変量の扱い方によって主に2つの形式があります。どちらを選ぶかによって、何をコントロールしているのかが大きく変わってきます。
モデル1：

\Delta Y_{i,t=2} = \alpha + \beta_{\text{treat}} D_i + \Delta X'_{i,t=2}\beta_{\text{covs}} + \Delta e_{i,2}

基本的な考え方：各観測単位について、期間1から期間2への変化量を直接分析する

主な特徴：時間不変変数（個人固定効果\eta_i）が自動的に消える
モデル2：

\Delta　Y_{i,t=2} = \alpha + \beta_{\text{treat},2} D_i + X'_{i,t=1}\beta_{\text{covs},2} + \Delta e_{i,2}

基本的な考え方：ベースライン時点（t=1）の共変量値が、その後のトレンドに与える影響をコントロール

主な特徴：ベースライン特性を保持し、それらが時間経過とともに結果変数に与える異質的な影響を調整
この2つのモデルの違いをまとめると以下のような感じになると思います。貧困率をコントロールしたいと考えた場合：
モデル1の場合：貧困率の変化（\Delta貧困率）をコントロール
例：「2013年から2014年にかけて貧困率が3%上昇した地域」の効果をコントロール
モデル2の場合：ベースライン貧困率（2013年時点）をコントロール
例：「2013年時点で貧困率が20%だった地域」の効果をコントロール
同じ貧困率をコントロールでも、実際には全く異なる要因をコントロールしており、推定結果も大きく変わる可能性があります。

 TWFEモデルの根本的問題TWFEで推定される\beta_{\text{treat}}が、真の因果効果ATT(2)と一致するためには、非常に強い仮定が必要です。具体的には、処置効果が\Delta X_{i,2}によって変化しないことが必要となります。
共変量の変化\Delta Xで条件付けた処置効果を\text{ATT}_{\Delta X_{i,t=2}}(2)として以下のように定義します：
\text{ATT}_{\Delta X_{i,t=2}}(2)= E[Y_{i,2}(1) - Y_{i,2}(0)|D_i = 1,\,\Delta X_{i,t=2}]条件付き平行トレンドとStrong Overlapが成り立つと仮定すると：

\begin{align*}
\text{ATT}_{\Delta X_{i,t=2}}(2) 
&= E[\Delta Y_{i,2}|D_i = 1,\,\Delta X_{i,t=2}] -  E[\Delta Y_{i,2}|D_i = 0,\,\Delta X_{i,t=2}]\\
&= (\beta_{\text{treat}}+\Delta X'_{i,t=2}\beta_{\text{covs}})-(\Delta X'_{i,t=2}\beta_{\text{covs}}) \\
&= \beta_{\text{treat}}
\end{align*}
この計算から分かるように、\beta_{\text{treat}} = \text{ATT}(2)となるためには、介入・処置効果が共変量層にわたって一定である必要があります。しかし現実には、介入・処置効果が共変量層間で異なることが一般的です。

 共変量コントロールがもたらす具体的なリスク共変量を不適切にモデルに含めることで、以下のような問題が生じる可能性があります。
1. 時間不変変数の脱落
モデル1では\Delta X_{i,2} = X_{i,2} - X_{i,1}を用いるため、時間で変化しない要因は自動的に消去されます。この結果、介入前の特性（ベースライン）が異なるグループが、時間とともに異なるトレンドを示す可能性を適切にコントロールできなくなります。
例えば、メディケイド拡大研究において、各州の恒常的な医療リソース格差は差分で消えてしまうため、これらが死亡率トレンドに与える影響を直接コントロールできません。
2. Bad Controls問題
処理自体が共変量Xを変化させる場合、その変化後のXをコントロール変数として含めると、真の処理効果の一部がXの係数に吸収され、\betaにバイアスが生じます。
例えば、メディケイド拡大が貧困率を下げる効果があるとき、拡張後（2014年）の貧困率や2013-2014年の貧困率変化をコントロールに含めると、メディケイド拡大の真の効果を過小評価してしまいます。
3. 重み付けと符号逆転の問題（Caetano & Callaway 2024）
TWFEの最も深刻な問題は、推定される\beta係数が非凸重み付き平均となることです。

各共変量層での条件付き平均処理効果：
\text{ATT}_{X_k}(2) = E\!\left[Y_{i,2}(1) - Y_{i,2}(0)\;\big|\;D_i = 1,\,X_i = x_k\right]\betaはこれらの重み付き平均となりますが、その重みが凸ではないため、重みが負になることもあり、各共変量ごとのATTが正でも\betaが負になる可能性があります。（重み付けの詳細については、Caetano and Callaway (2024) を参照してください。）
このように、TWFEモデルは便利である一方で、多くの落とし穴があることが分かります。次のセクションでは代替的手法について解説されています。

 DID estimators with covariates that target the ATT(2)
ATT(2) = E_\omega[\Delta Y_{i,t=2}|D_i = 1] - E_\omega \left[ E_\omega[\Delta Y_{i,t=2}|X_i, D_i = 0]|D_i = 1 \right]
この式は、介入グループの実際の変化（第1項）から、介入グループが非介入だった場合の条件付き期待値（第2項）を差し引いた形になっています。第1項は標準的な2×2デザインと同じで、サンプル平均 (\bar{Y}_{\omega,D=1,t=2} - \bar{Y}_{\omega,D=1,t=1}) で置き換えることができます。
ここで紹介する3つの手法（RA、IPW、DR）は、いずれも条件付き並行トレンド仮定CPTとSOの下で、第2項をどのように推定するかによって区別されます。

 1. 回帰調整（Regression Adjustment, RA）アプローチRAアプローチは、非介入グループの結果変化パターンを直接モデル化して、介入グループの反実仮想を予測する手法です。
推定手順：
ステップ1: 非介入グループ（D_i=0）のデータのみを使って、結果の変化 \Delta Y を共変量 X_i に回帰させるモデル\mu_{\omega,\Delta,D=0}(X_i) を推定します。実際の応用では線形回帰 \mu_{\omega,\Delta,D=0}(X_i) = X_i'\beta_{D=0} がよく使われます。
ステップ2: 推定したモデルを使って、すべての個人（介入グループを含む）について予測値 \hat{\mu}_{\omega,\Delta,D=0}(X_i) = X_i'\hat{\beta}_{D=0} を計算します。
ステップ3: ATT(2)の識別式の第2項の内側の条件付き期待値 E_\omega[\Delta Y_{i,t=2}|X_i, D_i = 0] を推定された\hat{\mu}_{\omega,\Delta,D=0}(X_i) で置き換えます。
ステップ4: 第2項全体を以下のように推定します：

E_\omega \left[ E_\omega[\Delta Y_{i,t=2}|X_i, D_i = 0]|D_i = 1 \right] \approx E_\omega \left[ \hat{\mu}_{\omega,\Delta,D=0}(X_i)|D_i = 1 \right] = \frac{\sum_{i=1}^n D_i \omega_i \hat{\mu}_{\omega,\Delta,D=0}(X_i)}{\sum_{i=1}^n D_i \omega_i}
これは処置群の共変量値に対する予測値の加重平均、つまり処置群が非処置だった場合の予測される平均変化を表します。
ステップ5: 最終的なATT推定量は、第1項（介入グループの実際の平均変化）から第2項を引いて：

\widehat{ATT}_{ra}(2) = \frac{\sum_{i=1}^n D_i \omega_i \Delta Y_{i,t=2}}{\sum_{i=1}^n D_i \omega_i} - \frac{\sum_{i=1}^n D_i \omega_i \hat{\mu}_{\omega,\Delta,D=0}(X_i)}{\sum_{i=1}^n D_i \omega_i}
これを整理すると：

\widehat{ATT}_{ra}(2) = \frac{\sum_{i=1}^{n} D_i \omega_i (\Delta Y_{i,t=2} - \hat{\mu}_{\omega,\Delta,D=0}(X_i))}{\sum_{i=1}^{n} D_i \omega_i} 
処置グループの実際の変化（\Delta Y_{i,t=2}）から、対照群だった場合の予測変化（\hat{\mu}_{\omega,\Delta,D=0}(X_i)）を差し引いた値の加重平均が処置効果の推定値となります。
モデルが誤特定されている場合、結果として得られるRA推定量にバイアスが生じます。

 2. 逆確率重み付け（IPW）アプローチRAが結果をモデル化したのに対し、IPWは誰が処置を受けるかの確率（傾向スコア）をモデル化します。そして、この確率を使って非介入グループを重み付けし直し、介入グループと同じような特徴を持つ比較グループを作り出します。

介入グループと非介入グループで共変量の分布が異なる場合、単純に比較するとバイアスが生じます。そこで、非介入グループの中でも介入グループに似た特徴を持つ人により大きな重みを与えることで、バランスの取れた比較を実現します。
パネルデータが利用可能で、仮定CPTとSOの下で、以下のように表現できます：

ATT(2) = E\left[ \left( w_{\omega,D=1}(D_i) - w_{\omega,D=0}(D_i, X_i) \right) \Delta Y_{i,t=2} \right]
ここで、重みは以下のように定義されます：

w_{\omega,D=1}(D) = D\omega / E[\omega D], \quad \text{and} \quad w_{\omega,D=0}(D, X) = \frac{\omega(1-D)p_\omega(X)}{1-p_\omega(X)} / E\left[ \frac{\omega(1-D)p_\omega(X)}{1-p_\omega(X)} \right]
推定手順：
ステップ1: 全サンプルを使って、介入を受ける条件付き確率（傾向スコア）p_\omega(X_i) = P_\omega(D_i=1 | X_i) をモデル化します。実際にはロジスティック回帰 \pi_\omega(X_i) がよく使われ、最尤法で推定されます。
ステップ2: 推定された傾向スコア \hat{p}_\omega(X_i) を使って、サンプル版の重みを計算します：

\hat{w}_{\omega,D=1}(D) = D\omega / \frac{1}{n}\sum_{i=1}^n D_i\omega_i, \quad \hat{w}_{\omega,D=0}(D,X) = \frac{\omega(1-D)\hat{p}_\omega(X)}{1-\hat{p}_\omega(X)} / \frac{1}{n}\sum_{i=1}^n \frac{\omega_i(1-D_i)\hat{p}_\omega(X_i)}{1-\hat{p}_\omega(X_i)} 
ステップ3: これらの重みを使ってATTを推定します：

\widehat{ATT}_{ipw}(2) = \frac{1}{n} \sum_{i=1}^{n} (\hat{w}_{\omega,D=1}(D_i) - \hat{w}_{\omega,D=0}(D_i, X_i)) \Delta Y_{i,t=2} 
重みの直感的理解：w_{\omega,D=1}(D) は介入グループに対してのみ非ゼロで、単純に\omega重み付き平均となります。一方、w_{\omega,D=0}(D,X) は非介入グループに対してのみ非ゼロで、傾向スコアが高い（つまり介入グループに似ている）人ほど大きな重みが付きます。この特定の重み付け関数により、IPWは介入グループと共変量分布が一致する比較グループを構築できます。
IPWの課題と対策：
傾向スコア \hat{p}_\omega(X_i) が1に近いと、非介入グループの重み \hat{w}_{\omega,D=0}(D,X) が極端に大きくなり（ゼロで割ることになるため）、推定が不安定になります
実際には極端な傾向スコア（0.995以上など）を持つ観測値は除外（トリミング）することが推奨されます
下図のような傾向スコアの分布を確認し、介入・非介入グループ間で十分な重複があることを確認する必要があります
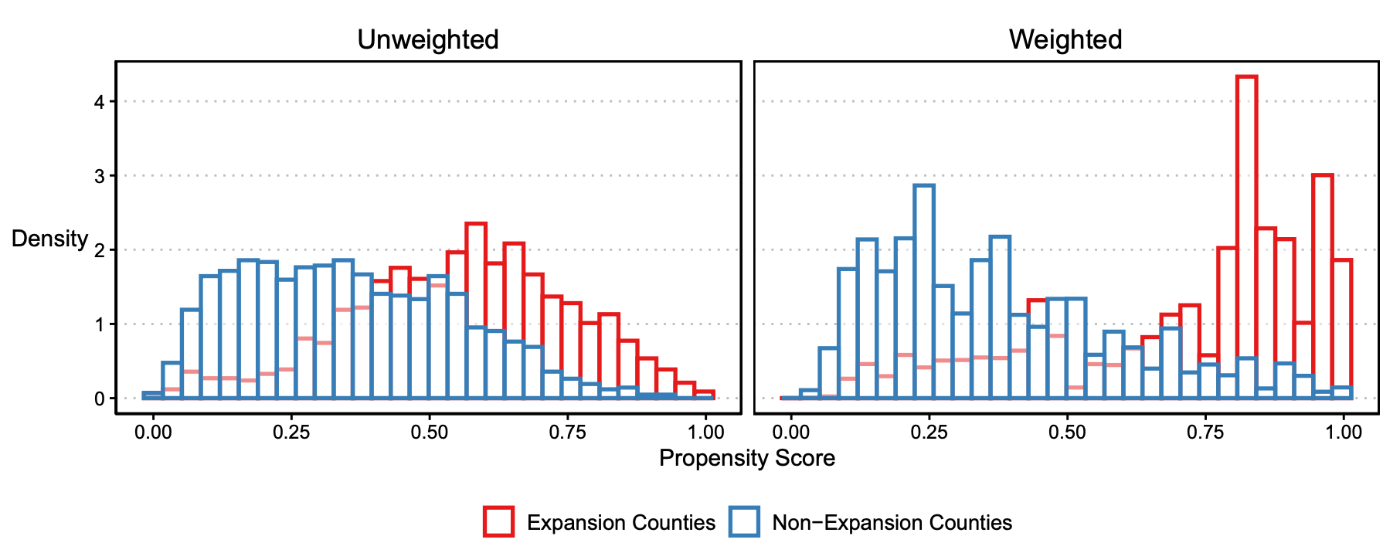
この図は、拡大州（赤）と非拡大州（青）の傾向スコア分布を示しています。対照群で極端に高い傾向スコアを持つ観測値が少なく、両グループの分布が良好に重複していることが確認できます。

 3. 二重に頑健な（Doubly Robust, DR）アプローチDRアプローチは、RAとIPWのいいとこ取りをした手法です。
基本的な発想：RAは結果モデルが正しければ有効、IPWは傾向スコアモデルが正しければ有効です。DRは両方のモデルを組み合わせることで、どちらか一方でも正しければOKという頑健性を実現します。

ATT(2) = E\left[ (w_{\omega,D=1}(D_i) - w_{\omega,D=0}(D_i, X_i)) (\Delta Y_{i,t=2} - E_\omega[\Delta Y_{i,t=2} | X_i, D_i=0]) \right]
この式は、IPWの重み付け構造（(w_{\omega,D=1}(D_i) - w_{\omega,D=0}(D_i, X_i))）に、RAで使った「残差」（実際の変化から条件付き期待値を引いたもの）を組み合わせた形になっています。
E_\omega[\Delta Y_{i,t=2}|X_i, D_i = 0] 項を省略すると、IPW推定量になります。逆に、w_{\omega,D=0}(D_i, X_i) 項を省略すると、RA推定量になります。
推定量：

\widehat{ATT}_{dr}(2) = \frac{1}{n} \sum_{i=1}^{n} (\hat{w}_{\omega,D=1}(D_i) - \hat{w}_{\omega,D=0}(D_i, X_i)) (\Delta Y_{i,t=2} - \hat{\mu}_{\omega,\Delta,D=0}(X_i))
ここで、\hat{w} はIPWで定義された推定重み、\hat{\mu} はRAで使った推定結果モデルです。
「二重に頑健」の意味：
結果モデル（\mu）が正しく特定されていれば、傾向スコアモデル（p）が間違っていても一致推定量が得られます
逆に、傾向スコアモデルが正しければ、結果モデルが間違っていても一致推定量が得られます
両方が少し間違っていても、それらの誤差が乗法的に作用し、DR推定量は（漸近的に）どちらか単独よりも良い性能を示します

 3つの手法の関係と実証結果Table 6の実証結果

以下の表は、Sant'Anna and Zhao (2020)およびCallaway and Sant'Anna (2021)の推定量に含まれる回帰・傾向スコアモデルの結果を報告しています。最初の2列は非重み付け回帰の結果を報告し、後の2列は重み付け回帰モデルの結果です。回帰モデルは、2014年にMedicaidを拡大しない1,222郡について、2013年の共変量値の関数として結果変数（死亡率）の変化を予測しています。傾向スコアモデルは2013年の全2,200郡のデータを使用し、2013年の共変量レベルに基づく拡大指示変数のロジットモデルを推定しています。標準誤差（括弧内）は郡レベルでクラスター化されています。

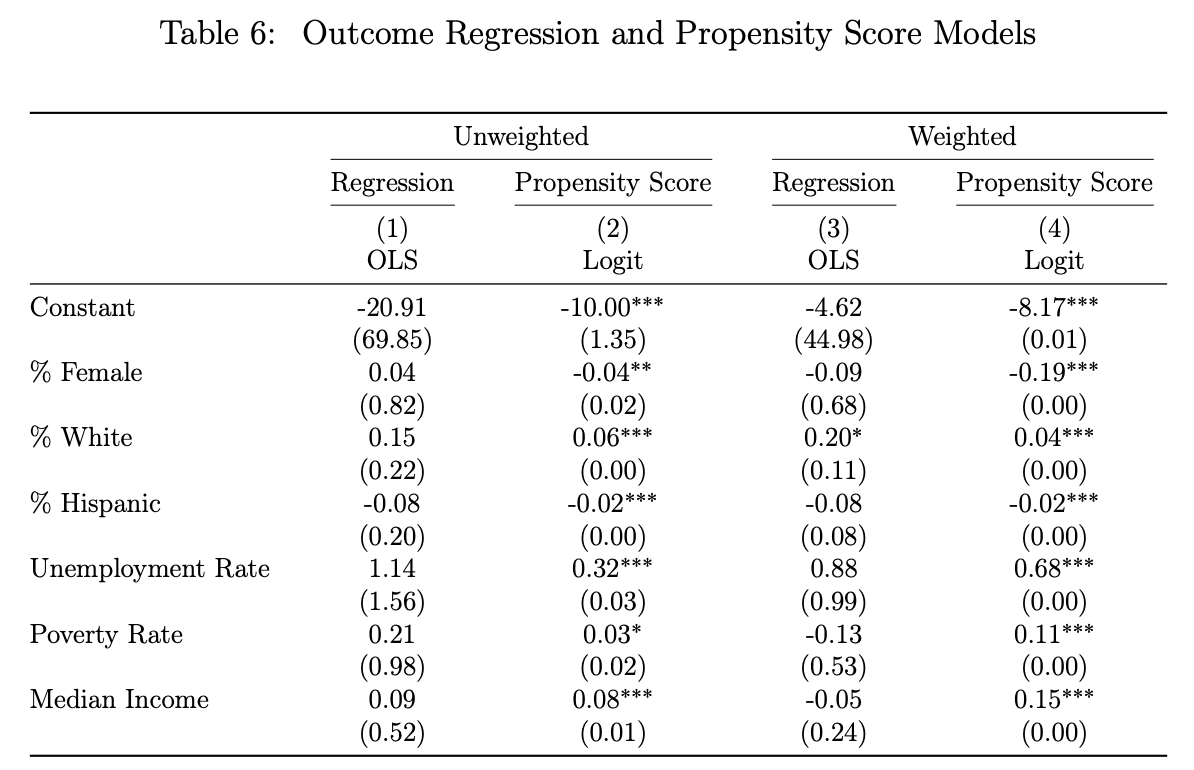
 列1,3の解釈：非拡大州における死亡率変化は基準共変量と弱い関係のみ
大部分の係数が統計的に有意でない→モデルが非介入結果トレンドをうまく説明できていない

 列2,4の解釈：多くの係数が統計的に有意
傾向スコアモデルが拡大決定をよく説明している
これは共変量は死亡率トレンドよりもMedicaid拡大をよく説明していると言えるのかなと思います。
Table 7の実証結果（Medicaid拡大の死亡率への影響）：

第1列は回帰調整を使用した結果を報告し、第2列は含まれる共変量を使用した傾向スコアモデルに基づく逆確率重み付けを使用し、第3列は2つのアプローチの二重に頑健な組み合わせを使用している。標準誤差（括弧内）は郡レベルでクラスター化されている。


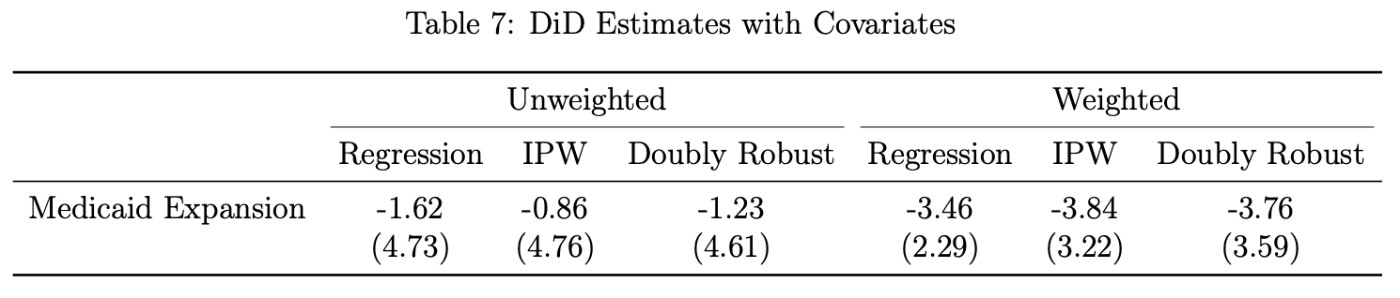
（解釈は表の通り。省略）

 Heterogeneity analysis共変量を使用する別の動機は、共変量の値 X_{it} によって処置効果がどのように異なるかを推定することです。

ATT(2) = E_\omega \left[ E_\omega[\Delta Y_{i,t=2}|X_i, D_i = 1] - E_\omega[\Delta Y_{i,t=2}|X_i, D_i = 0]|D_i = 1 \right]
仮定CPTとSOにより、条件付きATTパラメータを識別することもできます：

ATT_{X_i}(2) \equiv E_\omega[Y_{i,t=2}(1) - Y_{i,t=2}(0)|D_i = 1, X_i]

= E_\omega[\Delta Y_{i,t=2}|X_i, D_i = 1] - E_\omega[\Delta Y_{i,t=2}|X_i, D_i = 0]

 離散共変量の場合全ての共変量が離散的な場合、ATT_{X_i}(2) パラメータの推定は比較的簡単です。共変量のすべての可能な組み合わせによる層化（saturated partitions）x_k, k = 1, \ldots, K を行い、各層 k に属する単位のみを含むようにデータをサブセット化できます。
分割の具体例：

共変量が「性別（男性/女性）」と「教育レベル（高校以下/大学以上）」の2つの離散変数だとします。この場合、以下の4つの分割グループを形成できます：

x_1: 男性 × 高校以下

x_2: 男性 × 大学以上

x_3: 女性 × 高校以下

x_4: 女性 × 大学以上
各分割 k において、その特定の共変量の組み合わせを持つ個人のみでサブサンプルを作成し、そのサブサンプル内で標準的なDID分析を実行します。これにより、その特定の属性グループに対する処置効果 ATT_{x_k}(2) を推定できます。

 連続共変量または多数分割の場合一部の共変量が連続的であるか、層が非常に多く各層の観測値が少ない場合でも、ATT_{X_i}(2) を識別することは可能ですが、補助仮定なしには推定が困難です。
このような場合、ATT_{X_i}(2) よりもより集約された条件付きATTパラメータを識別・推定することが慣例です。例えば、失業率が中央値を上回る郡と下回る郡でMedicaid拡大の効果が異なるかを評価できます。
この層別ATTの概念を形式化するため、PART(X_i) をユーザー指定の共変量空間の分割とし、PART(X_i) \in \{1, 2, \ldots, K\} として、以下を定義します：

ATT_k(2) = E_\omega[Y_{i,t=2}(1) - Y_{i,t=2}(0)|D_i = 1, PART(X_i) = k]
仮定CPTとSOの下で、以下が成り立ちます：

ATT_k(2) = E_\omega[\Delta Y_{i,t=2}|D_i = 1, PART(X_i) = k]

- E_\omega \left[ E_\omega[\Delta Y_{i,t=2}|D_i = 0, X_i, PART(X_i) = k]|D_i = 1, PART(X_i) = k \right]
これにより、以下の集約関係が導かれます：

ATT(2) = \sum_{k=1}^K P_\omega(PART(X_i) = k|D_i = 1)ATT_k(2)

 最後に本ブログでは、DID分析の基礎である2×2デザインから、共変量を考慮した発展的な手法まで論文の前半部分について解説しました。
DID分析は一見シンプルに見えますが、実際の応用では多くの選択肢と注意点があることがわかったと思います。特に、共変量の扱い方や推定手法の選択によって結果が大きく変わる可能性があることを、メディケイド拡大の例を通じて確認しました。

Part2では、より複雑な設定におけるDID分析について解説します。