Zenn
🪐

量子カーネル SVM で遊んでみる — Qiskit

2022/10/18に公開
Python
機械学習
poem
Qiskit
tech

目的

カーネル SVM を眺めてみる で触れたように、Quantum feature maps and kernels を思いっきり劣化させることで、ブラックボックス度を低下させ、toy-problem なデータセットを解かせることで簡単なコンテンツを目指したい。

データセット

前回と同様に以下のデータセットを使いたい。

これは前回と同様に以下で訓練セット (train_data, train_labels) とテストセット (test_data, test_labels) が準備されているとする。

from sklearn.datasets import make_circles

X, Y = make_circles(n_samples=200, noise=0.05, factor=0.4)

A = X[np.where(Y==0)]
B = X[np.where(Y==1)]

A_label = np.zeros(A.shape[0], dtype=int)
B_label = np.ones(B.shape[0], dtype=int)

def make_train_test_sets(test_ratio=.3):
    def split(arr, test_ratio):
        sep = int(arr.shape[0]*(1-test_ratio))
        return arr[:sep], arr[sep:]

    A_label = np.zeros(A.shape[0], dtype=int)
    B_label = np.ones(B.shape[0], dtype=int)
    A_train, A_test = split(A, test_ratio)
    B_train, B_test = split(B, test_ratio)
    A_train_label, A_test_label = split(A_label, test_ratio)
    B_train_label, B_test_label = split(B_label, test_ratio)
    X_train = np.concatenate([A_train, B_train])
    y_train = np.concatenate([A_train_label, B_train_label])
    X_test = np.concatenate([A_test, B_test])
    y_test = np.concatenate([A_test_label, B_test_label])
    return X_train, y_train, X_test, y_test

train_data, train_labels, test_data, test_labels = make_train_test_sets()

カーネル法

再度重要な式を掲載すると、データセット \{ \xi_i \} の属する空間 \Omega と 実際に問題を解きたい高次元の空間 \mathcal{H}、そしてそれらを結ぶ特徴写像 \Phi: \Omega \to \mathcal{H} があるとして、\mathcal{H} が大変良い性質を持っている場合には、カーネル関数と呼ばれる k: \Omega \times \Omega \to \R なる関数がとれて

\begin{align*} \braket{\Phi(\xi_i), \Phi(\xi_j)} = k(\xi_i, \xi_j) \tag{1} \end{align*}

と書けるのであった。

また、カーネル SVM を眺めてみる#自作カーネルを用いる で触れたように、データセット内のデータ同士の類似度からなるような自作カーネルを表す行列 — 例えばグラム行列 (k(\xi_i, \xi_j))_{1 \leq i,j \leq n} — を用いてカーネル SVM の計算ができることを見た。

今回のデータセットの場合、\phi を明示的に与えてグラム行列を作ることができることも既に見た。例えば、\Phi(x,y) \mapsto (x,y,x^2+y^2) である。カーネル SVM を眺めてみる ではこの自作カーネルと多項式カーネル、RBF カーネルを用いて分類問題を解いたが特に結果に違いはなく旨みはまったく見えなかった。

ところが難しいデータセット、例えば Quantum feature maps and kernels における例として使われている ad_hoc_data を用いた場合には、RBF カーネルによる決定境界は健闘はしているものの以下のようになりあまり機能していない:

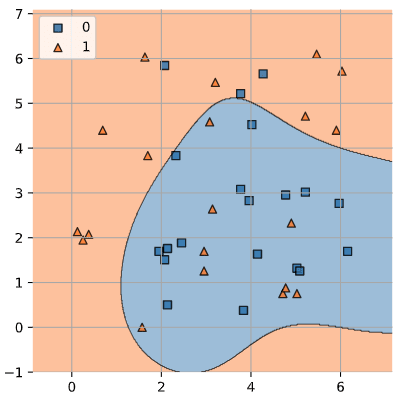
と、この ad_hoc_data という難しいデータセットは置いておいて、冒頭の同心円のデータセットに戻る。

カーネルを量子回路で定める

文献 [カーネル法] p.33 をみると

\begin{align*} \Phi:\ &\Omega &\!\!\to \quad&\mathcal{H} \\ &\xi &\!\!\mapsto \quad&\!\!\!k(\cdot, \xi) \end{align*}

をいう形で特徴写像がとられている。カーネルからの対応が一意かは分からないが、カーネルが複雑であれば、特徴写像もかなり複雑な関数であることが期待できそうな気はする。

ここでは、とても複雑なカーネルが構成できれば、それは古典的な多項式カーネルや RBF カーネルよりもきめの細かい特徴空間を扱うことになり、かなり複雑なデータセットでもクラス分類できる可能性がある くらいに考えておく。

以下、量子回路によるカーネル、いわゆる「量子カーネル」がそういうものになってくれると嬉しいという期待をこめる。

Supervised learning with quantum enhanced feature spaces

上記のようなことは、論文 [H-C-T-H-K-C-G] においては、

A necessary condition to obtain a quantum advantage, in either of the two approaches, is that the kernel cannot be estimated classically.

と表現されている。また、

For example, a classifier that uses a feature map that only generates product states can immediately be implement classically. To obtain an advantage over classical approaches we need to implement a map based on circuits that are hard to simulate classically.

ということで、古典的に近似できないようなカーネルの構成法として同論文で提案されているような量子回路が Qiskit では ZZFeatureMap として定義されており、例えば 2 量子ビットように繰り返し数 1 のマップとしては

from qiskit.circuit.library import ZZFeatureMap

ZZFeatureMap(feature_dimension=2, reps=1).decompose().draw()

のようにして使うことができる。

名前の由来としては、論文 [T-C-C-G] p.6 より e^{-i \theta Z \otimes Z} が量子回路としては以下のように実装されることからわかる[1]。これはいわゆる R_{zz} ゲート[2]と呼ばれるゲートで、R_{zz} をコンポーネントに用いた特徴マップなので、ZZFeatureMap なのである。

とにかくここでは、この R_{zz} を用いた量子回路が作るカーネルは古典的に近似が困難なものになると天下り的に思うことにする。

今回難しいことはする気はない。そんなに凄いカーネルなら当然、同心円のデータセットも綺麗にクラス分類できるよね？というのを見るにとどめる。

カーネルを作る

カーネル SVM を眺めてみる と同様に自作カーネルを作るのだが、今回は ZZFeatureMap を使った量子回路を用いて作成する。

ところで文献 [QSVM] では、opflow を使って自作カーネルを定義しているが、気がついたらいつの間にか定義が終わってしまい、狐に鼻をつままれたように感じるので、opflow を使わずに自分で実装する。

論文 [H-C-T-H-K-C-G] p.5 や pp.14-15 より、量子回路の部分を \mathcal{U}_{\Phi}(\xi) と書くことにすると、結局、n 量子ビットのケースでは

\begin{align*} k(\xi_j, \xi_i) = \left| \braket{0^n | \mathcal{U}_{\Phi}^\dagger(\xi_j) \mathcal{U}_{\Phi}(\xi_i) |0^n} \right|^2 \tag{2} \end{align*}

を (i,j)-成分に並べた行列が自作カーネル (k(\xi_i, \xi_j))_{1 \leq i,j \leq N} となる。今回は n=2 である。

ZZFeatureMap は PQC（パラメータ付き量子回路）なので、データセット x_data の内容を位相エンコーディングで回路のパラメータに取り込んでカーネルを計算する。

以下の実装でやっていることは、(2) 式の通りに

  • \mathcal{U}_{\Phi}(\xi_i) \ket{0^n} と \mathcal{U}_{\Phi}(\xi_j) \ket{0^n} を計算して
  • 内積をとって
  • 絶対値をとって
  • 2 乗する

というだけである。\mathcal{U}_{\Phi}(\xi_i) \ket{0^n} がどういう状態ベクトルになるかは測定して確率振幅を割り出すのが本来であるが、ここでは簡単のため状態ベクトルシミュレータを使って計算を行なっている。

from qiskit import QuantumCircuit
from qiskit_aer import AerSimulator

def calculate_kernel(zz_feature_map, x_data, y_data=None):
    if y_data is None:
        y_data = x_data
    sim = AerSimulator()
    x_matrix, y_matrix = [], []
    for x0, x1 in x_data:
        param0, param1 = zz_feature_map.parameters
        qc = zz_feature_map.bind_parameters({param0: x0, param1: x1})
        # .decompose() せずに .save_statevector() を使うとエラーになる。
        qc = qc.decompose()
        qc.save_statevector()
        sv = sim.run(qc).result().get_statevector()
        x_matrix.append(list(np.array(sv)))
    for y0, y1 in y_data:
        param0, param1 = zz_feature_map.parameters
        qc = zz_feature_map.bind_parameters({param0: y0, param1: y1})
        qc = qc.decompose()
        qc.save_statevector()
        sv = sim.run(qc).result().get_statevector()
        y_matrix.append(list(np.array(sv)))
    x_matrix, y_matrix = np.array(x_matrix), np.array(y_matrix)
    kernel = np.abs(
        y_matrix.conjugate() @ x_matrix.transpose()
    )**2
    return kernel

カーネルを計算して訓練する

冒頭のデータセット train_data を使って calculate_kernel で自作カーネルを計算して訓練する。

from sklearn.svm import SVC

zz_feature_map = ZZFeatureMap(feature_dimension=2, reps=2)
train_kernel = calculate_kernel(zz_feature_map, train_data)

model = SVC(kernel='precomputed')
model.fit(train_kernel, train_labels)

検証

テストカーネルも計算して、ラベルの推定結果を可視化する。

import matplotlib

test_kernel = calculate_kernel(zz_feature_map, train_data, test_data)
pred = model.predict(test_kernel)

fig = plt.figure(figsize=(5, 5))
ax = fig.add_subplot(111)
ax.set_aspect('equal')
ax.set_title("Predicted data classification")
ax.set_ylim(-2, 2)
ax.set_xlim(-2, 2)
for (x, y), pred_label in zip(test_data, pred):
    c = 'C0' if pred_label == 0 else 'C3'
    ax.add_patch(matplotlib.patches.Circle((x, y), radius=.01,
                 fill=True, linestyle='solid', linewidth=4.0,
                 color=c))
plt.grid()
plt.show()

大体良さそうな結果になった。念の為スコアも確認する。

model.score(test_kernel, test_labels)

1.0

まとめ

古典的なカーネル SVM と同様に自作カーネルを用いて量子カーネル SVM を行ってみた。とても簡単なデータセットで行ったのでまったく面白くない当たり前の結果になったが、それが狙いなので期待通りである。

再び論文 [H-C-T-H-K-C-G] に戻ると、Conclusions で

In the future it becomes intriguing to find suitable feature maps for this technique with provable quantum advantages while providing significant improvement on real world data sets.

と述べられている。つまり、量子カーネル SVM を使えばもの凄い分類精度になるとかそういう話ではなく、現実世界のある種の難しいデータセットであって、従来の古典的な手法ではアプローチが難しいようなものに対して、量子優位性が得られる特徴マップを量子回路で作れるといいよね、という話である。

とにかく、量子計算が絡んでくるのは類似度からなる自作カーネル（量子特徴マップを介したグラム行列）の計算部分だけで、他は古典的なカーネル SVM の話として理解できることがわかった。

次回の記事では、Blueqat を使って ZZFeatureMap さえも自作して掘り下げて（？）みたい。量子カーネル SVM で遊んでみる — Blueqat として公開予定である。

To be continued...

参考文献

脚注

  1. P ゲートと R_z ゲートはグローバル位相の差を除いて同一のゲートであった。 ↩︎

  2. RZZGate も参照。 ↩︎

GitHubで編集を提案

Discussion