Qiskit で遊んでみる (17) — Quantum Machine Learning その 3

目的

Qiskit で遊んでみる (15) — Quantum Machine Learning の内容を GPU シミュレーションで行いたい。そのために、今回は cuQuantum で遊んでみる (5) — VQE その 2 で触れた cuQuantum (cuTensorNet) を活用したい。

ナイーブな実装

Qiskit で遊んでみる (15) — Quantum Machine Learning での実装において、期待値計算を以下のようにすればいけるのだが、これがとてつもなく思い。期待計算と勾配計算のための QuantumCircuit をばらばらに構築するコストや、CircuitToEinsum のオーバーヘッド、そして小さいテンソル計算を GPU で行わせる非効率さのため、この訓練は EstimatorQNN で約 2 分程度だったところが、33min 31s かかってしまった。このため、これは採用しない。

    def _calc_expvals(self,
        qc_list: list[QuantumCircuit],
        qc_grad_list: list[QuantumCircuit],
        operator: str
    ) -> tuple[np.ndarray, np.ndarray]:
        qc_list_total = qc_list + qc_grad_list
        n_circuit = len(qc_list_total)

        expval_list = []
        for qc in qc_list_total:
            converter = CircuitToEinsum(qc)
            expr, operands = converter.expectation(hamiltonian)
            expval_list.append(cp.asnumpy(contract(expr, *operands).real))

        expval_array = np.array(expval_list)
        expvals = expval_array[:len(qc_list)]
        grad_list = expval_array[len(qc_list):].reshape(-1, 2)

        return expvals, grad_list

大きなテンソルを目指す

例えば、行列をベクトルに掛ける計算は、テンソルの縮約で書くと以下のようになる:

v = np.array([1,0])
A = np.arrah([[1,2], [3,4]])
print(np.einsum("a,ba->b", v, A))

[1 3]

これを複数のベクトルに対して一気に行いたいとしよう。すると、テンソルの階数を上げて以下のようにすれば良い:

vs = np.array([[1,0], [1, -2]])
A = np.arrah([[1,2], [3,4]])
print(np.einsum("ca,ba->cb", vs, A))

[[ 1 3]
[-3 -5]]

このことから、CircuitToEinsum で得られるテンソルにおいて、振幅エンコーディングに対応するテンソルの階数を上げて、データローダからのバッチをすべてスタックして詰め込めば良いことが想像できる。

量子回路とテンソルネットワーク

Iris データセットの Versicolor と Versinica とを分類する回路は以下のようなものにしていた:

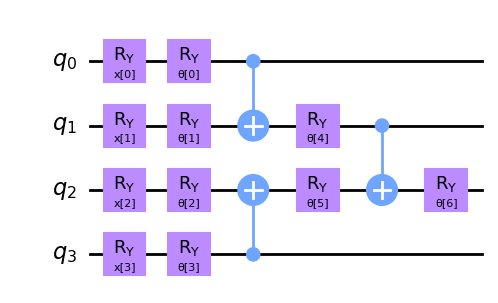
この回路が表現する状態ベクトルを $\ket{\psi(\theta)}$ とする時、ハミルトニアン $H$ の期待値は $\braket{\psi(\theta) | H | \psi(\theta)}$ で与えられる。このため、

converter = CircuitToEinsum(qc)
expr, operands = converter.expectation(hamiltonian)

は以下のようなテンソルネットワークを与える:

ノード 0, 1, 2, 3 は $\ket{0}$ に対応し、ノード 33, 34, 35, 36 は $\bra{0}$ に対応する。振幅エンコーディング $R_y(\theta)$ をしている側のノードは 4, 6, 10, 12 で、対応する出力側の $R_y^\dagger(\theta)$ は 24, 26, 30, 32 である。

この 8 つのテンソルは $R_y$ という行列に対応する 2 階のテンソルになっているが、ここにバッチ由来の振幅を全部突っ込んで、3 階のテンソルにする。

因みに、ノード 8, 14 が手前の $CX$ ゲートに対応する 4 階のテンソルであり、ノード 16 が奥の $CX$ で、ノード 18 がハミルトニアン $Z$ に対応する 2 階のテンソルである。読み方さえ覚えてしまえば、数学的な置換によって量子回路はテンソルネットワークに置き換えることができる。

分類器実装

準備

基本的には Qiskit で遊んでみる (15) — Quantum Machine Learning が流用されるため、差分を記載する。

ハミルトニアンについては、Qiskit では LSB が右であったが、cuTensorNet では LSB が左になるので以下のようになる:

hamiltonian = "IIZI"

続いて幾つかのユーティリティを用意する。勾配計算を楽に行うために、パラメータシフト則の実装に Python でリストの中身を一時的に置き換える で使ったテクニックを応用する:

# CuPy による Ry ゲートのテンソル表現を与える。
def Ry(theta):
    return cp.array([
        [cp.cos(theta/2), -cp.sin(theta/2)],
        [cp.sin(theta/2), cp.cos(theta/2)]
    ], dtype=complex)

# Qiskit の量子回路のパラメータ付き Ry ゲートの位置を特定する。
def find_ry_locs(
    qc_pl: QuantumCircuit,
    hamiltonian: str,
    return_tn: bool = False
) -> tuple[dict[str, tuple[int, int]], str, list[cp.ndarray]]:
    length = len(qc_pl.parameters)
    eps = 0.01
    params = np.arange(eps, np.pi, (np.pi-eps)/length)
    name2param = {pvec.name: p
                  for pvec, p in zip(qc_pl.parameters, params)}
    qc = qc_pl.bind_parameters(params)
    converter = CircuitToEinsum(qc)
    expr, operands = converter.expectation(hamiltonian)

    pname2locs = {}
    for name, p in name2param.items():
        ry = Ry(p)
        ry_dag = Ry(-p)
        loc = None
        dag_loc = None
        for i, t in enumerate(operands):
            if cp.allclose(t, ry):
                loc = i
            elif cp.allclose(t, ry_dag):
                dag_loc = i  # i - len(operands)
            if loc and dag_loc:
                pname2locs[name] = [loc, dag_loc]
                break
    if return_tn:
        return pname2locs, expr, operands
    else:
        return pname2locs

# 振幅エンコーディングを行う Ry ゲート部分にバッチ由来のテンソルを埋め込む。
# バッチなので、縮約記号を撥 (バチ) にした。
def replace_by_batch(
    expr: str,
    operands: list[cp.ndarray],
    pname2theta_list: dict[str, list[float] | np.ndarray],
    pname2locs: dict[str, tuple[int, int]]
) -> list[cp.ndarray]:
    batch_symbol = "撥"  # symbols are: a, b, c, ..., z, A, B, C, ..., 撥
    ins, out = re.split(r"\s*->\s*", expr)
    ins = re.split(r"\s*,\s*", ins)
    for pname, theta_list in pname2theta_list.items():  # e.g. pname[0] = "x[0]"
        batch = cp.array([Ry(theta) for theta in theta_list])
        batch_dag = cp.array([Ry(-theta) for theta in theta_list])
        loc, dag_loc = pname2locs[pname]
        operands[loc] = batch
        operands[dag_loc] = batch_dag
        if len(ins[loc]) == 2:
            ins[loc] = batch_symbol + ins[loc]
        if len(ins[dag_loc]) == 2:
            ins[dag_loc] = batch_symbol + ins[dag_loc]
    if len(out) == 0:
        out = batch_symbol
    new_expr = ",".join(ins) + "->" + out

    return new_expr, operands

# ansatz のパラメータを設定する。
def replace_ry(
    operands: list[cp.ndarray],
    pname2theta: dict[str, float],
    pname2locs: dict[str, tuple[int, int]]
) -> list[cp.ndarray]:
    for pname, theta in pname2theta.items():  # e.g. pname[0] = "θ[0]"
        ry = Ry(theta)
        ry_dag = Ry(-theta)
        loc, dag_loc = pname2locs[pname]
        operands[loc] = ry
        operands[dag_loc] = ry_dag

    return operands

# ansatz のパラメータを一時的に上書きする。勾配計算のパラメータシフト則で利用する。
@contextlib.contextmanager
def temporarily_replace_ry(
    operands: list[cp.ndarray],
    pname: str,
    pname2theta: dict[str, float],
    pname2locs: dict[str, tuple[int, int]],
    phase_shift: float = np.pi / 2
):
    backups = {}
    try:
        theta = pname2theta[pname]  # e.g. pname = "θ[0]"
        loc, dag_loc = pname2locs[pname]
        backups = {
            loc: operands[loc],
            dag_loc: operands[dag_loc]
        }
        operands[loc] = Ry(theta + phase_shift)
        operands[dag_loc] = Ry(-(theta + phase_shift))
        yield operands
    finally:
        for i, v in backups.items():
            operands[i] = v

分類器

Qiskit の Estimator のマナーにインスパイアされたような実装を行う:

class PQCTrainerTN:
    def __init__(self,
        qc: QuantumCircuit,
        initial_point: Sequence[float],
        optimizer: optimizers.Optimizer
    ):
        self.qc_pl = qc  # placeholder circuit
        self.initial_point = np.array(initial_point)
        self.optimizer = optimizer

    def fit(self,
        dataset: Dataset,
        batch_size: int,
        operator: str,
        callbacks: list | None = None,
        epochs: int = 1
    ):
        pname2locs, expr, oprands = find_ry_locs(
            self.qc_pl, operator, return_tn=True
        )

        dataloader = DataLoader(dataset, batch_size, shuffle=True, drop_last=True)
        callbacks = callbacks if callbacks is not None else []

        opt_loss = sys.maxsize
        opt_params = None
        params = self.initial_point.copy()
        if isinstance(params, list):
            params = np.array(params)

        for epoch in range(epochs):
            for batch, label in dataloader:
                batch, label = self._preprocess_batch(batch, label)
                label = label.reshape(label.shape[0], -1)

                pname2theta = {f"θ[{i}]": params[i] for i in range(len(params))}
                expr, oprands = self._prepare_circuit(
                    batch, pname2theta, pname2locs, expr, oprands
                )

                # "forward"
                expvals = self._forward(expr, oprands)
                total_loss = np.mean((expvals - label)**2)

                # "backward"
                grads = self._backward(expr, oprands, pname2theta, pname2locs)
                expvals_minus_label = (expvals - label).reshape(batch.shape[0], -1)
                # コスト関数の勾配を組み立てて、バッチでの平均をとる。
                total_grads = np.mean(expvals_minus_label * grads, axis=0)

                if total_loss < opt_loss:
                    opt_params = params.copy()
                    opt_loss = total_loss

                    with open("opt_params_iris_tn.pkl", "wb") as fout:
                        pickle.dump(opt_params, fout)

                # "update params"
                self.optimizer.update(params, total_grads)

                for callback in callbacks:
                    callback(total_loss, params)

        return opt_params

    def _preprocess_batch(self,
        batch: torch.Tensor,
        label: torch.Tensor
    ) -> tuple[np.ndarray, np.ndarray]:
        batch = batch.detach().numpy()
        label = label.detach().numpy()
        return batch, label

    def _prepare_circuit(self,
        batch: np.ndarray,
        pname2theta: dict[str, float],
        pname2locs: tuple[dict[str, tuple[int, int]]],
        expr: str,
        operands: list[cp.ndarray]
    ) -> tuple[str, list[cp.ndarray]]:
        pname2theta_list = {f"x[{i}]": batch[:, i].flatten().tolist()
                            for i in range(batch.shape[1])}
        # 振幅エンコーディングでバッチを詰め込む。
        expr, operands = replace_by_batch(
            expr, operands, pname2theta_list, pname2locs
        )

        # ansatz のパラメータをセットする。
        operands = replace_ry(
            operands, pname2theta, pname2locs
        )

        return expr, operands

    def _forward(self,
        expr: str,
        operands: list[cp.ndarray]
    ) -> np.ndarray:
        return cp.asnumpy(contract(expr, *operands).real.reshape(-1, 1))

    def _backward(self,
        expr: str,
        operands: list[cp.ndarray],
        pname2theta: dict[str, float],
        pname2locs: dict[str, tuple[int, int]]
    ) -> np.ndarray:
        expval_array = []
        for i in range(len(pname2theta)):
            pname = f"θ[{i}]"
            # パラメータシフト則で勾配計算を行う。
            with temporarily_replace_ry(
                operands, pname, pname2theta, pname2locs, np.pi/2
            ):
                expvals_p = cp.asnumpy(contract(expr, *operands).real.flatten())
            with temporarily_replace_ry(
                operands, pname, pname2theta, pname2locs, -np.pi/2
            ):
                expvals_m = cp.asnumpy(contract(expr, *operands).real.flatten())
            expvals = ((expvals_p - expvals_m) / 2)
            expval_array.append(expvals)

        # batch grads_i is converted to a column vector
        return np.array(expval_array).T

訓練ループ

def RunPQCTrain(
    dataset: Dataset,
    batch_size: int,
    qc: QuantumCircuit,
    operator: str,
    init: Sequence[float] | None = None,
    epochs: int = 1,
    interval: int = 100
):
    # Store intermediate results
    history = {"loss": [], "params": []}
    cnt = 0

    def store_intermediate_result(loss, params):
        nonlocal cnt
        if cnt % interval != 0:
            return
        history["loss"].append(loss)
        history["params"].append(None)
        print(f'{loss=}')

    optimizer = optimizers.Adam(alpha=0.01)
    trainer = PQCTrainerTN(qc=qc, initial_point=init, optimizer=optimizer)
    result = trainer.fit(
        dataset, batch_size, operator,
        callbacks=[store_intermediate_result], epochs=epochs
    )

    return result, history["loss"]

メインの実装はここまでである。

実験を行う

%%time

length = make_ansatz(n_qubits, dry_run=True)
placeholder_circuit = make_placeholder_circuit(n_qubits)

np.random.seed(10)
init = np.random.random(length) * 2*math.pi

opt_params, loss_list = RunPQCTrain(trainset, 32,
                                    placeholder_circuit, hamiltonian, init=init,
                                    epochs=100, interval=500)

print(f'final loss={loss_list[-1]}')
print(f'{opt_params=}')

ナイーブな実装では 33min 31s かかったが、今回の実装で、凡そ 2 分まで短縮された。早い時は 1min 27s 程度で完了した。Google Colab 上で実行すると 2 分を切りやすいように感じた。

テスト精度

testloader = DataLoader(testset, 32)

qc_pl = make_placeholder_circuit(n_qubits)
pname2locs, expr, operands = find_ry_locs(qc_pl, hamiltonian, return_tn=True)
pname2theta = {f"θ[{i}]": params[i] for i in range(len(params))}

total = 0
total_correct = 0

for i, (batch, label) in enumerate(testloader):
    batch, label = batch.detach().numpy(), label.detach().numpy()

    pname2theta_list = {f"x[{i}]": batch[:, i].flatten().tolist()
                        for i in range(batch.shape[1])}
    expr, operands = replace_by_batch(
        expr, operands, pname2theta_list, pname2locs
    )

    operands = replace_ry(
        operands, pname2theta, pname2locs
    )

    expvals = cp.asnumpy(contract(expr, *operands).real)

    predict_labels = np.ones_like(expvals)
    predict_labels[np.where(expvals < 0)] = -1
    predict_labels = predict_labels.astype(int)

    total_correct += np.sum(predict_labels == label)
    total += batch.shape[0]

print(f'test acc={np.round(total_correct/total, 2)}')

test acc=0.9

データセットが小さいこともあり、実行ごとに多少最適化後のパラメータに差が出るのか、test acc は 0.83, 0.87, 0.9 あたりが出やすかった。1 回だけ 0.96 というのも見たが、再現できていない。ガチャみたいな感じである。

まとめ

4 量子ビット程度の量子回路での QML において、CPU 版と大差ない速度で実験可能なテンソルネットワーク計算を行った。

EstimatorQNN の場合、内部的に状態ベクトル計算を行っているので、量子ビット数 $n$ に対してメモリの消費量料が $\mathcal{O}(2^n)$ でスケールする。Qiskit Aer のシミュレータでサンプリングベースで期待値計算を行えばより少ない消費メモリで済みそうであるが、shots = 10000 くらいで行わないとなかなか正確な期待値は計算できないように見えた。

今回の手法では、量子計算的な部分を全部捨て去って、ただのテンソル計算にしてしまっているが、高速かつ、大量の量子ビット数へのスケール性能が期待される。量子ビット数に応じて生じる理論的な Barren Plateau の有無や挙動を調査するのに役立つかもしれない。