Qiskit で遊んでみる (15) — Quantum Machine Learning
目的
Edward Grant et al. の Hierarchical quantum classifiers (arXiv:1804.03680) という論文があって、面白そうなので実装して試してみようという内容。
今回はその中の予備実験にあたる? Iris データセットでの Tree TensorNetwork Classifier を試す[1]。
概要
少々読み違えているところもあるかもしれないが、以下の設定とした。
- Iris データセット (4 次元)、或は MNIST (784 次元) を量子回路に振幅エンコーディングする。MNIST の場合は次元が大きいので、主成分分析 (PCA) を用いて 8 次元に落とす。
- 量子回路は TTN (Tree TensorNetwork) か MERA (Multi-scale entanglement renormalization) の構造を用いる。
- ハミルトニアン
I \otimes \cdots I \otimes Z \otimes I \otimes \cdots I \{-1, 1\} - 勾配を推定し、Adam オプティマイザでパラメータを最適化する確率的勾配降下アルゴリズムを用いる。
具体的な回路の構造は、MNIST については Figure 1 を、Iris については Figure 6 を見れば良い。
実験環境
$ pip list | grep qiskit
qiskit 0.44.0
qiskit-aer-gpu-cu11 0.12.2
qiskit-dynamics 0.4.1
qiskit-experiments 0.5.3
qiskit-finance 0.3.4
qiskit-ibm-experiment 0.2.7
qiskit-ibmq-provider 0.20.2
qiskit-machine-learning 0.6.1
qiskit-nature 0.6.2
qiskit-optimization 0.5.0
qiskit-terra 0.25.0
$ pip list | grep torch
torch 2.0.1+cu118
torchaudio 2.0.2+cu118
torchmetrics 0.11.1
torchvision 0.15.2+cu118
準備
必要なコンポーネントを用意していく。特に QML に利用できる Adam オプティマイザとデータローダを調達する。
オプティマイザ
1 つの候補は numpy-ml で、Python 3.9 までは AS IS で利用できるが、Python 3.10 では 1 箇所修正しないとならない。もう 1 つの候補は dezero で、これは本来は「ゼロから作るDeep Learning ❸」で作成するフレームワーク「DeZero」である。
今回は後者を採用した。Adam だけ欲しいので局所的に切り出せるためである。コードは MIT ライセンスで提供されており非常に使いやすい。deep-learning-from-scratch-3/dezero/optimizers.py を改造して以下のようにした:
from __future__ import annotations
import math
import numpy as np
# =============================================================================
# Optimizer (base class)
# =============================================================================
class Optimizer:
def __init__(self):
self.hooks = []
def update(self, params, grads) -> None:
for f in self.hooks:
f(params)
self.update_one(params, grads)
def update_one(self, params, grads) -> None:
raise NotImplementedError()
def add_hook(self, f):
self.hooks.append(f)
# =============================================================================
# SGD / MomentumSGD / AdaGrad / AdaDelta / Adam
# =============================================================================
class Adam(Optimizer):
def __init__(self, alpha=0.001, beta1=0.9, beta2=0.999, eps=1e-8):
super().__init__()
self.t = 0
self.alpha = alpha
self.beta1 = beta1
self.beta2 = beta2
self.eps = eps
self.ms = {}
self.vs = {}
def update(self, *args, **kwargs):
self.t += 1
super().update(*args, **kwargs)
@property
def lr(self):
fix1 = 1. - math.pow(self.beta1, self.t)
fix2 = 1. - math.pow(self.beta2, self.t)
return self.alpha * math.sqrt(fix2) / fix1
def update_one(self, params, grads):
key = 'Adam'
if key not in self.ms:
self.ms[key] = self.np.zeros_like(params)
self.vs[key] = self.np.zeros_like(params)
m, v = self.ms[key], self.vs[key]
beta1, beta2, eps = self.beta1, self.beta2, self.eps
grad = grads
m += (1 - beta1) * (grad - m)
v += (1 - beta2) * (grad * grad - v)
params -= self.lr * m / (self.np.sqrt(v) + eps)
データセットとデータローダ
Iris だけならどういう実装でも良いのだが、色んなデータセットを扱う場合、Torchvision は便利である。となれば、データローダとして PyTorch のものに乗せると後々楽ができそうである。ということで以下のような仕組みを用意する。テンソルの変換を適用できるような TersorDataset が欲しいという内容について、フォーラム Transforms for TensorDataset() に良い答えが書かれていたのでこれも参考にした。
class SimpleToTensor:
def __init__(self, dtype=int):
self.dtype=dtype
def __call__(self, x):
return torch.tensor(x, dtype=self.dtype)
def __repr__(self) -> str:
return f"{self.__class__.__name__}()"
def transform_label(label):
return 1 if label == 1 else -1
target_transform = transforms.Compose([
SimpleToTensor(),
transform_label
])
class TransformableDataset(Dataset):
def __init__(self,data, target, transform=None, target_transform=None):
self.data = data
self.target = target
self.transform = transform
self.target_transform = target_transform
def __len__(self):
return len(self.data)
def __getitem__(self, index):
x = self.data[index]
if self.transform:
x = self.transform(x)
y = self.target[index]
if self.target_transform:
y = self.target_transform(y)
return x, y
transform_label の内容は暗黙のうちに、Versicolor とその他での二値分類を想定している。Setosa (0), Versicolor (1), Versinica (2) で、特に今回は Versicolor (1) vs Versinica (2) をするので、Versinica を -1 になるようにしている。データローダは PyTorch のものを AS IS で使うことにする。
メイン実装
準備ができたのでメインの実装を進める。基本的には深層学習のそれと同じである。
基本的には論文の通りに実装するので、Qiskit の言葉に翻訳する程度である。
必要なモジュールを import する
from __future__ import annotations
import os
import sys
import math
import pickle
from collections.abc import Sequence
from sklearn import datasets
from sklearn.model_selection import train_test_split
import torch
from torch.utils.data import DataLoader, Dataset, TensorDataset
import torchvision
import torchvision.transforms as transforms
import numpy as np
import matplotlib.pyplot as plt
sys.path.append('.')
import common.optimizers as optimizers
from qiskit import QuantumCircuit
from qiskit.circuit import ParameterVector
from qiskit.quantum_info import SparsePauliOp
from qiskit.primitives import BaseEstimator, Estimator
from qiskit.quantum_info.operators.base_operator import BaseOperator
from qiskit_machine_learning.neural_networks import EstimatorQNN
Versicolor と Versinica のみのデータセットを作る
iris = datasets.load_iris()
# Sersicolor (1) と Versinica (2)
indices = np.where((iris.target==1) | (iris.target==2))
versicolor_versinica_data = np.squeeze(iris.data[indices, :], axis=0)
versicolor_versinica_target = iris.target[indices]
X_train, X_test, y_train, y_test = train_test_split(
versicolor_versinica_data, versicolor_versinica_target,
test_size=0.3, random_state=1234
)
trainset = TransformableDataset(
X_train, y_train, SimpleToTensor(float), target_transform
)
testset = TransformableDataset(
X_test, y_test, SimpleToTensor(float), target_transform
)
量子分類器を実装する
論文の Figure 1, 2, 6 に注意して実装する。
n_qubits = 4
# Eqn. (1)
def make_init_circuit(
n_qubits: int,
dry_run: bool = False
) -> QuantumCircuit | int:
if dry_run:
return n_qubits
init_circuit = QuantumCircuit(n_qubits)
x = ParameterVector('x', n_qubits)
for i in range(n_qubits):
init_circuit.ry(x[i], i)
return init_circuit
# Fig. 1 (a) TTN classifier
def make_ansatz(
n_qubits: int,
insert_barrier: bool = False,
dry_run: bool = False
) -> QuantumCircuit | int:
def append_U(qc, i, j, thetas, count, last_unitary=False, reverse=False):
qc.ry(thetas[count], i)
count += 1
qc.ry(thetas[count], j)
count += 1
if reverse:
ansatz.cx(j, i)
else:
ansatz.cx(i, j)
if last_unitary:
qc.ry(thetas[count], j)
count += 1
return count
length = 2*n_qubits//2 # U5 - U6
length += 3*n_qubits//4 # U7
if dry_run:
return length
thetas = ParameterVector('θ', length)
count = 0
ansatz = QuantumCircuit(n_qubits)
# U5 - U6
reverse = False
for i in range(0, n_qubits, 2):
if i+1 >= n_qubits:
break
count = append_U(ansatz, i, i+1, thetas, count, reverse=reverse)
reverse = not reverse
if insert_barrier:
ansatz.barrier()
# U7
for i in range(1, n_qubits, 4):
if i+1 >= n_qubits:
break
count = append_U(ansatz, i, i+1, thetas, count, last_unitary=True)
if insert_barrier:
ansatz.barrier()
assert count == length, count
return ansatz
def make_placeholder_circuit(
n_qubits: int,
insert_barrier: bool = False,
dry_run: bool = False
) -> QuantumCircuit | int:
if dry_run:
length_feature = make_init_circuit(n_qubits, dry_run=True)
length_ansatz = make_ansatz(n_qubits, dry_run=True)
length = length_feature + length_ansatz
return length
qc = make_init_circuit(n_qubits)
ansatz = make_ansatz(n_qubits, insert_barrier)
qc.compose(ansatz, inplace=True)
return qc
placeholder_circuit = make_placeholder_circuit(n_qubits)
display(placeholder_circuit.draw())
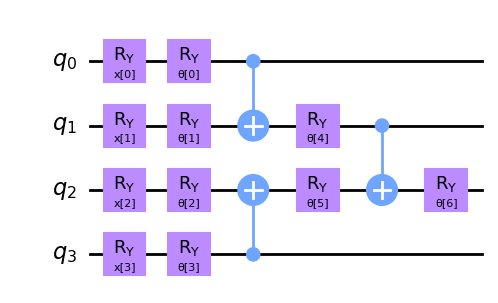
期待値を推定するハミルトニアンを定義する
ハミルトニアンが論文には具体的には書いていないが、観測量
hamiltonian = SparsePauliOp('IZII') # 3rd position from the right, c.f. Fig. 1
訓練ループを実装する
基本的に PyTorch みたいな感じになる。EstimatorQNN の説明
- gradient (BaseEstimatorGradient | None) – The estimator gradient to be used for the backward pass. If None, a default instance of the estimator gradient, ParamShiftEstimatorGradient, will be used.
にあるように、特に指定しなければ勾配計算はパラメータシフト則が使われる。
なお、def _backward の内容より、コスト関数としての勾配計算ではなく、
class PQCTrainerEstimatorQnn:
def __init__(self,
qc: QuantumCircuit,
initial_point: Sequence[float],
optimizer: optimizers.Optimizer,
estimator: BaseEstimator | None = None
):
self.qc_pl = qc # placeholder circuit
self.initial_point = np.array(initial_point)
self.optimizer = optimizer
self.estimator = estimator
def fit(self,
dataset: Dataset,
batch_size: int,
operator: BaseOperator,
callbacks: list | None = None,
epochs: int = 1
):
dataloader = DataLoader(dataset, batch_size, shuffle=True, drop_last=True)
callbacks = callbacks if callbacks is not None else []
opt_loss = sys.maxsize
opt_params = None
params = self.initial_point.copy()
n_qubits = self.qc_pl.num_qubits
qnn = EstimatorQNN(
circuit=self.qc_pl, estimator=self.estimator, observables=operator,
input_params=self.qc_pl.parameters[:n_qubits],
weight_params=self.qc_pl.parameters[n_qubits:]
)
print(f'num_inputs={qnn.num_inputs}')
for epoch in range(epochs):
for batch, label in dataloader:
batch, label = self._preprocess_batch(batch, label)
label = label.reshape(label.shape[0], -1)
expvals = qnn.forward(input_data=batch, weights=params)
total_loss = np.mean((expvals - label)**2)
_, grads = qnn.backward(input_data=batch, weights=params)
grads = np.squeeze(grads, axis=1)
# コスト関数の勾配を組み立てて、バッチでの平均をとる。
total_grads = np.mean((expvals - label) * grads, axis=0)
if total_loss < opt_loss:
opt_params = params.copy()
opt_loss = total_loss
with open('opt_params_iris.pkl', 'wb') as fout:
pickle.dump(opt_params, fout)
self.optimizer.update(params, total_grads)
for callback in callbacks:
callback(total_loss, params)
return opt_params
def _preprocess_batch(self,
batch: torch.Tensor,
label: torch.Tensor
) -> tuple[np.ndarray, np.ndarray]:
batch = batch.detach().numpy()
label = label.detach().numpy()
return batch, label
def RunPQCTrain(
dataset: Dataset,
batch_size: int,
qc: QuantumCircuit,
operator: BaseOperator,
init: Sequence[float] | None = None,
estimator: Estimator | None = None,
epochs: int = 1,
interval = 100
):
# Store intermediate results
history = {'loss': [], 'params': []}
cnt = 0
def store_intermediate_result(loss, params):
nonlocal cnt
if cnt % interval != 0:
return
history['loss'].append(loss)
history['params'].append(None) # とりあえず保存しないことにする。
print(f'{loss=}')
# alpha の値はデフォルトより大きいほうが収束が早かった。
optimizer = optimizers.Adam(alpha=0.01)
trainer = PQCTrainerEstimatorQnn(
estimator=estimator, qc=qc, initial_point=init, optimizer=optimizer
)
result = trainer.fit(
dataset, batch_size, operator,
callbacks=[store_intermediate_result], epochs=epochs
)
return result, history['loss']
実装はここまでである。
実験を行う
バッチサイズ 32 で 100 エポック回す。500 回のパラメータ更新ごとにコスト値を出す。
length = make_ansatz(n_qubits, dry_run=True)
placeholder_circuit = make_placeholder_circuit(n_qubits)
np.random.seed(10)
init = np.random.random(length) * 2*math.pi
estimator = Estimator()
opt_params, loss_list = RunPQCTrain(
trainset, 32,
placeholder_circuit, hamiltonian, init=init, estimator=estimator,
epochs=100, interval=500)
print(f'final loss={loss_list[-1]}')
print(f'{opt_params=}')
結果を検証する
コスト値のプロット
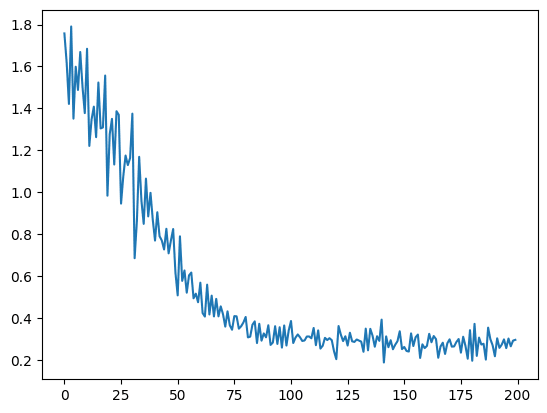
コストの変化をプロットすると以下のように徐々に下がっていくことが分かる。ある程度以上は下がらないので、ネットワークのパラメータ数が少ないのかもしれない。
plt.plot(range(len(loss_list)), loss_list)
plt.show()
テスト精度
ネットワークの出力は [-1, 1] の範囲なので、0 以上を 1、0 未満を -1 のラベルに対応付けて、正解ラベルと比較する。
testloader = DataLoader(testset, 32)
qc_pl = make_placeholder_circuit(n_qubits)
estimator = Estimator()
total = 0
total_correct = 0
for i, (batch, label) in enumerate(testloader):
batch, label = batch.detach().numpy(), label.detach().numpy()
qc_list = []
for i in range(batch.shape[0]):
data = batch[i, :]
qc_placeholder = qc_pl.copy()
qc = qc_placeholder.bind_parameters(data.tolist() + params.tolist())
qc_list.append(qc)
job = estimator.run(qc_list, [hamiltonian]*len(qc_list))
result = job.result()
expvals = result.values
predict_labels = np.ones_like(expvals)
predict_labels[np.where(expvals < 0)] = -1
predict_labels = predict_labels.astype(int)
total_correct += np.sum(predict_labels == label)
total += batch.shape[0]
print(f'test acc={np.round(total_correct/total, 2)}')
0.9
何度か試したが、30 個のテストデータのうち、27 個程度が正しく分類され、分類精度は 90% 程度となった。実行時間は最近の PC で約 2 分程度と短く、ちょっと手直しして再実験することも気楽にできる。
Appendix: パラメータシフト則とコスト関数の勾配
最後に勾配の計算について見ておこう。Maria Schuld et al. の Evaluating analytic gradients on quantum hardware や後続の論文によると、パラメータ付きの Pauli 回転ゲートからなる PQC (または ansatz)
で与えられる。
よって、今回のような
で与えられる。
まとめ
既に Quantum Neural Networks から始まる一連のチュートリアルが存在する。但し、事例が少なく他のデータセットに適用したい場合がやや不透明で、また、最適化を SDK に任せるのでその下がどうなっているのか分かりにくい部分もあると感じる。
そのような背景があって、自分でも理解を深めるために訓練ループも実装する形で実装を行った。なお、パラメータシフト則は上記の通りにシンプルな実装で済むので自前実装を行い、EstimatorQNN の代わりに Estimator を使っても同様の結果を得られる。但し、それは EstimatorQNN を再発明するようなものなので、実装が長くなり見通しが悪くなる。よって、今回は素直に EstimatorQNN を用いた。
-
既に MNIST のほうも試しているが、内容的に同様にやればちゃんと結果が出る。 ↩︎
Discussion