👏

Pythonで接線ポートフォリオを計算する

2023/12/23に公開

Python

ポートフォリオ

株価

tech

はじめに

前回の記事で、ポートフォリオを最適化して効率的フロンティアを書きました。今回は、無リスク資産を導入して、接線ポートフォリオを計算します。

無リスク資産

無リスク資産とは、先進国の短期国債のようにリスクなく投資ができる資産のことです^[1]。この記事では無リスク資産の年間の利益率を $r_f$ とします。

シャープ・レシオ

リスクがある資産のポートフォリオに対して、効率性の基準を考えます。ポートフォリオを選択する場合、リスクを取るほどリターンが大きくなることが期待されます。そのため、それぞれのポートフォリオが、無リスク資産という基準からどれだけリスクを取って、代わりにリターンを獲得したのかの基準を考えることができます。

このように考えたポートフォリオの基準はシャープ・レシオと呼ばれ、以下の式で表されます。

S_p = \frac{\mu_p - r_f}{\sigma_p}

ここで、 $\mu_p$ はポートフォリオの期待収益率、 $\sigma_p$ はポートフォリオの標準偏差です。

シャープ・レシオはポートフォリオの期待収益率が大きく標準偏差が小さいほど大きくなリます。リスクが小さく大きな収益を得られるポートフォリオが良いとされるため、シャープ・レシオが大きいポートフォリオが良いとされます。

接点ポートフォリオ

全てのポートフォリオの中で、シャープ・レシオが最大になるポートフォリオ計算します。

はじめに、前回と同様に、幾何ブラウン運動に基づいて株価をシミュレーションします。

ソースコード

import scipy.optimize as sco
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

np.random.seed(777)


def GBM(mu, sigma, S0, dt, T):
    """
    simulates a geometric Brownian motion

    Parameters
    ----------
    mu : float
        expected return
    sigma : float
        volatility
    S0 : float
        initial stock price
    dt : float
        time increment
    T : float
        final time
    """
    # number of time increments
    N = int(T / dt)

    # time vector
    t = np.linspace(0, T, N + 1)

    # Brownian increments
    W = np.cumsum(np.random.standard_normal(N + 1)) * np.sqrt(dt)

    # geometric Brownian motion
    S = S0 * np.exp((mu - 0.5 * sigma**2) * t + sigma * W)

    # return the time and stock price paths as a tuple
    df = pd.DataFrame({"time": t, "price": S})
    return df


mu = 0.01
sigma = 0.03
dt = 1 / (252)

assets = [
    {
        "name": "asset" + str(i),
        "param": {
            "mu": mu * i,
            "sigma": sigma * i,
            "S0": 100,
            "dt": dt,
            "T": 30,
        },
    }
    for i in range(1, 11)
]


df = pd.DataFrame()
for asset in assets:
    df[asset["name"]] = GBM(**asset["param"])["price"]

df.plot(figsize=(15, 8))

次に、ポートフォリオの収益率と標準偏差を計算します。

ソースコード

def calulate_summary(returns):
    risk = returns.std() * np.sqrt(1 / dt)
    log_returns = np.log(returns + 1)
    cagr = np.exp(log_returns.mean() / dt) - 1
    summary = pd.DataFrame({"CAGR": cagr, "Risk": risk})
    return summary


returns = df.pct_change().dropna()
summary = calulate_summary(returns)

cov_matrix = returns.cov() / dt
risk_free_rate = 0.01

	CAGR	Risk
asset1	0.017008	0.030107
asset2	0.029379	0.060334
asset3	0.034567	0.089926
asset4	0.014631	0.120006
asset5	0.028171	0.150103
asset6	0.037967	0.179590
asset7	0.049239	0.210934
asset8	0.014132	0.240883
asset9	0.044923	0.271013
asset10	0.028657	0.302420

次に、効率的フロンティアを計算します。

ソースコード

def portfolio_return(weights):
    cagr = summary["CAGR"].dot(weights)
    return cagr


def portfolio_volatility(weights):
    risk = np.sqrt(weights.dot(cov_matrix).dot(weights))
    return risk

# efficient frontier

equal_weights = np.ones(len(assets)) / len(assets)
target_cagrs = np.linspace(summary["CAGR"].min(), summary["CAGR"].max(), 100)
bnds = tuple((0, 1) for asset in assets)

volatilites = []
for target_cagr in target_cagrs:
    constraints = (
        {"type": "eq", "fun": lambda x: portfolio_return(x) - target_cagr},
        {"type": "eq", "fun": lambda x: x.sum() - 1},
    )
    result = sco.minimize(
        portfolio_volatility,
        equal_weights,
        method="SLSQP",
        bounds=bnds,
        constraints=constraints,
    )
    volatilites.append(result["fun"])

次に、全てのポートフォリオから、シャープ・レシオが最大のポートフォリオを計算します。

ソースコード


def portfolio_shape(weights):
    risk = portfolio_volatility(weights)
    cagr = portfolio_return(weights)
    return -(cagr - risk_free_rate) / risk

# Market portfolio

constraints = {"type": "eq", "fun": lambda x: x.sum() - 1}
opts = sco.minimize(
    portfolio_shape, equal_weights, method="SLSQP", bounds=bnds, constraints=constraints
)
market_weights = opts["x"]

market_cagr = portfolio_return(market_weights)
market_risk = portfolio_volatility(market_weights)
market_shape = -portfolio_shape(market_weights)

summary.loc["market portfolio"] = [market_cagr, market_risk]

シャープ・レシオの定義より、シャープ・レシオが最大のポートフォリオは、無リスク資産から効率的フロンティアに接線を引いたときの接点になります^[2]。そのため、シャープ・レシオが最大のポートフォリオは接線ポートフォリオと呼ばれます。

最後に、効率的フロンティアと接点ポートフォリオを可視化します。

ソースコード

plt.figure(figsize=(15, 8))

plt.scatter(summary["Risk"], summary["CAGR"])
for i in summary.index:
    plt.annotate(i, (summary["Risk"][i], summary["CAGR"][i]))

plt.plot(np.array([0, 0.06]), risk_free_rate + np.array([0, 0.06]) * market_shape)
plt.plot(volatilites, target_cagrs)
plt.xlabel("Risk")
plt.ylabel("CAGR")
plt.show()

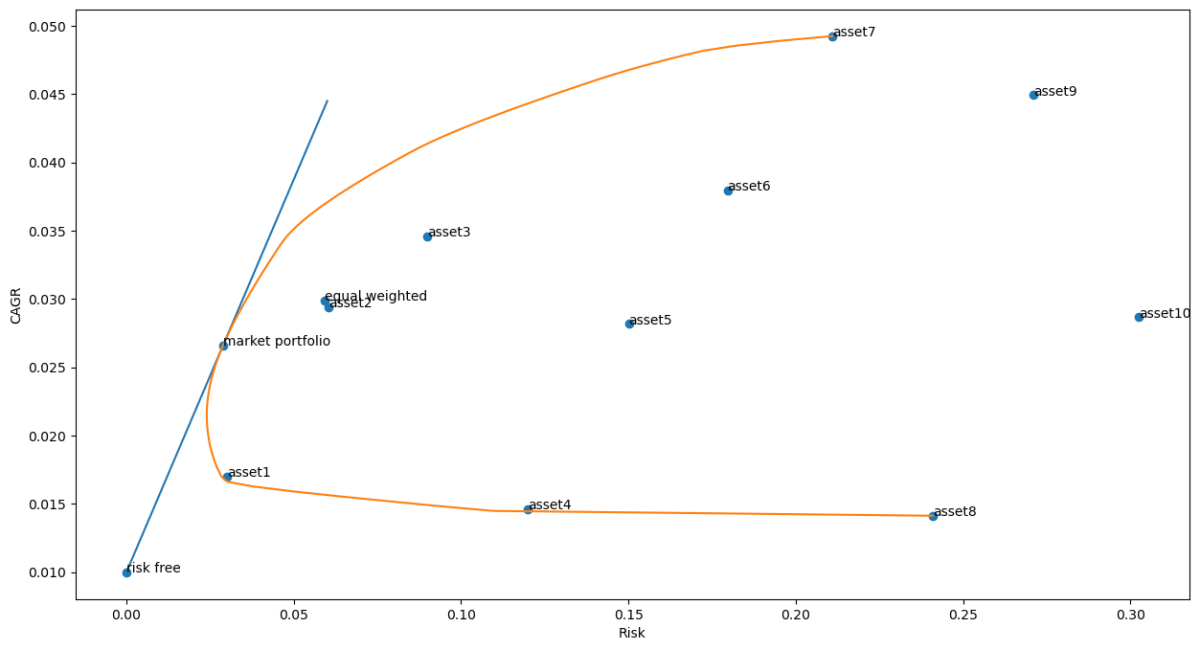
マーケットポートフォリオ

さらに、接点ポートフォリオの価格変化は次のようになります。

マーケット価格

非常に安定した成長をしていることがわかります。

まとめ

シャープ・レシオが最大のポートフォリオを計算しました。また、無リスク資産から効率的フロンティアに接線を引き可視化を行いました。

脚注

はじめに

無リスク資産

シャープ・レシオ

接点ポートフォリオ

まとめ

Discussion