Zenn
🐡

Pythonで株価のポートフォリオを最適化して効率的フロンティアを描く

2023/12/16に公開
Python
#
ポートフォリオ
#
株価
tech

はじめに

Pythonで株価のポートフォリオを最適化して効率的フロンティアを描く方法を紹介します。

株価のシミュレーション

この記事では、株価が幾何ブラウン運動に従うと仮定します。この仮定のもとで株価の確率変数は以下のようになります。[1]

S = S_0 \exp \left( \left( \mu - \frac{\sigma^2}{2} \right) t + \sigma W_t \right)

ここで、S_0は初期株価、\muは平均収益率、\sigmaはボラティリティ、W_tはブラウン運動の確率変数です。また、ブラウン運動の確率変数W_tは、正規分布N(0, t)に従います。

これをPythonでシミュレーションすると以下のようになります。

ソースコード
import numpy as np
import pandas as pd

np.random.seed(777)

def GBM(mu, sigma, S0, dt, T):
    """
    simulates a geometric Brownian motion

    Parameters
    ----------
    mu : float
        expected return
    sigma : float
        volatility
    S0 : float
        initial stock price
    dt : float
        time increment
    T : float
        final time
    """
    # number of time increments
    N = int(T / dt)

    # time vector
    t = np.linspace(0, T, N + 1)

    # Brownian increments
    W = np.cumsum(np.random.standard_normal(N + 1)) * np.sqrt(dt)

    # geometric Brownian motion
    S = S0 * np.exp((mu - 0.5 * sigma**2) * t + sigma * W)

    # return the time and stock price paths as a tuple
    df = pd.DataFrame({"time": t, "price": S})
    return df


mu = 0.01
sigma = 0.03
dt = 1 / (252)

assets = [
    {
        "name": "asset" + str(i),
        "param": {
            "mu": mu * i,
            "sigma": sigma * i,
            "S0": 100,
            "dt": dt,
            "T": 30,
        },
    }
    for i in range(10)
]


df = pd.DataFrame()
for asset in assets:
    df[asset["name"]] = GBM(**asset["param"])["price"]
df.plot(figsize=(15, 8))

このコードは、株(i = 0, ..., 9)が、年率 1 * i %の収益率、年率 3 * i %のボラティリティ、初期株価100円、1日の時間刻みとして、30年間の株価をシミュレーションしています。

グラフを描くと以下のようになります。

株価

この記事では、この株価を使ってポートフォリオの最適化を行います。

リスクとリターン

この株価のデータから、リスクとリターンを計算します。

まず対数収益率を定義します。

X_t = \log {S_t / S_{t-1}}

年間の対数収益率はX_tの平均をとり年率に変換することで計算できます。年間のボラティリティは、X_tの標準偏差をとり年率に変換することで計算できます。

これをPythonで計算すると以下のようになります。

ソースコード
price = df["asset1"]
log_returns = np.log(price) - np.log(price.shift(1))
log_returns.dropna(inplace=True)

annual_return = log_returns.mean() * 252
annual_volatility = log_returns.std() * np.sqrt(252)

print("Annual return: {:.2f}%".format(annual_return * 100))
print("Annual volatility {:.2f}%".format(annual_volatility * 100))

このコードは、asset1の対数収益率を計算しています。また、年間の収益率とボラティリティを計算しています。

このコードを実行すると以下のようになります。

Annual return: 1.49%
Annual volatility 3.02%

asset1の年間の収益率は1.49%、ボラティリティは3.02%となりました。asset1が真に従う確率分布は、収益率1%でボラティリティ3%なので、この結果は真の値と近い値になっていることがわかります。

ちなみに、確率変数X_tの期待値は、\mu - \frac{\sigma^2}{2}です。この記事では、- \frac{\sigma^2}{2}の部分を無視して年間の対数収益率を計算しています。つまり年間の対数収益率を平均したものが、\muと同じ値になると近似しているということです。この近似は、\sigmaが小さいときには正確になります。今回の株価のデータでは、\sigmaが小さいので、この近似は正確になります。

ランダムポートフォリオ

次に、ランダムポートフォリオを作成して、リスクとリターンを計算します。ランダムポートフォリオとは、100円の資産をランダムに分配したポートフォリオのことです。

pythonで計算すると以下のようになります。

ソースコード
weights = np.random.random(len(assets))
weights /= np.sum(weights)

def portfolio_price(weights, df):
    return df[["asset" + str(i) for i in range(len(assets))]].mul(weights).sum(axis=1)

df["random_portfolio"] = portfolio_price(weights, df)

これを用いてランダムポートフォリオのリスクとリターンを計算します。

ソースコード
def portfolio_volatility(weights, df):
    price = portfolio_price(weights, df)
    log_returns = np.log(price) - np.log(price.shift(1))
    log_returns.dropna(inplace=True)
    std = log_returns.std() * np.sqrt(1 / dt)
    return std


def portfolio_return(weights, df):
    price = portfolio_price(weights, df)
    log_returns = np.log(price) - np.log(price.shift(1))
    log_returns.dropna(inplace=True)
    annual_return = log_returns.mean() / dt
    return annual_return

annual_return = portfolio_return(weights, df)
annual_volatility = portfolio_volatility(weights, df)

print("Annual return: {:.2f}%".format(annual_return * 100))
print("Annual volatility {:.2f}%".format(annual_volatility * 100))

このコードを実行すると以下のようになります。

Annual return: 2.73%
Annual volatility 7.57%

他の株と合わせて横軸をリスク、縦軸をリターンとしてプロットすると以下のようになります。

ソースコード
def calulate_summary(df):
    log_returns = np.log(df) - np.log(df.shift(1))
    summary = pd.DataFrame(
        {
            "return": log_returns.mean() / dt,
            "volatility": log_returns.std() * np.sqrt(1 / dt),
        }
    )
    return summary


summary = calulate_summary(df)

plt.figure(figsize=(15, 8))
plt.scatter(summary["volatility"], summary["return"])
for i in summary.index:
    plt.annotate(i, (summary["volatility"][i], summary["return"][i] - 0.002))
plt.xlabel("volatility")
plt.ylabel("return")
summary

ランダムポートフォリオ

このランダムポートフォリオは、全ての株の平均的なリターンを持ち、ボラティリティは全ての株の中で低い方に位置しています。投資家は、基本的に同じリターンを得るのであれば、リスクが低い方が良いと考えます。そのため、このグラフでは左上にあるポートフォリオが、良いポートフォリオといえます。そのため、今回のランダムポートフォリオは比較的良い位置にあるといえます。

効率的フロンティア

これまでの説明から、リスクとリターンの関係をプロットすることで、それぞれの投資戦略の良し悪しを判断することができることがわかりました。。また、ランダムポートフォリオのリスクとリターンも計算することができました。

投資の際には、同じリターンを得るのであれば、リスクを最小にしたいと考えます。そこで、ある収益を得るために必要なリスクを最小化するポートフォリオを探します。このようなポートフォリオは、効率的ポートフォリオと呼ばれています。効率的ポートフォリオのリスクとリターンの関係を効率的フロンティアと呼びます。[2]

定義に則り、効率的フロンティアを計算するコードを実装します。

ソースコード
from scipy.optimize import minimize

weights = (1 / len(assets)) * np.ones(len(assets))
bnds = tuple((0, 1) for x in range(len(assets)))
min_cagr, max_cagr = max(summary["return"].min(), 0), summary["return"].max()
target_cagr_list = np.linspace(min_cagr, max_cagr, 100)

volatilites = []
for target_cagr in target_cagr_list:
    constraints = [
        {"type": "eq", "fun": lambda weights: np.sum(weights) - 1},
        {
            "type": "eq",
            "fun": lambda weights: portfolio_return(weights, df) - target_cagr,
        },
    ]

    result = sco.minimize(
        portfolio_volatility,
        weights,
        args=(df,),
        method="SLSQP",
        bounds=bnds,
        constraints=constraints,
    )

    volatilites.append(result["fun"])
volatilites = np.array(volatilites)

plt.figure(figsize=(15, 8))
plt.scatter(summary["volatility"], summary["return"])
for i in summary.index:
    plt.annotate(i, (summary["volatility"][i], summary["return"][i]))
plt.xlabel("volatility")
plt.ylabel("return")
plt.plot(volatilites, target_cagr_list)

結果は次の通りです。

効率的フロンティア

この効率的フロンティア上のポートフォリオに投資することで、リスクを最小化しながら投資することができます。

等加重ポートフォリオ

これまでの説明から効率的ポートフォリオを選択することで、最小のリスクで収益を得ることができることがわかりました。ただこの分析には問題があります。それは、投資する際には未来のリターンやボラティリティを知ることができません。そのため、過去のデータを使って、未来のポートフォリオを作成することとなりますが、そのように作成したポートフォリオが未来でも効率的ポートフォリオであるとは限りません。

機関投資家は様々な情報を分析することで、そのリスクとリターンを推定し、効率的ポートフォリオに投資することができるでしょう。ただ、個人投資家にそのような情報分析を行うのは難しいです。そこで、等加重ポートフォリオという比較的簡単な方法でポートフォリオを作成します。等加重ポートフォリオとは、投資する株の数を等しくするポートフォリオのことです。そして、ランダムポートフォリオとこの等加重ポートフォリオを比較してみます。

まず、大量のランダムなポートフォリオを作成します。

ソースコード
# random portfolio

random_weights = np.random.random((1000, len(assets)))
random_weights = random_weights / random_weights.sum(axis=1, keepdims=True)
random_weights = pd.DataFrame(
    random_weights, columns=["asset" + str(i) for i in range(len(assets))]
)
random_summary = {"return": [], "volatility": []}
for i in random_weights.index:
    random_summary["return"].append(portfolio_return(random_weights.loc[i], df))
    random_summary["volatility"].append(portfolio_volatility(random_weights.loc[i], df))

次に、等加重ポートフォリオを作成します。

ソースコード
# equal weight portfolio

weights = np.ones(len(assets))
weights /= weights.sum()
equal_summary = {
    "return": portfolio_return(weights, df),
    "volatility": portfolio_volatility(weights, df),
}

これらのポートフォリオを効率的フロンティアと比較してみます。

ソースコード
# plot risk and return

plt.figure(figsize=(15, 8))

for i in random_summary:
    plt.scatter(random_summary["volatility"], random_summary["return"], c="red")

for i in summary.index:
    plt.annotate(i, (summary["volatility"][i], summary["return"][i]))
plt.scatter(summary["volatility"], summary["return"], c="black")

plt.scatter(equal_summary["volatility"], equal_summary["return"], c="blue")
plt.annotate("equal portfolio", (equal_summary["volatility"], equal_summary["return"]))

plt.xlabel("volatility")
plt.ylabel("return")
plt.plot(volatilites, target_cagr_list)

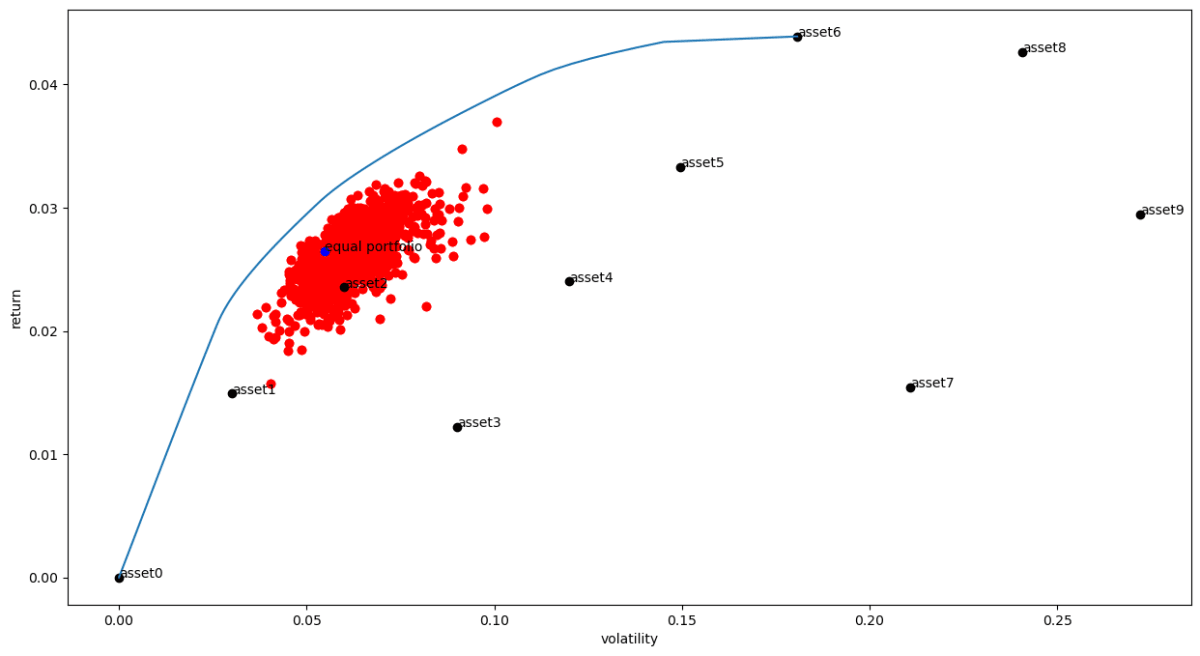
等加重ポートフォリオ

このグラフを見ると、ランダムポートフォリオは、左上の効率的フロンティアに近いポートフォリオが多く存在していることがわかります。また、等加重ポートフォリオは、ランダムポートフォリオの中でも効率的フロンティアに近いポートフォリオであることもわかります。この図から、まず例えランダムであったとしても、株を一つ買うより複数買った方がリスクが抑えられることがわかります。さらに、その中でも等加重ポートフォリオは、比較的良い位置に存在していることがわかります。

最後に、等加重ポートフォリオの価格のグラフを見てみます。

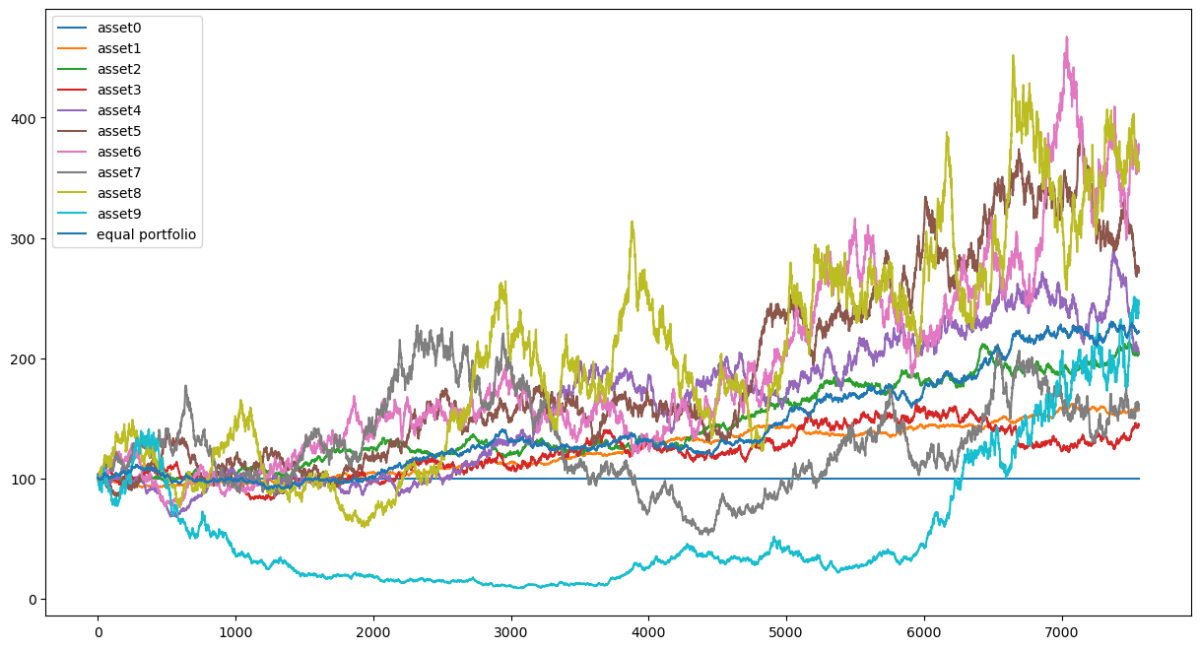
等加重ポートフォリオの価格

価格のグラフを見ると、等加重ポートフォリオの価格は、安定して上昇傾向にあることもわかります。

まとめ

この記事では、Pythonで株価のポートフォリオを最適化して効率的フロンティアを描きました。また、ランダムポートフォリオや等加重ポートフォリオを作成して、効率的フロンティアと比較しました。 株を単体で買うよりもランダムポートフォリオで買う方がリスクを抑えられることがわかりました。さらに、ランダムに選ぶより等加重ポートフォリオを選ぶ方が効率的フロンティアに近いポートフォリオを選べることもわかりました。

投資で何買うか迷ったら、目の前の選択肢の全てを等加重で買うと良いのかもしれません。

脚注

  1. https://ja.wikipedia.org/wiki/幾何ブラウン運動 ↩︎

  2. https://en.wikipedia.org/wiki/Efficient_frontier ↩︎

Discussion