🦋

Juliaで8x8の正方形を合同な4つの領域で分割する（その2）

2024/03/28に公開

Julia

math

idea

前回のまとめ

この記事は「Juliaで8x8の正方形を合同な4つの領域で分割する（その1）」の続きとなります。

Juliaで8x8の正方形を合同な4つの領域で分割する方法は以下の3パターンがあるようです。

そして，「90度回転して初めて重なるもの」は1191通りでした。（できた図を眺めていたら，裏返して重なるものがあるように思えました。重複している可能性があるので，これは改めて検討したいと思います。）

行列をプロット

8x8の正方行列からタイルに色を塗って表示します。正方行列の成分は0,1,2,3とします。描画パッケージPlots.jlを使いました。0は赤，1は青，2は緑，3は紫です。

関数の作成

# 描画パッケージ
using Plots

# 正方形のマス目のデータ作成
function rect_number(x::Int,y::Int)
    xval = [x-1,x,x,x-1,x-1]
    yval = [y-1,y-1,y,y,y-1]
    return xval,yval
end

# 8x8のマス目の塗る
function draw_rect(A= [rand(1:4) for i =1:4,j=1:4])
    plot(label=false,xlim=(-4,4),ylim=(-4,4),aspectratio=true,framestyle=:box,ticks=-4:1:4,showaxis=false)
    # A = [rand(1:4) for i =1:4,j=1:4]
    for i = 1:4 ,j = 1:4
        if mod(A[i,j],4) == 0
            plot!(rect_number(i,j),fill=true,color=:royalblue,label=false,alpha=.5)         #1
            plot!(rect_number(-j+1,i),fill=true,color=:forestgreen,label=false,alpha=.5)      #2
            plot!(rect_number(-i+1,-j+1),fill=true,color=:mediumorchid3,label=false,alpha=.5)   #3
            plot!(rect_number(j,-i+1),fill=true,color=:brown3,label=false,alpha=.5)           #4
        elseif mod(A[i,j],4) == 1
            plot!(rect_number(i,j),fill=true,color=:forestgreen,label=false,alpha=.5)      #2
            plot!(rect_number(-j+1,i),fill=true,color=:mediumorchid3,label=false,alpha=.5)   #3
            plot!(rect_number(-i+1,-j+1),fill=true,color=:brown3,label=false,alpha=.5)           #4
            plot!(rect_number(j,-i+1),fill=true,color=:royalblue,label=false,alpha=.5)         #1
        elseif mod(A[i,j],4) == 2
            plot!(rect_number(i,j),fill=true,color=:mediumorchid3,label=false,alpha=.5)   #3
            plot!(rect_number(-j+1,i),fill=true,color=:brown3,label=false,alpha=.5)           #4
            plot!(rect_number(-i+1,-j+1),fill=true,color=:royalblue,label=false,alpha=.5)         #1
            plot!(rect_number(j,-i+1),fill=true,color=:forestgreen,label=false,alpha=.5)      #2
        else 
            plot!(rect_number(i,j),fill=true,color=:brown3,label=false,alpha=.5)           #4
            plot!(rect_number(-j+1,i),fill=true,color=:royalblue,label=false,alpha=.5)         #1
            plot!(rect_number(-i+1,-j+1),fill=true,color=:forestgreen,label=false,alpha=.5)      #2
            plot!(rect_number(j,-i+1),fill=true,color=:mediumorchid3,label=false,alpha=.5)   #3
        end
     end
    plot!()
end

例

4×4 Matrix{Int64}:
0 0 0 1
0 0 0 1
0 0 0 0
0 0 0 0

A |> gen_matrix

8×8 Matrix{Int64}:
2 2 2 2 2 2 1 1
2 2 2 2 1 1 1 1
3 2 2 2 1 1 1 1
3 2 2 2 1 1 1 1
3 3 3 3 0 0 0 1
3 3 3 3 0 0 0 1
3 3 3 3 0 0 0 0
3 3 0 0 0 0 0 0

A |> draw_rect

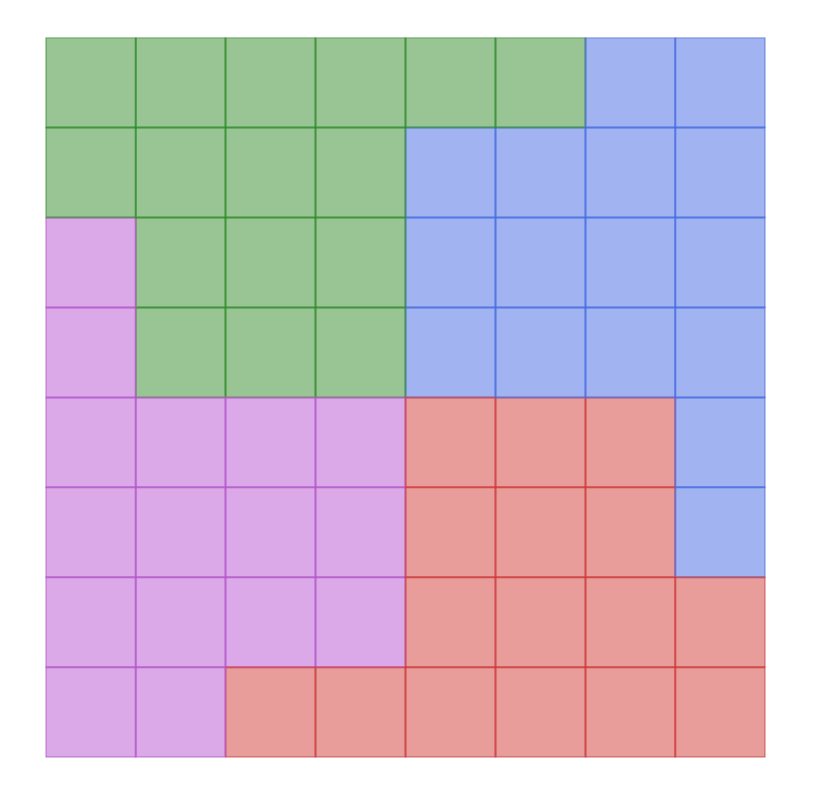
GIFアニメーションの作成

最後にGIFアニメーションの作成です。Xは1191個の4x4の行列のデータです。

using Plot
anim = Animation()
for i=1:1191
    plt = draw_rect(X[i])
    frame(anim, plt)
end
gif(anim, "90rotate.gif", fps = 1)

まとめ

とりあえず，重複のチェックと，他の2パターンの検討はありますが，大きいところは終わったので残りは後日とします。

＜続き＞