Juliaで8x8の正方形を合同な4つの領域で分割する(その1)
はじめに
Xで@takechan1414213 さんの次のような投稿がありました。
こういう,頭の体操はとても楽しいで,取り組んでみました。
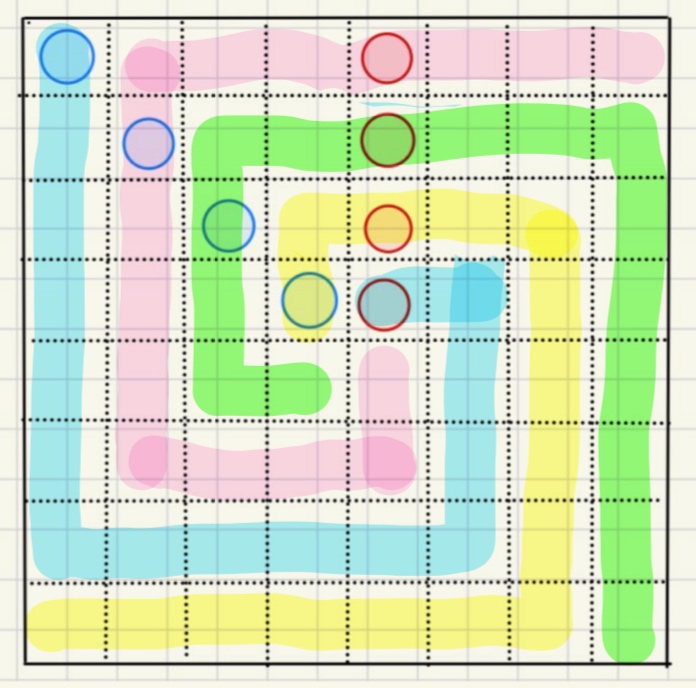
そこで,「8x8の正方形を合同な4つの領域で分割すると何パターンくらできるのだろう?」と思いました。早速実験です。
いくつかの例
今回は4色使うのでjuliaのロゴカラーを使うことにしました。
http://juliagraphics.github.io/Colors.jl/stable/namedcolors/#Julia-logo-colors
まずは4つ描いてみました。
これらは,90度回転すると重なる形です。これ以外にもあるのかな?と思っていると,@TQesprさんから
- 180度回転で初めて重なるもの
- 線対称(4x8の長方形2つ)であるもの
があることを教えてもらいました。
これらの3パターンで調べてみます。
90度回転で初めて重なる
とりあえず20個描いてみる
まずは,20個描いてみました。「これはいっぱいあるな」という感じです。
方針
個数も求めたいし,その時の配置も求めたいです。まずは次のような流れで考えました。
関数の作成
今回作った関数です。利用するパッケージはCombinatorics.jlです。
# コンビネーションパッケージ
using Combinatorics
# 行列を90度回転する
function rotate_matrix(matrix)
n = size(matrix, 1) # 行数(=列数)を取得
rotated = Matrix{eltype(matrix)}(undef, n, n) # 回転後の行列を初期化
for i in 1:n, j in 1:n
rotated[j, n-i+1] = matrix[i, j] # 90度回転させた位置に値を代入
end
return rotated
end
# 4x4の行列を90度ずつ回転して,8x8の行列を作る
function gen_matrix(A = Int.(zeros(4,4)))
E =Int.(ones(4,4))
B = rotate_matrix(-E+A)
C = rotate_matrix(-E+B)
D = rotate_matrix(-E+C)
X = mod.([
C D
B A
],4)
end
# 連結する部分が16個の行列を求める
function conti_16(A::Matrix) # 4x4の行列を入力 各成分は0,1,2,3
GA = gen_matrix(A) # 8x8の行列を生成
k = GA[1,1] # [1,1]成分
Pack = [[1,1]] # 連結する成分を加えていく
t = 1 # パラメータ
x = 16 # パラメータ
while t != x
for i = 1:8,j=1:8
if GA[i,j] == k
if [i-1,j] in Pack ||[i+1,j] in Pack ||[i,j-1] in Pack ||[i,j+1] in Pack
push!(Pack,[i,j])
end
end
end
x = t
t = Pack |> union |>length
end
P = Pack |> union
end
# 行列を用意して何個あるか調べます。
function count_16()
c = []
for i = 1:3
append!(c,[0,1,2,3])
end
c₂ = permutations(c,3) |> union
for t in c₂
pushfirst!(t,0)
end
b = []
for i = 1:4
append!(b,[0,1,2,3])
end
b₂ = permutations(b,4) |> union
X = []
for k₁ in c₂ , k₂ in b₂ , k₃ in b₂ , k₄ in b₂
A = Matrix([k₁ k₂ k₃ k₄]')
if conti_16(A) |> length == 16
println(A)
push!(X,A)
end
end
X
end
コードの実行
どのくらい時間がかかるかわからないのですが,とりあえず回してみることにしました。
環境はこんな感じです。
versioninfo()
Julia Version 1.10.2
Commit bd47eca2c8a (2024-03-01 10:14 UTC)
Build Info:
Official https://julialang.org/ release
Platform Info:
OS: macOS (arm64-apple-darwin22.4.0)
CPU: 8 × Apple M1
WORD_SIZE: 64
LIBM: libopenlibm
LLVM: libLLVM-15.0.7 (ORCJIT, apple-m1)
Threads: 1 default, 0 interactive, 1 GC (on 4 virtual cores)
X = count_16()
1191-element Vector{Any}:
[0 0 1 2; 0 1 1 2; 0 1 2 2; 1 1 2 2]
[0 0 1 2; 0 1 1 2; 0 1 2 2; 1 1 1 2]
[0 0 1 2; 0 1 1 2; 0 1 2 2; 1 1 1 1]
[0 0 1 2; 0 1 1 2; 0 1 1 2; 1 1 2 2]
[0 0 1 2; 0 1 1 2; 0 1 1 2; 1 1 1 2]
[0 0 1 2; 0 1 1 2; 0 1 1 2; 1 1 1 1]
[0 0 1 2; 0 1 1 2; 0 1 1 1; 1 1 1 1]
[0 0 1 2; 0 1 1 2; 0 0 1 2; 1 1 1 2]
[0 0 1 2; 0 1 1 2; 0 0 1 2; 1 1 1 1]
[0 0 1 2; 0 1 1 2; 0 0 1 1; 1 1 1 1]
⋮
[0 1 1 1; 0 0 0 1; 1 0 1 1; 1 1 1 1]
[0 1 1 1; 0 0 0 1; 1 1 0 1; 0 1 1 1]
[0 1 1 1; 0 0 0 1; 1 1 0 1; 1 1 1 1]
[0 1 1 1; 0 0 0 1; 1 1 1 1; 0 1 1 1]
[0 1 1 1; 0 0 0 1; 1 1 1 1; 0 0 1 1]
[0 1 1 1; 0 0 0 1; 1 1 1 1; 0 0 0 1]
[0 1 1 1; 0 0 0 1; 1 1 1 1; 0 0 0 0]
[0 1 1 1; 0 0 0 1; 1 1 1 1; 1 1 1 1]
[0 1 1 1; 0 0 0 0; 0 0 0 0; 0 0 0 0]
大体90分で終了です。1191通りでした。色については(1,1)を固定し,色の順番は固定されています。重複はないと思います。(ないと信じたい。続く)
ちょっとだけ紹介
100番目から107番目の8個を紹介します。ちゃんとできているようですね。
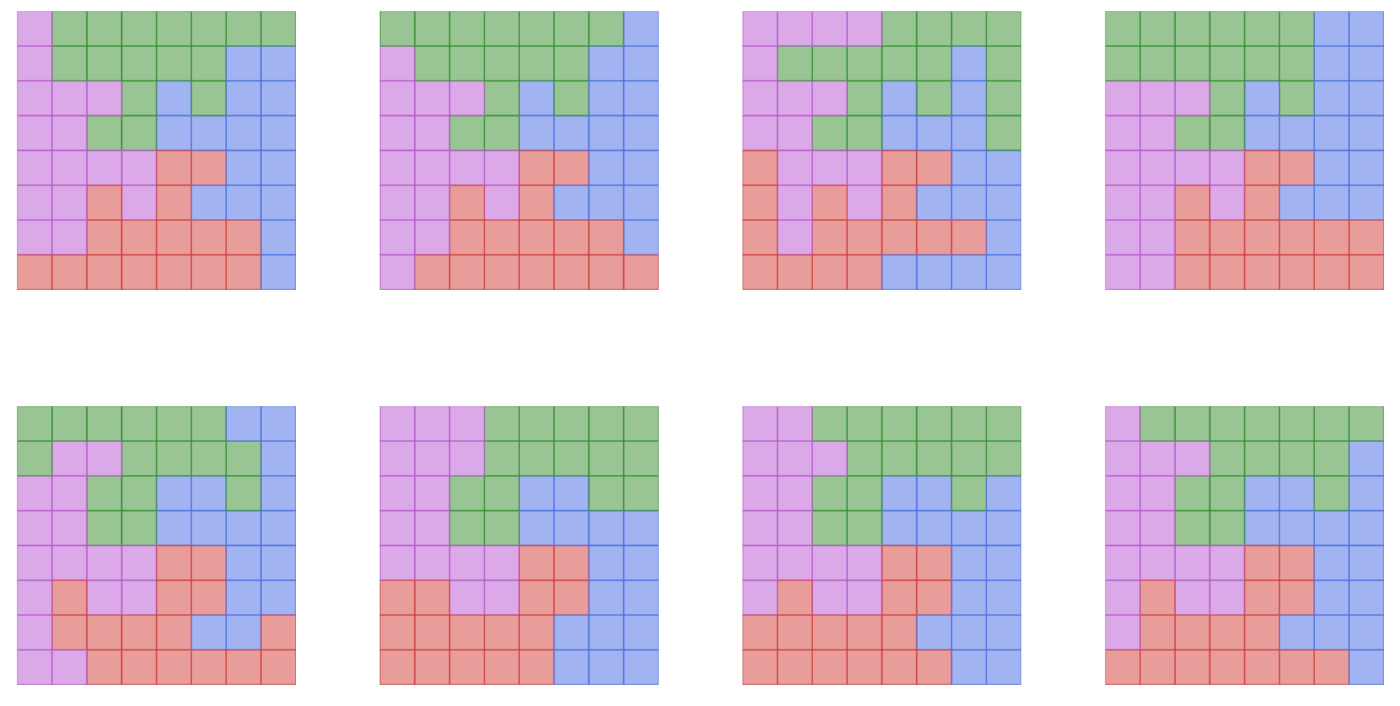
最後の1191番目は次のような感じです。
<続き>
Discussion
すでにそのような関数は Julia 標準に存在します!
rotr90()(左方向への回転ならrotl90())です。【追記】Claude(にせよ他の生成AIにせよ)、既存の標準ライブラリ関数を学習してないの前々から気になってるんですよね…。
やっぱりありますよね!ありがとうございました。