Flowベース生成モデルの調査

はじめに

はじめまして、株式会社D2C（以下D2C）で内定者アルバイトをしている井上です。
今年の4月から就職予定のD2Cで、現在生成AIの調査を行っています。
この記事では、Flowベース生成モデルに関する論文を紹介します。

記事は3つに分け、以下の内容で執筆します。
1. GAN, 拡散モデルの調査
2. Flowベース生成モデルの調査
3. 画像生成モデルの比較
この記事では、"2. Flowベース生成モデルの調査"についてです。

背景

昨今、ChatGPTの登場を皮切りに生成AIといった単語が広く一般層にも認知されるようになりました。
生成AIには、画像生成、テキスト生成、動画生成、音声生成など、いくつかの種類があります。このうち、画像生成AIに着目した場合、Stable DiffusionやDALL・E3などの登場により、誰でも簡単に高品質な画像の生成を行うことが可能になりました。一方で、この画像生成AIが将来的にクリエイターの仕事を奪うのではないか、AIの学習に大量にイラストが登用されるのでないかなどの問題があり、ネット上で議論になっていたりもします。

さて、そんな生成AIですが、なぜこれほどまでに高品質な画像を生成可能になったのでしょうか。それは　GANやDiffusion modelなどをはじめとした様々な画像生成モデルが提案されたことにあり、これらのモデルは日々加速度的に提案されています。
画像生成AIは実に様々なアプローチから高品質な画像を生成するモデルが提案されていますが、皆さんは、Flowベース生成モデル(以下、Flowモデル)というモデルはご存知でしょうか。

Flowモデルとは、尤度を直接計算可能でその尤度を最大化することで学習が可能なモデルになります。特に、ICLR2023に採択された「Flow Matching for Generative Modeling」は、Diffusion Modelよりも効率的に訓練・サンプリングができるモデルとして、ICLR2023のSpotlightに選ばれています。本記事では、「Flow Matching for Generative Modeling」の紹介をメインに行いますが、前提知識として理解しておいた方が良い「正規化Flow」及び「CNF: Continuous Normalizing Flows」の解説も簡単にですが行います。

目的

理想の生成モデルとは、高品質で多様な画像を生成できることとされています。
生成モデルである"GAN"、"拡散モデル"および"Flowモデル"について、どのモデルが高品質で多様な画像を生成できるか調べたなかから、この記事では、Flowモデルについて説明します。また、実際に実装、訓練および生成した結果を報告します。
​
またこの記事は、D2Cの内定者アルバイト生の活動内容を社外の方に知っていただくことを目的としています。
機械学習や深層学習について詳しくない方に読んでいただくために、各モデルの仕組みについては簡単な説明を心がけています。

記事の要約

本記事では大まかに３種類のFlowベースモデルを紹介しています。

正規化Flow

• 単純な確率分布を非線形で可逆な変換fを繰り返し適用し複雑な分布に変換する
• データ分布$p_x(x)$を直接学習すれば良い
• MNISTやTFDはそれなりに生成できているがSVHNやCIFAR-10の精度はイマイチ

CNF: Continuous Normalizing Flows

• 単純な確率分布から複雑な分布への変換を連続的（時刻0~1）な変換とし常微分方程式(ODE)を用いて解く
• 画像の品質が向上し、より複雑なデータ分布を捉えることが可能になるといったメリット
• 計算コストが高い

Flow Matching

• CNFを時刻ごとの学習が可能
• Diffsion modelのように計算プロセスを簡略化している
• OT(Optimal Transport)pathを利用すると少ないサンプリング数で生成可能（効率的に学習が可能）

Flowモデル

正規化Flowの仕組み

正規化フローで代表的な論文として、NICE(NON-LINEAR INDEPENDENT COMPONENTS ESTIMATION) Laurent Dinh et al. 2015 が挙げられます。NICEとは、ICLR2015に採択された論文であり、Flow系論文の始祖的な論文に位置しています。

正規化Flowの手法としては、簡単な形（ガウス分布など）の確率分布$q(z)$に対して、非線形で可逆な変換fを繰り返し適用することで複雑な分布$q(z)$を表現します。（図１参照）　ただし、fは可逆かつヤコビ行列式が簡単に計算できなければならないという条件があります。
ちなみに、このfによる$z$~$p_z(z)$の流れのことをFlowと呼びます。

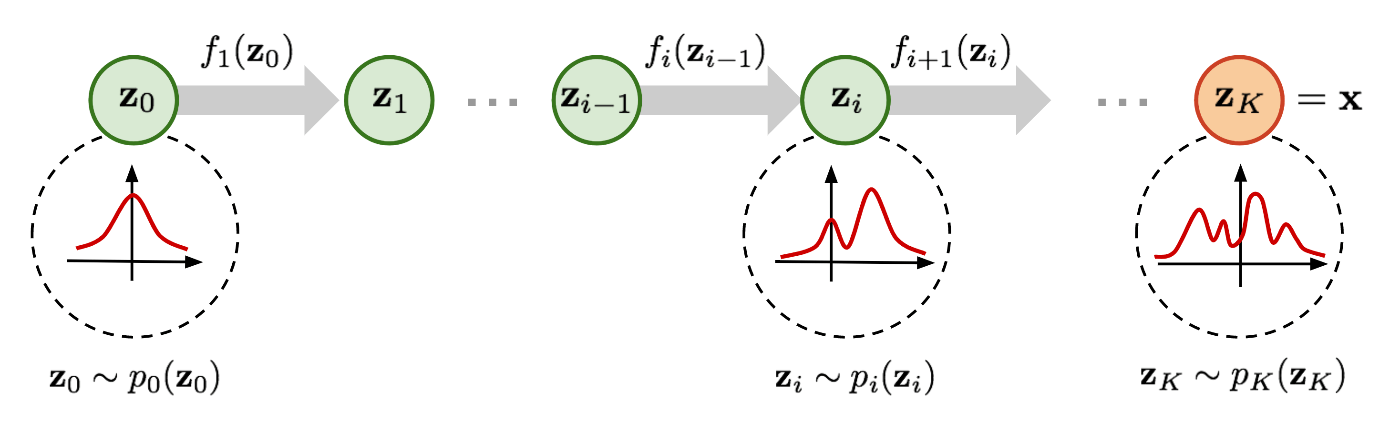
図１：単純な分布$p_0(z_0)$を段階的に複雑な分布$p_K(z_K)$に変換する正規化フローモデル(出典：https://lilianweng.github.io/lil-\log\2018\10\13\flow-based-deep-generative-models.html)

生成モデルのアプローチとして、真の分布（データ分布）$P_{data}(x)$と近いモデル分布を求めたい時、KLダイバージェンスで分布間の距離を測ります。

図２：$P_{data}(x)とP_θ(x)分布間のイメージ図$

$$\begin{aligned} D_{KL}[P_{data}(x)||P_0(x)] &= \int P_{data}(x)\log \frac{P_{data}(x)}{P_θ(x)}dx \\ &= \int P_{data}(x)\log P_{data}dx - \int P_{data}(x)\log p_θ(x) \end{aligned}$$

2項目の対数尤度関数の期待値を最大化して分布に近づくように学習を行います。
この様にして学習された正規化Flowモデルの生成例は図３の様になります。MNISTやTFDはそれなりに生成できているのに対してSVHNやCIFAR-10は精度良く生成できていないことがわかります。特に、CIFAR-10に関しては、正規化Flowよりも前に発表されたGANの方が高精度に生成できています。




図3：NICEモデルの生成例（出典：　https://arxiv.org/pdf/1410.8516.pdf　）

CNF: Continuous Normalizing Flowsの仕組み

「CNF: Continuous Normalizing Flows」の代表的な論文として、「Continuous-Time Flows for Efficient Inference and Density Estimation(Changyou Chen et al. 2017)」 や「Neural Ordinary Differential Equations(Ricky T. Q. Chen et al. 2018 )」(以下、Neural ODE)などが挙げられます。

Neural ODEは、ニューラルネットワークで常微分方程式　(ODE)を解く手法です。
このNeural ODEの論文内で「CNF: Continuous Normalizing Flows」が触れられています。
正規化Flowでは、非線形で可逆な変換fを繰り返し適用することで複雑な分布$q(z)$を表現していました、CNFでは、それらの変換を連続的(時刻0~1)な変換としODEを用いて解きます。

$$\begin{aligned} \frac{d}{dt}\varPhi_t(x) &= v_t(\varPhi_t(x)) \\ \varPhi_0(x) &= x \end{aligned}$$

メリットとして、NNで採用できる層が不可逆変換でもよくなりモデルの自由度が上がる他、画像の品質が向上し、より複雑なデータ分布を捉えられる点が挙げられます。一方で、ODEの解法の計算コストが高く、実用的な応用においては不便といったデメリットも存在します。

生成された画像例が図4のようになります。正規化Flowと比較し生成画像の品質が向上していることが確認できます。

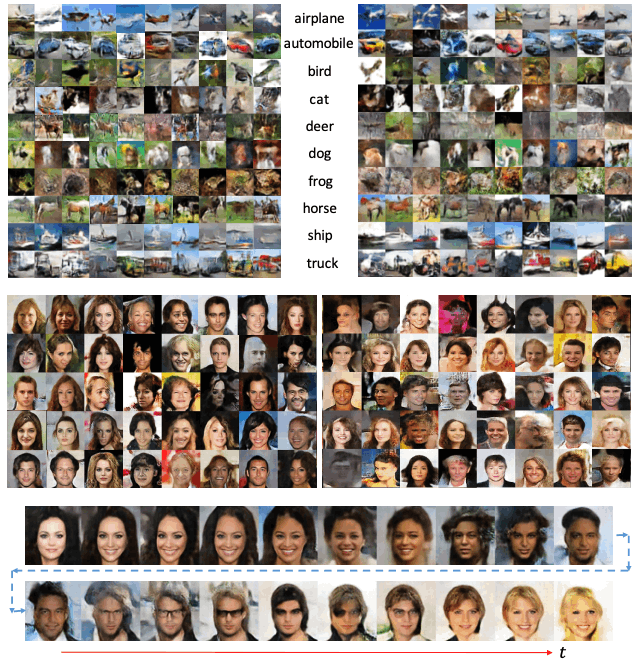
図4:CNFの画像生成例（出典：https://arxiv.org/pdf/1709.01179.pdf　）

Flow Matchingの仕組み

Flow Matchingでは、CNF（Continuous Normalizing Flow）を各時刻の条件付フローで学習します。
目的確率密度分布$p_t(x)$と$p_t(x)$を生成するベクトル場$u_t(x)$が与えられたとき、Flow Matching(以下、FM)は、以下のような式で求められます。

$${\mathcal L}_M(θ)={\mathbb E}_{t,Pt_(x)}||v_t(x)-u_t(x)||^2 \tag{1}$$

ここで、θはCNFベクトル場$v_t(x)$の学習可能なパラメータ、$t〜U[0,1]$(一様分布)、$x=p_t(x)$を表します。つまり、FM損失はベクトル場$u_t$をニューラルネットワーク$v_t$で回帰し、損失がゼロになると、学習されたCNFモデルは$p_t(x)$を生成するということになります。したがって、Flow Matchingでは、CNFの定める$u_t$を$v_t$に近似させます。

流れは以下のようになります。
例えば、ある未知のデータ分布$q(x_1)$に従って分布する確率変数を$x_1$とし、データサンプル$x_1$が与えられたとき、

$$P_0(x|x_1)=P(x) \tag{2}$$

　

$$p_1(x|x_1)={\mathcal N}(x|x_1,σ^2I)\tag{3}$$

$$(σ<<1)$$

をみたす$P_t(x|x_1)$考えます。
ここで、$p_1(x|x_1)={\mathcal N}(x|x_1,σ^2I)$、$x_1$の平均と十分に小さい標準偏差 $σ>0$を持つ正規分布です。 $q(x_1)$上の条件付き確率分布を周辺化(marginalization)すると，次のような境界確率分布(marginal probability path)が得られます。

$$p_t(x)=\int p_t(x|x_1)q(x_1)dx_1\tag{4}$$

特に時間$t=1$では、周辺確率$p_1$はデータ分布$q$に非常に近似する混合分布となります。

$$p_t(x)=\int p_t(x|x_1)q(x_1)dx_1\approx q(x)\tag{5}$$

条件付きベクトル場を「周辺化(marginalization)」することで、conditional vector fieldsを定義できます。（全ての$t$と$x$について$p_t(x)>0$と仮定）

$$u_t(x) = \int u_t(x|x_1)\frac{p_t(x|x_1)q(x_1)}{p_t(x)}dx_1\tag{6}$$

条件付き確率分布$p_t(x|x_1)$を生成するベクトル場$u_t(x|x_1)$が与えられたとき、任意の分布$q(x_1)$に対して、式6のconditional vector fields $u_t$は式4の境界確率分布(marginal probability path) $p_t$を生成しています。（論文内の定理１）

しかし、境界確率分布(marginal probability path)とベクトル場の定義（式4と式6）には、扱いにくい積分があるため、$u_t$を計算することは依然として困難であり、その結果、元のフローマッチング目的変数の不偏推定量を単純に計算することも困難です。そこで、筆者らは、以下のようなよりconditional Flow Matching（以下、CFM）の目的変数を提案しています。

$${\mathcal L}_{CFM}(θ)={\mathbb E}_{t,q(x_1),P_t(x|x_1)}||v_t(x)-v(x|x_1)||^2 \tag{7}$$

FMの目的変数とは異なり、CFMの目的変数では、$p_t(x|x_1)$から効率的にサンプリングし、$u_t(x|x_1)$を計算することができる限り、不偏推定値を簡単にサンプリングすることができます。つまり、$u_t$へのFMは、CFMと同値となります。（論文内の定理2）
これにより、境界確率分布(marginal probability path)や境界ベクトル場（marginal vector field）にアクセスすることなく、境界確率分布$p_t$（特に$t=1$における未知のデータ分布$q$）を近似するCNFを訓練することができるようになります。

条件付き確率分布とベクトル場

条件付き確率分布がガウシアンで与えられたとき、条件付きベクトル場は以下のように表せます。

$$p_t(x|x_1)={\mathcal N}(x|μ_t(x_1),σ_t(x_1)^2I)\tag{8}$$

ここで、$μ_t$が時刻tの平均であり、$σ_t$が時刻tの標準偏差を表しています。
任意の特定の確率分布を生成するベクトル場は無限に存在しますが、これらの大部分は、基礎となる分布を不変のままにしておく成分の存在によるものです。例えば、分布が回転不変である場合の回転成分など、不必要な計算につながります。筆者らは、ガウス分布の正準変換（canonical transformation）に対応する単純なベクトル場を使用しています。

$$ψ_t(x)=σ_t(x_1)x+μ_t(x_1)\tag{9}$$

$x$がガウス分布のとき、$ψ_t(x)$は平均$μ_t(x_1)$と標準偏差$σ_t(x_1)$を持つ正規分布の確率変数にマップするアフィン変換となり、$p_t(x|x_1)$を式(8)のようなガウス確率分布、$ψ_t$を式（９）のように対応するフローマップとすると、$ψ_t$を定義するユニークなベクトル場は次のようになります。（論文内の定理3）

$$μ_t(x|x_1)=\frac{σ^{\prime}_t(x_1)}{σ_t(x_1)}(x-μ_t(x_1))+μ^{\prime}_t(x_1) \tag{10}$$

ガウス条件付き確率分布の実例

例１：拡散条件付きベクトル場(Diffusion conditional Vector Fields)
拡散モデルは、データに徐々にノイズを付加する拡散過程と、徐々にノイズを除去する逆拡散過程を考慮することで高精度な画像を生成することが可能なモデルです。詳しくは、前回の記事をご参照ください。
例えば、ノイズからデータのVariance Exploding (VE)分布は、次のような形になります。

$$P_t(x|x_1)={\mathcal N}(x|x_1,σ^2_{1-t}I)\tag{11}$$

ここで、$σ_t$は増加関数、$σ_0=0$、$σ_1>>1$となります。式11は、$μ_t(x_1)=x_1$及び$σ_t(x_1)=σ_1-t$とし、これらを定理3の式10に代入すると、以下のようになります。

$$v_t(x|x_1)=-\frac{σ^{\prime}_{1-t}}{σ_{1-t}}(x-x_1) \tag{12}$$

逆（ノイズからデータ）Variance Preserving (VP) は、

$$P_t(x|x_1)={\mathcal N}(x|α_{1-t}x_1,(1-α^2_{1-t})I),\mathrm{where} \ \ α_t=e^{-\frac{1}{2}T(t)},T(t)= \int_{0}^{t}β(s)ds \tag{13}$$

となり、$β$はノイズスケール関数となります。$μ_t(x_1)=α_{1-t}x_1$、$α_t(x_1)=\sqrt{1-σ^2_{1-t}}$とし、これらを定理3の式10に代入すると以下のようになります。

$$v_t(x|x_1)=\frac{σ^{\prime}_{1-t}}{1-σ^2_{1-t}}=-\frac{T^{\prime}(1-t)}{2}\lbrack\frac{e^{-T(1-t)}x-e^{\frac{1}{2}T(1-t)}x_1}{1-e^{-T(1-t)}}\rbrack \tag{14}$$

この条件付きVF$u_t(x|x_1)$は、条件付き拡散プロセスに限定した場合、deterministic probability flow[Song et al. 2020]で使用されたVFと一致します。

例2：最適輸送条件付きベクトル場(Optimal Transport conditional VF)
$μ_t(x)=tx_1$, $σ_t(x)=1-(1-σ_{min})t$としたとき、定理3より、VFは以下のようになります。

$$v_t(x|x_1)=\frac{x_1-(1-σ_{min})x}{1-(1-σ_{min})t}\tag{15}$$

これは、最適輸送（OT：Optimal Transport）の displacement interpolantMaCann(1997)にあたるベクトル場みたいです。

図5：Diffusion pathの条件付きスコア関数とOT pathの条件付きベクトル場の違い
青は大きさ、赤は小ささを表す。
（出典：　https://openreview.net/pdf?id=PqvMRDCJT9t　）

図5は、拡散条件付きスコア関数（典型的な拡散法における回帰ターゲット）すなわち、式14のように定義された$p_t$を持つ$∇\log p_t(x|x_1)$と、OT条件付きVF（式15）を比較したものになります。

開始点($p_0$)と終了点($p_1$)は両方の例で同じです。注目すべきは、OT VFが時間的に一定の方向を持つことで、このことから、より単純な回帰タスクになっていることがわかります。この特性は、VFが$u_t(x|x_1)=g(t)h(x|x_1)$の形で書けるので、式15から直接検証することも可能です。また、「条件付きフローは最適であるが、これは決して境界VFが最適輸送解であることを意味しないことに注意しなければならない」と筆者らは、述べています。

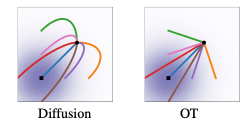
図6：拡散及びOT条件付き軌道（出典：　https://openreview.net/pdf?id=PqvMRDCJT9t　）
直感的に、OT変位マップ下の粒子は常に直線軌道で一定の速度で移動します。図6は、拡散VFとOT条件VFのサンプリング分布を示しています。拡散パスからのサンプリング軌道は最終サンプルを「オーバーシュート（※最小値を通り過ぎること）」する可能性があります。そのため、不要な後戻りを引き起こす一方で、OTパスでは直線的に進むことが保証されています。

利点と欠点

前回の記事で紹介したGAN及び拡散モデルと本記事にてメインで紹介したFlow Matchingの利点と欠点になります。

モデル	利点	欠点
GAN	・生成速度が速さ ・高精度の画像生成が可能	・訓練の不安定性
拡散モデル	・訓練の安定性 ・高精度の画像生成が可能	・生成速度の遅さ
Flow Matching	・拡散モデルより効率的に訓練とサンプリングが可能	・生成速度の遅さ(拡散モデルより速くGANより遅い)

実験

本章では、前章までの理論をもとに実際に実装、訓練および生成した結果を紹介します。
データセット及び前処理は、前回と同様です。前回の記事はこちら

訓練パラメータ

モデル	学習率	バッチサイズ	ステップサイズ
Flow Matching	1e-3	1000	100

​
Flow Matchingの$v_t$を求める際のU-Netはこちらを参考にしました。
実装はpytorch、最適化手法はAdamを使用しました。

訓練結果

生成画像

​
損失の推移を図７に生成画像例を図８に示します。
図７は縦軸がloss横軸がepochになります。epochが増えるごとにlossが減少していることがわかります。

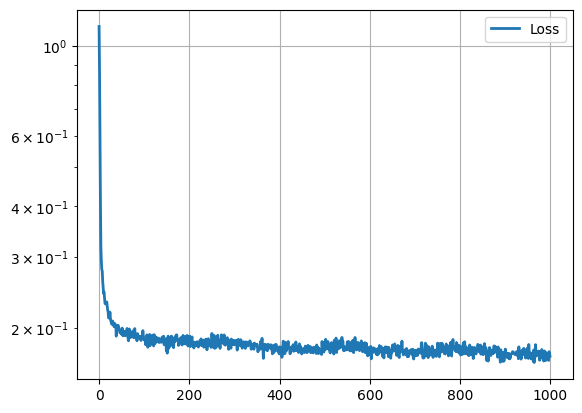
図7:損失の推移

まだ、若干ぼやけていますがそれらしい画像が生成されています。学習時に正規化しているのでその影響でぼやけているかもしれません。なお、Flowモデルの論文内ではもう少し綺麗に画像が生成されています。興味のある方は元論文をご確認ください

図8:学習したFlowモデルの生成した画像

調査した感想と結び

本記事では、Flow Matching for Generative Modelingを中心にFLowモデルの紹介を行いました。
私自身、GANやDiffusion modelなどは知っていたのですが、Flowモデルについては今回の論文調査や実装を通じて理解を深めることができました。今回は、Image to Imageの画像生成について調査しましたが、Stable DiffusionをはじめとするText to Imageでの画像生成では、Difuusion modelベースの画像生成モデルとCLIPと呼ばれる画像にテキストラベルをつけてクラス分けを行うモデルを組み合わせています。今後はこれらTetx to Imageをはじめとした様々な生成AIについて調査を行いたいと考えています。