Closed1
Attentionの近似計算手法の近況
Kernel法を基礎とした理論的なアプローチの近況をキャッシュしておく。
Attentionの分解
Attentionの計算には(1)式の行列積が出てくるが、kernelをQに起因する部分とKに起因する部分で分解することができれば、行列の計算順序を(QK)VからQ(KV)に変更することでlong contextの場合に計算機リソースを節約することができることが知られている。
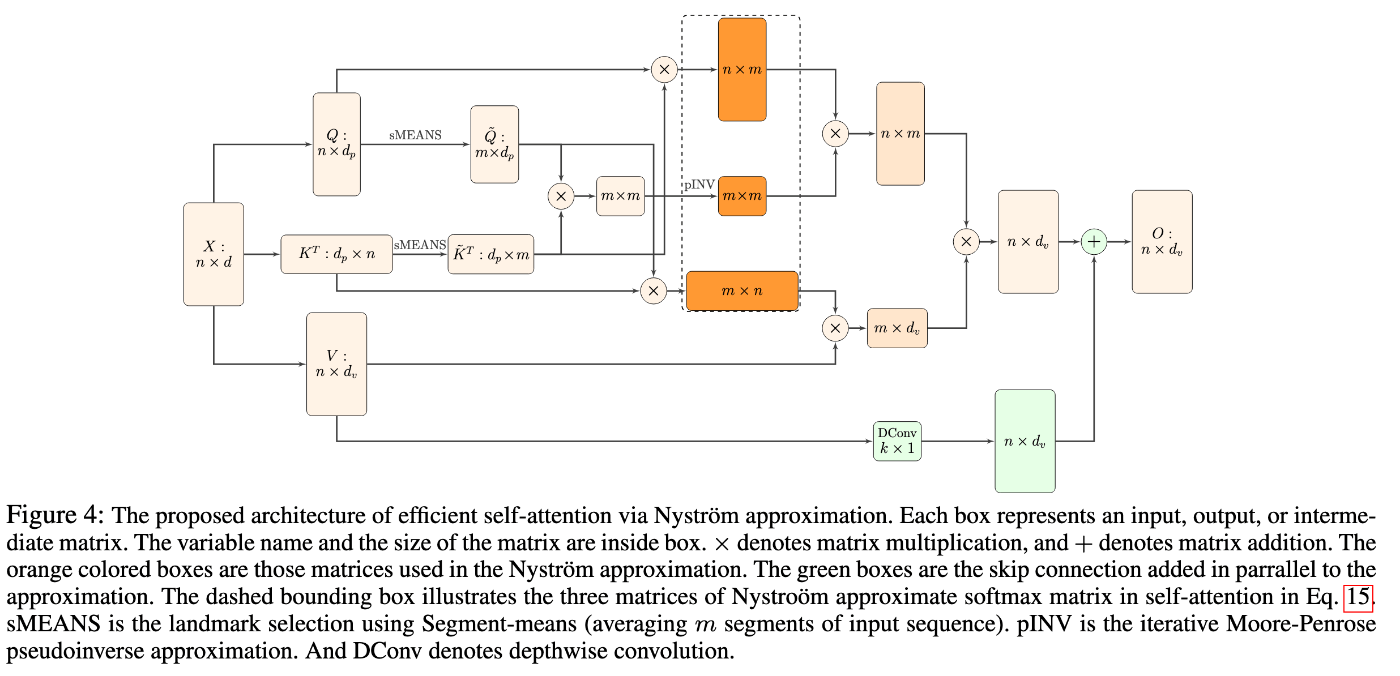
Nystromformer
Skyformer[1]の元となった手法。
アーキテクチャとベンチマーク結果は以下。

Skyformer
Nystromformerの近似計算法をベースとして、KernelにSoftmaxの代わりにGaussian Kernelを採用した。
個人的に面白いと思ったのが、オリジナルのSoftmax KernelとGaussian Kernelの関係性を指摘している点。
(4)式のように、正規化前のattentionの行列は1) Q-Kの埋め込みベクトルのガウス距離に依存する部分と2) Q, Kの絶対値に起因する部分に分解できる。前者はまさにQ-Kペアの類似度に相当する部分で、ベクトルの類似度を計測するのとAttentionの計算には密接した関係がある。
論文では後者の項が正規化の役割を果たしていて、Softmax正規化をしなくても学習の安定に寄与すると主張している。
Reference
このスクラップは2024/08/19にクローズされました