Attentionと類似度は異なるという話

はじめに

「Transformerのattentionはトークン間の類似度をモデリングしている」という説明をよく聞くが、この表現は適切でないことを示す。

なお、このような説明がよくされる背景としては、Transformerのdot-product attentionは内積で計算され、コサイン類似度も正規化されたベクトルの内積で計算される点によるものと思われる。しかしながら両者は正規化の有無に違いがあり、ベクトル空間に埋め込んだ時の数学的性質はかなり異なるということを本稿では指摘する。

TL; DR

• Attention(dot-product attention)は類似度とは異なる数学的性質を持つ
• 類似度はトークン間の近接関係はモデリングできるが、それ以外の多様な関連をモデリングするには適さない。
• dot-product attentionはトークン間の近接関係を含むさまざまな関連をモデリングするのに適する。

記事公開後にGaussian Kernelでsoftmax attentionと同等の性能を実現できたとする論文[4]、およびcosine類似度によるattention[5]の論文を見つけたので、「ベクトルの距離に基づくkernelはトークンの関連をモデリングするのに適さない」とするこの記事の主張は誤りであると思われます。しかしながら、埋め込み空間上でのkernelの値の分布についての考察はそれなりに意味があると考えるので記事自体は削除せずに残しました。

前提知識

AttentionはKernel関数の一種である

Transformerのdot product attentionはKernel関数によって定式化できる。Kernel関数とは、2つの $d$ 次元ベクトルをscalarにマップする関数として定義される:

$$k(x_0, x_1) \mapsto y \ge 0: \mathcal{R}^d \times \mathcal{R}^d \rightarrow \mathcal{R} \tag{1}$$

なお、機械学習の文脈で数学的に扱いやすい性質を持つkernel関数として正定値(positive definite)という性質のものがよく用いられるが、ここでは分かりやすさを重視して非負の値を持つものとして定義した。

Kernelの具体的な構成方法

具体的なKernel関数の構成方法について示す。

距離に基づくKernel

このカテゴリのKernelはベクトル同士の距離が近いものほど大きな値をとるという性質を持つ。すなわち、ベクトルの類似度の一種と言える。

Gaussian Kernel

$$k(x _ 0, x _ 1) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp \left( - \frac{\vert\vert x _ 0 - x _ 1 \vert\vert_2^2}{2\sigma^2} \right) \tag{2}$$

内積に基づくKernel

距離ではなく内積によってもKernelを構成できる。dot product Attentionは以下で定義されるExponential Kernelをコンテクスト内の全トークンで正規化して確率にしたものである。

Exponential Kernel

$$k(x _ 0, x _ 1) = \exp\left( \frac{ \langle x _ 0, x _ 1 \rangle }{\sqrt{d _ k}} \right) \tag{3}$$

Dot-product Attentionと類似度の違いについて

異なるKernel関数のベクトル空間上での数学的な性質の違いについて議論する。

距離に基づくKernel（類似度）の場合

Fig1は2次元ベクトル空間においてGaussian Kernelの値の等高線を示したものである。これによると、関連性の高いベクトルのペアの埋め込みについて以下の性質を持つ（この性質はGaussian Kernelに限らず、ベクトルの距離に基づいて定義されるkernel全般に成り立つことに注意）。

1. Kernelが最大値を取るのは2つの入力ベクトルが一致する場合で、その時に限る。
   

学習が進につれて関連性の高いトークンはベクトル空間内で1点に収束しようとする。従って、初期状態でさまざまな方向を向いていた関連トークンの埋め込みは学習の進行とともに多様性を失い、多様な関連の情報を空間内に埋め込む余地がなくなると考えられる。

この性質は時系列タスクにおけるトークン間の多様な特徴を捉えるには向いていないと言える。

冒頭に示した通り、この主張は誤りであると思われます。

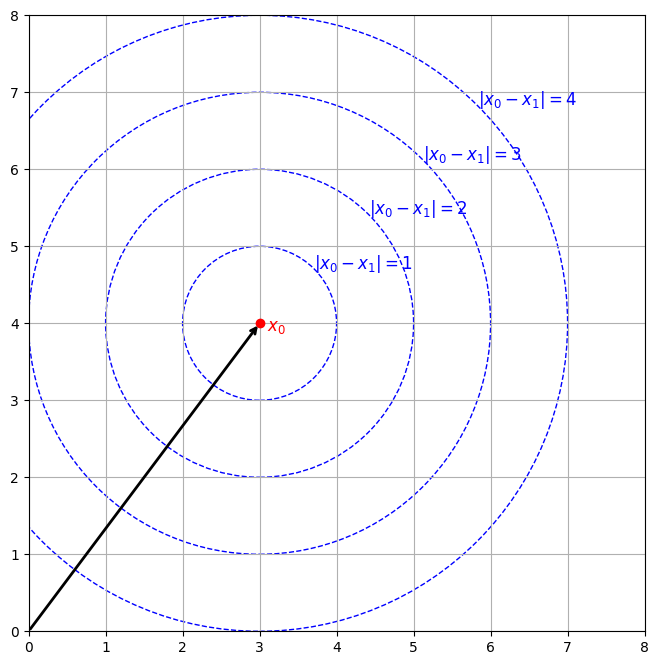
Fig.1 L2距離の等高線: L2距離が最小になる点は1点のみ

内積に基づくKernel（dot product attention）の場合

Fig2は2次元ベクトル空間におけるExponential Kernelの値の等高線を示したものである。これによると、

1. Kernelの値に最大値や最小値はない
2. 同じベクトル同士のペアがKernelの最大値を取る訳ではない（ $k(x_0, x_0) < k(x_0, x_1)$ なる $x_1$ が無数に存在する）。

距離に基づくKernelの場合と異なり、学習が進んでも関連性の高いトークンのベクトルは $x_0$ と直行する平面上に無限の広がりを持って分布することができる。また、学習できる関連の大きさに上限はなく、またベクトルの方向も元のトークンの方向とある程度独立しているので、学習が進んでもさまざまな関連の情報を空間内に保持し続けると考えられる。

なお、cosine類似度のように正規化された内積の場合はL2距離に基づくKernelと同様な性質を示すので、こちらも時系列タスクのAttentionの候補としては向いていないと言える。

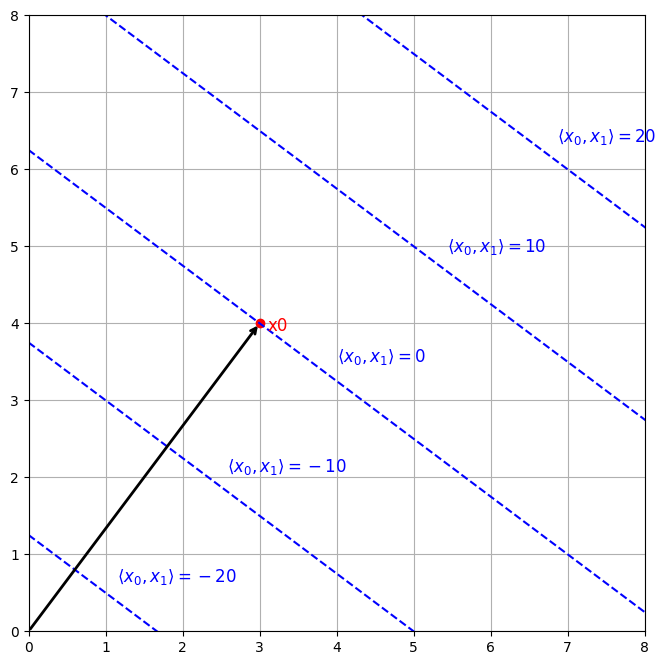
Fig.2 dot productの等高線: dot productが同じになる点は無数に存在する

関連研究

[1]はtransformerのdot-product attentionがカーネル関数によって定式化できることを示した先駆的な研究。

後続の研究として、[2, 3]ではSoftmax(Exponential Kernel)とは異なるkernelによってTransformer blockの代替を提案した。これらの研究では正定値Kernelを仮定することで、2変数入力のKernel関数を1変数関数の積に分解できるという定理を用いてQKV積の計算順序を(QK)VからQ(KV)に変換することでコンテキスト長が長い場合にメモリ消費と計算量を減らせるという実用的なメリットを提示した。具体的にはコンテキスト長を $M$, 次元を $d$ とするとメモリ消費と計算量は $O(M^2d)$ から $O(Md^2)$ になる。すなわちトークン長の寄与が2乗から線形になるので、トークン長が非常に長い場合 ($M \gg d$)は大きな計算機リソースの削減を期待できる。

$$k(Q_i, K_j)V_j = \phi(Q_i) \phi(K_j) V_j \tag{4}$$

参考文献

1. Transformer Dissection: A Unified Understanding of Transformer's Attention via the Lens of Kernel
2. cosFormer: Rethinking Softmax in Attention
3. DiJiang: Efficient Large Language Models through Compact Kernelization
4. Skyformer: Remodel Self-Attention with Gaussian Kernel and Nyström Method
5. Query-Key Normalization for Transformers