object detectionタスクのdynamic label assignmentに関する近年の研究成果についての補遺

概要

近年におけるobject detectionタスクの研究では、提案boxに正例、負例のラベルを割り当てる処理（label assignment）をモデルの内部状態に基づいて動的に行うdynamic assignmentが主流となっていることを以前書いた記事で述べた。

https://zenn.dev/bilzard/articles/label-assignment-in-object-detection

本稿ではdynamic label assignmentに関する比較的最近(2019年以降)の研究成果のうち、以前の記事で扱わなかったものについて補足する。

前提知識

本稿の内容を理解するにあたって以下の2点について説明する。

1. "anchor"という用語について
2. anchor-based手法における2種類の予測boxについて

"anchor"という用語について

Object detection界隈の論文では"anchor"という言葉が複数の意味で用いられているようなので本項では以下のように定義する。

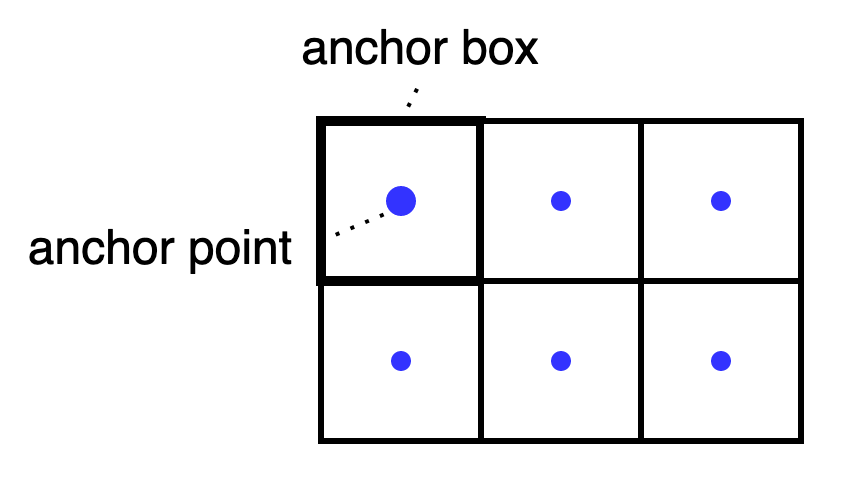
• anchor point: 候補boxの生成の元となるfeature map上の点。
• anchor box: anchor pointを中心とするfeature map上の1/n x 1/nの区画。

文脈から推察できる場合は上記をともに「anchor」と呼ぶ。そうでない場合は上記の明示的な呼び方を用いる。

anchor-based手法における2種類の予測boxについて

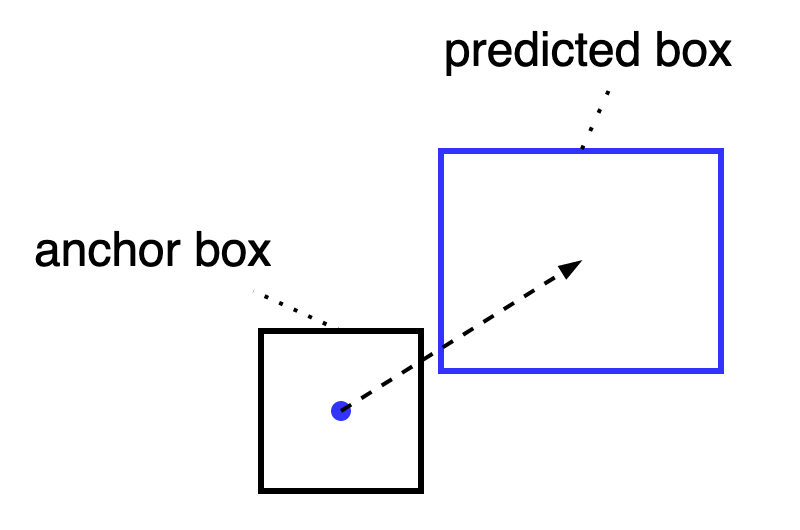
anchor-basedなobject detection modelは、本質的に以下の2段階の予測boxを行っているとみなせる。

1. anchor box: anchor box自体。
2. predicted box: anchor pointのembeddingをもとに回帰ヘッダにより予測されるより正確なboxのこと。

実際、ATSS[1]ではanchor boxとGTとのIoUに基づいてlabel assignmentを決定しているので、anchor boxを「1段階目の粗い予測」として活用している。本稿では可能な限り両者を区別して表記するが、文脈から想定できる場合は単にboxと表記する。

label assignment に predicted boxを利用する

ATSS[1]ではlabel assignmentにおけるboxの評価値をanchor boxとGTとのIoUに基づいて計算していた。

これに対し、DLA[7]はanchor boxとGTとのIoU(AIoU)に加えて、回帰ヘッダの出力する予測boxとGTとのIoU(PIoU)も加味して評価値を計算する。

Anchor boxは学習可能なパラメータを持たないため、モデルの学習状態を加味してboxの評価を決定することができない、一方、回帰ヘッダが予測するboxはモデルの学習状態を反映しているため、より正確な評価ができると考えられる。

その一方で、学習の初期段階においては回帰ヘッダの予測するboxの評価値は信頼できず、anchor boxに基づく評価値がよりモデルの学習の助けになると考えられる。

このような考察から、DLAではAIoUとPIoUを組み合わせたassignment方針をとる。
具体的にはGT付近のPIoUとAIoUのスコアの平均と分散をそれぞれ独立して算出し、両者を足し合わせた以下の式により閾値を動的に決定する。

$$\begin{align*} \text{threshold} &:= \mu_\text{CIoU} + \sigma_\text{CIoU} \\ \mu_\text{CIoU} &:= \mu_{\text{AIoU}} + \mu_{\text{PIoU}} \\ \sigma_\text{CIoU} &:= \sigma_{\text{AIoU}} + \sigma_{\text{PIoU}} \end{align*}$$

class予測タスクにlocalityの評価を組み込む

Object detectionの研究論文では伝統的にpost processにNMS(Non Maximum Suppression)が使用されることが多い。NMSではモデルの予測するboxの評価値に基づいて、重複したboxのうち評価値の高いboxのみをのこす処理を行う。boxの評価値をどのように設計するかについては試行錯誤の余地がある。一般的にはクラスの予測確率とboxの位置の精度の評価値(locality)に基づいて行われることが多い。

例えば、FCOSではboxのlocalityの評価値としてGTと予測boxとのIoUを予測する独立したheadをもち、推論時にclassの予測確率とIoUの予測値を掛け合わせたものをboxの評価値とする。

$$p_i^\text{box} = p_i^{\text{IoU}} \cdot p_i^\text{class}$$

ところが、クラス予測確率とIoU予測値は学習時は独立して学習しているのに対し、推論時に両者を掛け合わせているので、このようにヒューリスティックに決定したboxの評価値が真の評価値の推定値として最適である保証はない。
また、IoU予測値は正例のサンプルのみで学習しているため、負例に対しては過大なスコアを出力する可能性がある。

以上の考察に基づき、[2]ではクラス予測値とIoUスコアの予測値を同時に学習する手法を提案する。
具体的にはクラスの予測ヘッダを学習するさい、ターゲットをクラスのone-hotベクトルにGTとのIoUを掛け合わせたソフトラベルを用いる。

$$y_\text{soft} := \begin{cases} \text{IoU}(g_i, b_j) \cdot y, & y=1 \\ 0, & y=0 \end{cases}$$

なお、負例についてはIoUが定義できないため$\text{IoU}=0$とする。

また、RetinaNet以降に提案されたモデルは正例と負例のクラス不均衡を改善するために、Focal Lossを損失関数とする場合が多い。

$$\text{FL} := \begin{cases} - (1 - p)^{\gamma} \log(p), & y = 1 \\ - p^{\gamma} \log(1 - p), & y = 0 \end{cases}$$

ところが、Focal Lossはソフトラベルに対応していないので、[2]では以下のようなFocal lossをソフトラベルに拡張した損失関数を提案する。

$$\text{QFL} := - |y - p|^{\gamma} [y \log(p) + (1 - y) \log(1 - p)]$$

新しいloss関数ではBinary Cross Entropy LossにIoU評価値とclass-box評価値の誤差の$\beta$乗を重みづけしたものとなっている。これにより誤差が大きな難しいサンプルの効果を強調する役割を果たしている。

Focal Lossをソフトラベルに拡張したLossには他にもVFL(Varifocal Loss)[4]がある。

$$\text{VFL} := \begin{cases} - y [ y\log(p) + (1 - y) \log(1 - p) ], & y > 0 \\ - \alpha p^{\gamma} \log(1 - p), & y = 0 \end{cases}$$

こちらの形式では正例と負例で重みが非対称になっている。
負例に対しては元のFocal Lossと同じだが、正例に対してはソフトラベルとの誤差でなく、ソフトラベルの値自体を重みとして用いている。これは、著者らによると、「質の高い(=IoUの大きい)正例をより重視する」意図らしい。

論文中の報告では、QFL, VFLともにCOCO APで0.7-0.9ポイントのゲインを得ている[3,4]。

class予測タスクとbox回帰タスクをアーキテクチャレベルで協調して学習する

QFLやVFLではソフトラベルによって間接的にlocalityの評価値をclassification headに組み込んだが、依然として学習時はclassification taskとlocationの回帰タスクで独立したheadを使い学習している。

これに対し、TOOD[6]はさらに踏み込んでクラスの予測タスクとlocationの回帰タスクをアーキテクチャレベルで協調して学習する手法を提案した。

この研究ではclassの評価値が最大となるanchor boxとlocalityの評価値が最大となるanchor boxが異なることに着目し、両者に相関を持たせることを目標とする。

ナイーブには両者のheadの大部分を共通とし、最後の浅いレイヤのみ異なるアーキテクチャが考えうるが、一般的にクラスの予測とboxのlocationの回帰には特徴マップの同じ領域を使用するとは限らない。
これに対し、提案手法では特徴抽出用のheadの大部分は共通としつつ、タスクに応じて注目するfeature mapの領域を選択する方式をとる。

具体的には、以下のような処理を行う。

$$\begin{align*} X_1 &:= X^\text{FPN} \\ X_{k+1} &:= f_k(X_k) \\ X &:= \text{concat}([X_1, ..., X_N])\\ x &:= \text{AvgPool}(X) \\ w^\text{task} &:= \sigma(g^\text{task}(x)) \\ X_k^\text{task} &:= w^\text{task} \odot X_k \\ X^\text{task} &:= \text{concat}([X_1^\text{task}, ..., X_N^\text{task}]) \\ Z^\text{task} &:= h^\text{task}(X^\text{task}) \\ P^\text{align} &:= \sqrt{M \odot \sigma(Z^\text{class})} \\ B^\text{align} &:= Z^\text{box}(i + \Delta i, j + \Delta j) \\ M &:= \sigma(r_1(X)) \\ \Delta i &:= \sigma(r_2(X)) \\ \Delta j &:= \sigma(r_3(X)) \\ \end{align*}$$

表記について、$\sigma$はシグモイド関数を表わす。$f, g, h, r$は convolutionとactivation関数からなるマッピング関数である。$\odot$ は要素ごとの積を表す。$[\cdot]^\text{task}$の添字がついている部分はclass headとlocation registration headでそれぞれ独立したパラメータを持つ。

FPNの出力特徴マップから新たに抽出した特徴マップ$X_{k} (k=1, ..., N)$をclassificationとbox回帰タスクで共通とする。タスクごとに異なる部分はi) $X_k \rightarrow X_k^\text{task}$のマッピングの部分と、ii) $X_k^\text{task} \rightarrow Z_k^\text{task}$のマッピング、iii) $Z^\text{task} \rightarrow P^\text{align}, B^\text{align}$へのマッピングの部分である。i) はSqueeze and Excitation[9] モジュールで、global poolingによって空間方向の特徴を均質化し、チャネル方向の特徴選択に特化している。一方でiii) ではチャネル方向の特徴を均質化し、空間方向に特化した特徴選択を行う。特徴選択に用いられるテンソル$M, \Delta i, \Delta j$は、タスクに応じて異なる変調を加える。すなわち、クラス予測確率には特徴マップに空間方向の確率の重み$M$をモデル化するのに対し、boxのパラメータ回帰には、回帰の元となる特徴マップの $(x, y)$ 方向のずれ $(\Delta i, \Delta j)$ をモデル化する。後者のインデックスのシフト処理には、Deformable convolution[12]を用いてGPUを利用した並列計算を実現している。

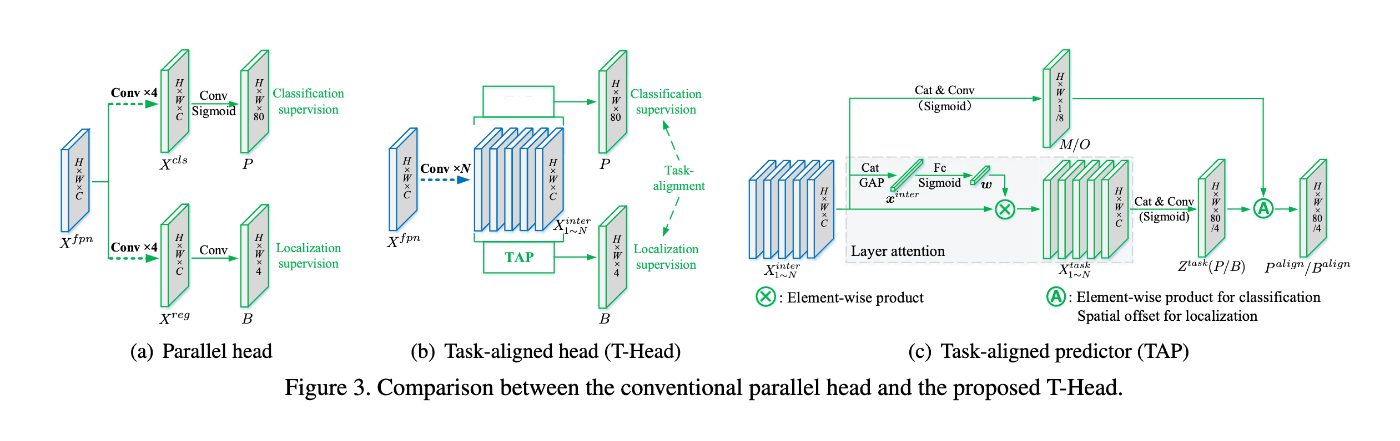
図. TOODのアーキテクチャ。[6]より抜粋。

headのアーキテクチャ変更に加え、boxの評価値をlossの重みづけとして用いる。boxの評価値は以下のようなヒューリスティックで決定する。

$$t_i = (p_i^\text{align})^\alpha \cdot \text{IoU}(b_i, g_j)^\beta$$

実際に使用する評価メトリクスは以下のように正規化している（論文によれば、$\alpha, \beta$が大きい場合に正例の評価値が小さくなり、学習が収束しなくなる問題に対応したらしい）。

$$\hat{t}_i = \frac{t_i}{\max_i ({t_i}) + \epsilon} \cdot \max_i{(\text{IoU}(b_i, g_j))}$$

損失関数は以下のようになる。

$$\begin{align*} \mathcal{L}(\hat{t}_i, \bar{b}_i, p_i, b_i) &= \mathcal{L}_\text{class} + \lambda \mathcal{L}_\text{reg} \\ \mathcal{L}_\text{class}(p_i, \hat{t}_i) &= \sum_{i \in \text{pos} + \text{neg}}\text{QFL}(p_i, \hat{t}_i) \\ \mathcal{L}_\text{reg}(b_i, \bar{b}_i, \hat{t}_i) &= \sum_{i \in \text{pos}} \hat{t}_i \text{GIoU}(b_i, \bar{b}_i) \end{align*}$$

classの回帰にQFLを用いているほか、boxのlocalityの回帰にboxの評価値によって重みづけを加えている（著者らによれば、このようにすることで質の高いboxの影響を大きくすることを意図したらしい）。

なお、QFLの論文ではNMSにおけるboxの評価値を最適化することが目標だったが、TOODではlabel assignmentでのboxの評価値を最適化することに用いている。

論文中のCOCO APによる評価結果では、QFL単体で0.9, headのアーキテクチャ変更で1.9、両者を共に用いることで2.3のゲインが得られたと報告している。

実用的なモデルにおけるdynamic label assignmentの採用実績について

本節では実用よりのモデルにおけるdynamic label assignmentの採用実績について説明する。「実用的」かどうかの基準は主観的にはなるが、大まかな区分けとしては、特定の要素技術の効果を明らかにするための研究用のモデルというよりは、最新の研究成果を積極的に取り込んだ、down-stream taskでの利用を前提としたモデルを想定している（例えば、ultralytics/ultralytics [10]など）。

YOLOX[5]では、OTA[3]を擬似的に再現したより計算機コストの小さいSimOTAと呼ばれるアルゴリズムによってOTAと同等の結果を得ることができたと報告している。SimOTAでは最適輸送問題を扱わずに、GT $g_i$ に対する予測box $p_j$ のclass評価とbox評価のlossを評価値 $C_{ij}$ としてGT近傍のtop-kの予測 boxおよびそれに所属するanchor boxを正例に割り当てる。

$$c_{ij} = L_{ij}^{\text{cls}} + \lambda L_{ij}^{\text{reg}}$$

また、RTMDet[8]ではYOLOXのSimOTAアルゴリズムにGTと予測boxの中心点同士の距離を推定したcenterness評価値を合わせたloss関数を用いている。

$$c_{ij} = L_{ij}^{\text{cls}} + \lambda_1 L_{ij}^{\text{reg}} + \lambda_2 L_{ij}^{\text{center}}$$

PP-YOLOE[11]およびYOLOv8[10]では、TOODで使われたTAL[6]において、QFLをVFLとDFL[2]に置き換えたlossを用いている。

$$\text{TAL}(b_i, \hat{t}_i, \bar{b_i}) = \frac{\sum_{i \in \text{pos + neg}} \text{VFL}(p_i, \hat{t_i}) + \lambda_1 \sum_{i \in \text{pos}} \text{GIoU}(b_i, \bar{b_i}) + \lambda_2 \sum_{i \in \text{pos}} \text{DFL}(b_i, \bar{b_i})}{\sum_{i \in \text{pos}} \hat{t}_i}$$

DFLはboxの回帰において確率モデルを導入した損失である。モデルはboxの位置情報(top, left, right, bottom)のそれぞれについての確率分布$S_k (k \in [0, 1, ..., N-1])$をパラメータとして持つが、空間上の全ての点について期待値を計算すると、同じ期待値をとる確率分布が複数存在するために、学習の収束が遅くなることが懸念される。このため、正解ラベルの前後の2点 $y_i, y_{i+1}, y \in [y_i, y_{i+1})$ の対数確率を線形補完したものをlossとする。これは「想定する確率分布は正解ラベルの近くで大きな値をとる」という事前知識を反映したものである。したがって、DFLは以下のように定義される。

$$\text{DFL}(S_k, S_{k+1}, y) := -((y_{k+1} - y)\log(S_k) + (y - y_k) \log(S_{k+1}))$$

まとめ

本稿では、object detectionタスクにおけるlabel assignment関連の最近（2019年以降）の研究成果について、以下の内容を説明した。

1. anchor boxとprediction boxを共にlabel assignmentで利用する手法[7]
2. class予測の評価値とlocalityの評価値を組み合わせたboxの評価手法、およびそれをpostprocessやlabel assignmentに利用する手法
   1. IoU評価値をclass予測タスクのソフトラベルとして用いる[2, 4, 6]
   2. class予測タスクとbox回帰タスクをアーキテクチャレベルで協調して学習する[6]
3. 実用的なモデルにおけるdynamic assignment手法の採用実績について[5, 8, 10, 11]

Reference

• [1] Bridging the Gap Between Anchor-based and Anchor-free Detection via Adaptive Training Sample Selection, Jun 2020
• [2] Generalized Focal Loss: Learning Qualified and Distributed Bounding Boxes for Dense Object Detection, Jun 2020
• [3] OTA: Optimal Transport Assignment for Object Detection, Mar 2021
• [4] VarifocalNet: An IoU-aware Dense Object Detector, Mar 2021
• [5] YOLOX: Exceeding YOLO Series in 2021, Aug 2021
• [6] TOOD: Task-aligned One-stage Object Detection, Aug 2021
• [7] Dynamic Label Assignment for Object Detection by Combining Predicted IoUs and Anchor IoUs, Jul 2022
• [8] RTMDet: An Empirical Study of Designing Real-Time Object Detectors, Dec 2022
• [9] Squeeze-and-Excitation Networks, May 2019
• [10] https://github.com/ultralytics/ultralytics
• [11] PP-YOLOE: An evolved version of YOLO, Mar 2022
• [12] Deformable Convolutional Networks, Jun 2017