Python データ構造チートシート(完全版)
🧠 はじめに
データ構造を理解することは、アルゴリズムの武器を扱う練習。
ここでは主要な構造の「使いどころ」+「操作」+「Big O」+「for ループ/再帰例」を網羅します。
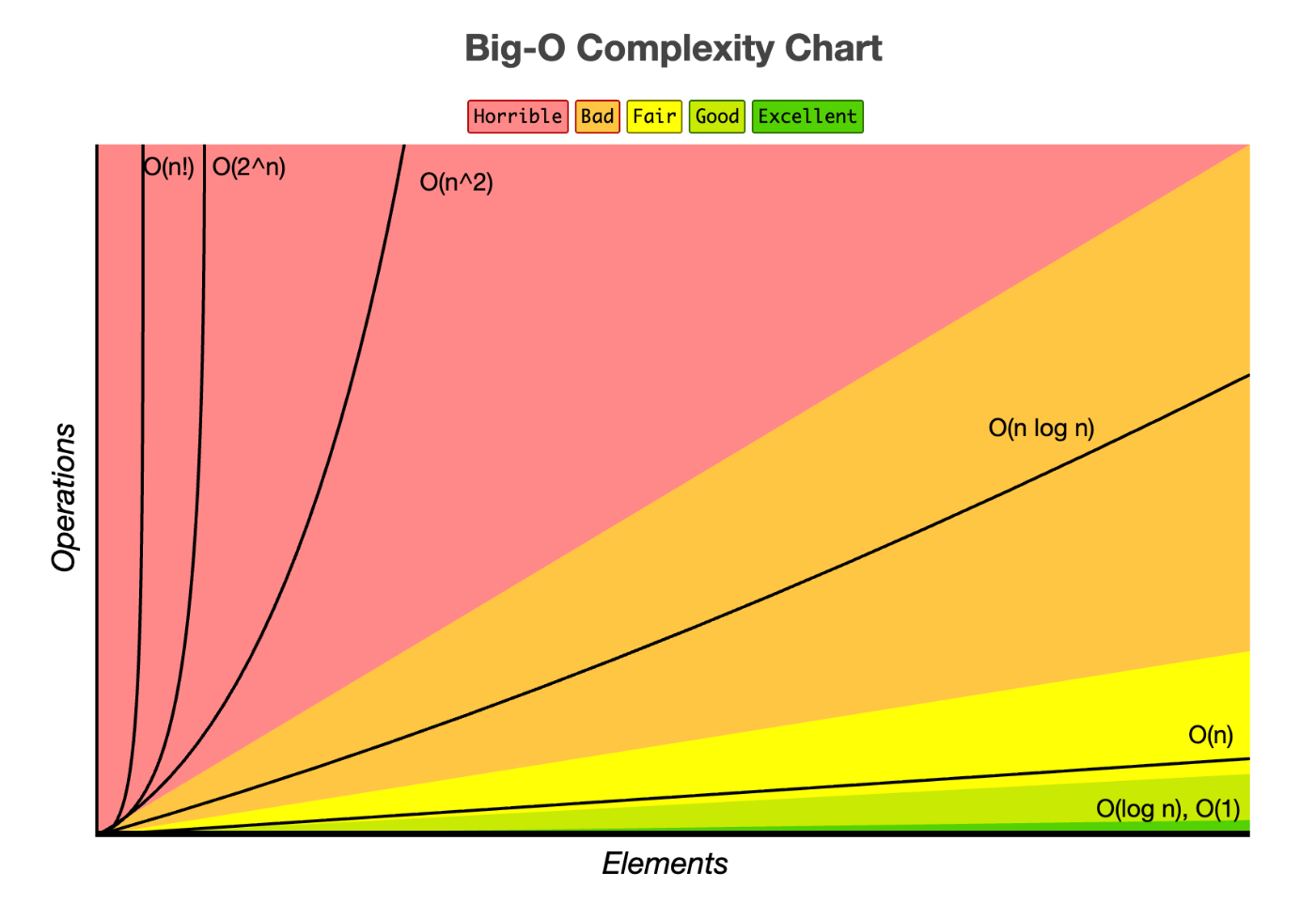

🧩 List(リスト)
概要
順序を持つ配列。append・pop・sort が主な操作。
インデックスアクセスが O(1)。
どんなときに使うか?
- 順序付きデータの管理
- スタック・キューの実装
- 配列ベースのアルゴリズム
- 動的サイズの配列が必要な場合
メリット・デメリット
メリット:
- インデックスアクセスが O(1)
- 末尾への追加が O(1)
- スライシングが簡単
- 豊富な組み込みメソッド
デメリット:
- 先頭への挿入が O(n)
- 検索が O(n)
- メモリが連続的である必要がある
操作
要素にアクセス
li = ['apple', 'banana', 'grape']
print(li[0]) # apple
print(li[-1]) # grape(末尾から)
Big O: O(1)
➕ 末尾に追加
li = []
li.append(1)
li.append(2)
# または
li += [3, 4] # 複数要素を一度に追加
Big O: O(1)
➕ 先頭に挿入
li.insert(0, 5) # 位置0に挿入
Big O: O(n)
➕ 任意の位置に挿入
li = [1, 2, 3, 4]
li.insert(2, 99) # 位置2に99を挿入
# 結果: [1, 2, 99, 3, 4]
Big O: O(n)
➖ 末尾削除
li.pop() # 末尾を削除して返す
li.pop(0) # 先頭を削除(O(n))
Big O: O(1) - 末尾、O(n) - 先頭
➖ 値で削除
li = [1, 2, 3, 2]
li.remove(2) # 最初の2を削除
# 結果: [1, 3, 2]
Big O: O(n)
🔍 検索
li = ['apple', 'banana', 'grape']
if 'apple' in li:
print("存在する")
# インデックスを取得
index = li.index('banana') # 1
Big O: O(n)
✂️ スライシング
li = [0, 1, 2, 3, 4, 5]
li[1:4] # [1, 2, 3]
li[:3] # [0, 1, 2]
li[2:] # [2, 3, 4, 5]
li[::2] # [0, 2, 4](2つ飛ばし)
li[::-1] # [5, 4, 3, 2, 1, 0](逆順)
Big O: O(k) - k はスライスの長さ
- Python のスライス "s[a:b]" は新しい文字列をゼロからコピーします。
- つまり部分文字列の長さだけループが回る。
🔁 ソート
li = [3, 1, 4, 1, 5]
li.sort() # 破壊的: [1, 1, 3, 4, 5]
sorted_li = sorted(li) # 非破壊的
# 降順
li.sort(reverse=True)
# カスタムキー
li.sort(key=lambda x: x % 3)
Big O: O(n log n)
🔄 反転
li = [1, 2, 3]
li.reverse() # 破壊的: [3, 2, 1]
reversed_li = li[::-1] # 非破壊的
Big O: O(n)
📏 長さ・最大・最小
li = [1, 5, 3, 9, 2]
len(li) # 5
max(li) # 9
min(li) # 1
sum(li) # 20
Big O: O(n)
📝 リスト内包表記
# 基本的な内包表記
squares = [x**2 for x in range(10)]
# [0, 1, 4, 9, 16, 25, 36, 49, 64, 81]
# 条件付き
evens = [x for x in range(10) if x % 2 == 0]
# [0, 2, 4, 6, 8]
# ネスト
matrix = [[i*j for j in range(3)] for i in range(3)]
# [[0, 0, 0], [0, 1, 2], [0, 2, 4]]
🌀 Iterable(for ループ)例
for x in li:
print(x)
🔁 再帰(Recursion)例
def print_list(li, i=0):
if i == len(li): return
print(li[i])
print_list(li, i + 1)
print_list([1,2,3])
💡 実用例:スタック・キュー
# スタック(LIFO)
stack = []
stack.append(1) # push
stack.append(2)
top = stack.pop() # pop: 2
# キュー(FIFO)- 効率悪い(O(n))
queue = []
queue.append(1) # enqueue
queue.append(2)
first = queue.pop(0) # dequeue: 1(O(n))
# 効率的なキューは deque を使用
💡 実用例:2 つのポインタ
def two_sum_sorted(nums, target):
"""ソート済み配列で2つの和を探す"""
left, right = 0, len(nums) - 1
while left < right:
current_sum = nums[left] + nums[right]
if current_sum == target:
return [left, right]
elif current_sum < target:
left += 1
else:
right -= 1
return []
🧭 Hash Map(辞書 / dict)
概要
キーと値のペアを O(1)で扱えるハッシュ構造。
Python 3.7+ では挿入順序を保持。
どんなときに使うか?
- 高速な検索・更新が必要な場合
- 頻度カウント・グループ化
- キャッシュ・マッピング
- グラフの隣接リスト表現
メリット・デメリット
メリット:
- 検索・挿入・削除が平均 O(1)
- キーと値の柔軟なマッピング
- 豊富な操作メソッド
デメリット:
- 最悪ケースで O(n)(ハッシュ衝突)
- メモリ使用量が大きい
- キーはハッシュ可能でなければならない
操作
➕ 追加 / 更新
d = {}
d["apple"] = 5
d["banana"] = 3
d["apple"] = 10 # 更新
# 複数要素を一度に
d.update({"grape": 7, "orange": 2})
Big O: O(1)
🔍 検索
d = {"apple": 2, "banana": 4}
# 存在確認
if "apple" in d:
print(d["apple"]) # 2
# 安全に取得(キーがない場合のデフォルト値)
value = d.get("apple", 0) # 2
value = d.get("mango", 0) # 0(キーがない場合)
Big O: O(1)
➖ 削除
del d["apple"]
# または
d.pop("apple") # 値を返す
d.pop("mango", None) # キーがない場合のデフォルト値
Big O: O(1)
📊 頻度カウント
from collections import Counter
# 方法1: Counter を使用
nums = [1, 2, 2, 3, 3, 3]
counter = Counter(nums)
# Counter({3: 3, 2: 2, 1: 1})
# 方法2: 手動でカウント
count = {}
for num in nums:
count[num] = count.get(num, 0) + 1
Big O: O(n)
🔄 デフォルト値付き辞書
from collections import defaultdict
# デフォルト値が自動的に設定される
dd = defaultdict(int)
dd["apple"] += 1 # 0から開始
dd["banana"] += 1
# リストをデフォルト値に
dd_list = defaultdict(list)
dd_list["fruits"].append("apple")
📝 辞書内包表記
# 基本的な内包表記
squares = {x: x**2 for x in range(5)}
# {0: 0, 1: 1, 2: 4, 3: 9, 4: 16}
# 条件付き
evens = {x: x*2 for x in range(10) if x % 2 == 0}
# 既存の辞書から変換
original = {"a": 1, "b": 2, "c": 3}
doubled = {k: v*2 for k, v in original.items()}
🔑 キー・値・アイテムの取得
d = {"apple": 5, "banana": 3}
keys = d.keys() # dict_keys(['apple', 'banana'])
values = d.values() # dict_values([5, 3])
items = d.items() # dict_items([('apple', 5), ('banana', 3)])
# リストに変換
list(d.keys()) # ['apple', 'banana']
🌀 Iterable(for ループ)例
for k, v in d.items():
print(k, v)
🔁 再帰(Recursion)例
辞書は通常再帰しないが、ネスト辞書の探索で使える。
def traverse_dict(d):
for k, v in d.items():
if isinstance(v, dict):
traverse_dict(v)
else:
print(k, v)
💡 実用例:2 つの和(Two Sum)
def two_sum(nums, target):
"""O(n)で2つの和を探す"""
seen = {}
for i, num in enumerate(nums):
complement = target - num
if complement in seen:
return [seen[complement], i]
seen[num] = i
return []
💡 実用例:グループ化
from collections import defaultdict
def group_by_key(items, key_func):
"""キー関数でグループ化"""
groups = defaultdict(list)
for item in items:
key = key_func(item)
groups[key].append(item)
return dict(groups)
# 使用例
students = [
{"name": "Alice", "grade": "A"},
{"name": "Bob", "grade": "B"},
{"name": "Charlie", "grade": "A"}
]
grouped = group_by_key(students, lambda x: x["grade"])
# {'A': [{'name': 'Alice', ...}, ...], 'B': [...]}
🔁 Deque(両端キュー)
概要
両端の追加・削除が O(1)。collections.dequeを利用。
リストの先頭操作が O(n) なのに対し、deque は O(1)。
どんなときに使うか?
- BFS(幅優先探索)/ キュー実装
- スライディングウィンドウ
- パリンドローム判定
- 両端操作が頻繁な場合
メリット・デメリット
メリット:
- 両端の操作が O(1)
- メモリ効率が良い
- スレッドセーフな操作
デメリット:
- 中間要素へのアクセスが O(n)
- リストより機能が限定的
操作
➕ 両端操作
from collections import deque
dq = deque()
# 右端(末尾)に追加
dq.append(1)
dq.append(2)
# 左端(先頭)に追加
dq.appendleft(0)
# 右端から削除
dq.pop() # 2
# 左端から削除
dq.popleft() # 0
Big O: O(1)
🔄 回転
dq = deque([1, 2, 3, 4, 5])
dq.rotate(2) # 右に2回転: [4, 5, 1, 2, 3]
dq.rotate(-1) # 左に1回転: [5, 1, 2, 3, 4]
Big O: O(k) - k は回転数
📏 長さ・最大長
dq = deque([1, 2, 3], maxlen=5)
len(dq) # 3
dq.maxlen # 5(設定した場合)
# 最大長を設定すると、追加時に自動で削除
dq = deque([1, 2, 3], maxlen=3)
dq.append(4) # [2, 3, 4](先頭が自動削除)
🔍 インデックスアクセス
dq = deque([1, 2, 3, 4, 5])
dq[0] # 1(先頭)
dq[-1] # 5(末尾)
dq[2] # 3(中間、O(n))
Big O: O(1) - 両端、O(n) - 中間
🌀 Iterable
for x in dq:
print(x)
🔁 再帰(キュー処理例)
def process(dq):
if not dq:
return
x = dq.popleft()
print(x)
process(dq)
💡 実用例:BFS(幅優先探索)
from collections import deque
def bfs(graph, start):
"""グラフのBFS"""
queue = deque([start])
visited = {start}
while queue:
node = queue.popleft()
print(node)
for neighbor in graph[node]:
if neighbor not in visited:
visited.add(neighbor)
queue.append(neighbor)
💡 実用例:スライディングウィンドウ最大値
from collections import deque
def max_sliding_window(nums, k):
"""サイズkのスライディングウィンドウの最大値"""
dq = deque() # インデックスを保存
result = []
for i, num in enumerate(nums):
# 範囲外のインデックスを削除
while dq and dq[0] <= i - k:
dq.popleft()
# 現在の値より小さい要素を削除
while dq and nums[dq[-1]] < num:
dq.pop()
dq.append(i)
# ウィンドウサイズに達したら結果に追加
if i >= k - 1:
result.append(nums[dq[0]])
return result
💡 実用例:パリンドローム判定
from collections import deque
def is_palindrome(s):
"""両端から比較してパリンドローム判定"""
dq = deque(s.lower().replace(" ", ""))
while len(dq) > 1:
if dq.popleft() != dq.pop():
return False
return True
🌿 Set(集合)
概要
重複なし、順序なし(Python 3.7+ では挿入順序を保持)。
探索・追加・削除が平均 O(1)。
どんなときに使うか?
- 重複排除
- 存在判定を高速化
- 集合演算(和・積・差)
- グラフの訪問済みノード管理
メリット・デメリット
メリット:
- 検索・挿入・削除が平均 O(1)
- 重複を自動で排除
- 集合演算が簡単
デメリット:
- 順序が保証されない(Python 3.7+ は例外)
- ハッシュ可能な要素のみ
- メモリ使用量が大きい
操作
➕ 追加
s = set()
s.add(1)
s.add(2)
s.add(1) # 重複は無視
# {1, 2}
# 複数要素を一度に
s.update([3, 4, 5])
Big O: O(1)
🔍 存在確認
s = {1, 2, 3}
1 in s # True
4 in s # False
Big O: O(1)
➖ 削除
s = {1, 2, 3}
s.remove(2) # キーがないとエラー
s.discard(4) # キーがなくてもエラーにならない
s.pop() # 任意の要素を削除して返す
Big O: O(1)
🔄 集合演算
a = {1, 2, 3, 4}
b = {3, 4, 5, 6}
# 和集合(union)
a | b # {1, 2, 3, 4, 5, 6}
a.union(b)
# 積集合(intersection)
a & b # {3, 4}
a.intersection(b)
# 差集合(difference)
a - b # {1, 2}
a.difference(b)
# 対称差(symmetric difference)
a ^ b # {1, 2, 5, 6}
a.symmetric_difference(b)
# 部分集合判定
{1, 2}.issubset(a) # True
a.issuperset({1, 2}) # True
Big O: O(len(a) + len(b))
文字列をset
set(string)
Big O: O(W)
- window_string の各文字を set に挿入
- set.insert は平均 O(1)
- W 個の文字を挿入する → 合計 O(W)
📝 集合内包表記
# 基本的な内包表記
squares = {x**2 for x in range(5)}
# {0, 1, 4, 9, 16}
# 条件付き
evens = {x for x in range(10) if x % 2 == 0}
# {0, 2, 4, 6, 8}
🌀 Iterable
for val in s:
print(val)
🔁 再帰(例:集合を消費しながら出力)
def print_set(s):
if not s: return
val = s.pop()
print(val)
print_set(s)
💡 実用例:重複排除
def remove_duplicates(nums):
"""リストから重複を削除(順序保持)"""
seen = set()
result = []
for num in nums:
if num not in seen:
seen.add(num)
result.append(num)
return result
# または(Python 3.7+)
list(dict.fromkeys(nums))
💡 実用例:2 つの配列の共通要素
def find_common(nums1, nums2):
"""2つの配列の共通要素を探す"""
set1 = set(nums1)
set2 = set(nums2)
return list(set1 & set2) # 積集合
💡 実用例:サイクル検出
def has_duplicate(nums):
"""リストに重複があるか判定"""
return len(nums) != len(set(nums))
🪜 Heap(ヒープ / heapq)
概要
最小値を O(1)で取得、挿入削除は O(log n)。
Python の heapq は最小ヒープ(min-heap)を実装。
どんなときに使うか?
- 優先度付きキュー
- K 最小 / K 最大問題
- マージ K 個のソート済みリスト
- ダイクストラ法
メリット・デメリット
メリット:
- 最小値取得が O(1)
- 挿入・削除が O(log n)
- メモリ効率が良い
デメリット:
- 最大値取得は O(n) または O(log n)(工夫が必要)
- 中間要素へのアクセスが困難
- ソート済みではない
操作
➕ 挿入
import heapq
h = []
heapq.heappush(h, 3)
heapq.heappush(h, 1)
heapq.heappush(h, 2)
# h = [1, 3, 2](最小値が先頭)
Big O: O(log n)
➖ 最小値を取得・削除
x = heapq.heappop(h) # 1(最小値)
# h = [2, 3]
Big O: O(log n)
👁️ 最小値を取得(削除しない)
min_val = h[0] # 最小値を取得(削除しない)
Big O: O(1)
🔄 リストをヒープ化
nums = [3, 1, 4, 1, 5]
heapq.heapify(nums) # インプレースでヒープ化
# nums = [1, 1, 4, 3, 5]
Big O: O(n)
📊 最大ヒープの実装
# 最大ヒープは負の値を使う
max_heap = []
heapq.heappush(max_heap, -3)
heapq.heappush(max_heap, -1)
heapq.heappush(max_heap, -2)
max_val = -heapq.heappop(max_heap) # 3(最大値)
🎯 カスタム比較(タプルを使用)
# タプルの最初の要素で比較
heap = []
heapq.heappush(heap, (3, "task3"))
heapq.heappush(heap, (1, "task1"))
heapq.heappush(heap, (2, "task2"))
priority, task = heapq.heappop(heap) # (1, "task1")
🔍 n 個の最大/最小要素
import heapq
nums = [1, 8, 2, 23, 7, -4, 18, 23, 42, 37, 2]
# 3つの最小値
smallest = heapq.nsmallest(3, nums) # [-4, 1, 2]
# 3つの最大値
largest = heapq.nlargest(3, nums) # [42, 37, 23]
Big O: O(n log k) - k は取得する要素数
🌀 Iterable
ヒープは常に「最小値が先頭」にある。
while h:
print(heapq.heappop(h))
🔁 再帰
def print_heap(h):
if not h: return
print(heapq.heappop(h))
print_heap(h)
💡 実用例:K 個の最大要素
import heapq
def find_k_largest(nums, k):
"""K個の最大要素を取得"""
# 最小ヒープでサイズkを維持
min_heap = []
for num in nums:
heapq.heappush(min_heap, num)
if len(min_heap) > k:
heapq.heappop(min_heap) # 最小値を削除
return min_heap
💡 実用例:マージ K 個のソート済みリスト
import heapq
def merge_k_sorted(lists):
"""K個のソート済みリストをマージ"""
heap = []
# 各リストの最初の要素をヒープに追加
for i, lst in enumerate(lists):
if lst:
heapq.heappush(heap, (lst[0], i, 0))
result = []
while heap:
val, list_idx, elem_idx = heapq.heappop(heap)
result.append(val)
# 同じリストの次の要素を追加
if elem_idx + 1 < len(lists[list_idx]):
next_val = lists[list_idx][elem_idx + 1]
heapq.heappush(heap, (next_val, list_idx, elem_idx + 1))
return result
💡 実用例:優先度付きキュー
import heapq
class PriorityQueue:
def __init__(self):
self.heap = []
def push(self, priority, item):
heapq.heappush(self.heap, (priority, item))
def pop(self):
return heapq.heappop(self.heap)[1]
def is_empty(self):
return len(self.heap) == 0
# 使用例
pq = PriorityQueue()
pq.push(3, "低優先度タスク")
pq.push(1, "高優先度タスク")
pq.push(2, "中優先度タスク")
while not pq.is_empty():
print(pq.pop()) # 高優先度から順に
🔗 Linked List(単方向)
概要
1 つのノードが「次」を指す線形データ構造。
各ノードは値と次のノードへの参照を持つ。
どんなときに使うか?
- 動的なサイズ変更が必要な場合
- 先頭への挿入・削除が頻繁な場合
- メモリが不連続でも良い場合
- スタック・キューの実装
メリット・デメリット
メリット:
- 先頭への挿入・削除が O(1)
- 動的なサイズ変更が容易
- メモリを効率的に使用
デメリット:
- ランダムアクセスができない(O(n))
- 末尾への挿入が O(n)
- 各ノードにポインタ分のメモリオーバーヘッド
実装
class Node:
def __init__(self, val):
self.val = val
self.next = None
より実用的なクラス実装:
class LinkedList:
def __init__(self):
self.head = None
def append(self, val):
"""末尾に追加"""
if not self.head:
self.head = Node(val)
return
cur = self.head
while cur.next:
cur = cur.next
cur.next = Node(val)
def prepend(self, val):
"""先頭に追加"""
new_node = Node(val)
new_node.next = self.head
self.head = new_node
操作
➕ 先頭に挿入
def insert_at_head(head, val):
new_node = Node(val)
new_node.next = head
return new_node # 新しいheadを返す
# 使用例
head = Node(1)
head = insert_at_head(head, 0) # 0 -> 1
Big O: O(1)
➕ 途中に挿入(位置指定)
def insert_at_position(head, val, position):
if position == 0:
return insert_at_head(head, val)
new_node = Node(val)
cur = head
for _ in range(position - 1):
if cur is None:
raise IndexError("Position out of range")
cur = cur.next
new_node.next = cur.next
cur.next = new_node
return head
# 使用例: 1 -> 2 -> 3 の2番目(0-indexed)に5を挿入
# 結果: 1 -> 2 -> 5 -> 3
Big O: O(n) - 位置まで辿る必要がある
➕ 末尾に挿入
def insert_at_tail(head, val):
new_node = Node(val)
if head is None:
return new_node
cur = head
while cur.next:
cur = cur.next
cur.next = new_node
return head
# 使用例
head = Node(1)
head = insert_at_tail(head, 2) # 1 -> 2
head = insert_at_tail(head, 3) # 1 -> 2 -> 3
Big O: O(n) - 末尾まで辿る必要がある
➖ 先頭を削除
def delete_at_head(head):
if head is None:
return None
return head.next # 次のノードを新しいheadに
# 使用例: 1 -> 2 -> 3 から先頭を削除
# 結果: 2 -> 3
Big O: O(1)
➖ 途中を削除(位置指定)
def delete_at_position(head, position):
if head is None:
return None
if position == 0:
return head.next
cur = head
for _ in range(position - 1):
if cur is None or cur.next is None:
raise IndexError("Position out of range")
cur = cur.next
cur.next = cur.next.next
return head
# 使用例: 1 -> 2 -> 3 の1番目(0-indexed)を削除
# 結果: 1 -> 3
Big O: O(n) - 位置まで辿る必要がある
➖ 末尾を削除
def delete_at_tail(head):
if head is None or head.next is None:
return None
cur = head
while cur.next.next:
cur = cur.next
cur.next = None
return head
# 使用例: 1 -> 2 -> 3 から末尾を削除
# 結果: 1 -> 2
Big O: O(n) - 末尾の 1 つ前まで辿る必要がある
🔍 値で検索
def search_by_value(head, val):
cur = head
while cur:
if cur.val == val:
return cur
cur = cur.next
return None
# 使用例
node = search_by_value(head, 2) # 値が2のノードを返す
Big O: O(n)
➖ 値で削除
def delete_by_value(head, val):
if head is None:
return None
if head.val == val:
return head.next
cur = head
while cur.next:
if cur.next.val == val:
cur.next = cur.next.next
return head
cur = cur.next
return head
# 使用例: 1 -> 2 -> 3 から値2を削除
# 結果: 1 -> 3
Big O: O(n)
📏 長さを取得
def get_length(head):
length = 0
cur = head
while cur:
length += 1
cur = cur.next
return length
# 再帰版
def get_length_recursive(head):
if head is None:
return 0
return 1 + get_length_recursive(head.next)
Big O: O(n)
🔄 リストを反転
def reverse_list(head):
prev = None
cur = head
while cur:
next_node = cur.next
cur.next = prev
prev = cur
cur = next_node
return prev
# 使用例: 1 -> 2 -> 3 を反転
# 結果: 3 -> 2 -> 1
Big O: O(n)
🔁 再帰で反転
def reverse_list_recursive(head):
if head is None or head.next is None:
return head
new_head = reverse_list_recursive(head.next)
head.next.next = head
head.next = None
return new_head
Big O: O(n)
🔍 サイクル検出(Floyd's Cycle Detection)
def has_cycle(head):
"""スローファストポインタでサイクルを検出"""
if not head or not head.next:
return False
slow = head
fast = head.next
while fast and fast.next:
if slow == fast:
return True
slow = slow.next
fast = fast.next.next
return False
# 使用例
# 1 -> 2 -> 3 -> 2 (サイクル)
# has_cycle(head) -> True
Big O: O(n) - 時間、O(1) - 空間
📍 中間ノードを取得
def get_middle(head):
"""スローファストポインタで中間を取得"""
if not head:
return None
slow = head
fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
return slow
# 使用例: 1 -> 2 -> 3 -> 4 -> 5
# 結果: 3
Big O: O(n)
🌀 Iterable
cur = head
while cur:
print(cur.val)
cur = cur.next
🔁 再帰
def print_linked(node):
if not node: return
print(node.val)
print_linked(node.next)
🔗 Linked List(双方向)
概要
前後のポインタを持つ線形データ構造。
各ノードは値と前後のノードへの参照を持つ。
どんなときに使うか?
- LRU キャッシュの実装
- 双方向ナビゲーションが必要な場合
- 既知のノードを O(1) で削除したい場合
- デック(両端キュー)の実装
メリット・デメリット
メリット:
- 既知のノードの削除が O(1)
- 前方向・後方向の両方から走査可能
- より柔軟な操作が可能
デメリット:
- メモリオーバーヘッドが大きい(2 つのポインタ)
- 実装が複雑
- 単方向より多くのメモリを使用
実装
class DNode:
def __init__(self, val):
self.val = val
self.prev = None
self.next = None
より実用的なクラス実装(ダミーノード使用):
class DoublyLinkedList:
def __init__(self):
# ダミーノードでエッジケースを簡略化
self.head = DNode(0) # ダミーヘッド
self.tail = DNode(0) # ダミーテール
self.head.next = self.tail
self.tail.prev = self.head
def append(self, val):
"""末尾に追加"""
new_node = DNode(val)
new_node.prev = self.tail.prev
new_node.next = self.tail
self.tail.prev.next = new_node
self.tail.prev = new_node
操作
➕ 先頭に挿入
def insert_at_head(head, val):
new_node = DNode(val)
if head is None:
return new_node
new_node.next = head
head.prev = new_node
return new_node # 新しいheadを返す
# 使用例
head = DNode(1)
head = insert_at_head(head, 0) # 0 <-> 1
Big O: O(1)
➕ 途中に挿入(位置指定)
def insert_at_position(head, val, position):
if position == 0:
return insert_at_head(head, val)
new_node = DNode(val)
cur = head
for _ in range(position - 1):
if cur is None:
raise IndexError("Position out of range")
cur = cur.next
if cur.next:
new_node.next = cur.next
cur.next.prev = new_node
new_node.prev = cur
cur.next = new_node
return head
# 使用例: 1 <-> 2 <-> 3 の2番目(0-indexed)に5を挿入
# 結果: 1 <-> 2 <-> 5 <-> 3
Big O: O(n) - 位置まで辿る必要がある
➕ 末尾に挿入
def insert_at_tail(head, val):
new_node = DNode(val)
if head is None:
return new_node
cur = head
while cur.next:
cur = cur.next
cur.next = new_node
new_node.prev = cur
return head
# 使用例
head = DNode(1)
head = insert_at_tail(head, 2) # 1 <-> 2
head = insert_at_tail(head, 3) # 1 <-> 2 <-> 3
Big O: O(n) - 末尾まで辿る必要がある
➖ 先頭を削除
def delete_at_head(head):
if head is None:
return None
if head.next is None:
return None
new_head = head.next
new_head.prev = None
return new_head
# 使用例: 1 <-> 2 <-> 3 から先頭を削除
# 結果: 2 <-> 3
Big O: O(1)
➖ 途中を削除(ノード指定)
def delete_node(node):
"""ノード自体を削除(双方向の強み)"""
if node.prev:
node.prev.next = node.next
if node.next:
node.next.prev = node.prev
# 使用例
# 1 <-> 2 <-> 3 で node2 を削除
delete_node(node2) # 結果: 1 <-> 3
Big O: O(1) - ノードが既に分かっている場合
➖ 途中を削除(位置指定)
def delete_at_position(head, position):
if head is None:
return None
if position == 0:
return delete_at_head(head)
cur = head
for _ in range(position):
if cur is None:
raise IndexError("Position out of range")
cur = cur.next
if cur.prev:
cur.prev.next = cur.next
if cur.next:
cur.next.prev = cur.prev
return head
# 使用例: 1 <-> 2 <-> 3 の1番目(0-indexed)を削除
# 結果: 1 <-> 3
Big O: O(n) - 位置まで辿る必要がある(削除自体は O(1))
➖ 末尾を削除
def delete_at_tail(head):
if head is None:
return None
if head.next is None:
return None
cur = head
while cur.next:
cur = cur.next
cur.prev.next = None
return head
# 使用例: 1 <-> 2 <-> 3 から末尾を削除
# 結果: 1 <-> 2
Big O: O(n) - 末尾まで辿る必要がある(削除自体は O(1))
🔍 値で検索
def search_by_value(head, val):
cur = head
while cur:
if cur.val == val:
return cur
cur = cur.next
return None
Big O: O(n)
➖ 値で削除
def delete_by_value(head, val):
cur = head
while cur:
if cur.val == val:
if cur.prev:
cur.prev.next = cur.next
else:
head = cur.next
if cur.next:
cur.next.prev = cur.prev
return head
cur = cur.next
return head
Big O: O(n) - 検索は O(n)、削除自体は O(1)
📏 長さを取得
def get_length(head):
length = 0
cur = head
while cur:
length += 1
cur = cur.next
return length
Big O: O(n)
🔄 リストを反転
def reverse_list(head):
if not head:
return None
cur = head
# 前後を入れ替えながら進む
while cur:
cur.prev, cur.next = cur.next, cur.prev
head = cur # 最後のノードが新しいhead
cur = cur.prev # 元のnext方向に進む
return head
Big O: O(n)
🔗 ノードを移動(LRU キャッシュで使用)
def move_to_head(head, node):
"""ノードを先頭に移動"""
if node.prev:
node.prev.next = node.next
if node.next:
node.next.prev = node.prev
node.next = head
node.prev = None
if head:
head.prev = node
return node
Big O: O(1)
🌀 Iterable(前方向)
cur = head
while cur:
print(cur.val)
cur = cur.next
🌀 Iterable(逆方向)
cur = tail
while cur:
print(cur.val)
cur = cur.prev
🔁 再帰(前方向)
def traverse(node):
if not node: return
print(node.val)
traverse(node.next)
🔁 再帰(逆方向)
def traverse_reverse(node):
if not node: return
print(node.val)
traverse_reverse(node.prev)
💡 実用例:LRU キャッシュ
class LRUCache:
def __init__(self, capacity):
self.capacity = capacity
self.cache = {}
self.head = DNode(0)
self.tail = DNode(0)
self.head.next = self.tail
self.tail.prev = self.head
def _add_node(self, node):
"""先頭に追加"""
node.prev = self.head
node.next = self.head.next
self.head.next.prev = node
self.head.next = node
def _remove_node(self, node):
"""ノードを削除"""
node.prev.next = node.next
node.next.prev = node.prev
def get(self, key):
if key in self.cache:
node = self.cache[key]
self._remove_node(node)
self._add_node(node)
return node.val
return -1
def put(self, key, value):
if key in self.cache:
node = self.cache[key]
node.val = value
self._remove_node(node)
self._add_node(node)
else:
if len(self.cache) >= self.capacity:
# 末尾(最も古い)を削除
lru = self.tail.prev
self._remove_node(lru)
del self.cache[lru.key]
new_node = DNode(value)
new_node.key = key
self.cache[key] = new_node
self._add_node(new_node)
🌐 Union-Find(素集合)
概要
グループを統合・判定するデータ構造。
互いに素な集合(Disjoint Set)を効率的に管理。
findとunionの 2 操作で、ほぼ定数時間(O(α(n)))で動作。
どんなときに使うか?
- グラフの連結成分判定
- 最小全域木(Kruskal 法)
- ネットワークの接続性判定
- グループ分け問題
メリット・デメリット
メリット:
- 経路圧縮とランク統合によりほぼ定数時間
- 実装が比較的簡単
- メモリ効率が良い
デメリット:
- 要素の削除が困難
- 動的な要素追加には工夫が必要
実装
基本的な実装(経路圧縮のみ)
class DSU:
def __init__(self, n):
self.p = list(range(n)) # 親配列
def find(self, x):
"""経路圧縮付きfind"""
if self.p[x] != x:
self.p[x] = self.find(self.p[x]) # 経路圧縮
return self.p[x]
def union(self, x, y):
"""2つのグループを統合"""
self.p[self.find(x)] = self.find(y)
改善版(経路圧縮 + ランク統合)
class DSU:
def __init__(self, n):
self.p = list(range(n))
self.rank = [0] * n # ランク(木の高さ)
def find(self, x):
"""経路圧縮付きfind"""
if self.p[x] != x:
self.p[x] = self.find(self.p[x])
return self.p[x]
def union(self, x, y):
"""ランク統合で効率化"""
px, py = self.find(x), self.find(y)
if px == py:
return # 既に同じグループ
# ランクの小さい方を大きい方に統合
if self.rank[px] < self.rank[py]:
self.p[px] = py
elif self.rank[px] > self.rank[py]:
self.p[py] = px
else:
self.p[py] = px
self.rank[px] += 1
def connected(self, x, y):
"""2つの要素が同じグループか判定"""
return self.find(x) == self.find(y)
Big O: O(α(n)) - α はアッカーマン関数の逆関数(ほぼ定数)
操作
🔍 グループの代表を取得(find)
dsu = DSU(5)
representative = dsu.find(3) # 3のグループの代表を取得
Big O: O(α(n))
🔗 グループを統合(union)
dsu = DSU(5)
dsu.union(0, 1) # 0と1を同じグループに
dsu.union(2, 3) # 2と3を同じグループに
dsu.union(1, 2) # さらに統合
Big O: O(α(n))
✅ 連結判定
dsu = DSU(5)
dsu.union(0, 1)
dsu.union(2, 3)
dsu.connected(0, 1) # True
dsu.connected(0, 2) # False
Big O: O(α(n))
🌀 Iterable(全ノード確認)
dsu = DSU(5)
for i in range(5):
print(i, dsu.find(i)) # 各要素のグループ代表を表示
🔁 再帰(経路圧縮)
# find内部が再帰呼び出しになっている
# これにより経路圧縮が実現される
💡 実用例:グラフの連結成分数
def count_components(n, edges):
"""グラフの連結成分数を数える"""
dsu = DSU(n)
for u, v in edges:
dsu.union(u, v)
# 異なる代表の数を数える
components = set()
for i in range(n):
components.add(dsu.find(i))
return len(components)
💡 実用例:最小全域木(Kruskal 法)
def kruskal(n, edges):
"""Kruskal法で最小全域木を構築"""
dsu = DSU(n)
edges.sort(key=lambda x: x[2]) # 重みでソート
mst = []
total_weight = 0
for u, v, weight in edges:
if dsu.find(u) != dsu.find(v):
dsu.union(u, v)
mst.append((u, v))
total_weight += weight
return mst, total_weight
💡 実用例:島の数(Union-Find 版)
def num_islands_union_find(grid):
"""島の数をUnion-Findで数える"""
if not grid:
return 0
rows, cols = len(grid), len(grid[0])
dsu = DSU(rows * cols)
for i in range(rows):
for j in range(cols):
if grid[i][j] == '1':
# 上下左右の'1'と統合
for di, dj in [(0, 1), (1, 0)]:
ni, nj = i + di, j + dj
if 0 <= ni < rows and 0 <= nj < cols and grid[ni][nj] == '1':
dsu.union(i * cols + j, ni * cols + nj)
# 異なるグループの数を数える
components = set()
for i in range(rows):
for j in range(cols):
if grid[i][j] == '1':
components.add(dsu.find(i * cols + j))
return len(components)
🧮 Big-O まとめ
| 構造 | 探索 | 挿入 | 削除 | 備考 |
|---|---|---|---|---|
| list | O(n) | O(1)/O(n) | O(1)/O(n) | 配列ベース |
| deque | O(n) | O(1) | O(1) | 両端高速 |
| dict/set | O(1) | O(1) | O(1) | ハッシュ構造 |
| heapq | O(1)最小取得 | O(log n) | O(log n) | 優先度キュー |
| linked list(単) | O(n) | O(1)先頭 | O(1)先頭 | 末尾操作は O(n) |
| linked list(双) | O(n)探索 | O(1) | O(1) | LRU 対応 |
| Union-Find | - | O(α(n)) | - | ほぼ定数 |
🎯 データ構造選択指針
問題タイプ別の選択
| 問題の特徴 | 推奨データ構造 | 理由 |
|---|---|---|
| 順序が重要 |
list / deque
|
インデックスアクセス、順序保持 |
| 高速検索が必要 |
dict / set
|
O(1) の検索・挿入 |
| 最小/最大を頻繁に取得 | heapq |
O(1) で最小値取得 |
| 両端操作が多い | deque |
両端が O(1) |
| 重複排除 | set |
自動で重複排除 |
| 頻度カウント |
dict / Counter
|
キーでカウント管理 |
| グループ管理・連結判定 | Union-Find |
ほぼ定数時間で統合 |
| LRU キャッシュ |
dict + 双方向リスト
|
O(1) で削除・移動 |
もちろんです!
ここは “似てるけど実はまったく別物” なので、一度整理しておくと今後のDSAの理解が一気にラクになりますよ。
前向きにコツコツ覚えていけば、必ず力になります!
📌 サブセット / サブストリング / サブシークエンス の違い
① Subset(サブセット:部分集合)
順番は関係なし
選ぶだけでOK(飛ばしてOK)
- 集合(set)から要素をいくつか選び取ること
- 元の並び順を考えない
- 連続している必要もない
- 0個選んでもOK(∅)
✔ 例
[A, B, C] のサブセット
→ [], [A], [B], [C], [A,B], [A,C], [B,C], [A,B,C]
✔ よく使う場面
- 組み合わせ(combination)
- バックトラッキング
- ビットマスク
- パワーセットの列挙
② Substring(サブストリング:連続部分文字列)
順番固定、かつ連続していないとダメ
- 文字列または配列の 連続した範囲 を抜き出したもの
- スライスすれば作れるイメージ
✔ 例
"ABCDE" のサブストリング
→ "A", "AB", "ABC", "BCD", "ABCDE" など
("ACE" は連続してないので NG)
✔ よく使う場面
- スライディングウィンドウ
- 最長(最短)部分文字列問題
- 二重ループで取り得る全区間探索
③ Subsequence(サブシークエンス:部分列)
順番は守るけど、飛ばしてOK(非連続OK)
- 順番は元と同じでなきゃいけない
- ただし、途中を抜かしてもよい
✔ 例
"ABCDE" のサブシークエンス
→ "A", "ACE", "ABD", "ABCDE"
(順番が崩れる "CA" は NG)
✔ よく使う場面
- 動的計画法(LCS, LIS など)
- 再帰・バックトラッキング
- 組み合わせ探索に近い考え方
🎯 3つの違いを一発で理解する図
| 種類 | 連続? | 順番? | 例 (ABCDE) |
|---|---|---|---|
| Subset | × | ×(順番気にしない) | {A, C, E} |
| Substring | 〇(必須) | 〇 | "BCD" |
| Subsequence | ×(不要) | 〇必須 | "ACE" |
💡 イメージで覚えると一瞬で区別できる
- Subset → 「袋から選ぶだけ」
- Substring → 「ハサミで連続部分だけ切り取る」
- Subsequence → 「飛び飛びでも並びは守る」
よくある問題パターンと解法
| 問題パターン | データ構造 | テクニック |
|---|---|---|
| 2 つの和 / 3 つの和 | dict |
補数を記録 |
| スライディングウィンドウ | deque |
両端操作で最適化 |
| K 個の最大/最小 | heapq |
サイズ k のヒープ |
| 重複検出 | set |
存在判定で O(1) |
| パリンドローム | deque |
両端から比較 |
| グラフ探索(BFS) | deque |
キューとして使用 |
| グラフ探索(DFS) |
list (スタック) |
再帰またはスタック |
| 連結成分 | Union-Find |
グループ統合 |
| 最小全域木 |
Union-Find + heapq
|
Kruskal 法 |
| LRU キャッシュ |
dict + 双方向リスト
|
O(1) 操作 |
💪 実践テクニック集
1. ダミーノードでエッジケースを簡略化
# Linked List で先頭削除のエッジケースを回避
dummy = Node(0)
dummy.next = head
# これで head が None でも統一的な処理が可能
2. スローファストポインタ(2 つのポインタ)
# サイクル検出、中間取得、n 番目取得など
slow = fast = head
while fast and fast.next:
slow = slow.next
fast = fast.next.next
3. 辞書で補数を記録(Two Sum パターン)
seen = {}
for i, num in enumerate(nums):
complement = target - num
if complement in seen:
return [seen[complement], i]
seen[num] = i
4. ヒープで K 個を維持
# K 個の最大要素を保持
min_heap = []
for num in nums:
heapq.heappush(min_heap, num)
if len(min_heap) > k:
heapq.heappop(min_heap) # 最小値を削除
5. デフォルト値でコードを簡潔に
from collections import defaultdict
count = defaultdict(int)
count[key] += 1 # エラーにならない
6. 集合演算で集合問題を解決
# 共通要素
common = set1 & set2
# 差集合
diff = set1 - set2
⚠️ よくある落とし穴
1. リストの先頭操作は O(n)
# ❌ 悪い例
li.insert(0, x) # O(n)
li.pop(0) # O(n)
# ✅ 良い例
dq.appendleft(x) # O(1)
dq.popleft() # O(1)
2. 辞書のキー存在確認
# ❌ 悪い例(KeyError の可能性)
value = d[key]
# ✅ 良い例
value = d.get(key, default_value)
3. ヒープは最小ヒープ
# 最大ヒープが必要な場合
heapq.heappush(heap, -value) # 負の値を使う
max_val = -heapq.heappop(heap)
4. 集合の順序(Python 3.7+ は保持)
# Python 3.6 以下では順序が保証されない
# 順序が必要なら list(dict.fromkeys(nums))
5. リストのスライシングは O(k)
# 大きなリストのスライシングは注意
large_slice = li[0:1000000] # O(1000000)
🗺️ 問題解決フローチャート
問題を読む
↓
何を求めているか?
↓
┌─────────────────┐
│ 順序が重要? │ → Yes → list / deque
└─────────────────┘
↓ No
┌─────────────────┐
│ 高速検索必要? │ → Yes → dict / set
└─────────────────┘
↓ No
┌─────────────────┐
│ 最小/最大取得? │ → Yes → heapq
└─────────────────┘
↓ No
┌─────────────────┐
│ グループ管理? │ → Yes → Union-Find
└─────────────────┘
↓ No
┌─────────────────┐
│ 両端操作多い? │ → Yes → deque
└─────────────────┘
↓ No
→ 基本は list で開始
🎓 実践的な問題解決アプローチ
ステップ 1: 問題を理解する
- 入力・出力の形式を確認
- 制約条件を確認(n の範囲、時間制限)
- エッジケースを考える
ステップ 2: データ構造を選択
- 必要な操作をリストアップ
- 操作の頻度を考慮
- 時間・空間計算量を確認
ステップ 3: アルゴリズムを設計
- ブルートフォースから始める
- 最適化の余地を探す
- データ構造の特性を活用
ステップ 4: 実装
- エッジケースを最初に処理
- 変数名を明確に
- コメントで意図を明確に
ステップ 5: テスト
- エッジケースをテスト
- 時間制限内に動作するか確認
🏁 まとめ
- for ループ:反復的処理で全体走査
- 再帰:構造を"分割して処理"する強力な手段
- 単方向/双方向リスト:削除コストを意識して使い分け
- データ構造選択:問題の特徴から最適な構造を選ぶ
- 実践テクニック:パターンを覚えて応用する
このチートシートを眺めるだけで、
どんなアルゴリズム問題にも「どの武器で戦うか」がすぐ浮かびます ⚔️
実践のコツ:
- 問題パターンを覚える
- データ構造の特性を理解する
- エッジケースを最初に考える
- 時間計算量を常に意識する
これでコーディング面接も競技プログラミングも怖くない! 🚀
Discussion