✈

Juliaの型推論アルゴリズムを実装する

2020/10/25に公開

Julia

先日書いた記事ではJuliaの型推論について、特にその機能の1つであるisaを使って条件分岐した先のブロックにおけるflow-sensitivityについて調べてみました。

この記事ではより基礎的な部分に注目して、Juliaの型推論のアルゴリズム(の一部)を理解し、実装してみようと思います。今回紹介する技術はより一般にプログラムの「抽象解釈」("abstract interpretation", "data-flow analysis")と呼ばれているもので、実際に実装するのも"constant folding"(「定数畳み込み」)と呼ばれる一般的なコンパイラ最適化問題です。なのでJuliaに興味がない人にも読んでいただけると嬉しいです。

アルゴリズム

data flow problem

"a data-flow problem"(抽象解釈問題)は以下の4つの要素を用いて定義します:

$P = I_0 ... I_n \in \text{Instr}$ : プログラム
$L = <A, \sqcup, \sqcap>$ : $P$ が取りうる抽象値のlattice^[1]
$![.!] : \text{Instr} \rightarrow (A \rightarrow A)$ : instruction $\text{Instr}$ がプログラムの抽象状態 $A$ に対してどのように作用するのかを与えるプログラムの抽象的な意味論("abstract semantics")
$a_0 \in A$ : プログラムの初期状態

ここで:

$\text{Instr}$ : プログラムを構成する基本的な"instructions"(命令たち)。条件分岐を起こすinstructionと、そうでないものが区別されていればなんでも良い
$A$ : プログラムの抽象状態を表現する集合^[2]
$\sqcup, \sqcap$ : それぞれjoinとmeet^[1:1]に対応する演算で、 $A$ に対して作用する

$P, L, ![.!]$ の具体的な中身はそれぞれの抽象解釈問題ごとに決まります。

"A Graph-Free Approach to Data-Flow Analysis"

data-flow problemを解くアルゴリズムは、Muchnick, Steven S., and Neil D. Jones. "Program flow analysis: Theory and applications." 1981.で提案された、basic blockをノードとするをグラフ("BB graph")をコアなデータ構造として用いるアルゴリズムが、de facto standardとなっていたようです。

Mohnen, Markus. “A Graph-Free Approach to Data-Flow Analysis.” CC (2002).はそのアルゴリズムをグラフを明示的なデータ構造として用いないように拡張したアルゴリズムを提案しました。

データ構造としてのグラフを用いないことで以下のような恩恵が得られることを実験的に示しています:

メモリ効率の改善: 多くの実験ケースでメモリ使用率を1/3程度に減らしつつ、実行時間のトレードオフは無視できるレベルであった
実装が容易: BB graphを構築する必要がない

論文で提案されているアルゴリズムを理解しやすくするために、まずは具体的な問題を考えてみましょう。

問題設定: constant folding propagation problem

この記事ではdata-flow problemの一例として、"constant folding"(「定数畳み込み」)を考えます。

constant folding propagationは、コンパイル時に分かる定数をできるだけ見つけて実行時の計算と置き換える、というコンパイラ最適化技術です。従ってそれを行うdata-flow problemとしては、プログラム中のそれぞれの時点における各変数が定数であるかどうか決めていく、という設定になります。

それでは早速 1.) プログラム $P$ , 2.) lattice $L$ , 3.) abstract semantics $![.!]$ , 4.) プログラムの初期状態 $a_0$ のそれぞれを確認しましょう。

問題設定 1. プログラム $P$

以下では簡単のため、プログラム $P$ は整数に対する演算のみを行うものとし、 $\text{Instr}$ としては以下の3つのみを考えることにします:

assignment: lhs := rhs
unconditional branching: goto instruction
conditional branching: condition && goto instruction

問題設定 2. lattice $L$

プログラム $P$ に含まれる各変数が取りうる抽象値 $C$ としては以下のものだけを考えます:

$\top$ : latticeの頂に位置する
$c \in \mathbb{N}$ : 定数
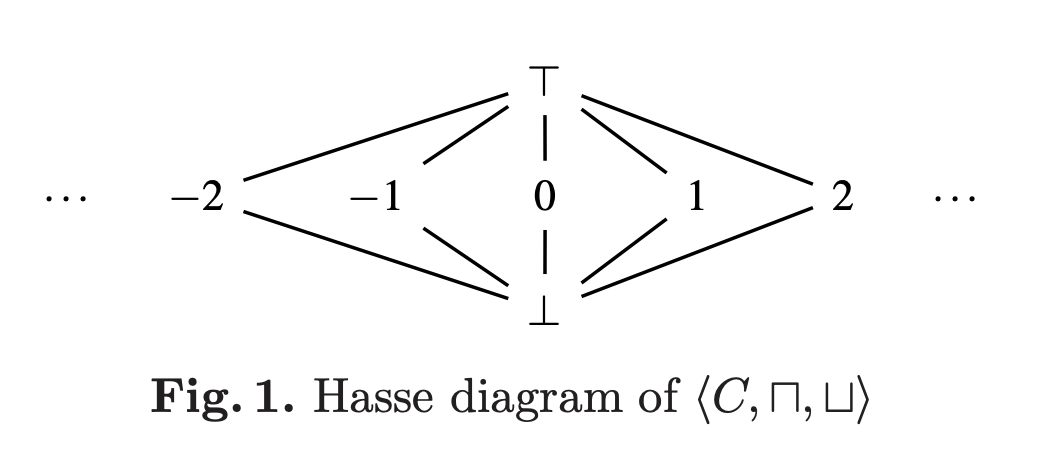
$\bot$ : latticeの底に位置する

$\top$ と $\bot$ の直観的な意味として、論文では以下のように説明されています:

$\top$ : "non constant due to missing information"
$\bot$ : "non constant due to conflict"

$C$ の順序関係を次のように定義します: $c_1 \le c_2$ iff a) $c_1 = c_2$ , b) $c_1 = \bot$ , c) $c_2 = \top$

$C$ は次の画像のようなフラットなlatticeとなります:
lattice

プログラム $P$ の各instructionにおける抽象状態 $A$ は、 $X$ をプログラム $P$ 中の変数の集合として、次のようなmapとして表現できます:

A := X \rightarrow C

$A$ に対する $\sqcup, \sqcap$ 演算は、 $A$ 中の変数のそれぞれの抽象値 $C$ に対しpair-wiseに行うような演算として自然に考えることができます。

問題設定 3. abstract semantics $![.!]$

プログラム $P$ のabstract semantics $![.!]$ を考えましょう。 $P$ を構成する各instructionはそれぞれの抽象状態に対して次のような作用を与えます:

assignment: lhs := rhs: rhsが定数である時のみその定数値をlhsに代入、それ以外の時は $\bot$ を代入
unconditional branching (goto instruction): 抽象状態を変化させない
conditional branching (condition && goto instruction): 抽象状態を変化させない

問題設定 4. プログラムの初期状態 $a_0$

論文ではconstant folding propagation problemのプログラムの初期状態 $a_0$ は $\bot$ で初期化するとしていますが、おそらく間違いです。直観的な意味からも、プログラムの初期状態では各変数は"non constant due to missing information"と解釈されるべきなので、 $\top$ で初期化されるべきでしょう:

a_0 := X \rightarrow \top

アルゴリズム

以上1.~4.でdata-flow problemのセットアップができました。

論文ではそのdata-flow problemを解くアルゴリズムとして以下のアルゴリズムが提案されています:
algorithm

このアルゴリズムの直観的な理解としては以下のようになります:

プログラム自身がinstruction levelでabstract semantics $![.!]$ を通してその抽象状態に作用する
アルゴリズムは現在のinstruction $I$ を示す現在のprogram counter $pc$ と、作用が計算されるべき残りのinstruction達(に対応する $pc$ )を保持するworking set $W$ を更新しながら動作する
現在のinstruction $I$ の抽象状態は、 $I$ が到達する可能性があるinstruction全てに伝播する
ただし、現在のinstruction $I$ の抽象状態は、伝播する先のinstructionの抽象状態を変化させる場合にのみ伝播する

3.はアルゴリズム中の $I_{pc} = (\text{if} \psi \text{goto} l)$ の箇所に相当します。これはつまり、このアルゴリズムは実際のプログラム実行とは異なり、条件分岐において両方の分岐先を勘定するということです。

4.はアルゴリズム中の $\text{if} new < s_{pc'}$ と $\text{if} new < s_{l}$ の箇所に相当します。論文では、「現在のinstructionの抽象状態が伝播先のinstructionの抽象状態を変化させるかどうか」の判定条件に抽象状態 $A$ のlattice $L$ における順序関係 $<$ を使い、 $<$ は以下の条件と等しいとしています:

new < s_{pc'} \equiv (new \sqcap s_{pc'} = new) \land (new \ne s_{pc'})

つまり、現在のinstruction $I$ の抽象状態 $new$ は、それが伝播先のinstructionの状態 $s_{pc'}$ (あるいはunconditional branching instructionの状態 $s_l$ )よりもlattice $L$ においてより低い位置にあるときにのみ、伝播します。したがって、各instructionの抽象状態 $A := X \rightarrow C$ は、常に $C$ がlattice $L$ の下側へのみ遷移するように更新されるため、lattice $L$ の高さが有限であればこのアルゴリズムは必ず収束します。

example program `prog0` and tracing

プログラム $P$ の具体例として、以下のプログラムprog0があるとしましょう:

prog0

0 ─ I₀ = x := 1
│   I₁ = y := 2
│   I₂ = z := 3
└── I₃ = goto I₈
1 ─ I₄ = r := y + z
└── I₅ = if x ≤ z goto I₇
2 ─ I₆ = r := z + y
3 ─ I₇ = x := x + 1
4 ─ I₈ = if x < 10 goto I₄

(最左列の番号はbasic blockに対応する番号です。この記事で紹介するアルゴリズムでは使用されません。)

論文では、prog0に対する上記アルゴリズムのtracingの例として以下の表を載せています:
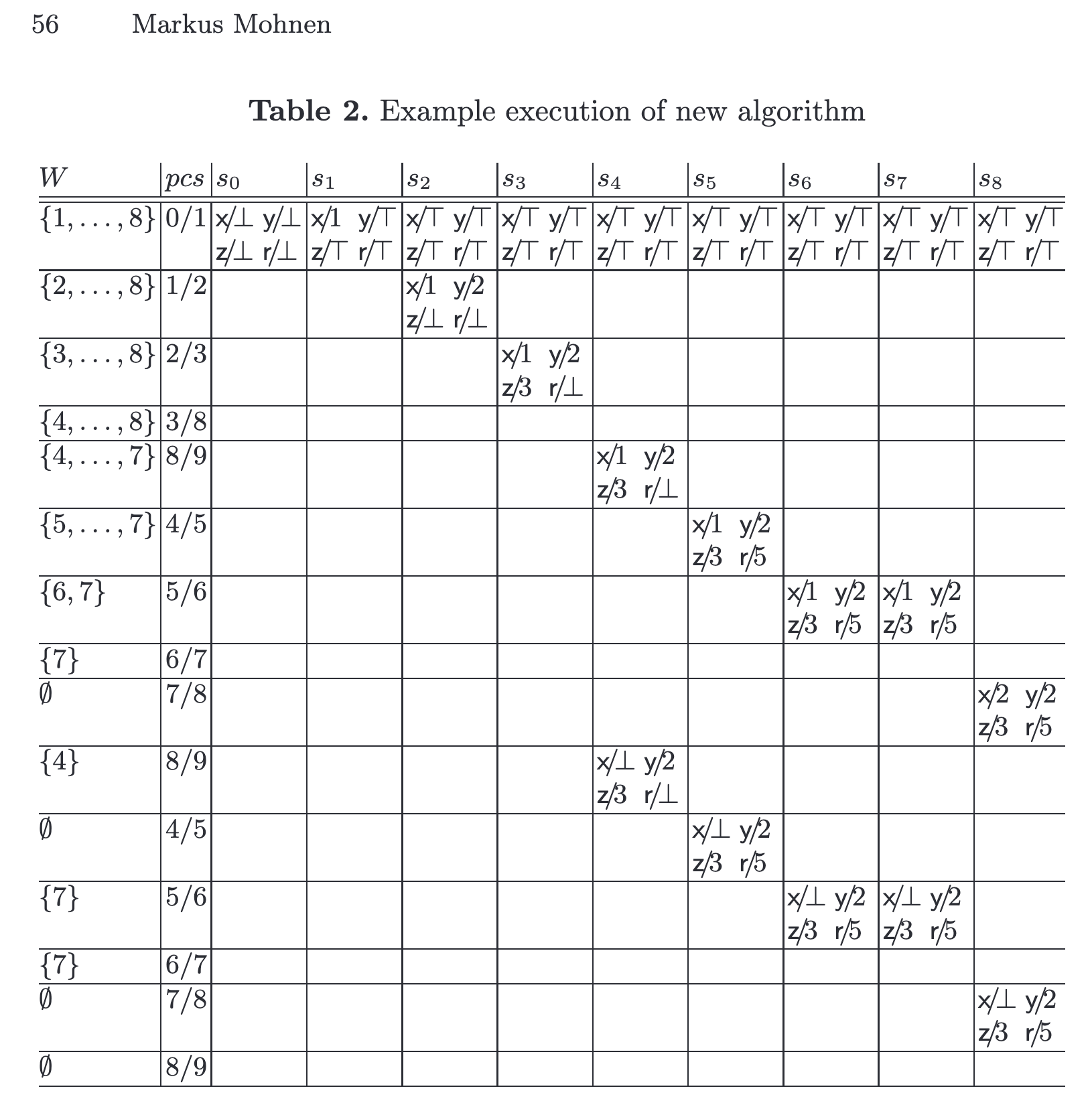
tracing example

最終的な状態 $s_8$ において、prog0中にない「rが定数5である」という情報が現れているのが分かると思います。

実装

前置きが長くなりましたが、それでは早速Juliaを用いて以上の問題設定とアルゴリズムを表現してみましょう。
前節と同じく、まず問題設定を記述し、次にアルゴリズムを実装します。

問題設定: constant folding propagation example

問題設定 1. プログラム $P$

abstract type Exp end

struct Sym <: Exp
    name::Symbol
end

struct Num <: Exp
    val::Int
end

struct Call <: Exp
    head::Sym
    args::Vector{Exp}
end

abstract type Instr end

struct Assign <: Instr
    lhs::Sym
    rhs::Exp
end

struct Goto <: Instr
    label::Int
end

struct GotoIf <: Instr
    label::Int
    cond::Exp
end

const Program = Vector{Instr}

Vector{Instr} (alias for Array{Instr, 1})

問題設定 2. lattice $L$

プログラムの抽象状態 $A := X \rightarrow C$ を表現します。

まず、プログラム中の各変数が取りうる抽象値 $C$ と、その順序関係を定義します:

# partial order, meet, join, top, bottom, and their identities

import Base: ≤, ==, <, show

abstract type LatticeElement end

struct Const <: LatticeElement
    val::Int
end

struct TopElement <: LatticeElement end
struct BotElement <: LatticeElement end

const ⊤ = TopElement()
const ⊥ = BotElement()

show(io::IO, ::TopElement) = print(io, '⊤')
show(io::IO, ::BotElement) = print(io, '⊥')

≤(x::LatticeElement, y::LatticeElement) = x≡y
≤(::BotElement,      ::TopElement)      = true
≤(::BotElement,      ::LatticeElement)  = true
≤(::LatticeElement,  ::TopElement)      = true

# NOTE: == and < are defined such that future LatticeElements only need to implement ≤
==(x::LatticeElement, y::LatticeElement) = x≤y && y≤x
<(x::LatticeElement,  y::LatticeElement) = x≤y && !(y≤x)

# join
⊔(x::LatticeElement, y::LatticeElement) = x≤y ? y : y≤x ? x : ⊤

# meet
⊓(x::LatticeElement, y::LatticeElement) = x≤y ? x : y≤x ? y : ⊥

⊓ (generic function with 1 method)

次に、抽象状態 $A$ を各変数 $X$ から抽象値 $C$ へのmapとして表現し、その順序関係 $<$ を定義します:

# NOTE: the paper (https://api.semanticscholar.org/CorpusID:28519618) uses U+1D56E MATHEMATICAL BOLD FRAKTUR CAPITAL C for this
const AbstractState = Dict{Symbol,LatticeElement}

# extend lattices of values to lattices of mappings of variables to values;
# ⊓ and ⊔ operate pair-wise, and from there we can just rely on the Base implementation for
# dictionary equiality comparison

⊔(X::AbstractState, Y::AbstractState) = AbstractState( v => X[v] ⊔ Y[v] for v in keys(X) )
⊓(X::AbstractState, Y::AbstractState) = AbstractState( v => X[v] ⊓ Y[v] for v in keys(X) )

<(X::AbstractState, Y::AbstractState) = X⊓Y==X && X≠Y

< (generic function with 85 methods)

問題設定 3. abstract semantics $![.!]$

abstract semantics $![.!]$ は、実際のJuliaのexecutionを用いて簡単に実装できます。
Callのhead::Symbol fieldから実際の演算メソッドをgetfieldを用いて復元します。

abstract_eval(x::Num, s::AbstractState) = Const(x.val)

abstract_eval(x::Sym, s::AbstractState) = get(s, x.name, ⊥)

function abstract_eval(x::Call, s::AbstractState)
    f = getfield(@__MODULE__, x.head.name)

    argvals = Int[]
    for arg in x.args
        arg = abstract_eval(arg, s)
        arg === ⊥ && return ⊥ # bail out if any of call arguments is non-constant
        push!(argvals, unwrap_val(arg))
    end

    return Const(f(argvals...))
end

# unwrap our lattice representation into actual Julia value
unwrap_val(x::Num)   = x.val
unwrap_val(x::Const) = x.val

unwrap_val (generic function with 2 methods)

問題設定 4. プログラムの初期状態 $a_0$

論文の例を修正し、 $\top$ で初期化します:

a₀ = AbstractState(:x => ⊤, :y => ⊤, :z => ⊤, :r => ⊤)

Dict{Symbol, LatticeElement} with 4 entries:
  :y => ⊤
  :z => ⊤
  :r => ⊤
  :x => ⊤

example program `prog0`

アルゴリズムを実装する前に、プログラム例prog0を表現しましょう。

ナイーブに表現するとこのようになると思います:

prog0 = [Assign(Sym(:x), Num(1)),                              # I₀
         Assign(Sym(:y), Num(2)),                              # I₁
         Assign(Sym(:z), Num(3)),                              # I₂
         Goto(8),                                              # I₃
         Assign(Sym(:r), Call(Sym(:(+)), [Sym(:y), Sym(:z)])), # I₄
         GotoIf(7, Call(Sym(:(≤)), [Sym(:x), Sym(:z)])),       # I₅
         Assign(Sym(:r), Call(Sym(:(+)), [Sym(:z), Sym(:y)])), # I₆
         Assign(Sym(:x), Call(Sym(:(+)), [Sym(:x), Num(1)])),  # I₇
         GotoIf(4, Call(Sym(:(<)), [Sym(:x), Num(10)])),       # I₈
         ]::Program

9-element Vector{Instr}:
 Assign(Sym(:x), Num(1))
 Assign(Sym(:y), Num(2))
 Assign(Sym(:z), Num(3))
 Goto(8)
 Assign(Sym(:r), Call(Sym(:+), Exp[Sym(:y), Sym(:z)]))
 GotoIf(7, Call(Sym(:≤), Exp[Sym(:x), Sym(:z)]))
 Assign(Sym(:r), Call(Sym(:+), Exp[Sym(:z), Sym(:y)]))
 Assign(Sym(:x), Call(Sym(:+), Exp[Sym(:x), Num(1)]))
 GotoIf(4, Call(Sym(:<), Exp[Sym(:x), Num(10)]))

ちょっと見辛いですね。
そこで、Juliaの強力なメタプログラミング機能を用いて、Juliaのsyntaxから今回ターゲットとするinstruction levelのプログラム $P$ を生成するマクロ@progを記述しましょう^[3]。
surface syntax ASTに対するpattern-matchingを行えるパッケージMacroTools.jlを使います:

using MacroTools

macro prog(blk)
    Instr[Instr(x) for x in filter(!islnn, blk.args)]::Program
end

function Instr(x)
    if @capture(x, lhs_ = rhs_)               # => Assign
        Assign(Instr(lhs), Instr(rhs))
    elseif @capture(x, @goto label_)          # => Goto
        Goto(label)
    elseif @capture(x, cond_ && @goto label_) # => GotoIf
        GotoIf(label, Instr(cond))
    elseif @capture(x, f_(args__))            # => Call
        Call(Instr(f), Instr.(args))
    elseif isa(x, Symbol)                     # => Sym
        Sym(x)
    elseif isa(x, Int)                        # => Num
        Num(x)
    else
        error("invalid expression: $(x)")
    end
end

islnn(@nospecialize(_)) = false
islnn(::LineNumberNode) = true

islnn (generic function with 2 methods)

prog0を生成してみます:

prog0 = @prog begin
    x = 1             # I₀
    y = 2             # I₁
    z = 3             # I₂
    @goto 8           # I₃
    r = y + z         # I₄
    x ≤ z && @goto 7  # I₅
    r = z + y         # I₆
    x = x + 1         # I₇
    x < 10 && @goto 4 # I₈
end

9-element Vector{Instr}:
 Assign(Sym(:x), Num(1))
 Assign(Sym(:y), Num(2))
 Assign(Sym(:z), Num(3))
 Goto(8)
 Assign(Sym(:r), Call(Sym(:+), Exp[Sym(:y), Sym(:z)]))
 GotoIf(7, Call(Sym(:≤), Exp[Sym(:x), Sym(:z)]))
 Assign(Sym(:r), Call(Sym(:+), Exp[Sym(:z), Sym(:y)]))
 Assign(Sym(:x), Call(Sym(:+), Exp[Sym(:x), Num(1)]))
 GotoIf(4, Call(Sym(:<), Exp[Sym(:x), Num(10)]))

うまく $P$ が作れてますね :-)

アルゴリズム

それでは本題のアルゴリズムを実装してみましょう。論文で紹介されているままに実装すると次のようになります:

function max_fixed_point(prog::Program, a₀::AbstractState, eval)
    n = length(prog)
    init = AbstractState( v => ⊤ for v in keys(a₀) )
    s = [ a₀; [ init for i = 2:n ] ]
    W = BitSet(0:n-1)

    while !isempty(W)
        pc = first(W)
        while pc ≠ n
            delete!(W, pc)
            I = prog[pc+1]
            new = s[pc+1]
            if isa(I, Assign)
                # for an assignment, outgoing value is different from incoming
                new = copy(new)
                new[I.lhs.name] = eval(I.rhs, new)
            end

            if isa(I, Goto)
                pc´ = I.label
            else
                pc´ = pc+1
                if isa(I, GotoIf)
                    l = I.label
                    if new < s[l+1]
                        push!(W, l)
                        s[l+1] = new
                    end
                end
            end
            if pc´≤n-1 && new < s[pc´+1]
                s[pc´+1] = new
                pc = pc´
            else
                pc = n
            end
        end
    end

    return s
end

max_fixed_point (generic function with 1 method)

論文では0-indexでプログラムなどを記述しているので、この記事でもそのまま表現していますが、Juliaの配列のindexingは1から始まるので、s[pc´+1]などとしてindexingを調整していることに注意してください。

それでは実行してみましょう！

max_fixed_point(prog0, a₀, abstract_eval)

9-element Vector{Dict{Symbol, LatticeElement}}:
 Dict(:y => ⊤, :z => ⊤, :r => ⊤, :x => ⊤)
 Dict(:y => ⊤, :z => ⊤, :r => ⊤, :x => Const(1))
 Dict(:y => Const(2), :z => ⊤, :r => ⊤, :x => Const(1))
 Dict(:y => Const(2), :z => Const(3), :r => ⊤, :x => Const(1))
 Dict(:y => Const(2), :z => Const(3), :r => ⊤, :x => Const(1))
 Dict(:y => Const(2), :z => Const(3), :r => Const(5), :x => Const(1))
 Dict(:y => Const(2), :z => Const(3), :r => Const(5), :x => Const(1))
 Dict(:y => Const(2), :z => Const(3), :r => Const(5), :x => Const(1))
 Dict(:y => Const(2), :z => Const(3), :r => ⊤, :x => Const(1))

... 論文に載っているtrace例と違う出力が出ています。

先に結論をいうと、実はこれは論文のアルゴリズムが一部間違っているからなのですが、詳しくみてみましょう^[4]。

まず、先ほど紹介したtrace例は実は不完全であり、実際にアルゴリズムを動かすと、表で空欄になっている左から11行目上から5行目でI₃ = goto I₈の状態 $s_3$ がI₈ = if x < 10 goto I₄の状態 $s_8$ にも伝播しているはずで、 $s_8 := \text{x}/1 \text{y}/2 \text{z}/3 \text{r}/\top$ となっています。
そうすると、左から11行目上から10行目でI₇ = x := x + 1の状態 $s_7$ を $s_8$ へ伝播させるための条件 $s_8 < s_7$ が成り立たず、そのまま $W$ が空となりアルゴリズムは停止します(i.e. この記事の実装でいうとnew < s[pc´+1]がfalseとなります)。

上の実装は論文に忠実に従っているので、以上で説明した挙動の通りにアルゴリズムが停止してしまいます。さぁ困った。

論文のアルゴリズムをデバッグ

論文のアルゴリズムの問題点は、端的に言えば、「伝播する先の抽象状態を変化させるかどうか」という判定に抽象状態同士の順序関係を用いるとうまく状態が伝播しない、ということです。
つまりこの場合、 $s_8$ の前状態s[pc´+1]( $\text{x}/1 \text{y}/2 \text{z}/3 \text{r}/\top$ )と現状態new = s[pc´]( $\text{x}/2 \text{y}/2 \text{z}/3 \text{r}/5$ )の間にはnew < s[pc´+1]という順序関係は成立しませんが^[5]、newの状態をs[pc´+1]へ伝播させ、s[pc´+1]を新たな状態( $\text{x}/\bot \text{y}/2 \text{z}/3 \text{r}/5$ )へと更新したいわけです。

従ってアルゴリズムの修正の方向性としては、以下のようになります:

現状態 $new$ と前状態 $s_{pc'}$ の順序関係 $new < s_{pc'} \equiv (new \sqcap s_{pc'} = new) \land (new \ne s_{pc'})$ を用いず、 $new$ の変化を $s_{pc'}$ へ伝えたい
一方で、アルゴリズムの停止性を保つために、 $new$ の変更は、新しい状態が前状態よりもlattice $L$ において低い位置にいくように、伝播される必要がある

これらをコードに落とし込むと次のようになります:

「伝播する先の抽象状態を変化させるかどうか」の判定に、状態同士のequivalenceを用いる
状態の更新に、⊓(meet: 最大下界を計算)を用いて、常に更新後の状態が更新前の状態よりも $L$ において低い位置にいくようにする

というわけでmax_fixed_pointに以下のdiffをあてましょう:

diff --git a/articles/dataflow.jl b/articles/dataflow.jl
index c43e086..c41ffa7 100644
--- a/articles/dataflow.jl
+++ b/articles/dataflow.jl
@@ -156,14 +156,14 @@ function max_fixed_point(prog::Program, a₀::AbstractState, eval)
                 pc´ = pc+1
                 if isa(I, GotoIf)
                     l = I.label
-                    if new < s[l+1]
+                    if new ≠ s[l+1]
                         push!(W, l)
-                        s[l+1] = new
+                        s[l+1] = new ⊓ s[l+1]
                     end
                 end
             end
-            if pc´≤n-1 && new < s[pc´+1]
-                s[pc´+1] = new
+            if pc´≤n-1 && new ≠ s[pc´+1]
+                s[pc´+1] = new ⊓ s[pc´+1]
                 pc = pc´
             else
                 pc = n

修正版アルゴリズム

それでは修正版のアルゴリズムで試してみましょう:

# NOTE: in this problem, we make sure that states will always move to _lower_ position in lattice, so
# - initialize states with `⊤`
# - we use `⊓` (meet) operator to update states,
# - and the condition we use to check whether or not the statement makes a change is `new ≠ prev`
function max_fixed_point(prog::Program, a₀::AbstractState, eval)
    n = length(prog)
    init = AbstractState( v => ⊤ for v in keys(a₀) )
    s = [ a₀; [ init for i = 2:n ] ]
    W = BitSet(0:n-1)

    while !isempty(W)
        pc = first(W)
        while pc ≠ n
            delete!(W, pc)
            I = prog[pc+1]
            new = s[pc+1]
            if isa(I, Assign)
                # for an assignment, outgoing value is different from incoming
                new = copy(new)
                new[I.lhs.name] = eval(I.rhs, new)
            end

            if isa(I, Goto)
                pc´ = I.label
            else
                pc´ = pc+1
                if isa(I, GotoIf)
                    l = I.label
                    if new ≠ s[l+1]
                        push!(W, l)
                        s[l+1] = new ⊓ s[l+1]
                    end
                end
            end
            if pc´≤n-1 && new ≠ s[pc´+1]
                s[pc´+1] = new ⊓ s[pc´+1]
                pc = pc´
            else
                pc = n
            end
        end
    end

    return s
end

max_fixed_point(prog0, a₀, abstract_eval) # The solution contains the `:r => Const(5)`, which is not found in the program

9-element Vector{Dict{Symbol, LatticeElement}}:
 Dict(:y => ⊤, :z => ⊤, :r => ⊤, :x => ⊤)
 Dict(:y => ⊤, :z => ⊤, :r => ⊤, :x => Const(1))
 Dict(:y => Const(2), :z => ⊤, :r => ⊤, :x => Const(1))
 Dict(:y => Const(2), :z => Const(3), :r => ⊤, :x => Const(1))
 Dict(:y => Const(2), :z => Const(3), :r => Const(5), :x => ⊥)
 Dict(:y => Const(2), :z => Const(3), :r => Const(5), :x => ⊥)
 Dict(:y => Const(2), :z => Const(3), :r => Const(5), :x => ⊥)
 Dict(:y => Const(2), :z => Const(3), :r => Const(5), :x => ⊥)
 Dict(:y => Const(2), :z => Const(3), :r => Const(5), :x => ⊥)

Hooray ! 見事、 $I_8$ の状態 $s_8$ に該当するDict(:y => Const(2), :z => Const(3), :r => Const(5), :x => ⊥)で、「rが定数Const(5)である」という情報が見つけられていますね。

Julia自身の型推論と比較してみる

ところで、Juliaの型推論は大きく以下の2つのパートから成り立っています:

part 1. 推論フレームのスコープ内でローカルに行う推論
part 2. 関数呼び出しを跨いで行う推論

part 1.がJuliaの型推論プロセスのコアとなるルーチンで、この記事で紹介している“A Graph-Free Approach to Data-Flow Analysis.”で提唱されたアルゴリズムをベースとしています。part 2.でそのアルゴリズムを相互再帰呼び出しも扱えるように拡張しており、そちらの詳細についてはJuliaのcreatorの1人であるJeff BezansonさんのPh.D thesisが詳しいですが、この記事では触れません。

となると、Juliaの型推論ルーチンがこの記事と同様に元論文のアルゴリズムを修正しているのかどうか、prog0に対して正しく動くのかどうか気になるところです。

まず試してみる

まずはprog0に対応するJuliaコードを作って、型推論を走らせてみましょう。Juliaの型推論はdata-flow analysisによりJuliaコードの型付けを行うことを目的としていますが、推論の精度を高めるために定数伝播も行います。もしJuliaの型推論ルーチンが正しく動くならば推論の結果に「rが定数5である」という情報が現れているはずです。

prog0をJuliaコードとしてそのまま表現すると以下のようになると思います:

begin
    begin
        @label I₀
        x = 1
    end
    ...
    begin
        @label I₅
        x ≤ z && @goto I₇
    end
    ...
end

やはり少し醜いので、この記事の $P = I_0 ... I_n \in \text{Instr}$ の記述方法から実際に実行可能なJuliaコードを生成するマクロ@prog′を定義しましょう:

# generate valid Julia code from the "`Instr` syntax"
macro prog′(blk)
    prog′ = Expr(:block)
    bns = [gensym(Symbol(:instruction, i-1)) for i in 1:length(blk.args)] # pre-generate labels for all instructions

    for (i,x) in enumerate(filter(!islnn, blk.args))
        x = MacroTools.postwalk(x) do x
            return if @capture(x, @goto label_)
                Expr(:symbolicgoto, bns[label+1]) # fix `@goto i` into valid goto syntax
            else
                x
            end
        end

        push!(prog′.args, Expr(:block, Expr(:symboliclabel, bns[i]), x)) # label this statement
    end

    return prog′
end

@macroexpand @prog′ begin
    x = 1             # I₀
    y = 2             # I₁
    z = 3             # I₂
    @goto 8           # I₃
    r = y + z         # I₄
    x ≤ z && @goto 7  # I₅
    r = z + y         # I₆
    x = x + 1         # I₇
    x < 10 && @goto 4 # I₈
end

quote
    begin
        $(Expr(:symboliclabel, Symbol("#198###instruction0#249")))
        var"#210#x" = 1
    end
    begin
        $(Expr(:symboliclabel, Symbol("#199###instruction1#250")))
        var"#207#y" = 2
    end
    begin
        $(Expr(:symboliclabel, Symbol("#200###instruction2#251")))
        var"#208#z" = 3
    end
    begin
        $(Expr(:symboliclabel, Symbol("#201###instruction3#252")))
        $(Expr(:symbolicgoto, Symbol("#202###instruction8#257")))
    end
    begin
        $(Expr(:symboliclabel, Symbol("#203###instruction4#253")))
        var"#209#r" = var"#207#y" + var"#208#z"
    end
    begin
        $(Expr(:symboliclabel, Symbol("#204###instruction5#254")))
        var"#210#x" ≤ var"#208#z" && $(Expr(:symbolicgoto, Symbol("#205###instruction7#256")))
    end
    begin
        $(Expr(:symboliclabel, Symbol("#206###instruction6#255")))
        var"#209#r" = var"#208#z" + var"#207#y"
    end
    begin
        $(Expr(:symboliclabel, Symbol("#205###instruction7#256")))
        var"#210#x" = var"#210#x" + 1
    end
    begin
        $(Expr(:symboliclabel, Symbol("#202###instruction8#257")))
        var"#210#x" < 10 && $(Expr(:symbolicgoto, Symbol("#203###instruction4#253")))
    end
end

うまく生成できていますね。

それでは早速code_typedを用いて型推論の結果を確認してみましょう:

code_typed(; optimize = false) do
    @prog′ begin
        x = 1             # I₀
        y = 2             # I₁
        z = 3             # I₂
        @goto 8           # I₃
        r = y + z         # I₄
        x ≤ z && @goto 7  # I₅
        r = z + y         # I₆
        x = x + 1         # I₇
        x < 10 && @goto 4 # I₈

        x, y, z, r # to check the result of abstract interpretation
    end
end |> first

CodeInfo(
1 ─       Core.NewvarNode(:(r))::Any
│         (x = 1)::Core.Const(1)
│         (y = 2)::Core.Const(2)
│         (z = 3)::Core.Const(3)
└──       goto #6
2 ─       (r = y::Core.Const(2) + z::Core.Const(3))::Core.Const(5)
│   %7  = (x ≤ z::Core.Const(3))::Bool
└──       goto #4 if not %7
3 ─       goto #5
4 ─       (r = z::Core.Const(3) + y::Core.Const(2))::Core.Const(5)
5 ┄       (x = x + 1)::Int64
6 ┄ %12 = (x < 10)::Bool
└──       goto #8 if not %12
7 ─       goto #2
8 ─ %15 = Core.tuple(x, y::Core.Const(2), z::Core.Const(3), r::Core.Const(5))::Core.PartialStruct(NTuple{4, Int64}, Any[Int64, Core.Const(2), Core.Const(3), Core.Const(5)])
└──       return %15
) => NTuple{4, Int64}

8 ─ %15 = Core.tuple(x, y::Core.Const(2), z::Core.Const(3), r::Core.Const(5))::Core.PartialStruct(NTuple{4, Int64}, Any[Int64, Core.Const(2), Core.Const(3), Core.Const(5)])という出力に現れているように、Juliaの型推論ルーチンは正しく「rが定数(Julia compilerの表現としてはCore.Const(5))である」という情報を見つけることができていますね。

実行してみる

実行してみると、やはり期待通りr == 5という結果が得られているのが確認できます:

@prog′ begin
    x = 1             # I₀
    y = 2             # I₁
    z = 3             # I₂
    @goto 8           # I₃
    r = y + z         # I₄
    x ≤ z && @goto 7  # I₅
    r = z + y         # I₆
    x = x + 1         # I₇
    x < 10 && @goto 4 # I₈

    x, y, z, r # to check the result of actual execution
end

(10, 2, 3, 5)

Juliaの型推論の実装での修正を確認する

どうやらJuliaの型推論ルーチンも論文のアルゴリズムを修正しているようです。実際のコードを見て確認してみましょう。

先ほどの修正点に対応する箇所を紹介します:

これらをコードに落とし込むと次のようになります:

「伝播する先の抽象状態を変化させるかどうか」の判定に、状態同士のequivalenceを用いる

状態の更新に、⊓(meet: 最大下界を計算)を用いて、更新後の状態が更新前の状態よりも常に $L$ の低い位置にいくようにする

修正1. 「伝播する先の抽象状態を変化させるかどうか」の判定

Juliaの型推論実装において、抽象状態の更新に該当する箇所は次のコードになります:

https://github.com/JuliaLang/julia/blob/d474c98667db0bf4832e4eeb7beb0e8cfc8b7481/base/compiler/abstractinterpretation.jl#L1316: newstate_else = stupdate!(s[l], changes_else)
https://github.com/JuliaLang/julia/blob/d474c98667db0bf4832e4eeb7beb0e8cfc8b7481/base/compiler/abstractinterpretation.jl#L1415: newstate = stupdate!(s[pc´], changes)

supdate!は以下のような実装になっています：

https://github.com/JuliaLang/julia/blob/d474c98667db0bf4832e4eeb7beb0e8cfc8b7481/base/compiler/typelattice.jl#L268-L307

function stupdate!(state::VarTable, changes::StateUpdate)
    if !isa(changes.var, Slot)
        return stupdate!(state, changes.state)
    end
    newstate = false
    changeid = slot_id(changes.var::Slot)
    for i = 1:length(state)
        if i == changeid
            newtype = changes.vtype
        else
            newtype = changes.state[i]
        end
        oldtype = state[i]
        # remove any Conditional for this Slot from the vtable
        if isa(newtype, VarState)
            newtypetyp = newtype.typ
            if isa(newtypetyp, Conditional) && slot_id(newtypetyp.var) == changeid
                newtype = VarState(widenconditional(newtypetyp), newtype.undef)
            end
        end
        if schanged(newtype, oldtype)
            newstate = state
            state[i] = smerge(oldtype, newtype)
        end
    end
    return newstate
end

function stupdate!(state::VarTable, changes::VarTable)
    newstate = false
    for i = 1:length(state)
        newtype = changes[i]
        oldtype = state[i]
        if schanged(newtype, oldtype)
            newstate = state
            state[i] = smerge(oldtype, newtype)
        end
    end
    return newstate
end

どうやらschangedが状態の更新をするかどうかの判定を行っているようです。schangedはこのように実装されています:

https://github.com/JuliaLang/julia/blob/d474c98667db0bf4832e4eeb7beb0e8cfc8b7481/base/compiler/typelattice.jl#L236

@inline schanged(@nospecialize(n), @nospecialize(o)) = (n !== o) && (o === NOT_FOUND || (n !== NOT_FOUND && !issubstate(n, o)))

この記事と違って抽象状態 $A$ を比較するのではなく、各変数の抽象値 $C$ (この記事のLatticeElementに相当)を比較していますが、やはり $L$ の要素の順序関係ではなくequivalence((n !== o))を用いて判定を行っているのが分かると思います。

厳密に言うと...

やはり $L$ の要素の順序関係ではなくequivalence((n !== o))を用いて判定を行っている

という記述は厳密には正しくありません。

schangedの中に!issubstate(n, o)という条件があるのに気が付いた方もいるかもしれません。

https://github.com/JuliaLang/julia/blob/d474c98667db0bf4832e4eeb7beb0e8cfc8b7481/base/compiler/typelattice.jl#L224

issubstate(a::VarState, b::VarState) = (a.typ ⊑ b.typ && a.undef <= b.undef)

⊑はJuliaのtype latticeにおける半順序関係を計算します。つまり、!issubstate(n, o)は「更新後の状態が更新前の状態よりもlatticeにおいて低くない位置にある場合にのみ状態を更新する」ようにしているということです。

これをこの記事の実装に当てはめてみると、new < s[pc´+1]の代わりに!(new ≥ s[pc´+1])という条件を用いることを意味します。ややこしいですが、Juliaの型推論は抽象状態が更新される方向がこの記事のconstant folding propagationと逆向きなので、不等号の向きが逆になっていることに注意してください。

修正2. 状態の更新の修正

抽象値の更新はsmergeが行っているようです:

https://github.com/JuliaLang/julia/blob/d474c98667db0bf4832e4eeb7beb0e8cfc8b7481/base/compiler/typelattice.jl#L226-L233

function smerge(sa::Union{NotFound,VarState}, sb::Union{NotFound,VarState})
    sa === sb && return sa
    sa === NOT_FOUND && return sb
    sb === NOT_FOUND && return sa
    issubstate(sa, sb) && return sb
    issubstate(sb, sa) && return sa
    return VarState(tmerge(sa.typ, sb.typ), sa.undef | sb.undef)
end

やや複雑ですが、基本的にはtmergeが更新を引き受けているようです。tmergeはより複雑なのでここで紹介はしませんが、 $\sqcup$ (meet)に相当する演算を行うgeneric functionです。

なぜ $\sqcap$ ではなく $\sqcup$ なのでしょうか。Juliaの型推論ルーチンは最も抽象的な抽象値であるAnyを頂上とし下に行けば行くほど具体的な抽象値^[6] になるようなlatticeに対して動作し、状態がlatticeの底から上に登るように更新されていくので^[7] 、この記事で実装したconstant folding propagation problemとは逆方向に状態を遷移させていきます。そのため $\sqcap$ ではなく、 $\sqcap$ と対をなす演算 $\sqcup$ を用いているというわけです。

いずれにせよ、Juliaの型推論ルーチンも、論文のアルゴリズムをベースとしつつも、この記事と同様の修正をあてているのが分かると思います。

まとめと雑感

この記事では、Mohnen, Markus. “A Graph-Free Approach to Data-Flow Analysis.” CC (2002).で提案された、BB graphを明示的なデータ構造として用いずにプログラムの抽象解釈を行うことができるアルゴリズムを紹介し、実際に実装してみました。
実装する中で論文側の間違いを発見したわけですが、erattaも出ておらず、また論文を疑って間違いを修正するということは個人的には全く経験したことがなかったので、この記事の結論に辿り着くまでにだいぶ苦労しました。Akira Kawataさんが一緒に悩んでくれたので解決しました。この場で改めて感謝したいと思います。
また思いついた修正点と同様のコードがJuliaの型推論のルーチンにもあったのは、なんだか嬉しかったです。もしかしたらこの修正点の必要性は、この記事を読んだ方と、Juliaのcompilerの開発者の方しか気がついていないのかも知れません。今度Juliaのslackで聞いてみようと思います。

ノート

この記事の本体及び使用したコードはhttps://github.com/aviatesk/aviatesk-zenn-contentで公開しています。タイポや誤りなど見つけた際は是非この記事へコメントあるいはrepositoryの方へissue/PRをいただけると嬉しいです。
この記事は僕がメンテナをしているJuliaのliterate programming package Weave.jlを用いて、.jmdファイルからzennでpublishする用のmarkdownを生成しています。今後zennでJuliaに関する記事を掲載しようとしている方の参考になるかも知れません.

脚注

lattice: https://en.wikipedia.org/wiki/Lattice_(order) / join and meet: https://en.wikipedia.org/wiki/Join_and_meet ↩︎ ↩︎
論文では記号としてUnicode Character “𝕮” (U+1D56E)が用いられていますが、このフォントがKaTeXでサポートされていないのでこの記事では $A$ を用います。 ↩︎
他には、Base.convertをoverloadしてSymbolからSymなどへ自動的にpromoteされるようにすることで、SymやNumなどのconstructorの記述をせずにより簡潔に記述できるようにする、という手もあります。書くプログラムの見た目的にはナイーブな表現と近いものになります。 ↩︎
ちなみにerrataなどは出ていません。 ↩︎
ないしはs[pc´+1] < newという順序関係も成立しません。 ↩︎
つまりJuliaの型推論のlatticeの順序関係としては、例えば、⊥(Bottom) ⊑ Const(1) ⊑ Int ⊑ Union{String,Int} ⊑ ⊤(Any)というようになります。 ↩︎
Juliaの型推論は推論がうまくいかない場合、latticeの底に位置するCore.Bottomではなく、頂点に位置するAnyと推論することからも分かると思います。 ↩︎

アルゴリズム

data flow problem

"A Graph-Free Approach to Data-Flow Analysis"

問題設定: constant folding propagation problem

問題設定 1. プログラム P

問題設定 2. lattice L

問題設定 3. abstract semantics ![.!]

問題設定 4. プログラムの初期状態 a_0

アルゴリズム

example program prog0 and tracing

実装

問題設定: constant folding propagation example

問題設定 1. プログラム P

問題設定 2. lattice L

問題設定 3. abstract semantics ![.!]

問題設定 4. プログラムの初期状態 a_0

example program prog0

アルゴリズム

論文のアルゴリズムをデバッグ

修正版アルゴリズム

Julia自身の型推論と比較してみる

まず試してみる

Juliaの型推論の実装での修正を確認する

修正1. 「伝播する先の抽象状態を変化させるかどうか」の判定

修正2. 状態の更新の修正

まとめと雑感

ノート

Discussion

問題設定 1. プログラム $P$

問題設定 2. lattice $L$

問題設定 3. abstract semantics $![.!]$

問題設定 4. プログラムの初期状態 $a_0$

example program `prog0` and tracing

問題設定 1. プログラム $P$

問題設定 2. lattice $L$

問題設定 3. abstract semantics $![.!]$

問題設定 4. プログラムの初期状態 $a_0$

example program `prog0`