🌟

【Coursera】Introduction to Self-Driving Cars: Week6

2022/09/24に公開

coursera

Autonomous driving

tech

Courseraのトロント大学が提供している専門講座Self-Driving CarsのIntroduction to Self-Driving Carsコースのメモ

Week5はこちら

Lesson 1: Introduction to Lateral Vehicle Control

横方向制御の主な目的はPlanningモジュールで作成されるモーションプランを実行して経路に車両を正確に追従させること。蓄積された誤差を修正し、経路の変化に追従するためにステアリング角度を選択する。

横方向制御に必要なこと

車両位置と適切な経路座標との間の誤差を定義する。
ステアリング角度の制限を満たしながら誤差をゼロにする制御戦略を選択する。
Dynamicの制約や最大加速度、最小の揺れなどの望ましい乗り心地を考慮に入れる。
制御コマンドは利用可能なタイヤの力を認識し、誤差を修正する際に車両の能力を超えないようにする。

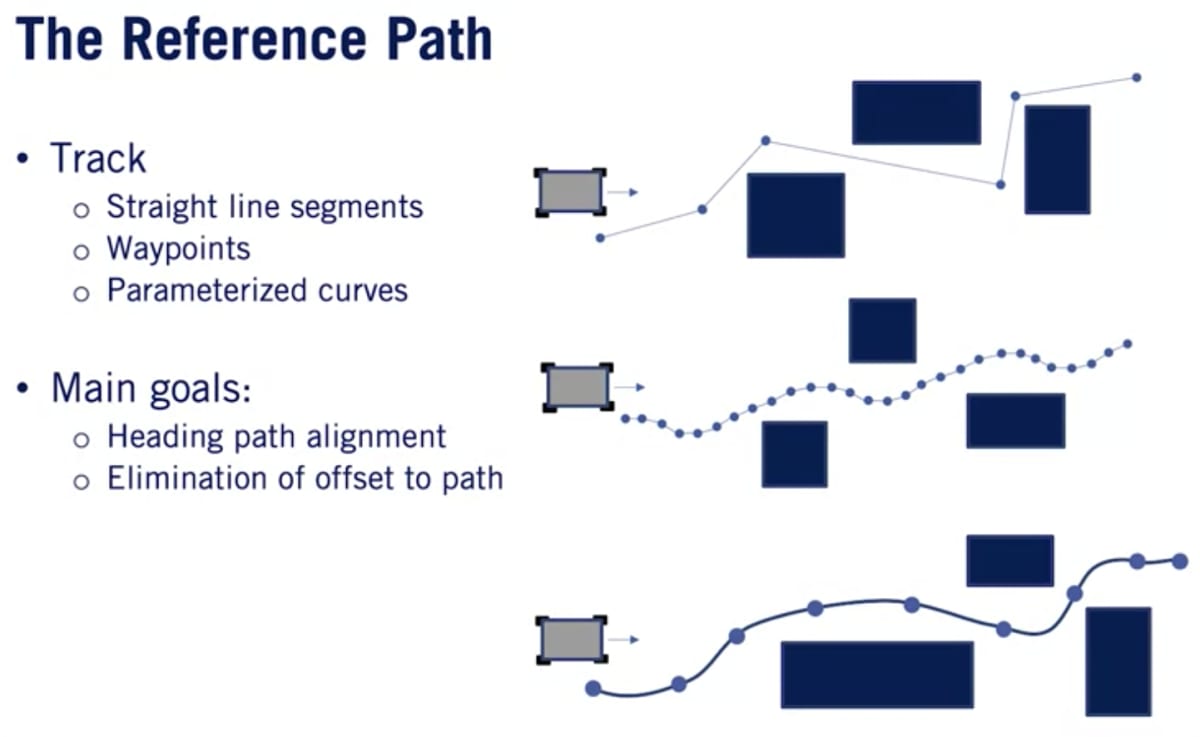
基準経路（Reference path）は横方向制御とPlanningシステムとのインターフェースで複数の方法で定義できる。

直線セグメント
- 一連の頂点群を直線接続する。コンパクトで構築が容易だが経路定義は不連続性が含まれるため、正確な追従が車両操縦の課題になる。
ウェイポイント
- 直線セグメントの改良版。距離または移動間隔で固定されたウェイポイントを使用する。操作が簡単で非常に一般的であり、特定ルートの事前走行により収集された状態推定値やGPSウェイポイントから構築できる。
パラメータ化された曲線
- 一連の固定モーションプリミティブから描画するかPlanning中の最適化を通じて生成できる。絶え間なく変化する動きを提供したり、滑らかな導関数を持つように構築することで一貫した誤差と誤差率の計算に寄与する。

全てのケースにおいて、コントローラーは車両と目的経路との間のオフセットを解消し、車両の向きを経路の向きに揃えようとする。

自動運転車で使用される横方向制御の主要カテゴリー

ジオメトリックコントローラー
- 目的経路の幾何学的特徴と座標および車両のkinematicモデルに依存する。
- 例：Pure Pursuit, Stanley
Dynamicコントローラー
- このカテゴリで最も一般的で高度なものはモデル予測コントローラー（MPC）。適用する制御コマンドを識別するため有限ホライズンの最適化を実行する。様々な制約に対応でき、現在の誤差以外を考慮して最適化できる。

自転車モデルの例とした誤差定義

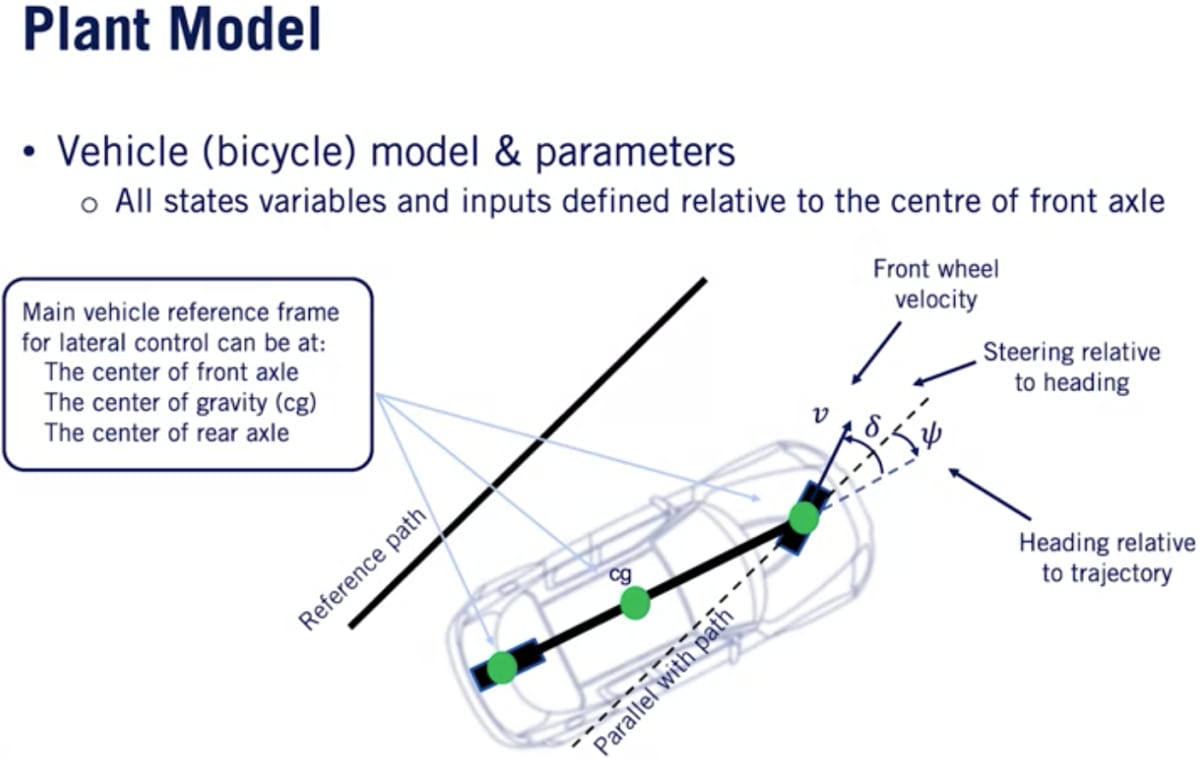
実線が基準経路で点線は基準経路と平行だが前車軸を通る線。

$ψ$ は経路直線に対する車両の相対方向角
$v$ は前輪の速度
$δ$ は車両の操舵角

コントローラーの設計に応じて基準フレームは後車軸、車両の重心にすることもできる。

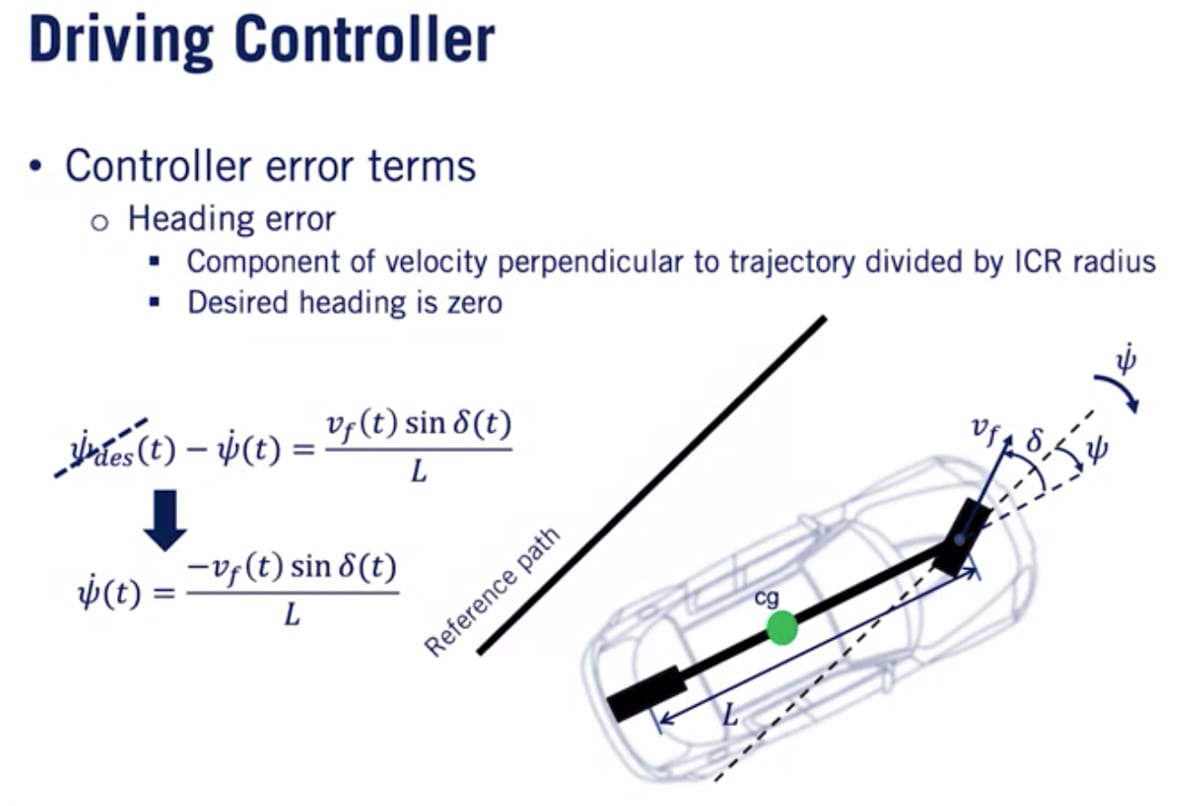
ヘディング誤差

ヘディング誤差は経路に沿った基準点における経路の向きと車両の向きとの差。車両がどれだけ経路の方向にどれだけ揃った向きで移動しているかの重要な尺度。ヘディング誤差率 $\overset{{.}}ψ$ によってヘディング誤差が時間と共にどのように変化するか理解できる。直線セグメントでは目的とするヘディング率 $\overset{{.}}ψ_{des}$ の変化はゼロになるため、 $\overset{{.}}ψ_{des}$ を削除することができる。

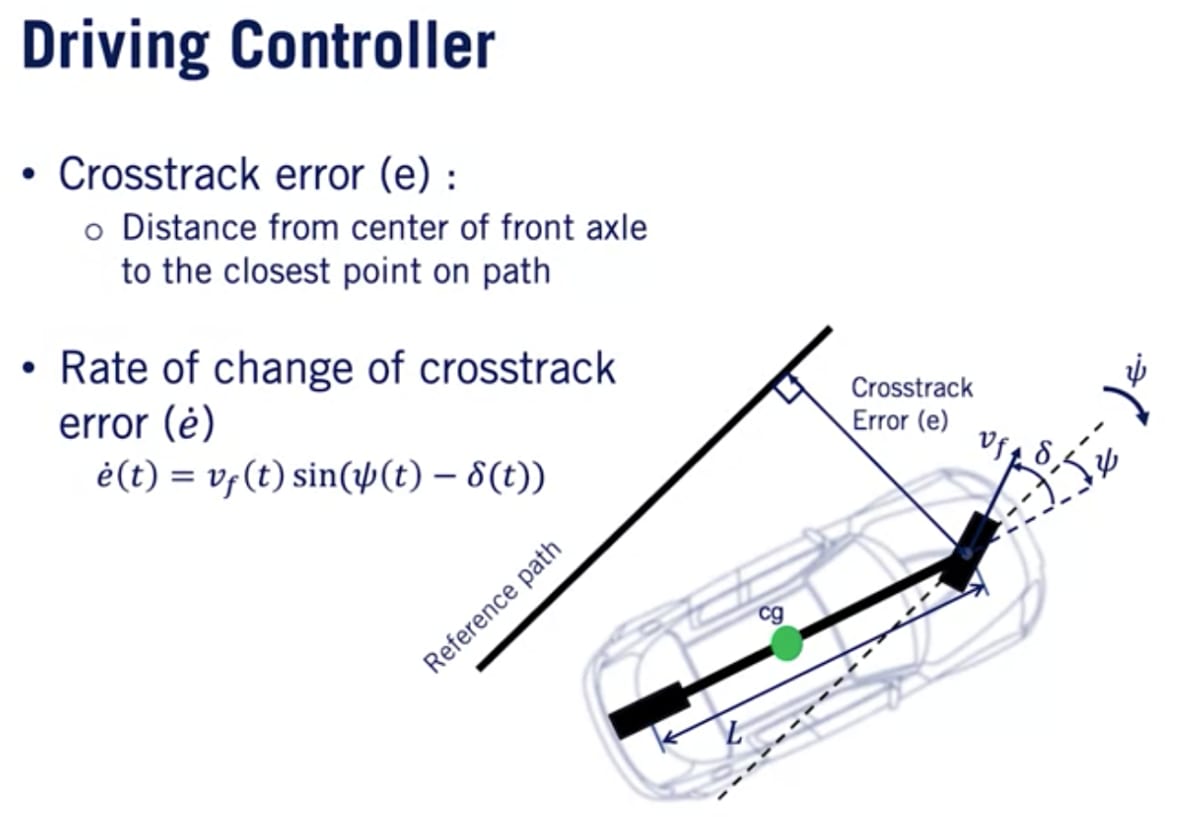
クロストラック誤差

オフセット誤差。車両上の基準点と目的の経路上で最も近い点との間の距離。車両の位置が経路上の望ましい位置にどれだけ近いかを示す主要な尺度。クロストラック誤差の変化率は前進速度の横方向の成分を抽出することで計算できる。速度が増加するにつれて誤差はより速く変化する（同程度の誤差を修正するためにより小さいステアリング角度で済む）。

湾曲した経路向けにヘディング誤差とクロストラック誤差を拡張するとさらに複雑さが増す（湾曲した経路との基準点をどこに配置するかすぐにわからないため）。

Lesson 2: Geometric Lateral Control - Pure Pursuit

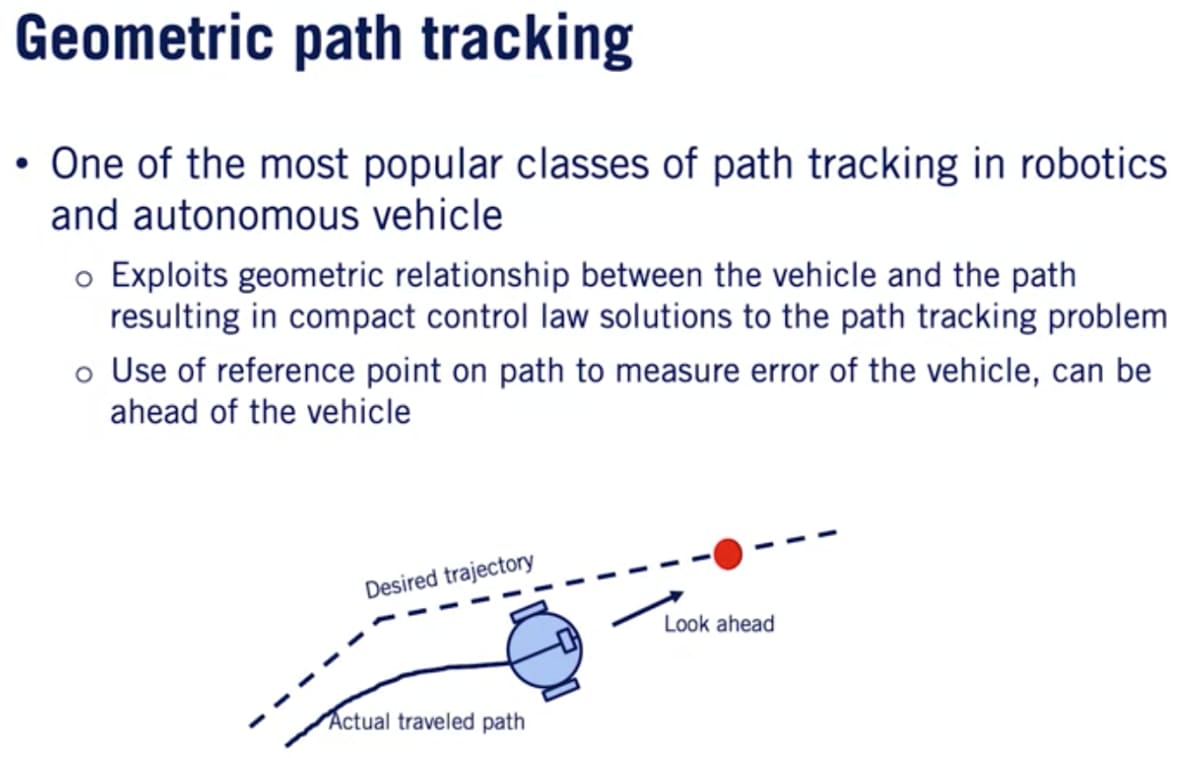
ジオメトリック（パストラッキング）コントローラーとは車両のkinematicsと基準経路の幾何学的特徴のみを使用して基準経路を追跡するコントローラー。

自動運転車の場合、ジオメトリックコントローラーは横方向コントローラーの一種で車両にかかるDynamicsを無視して車輪のスリップがない状態を仮定する。

シンプルなため、ロボット工学や自動運転で非常に一般的で有用。しかし、スリップなしの仮定に一致しない場合、パフォーマンスが低下する（例：高い横加速を伴うアグレッシブなステアリングなど）。これらの場合は複雑な制御戦略と利用可能なタイヤの力の限界を深く理解する必要がある。ただし、車両が線形タイヤ領域で動作していて飽和状態ではない場合、ジオメトリックコントローラーはうまく機能する。

ジオメトリックコントローラーは目的の経路上の基準点に依存する。これはヘディング誤差とクロストラック誤差の計算に使用される基準点か経路上の前方にある前方参照点（look-ahead point）になる。Pure Pursuit, Stanleyは前方参照点を利用して誤差を計算する。

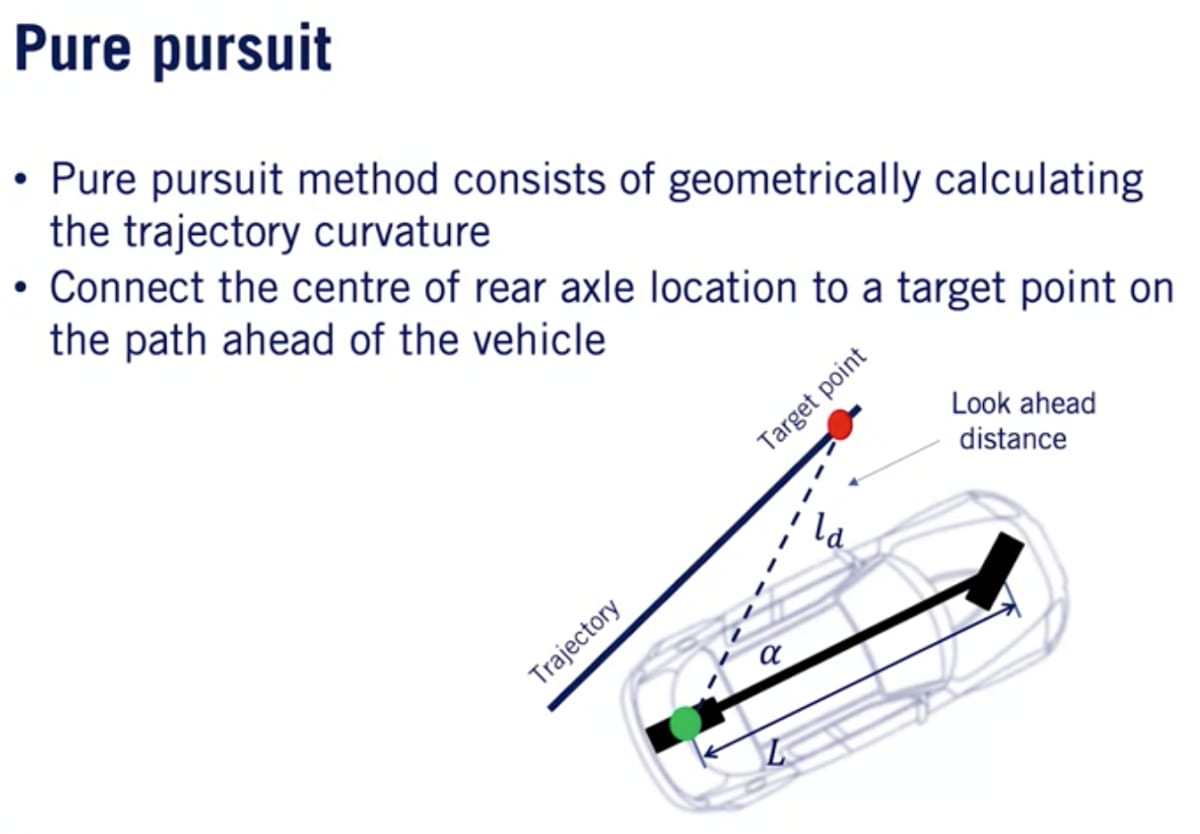
Pure Pursuitコントローラーの核となる考え方は基準点を車両の一定距離前方の経路に配置して、一定のステアリング角度でこの点と交差するために必要なステアリングコマンドを計算できること。経路曲線を辿るために車両が経路に向かってハンドルを切る際にポイントは前方に移動し続け、ステアリング角度は減りながら経路に徐々に近づいていく。

後車軸の中心を車両の基準点として参照する前方参照点をつなぐ線を前方参照距離 $l_{d}$ として定義する。車両の車体方向と前方参照距離との角度を $α$ とする。

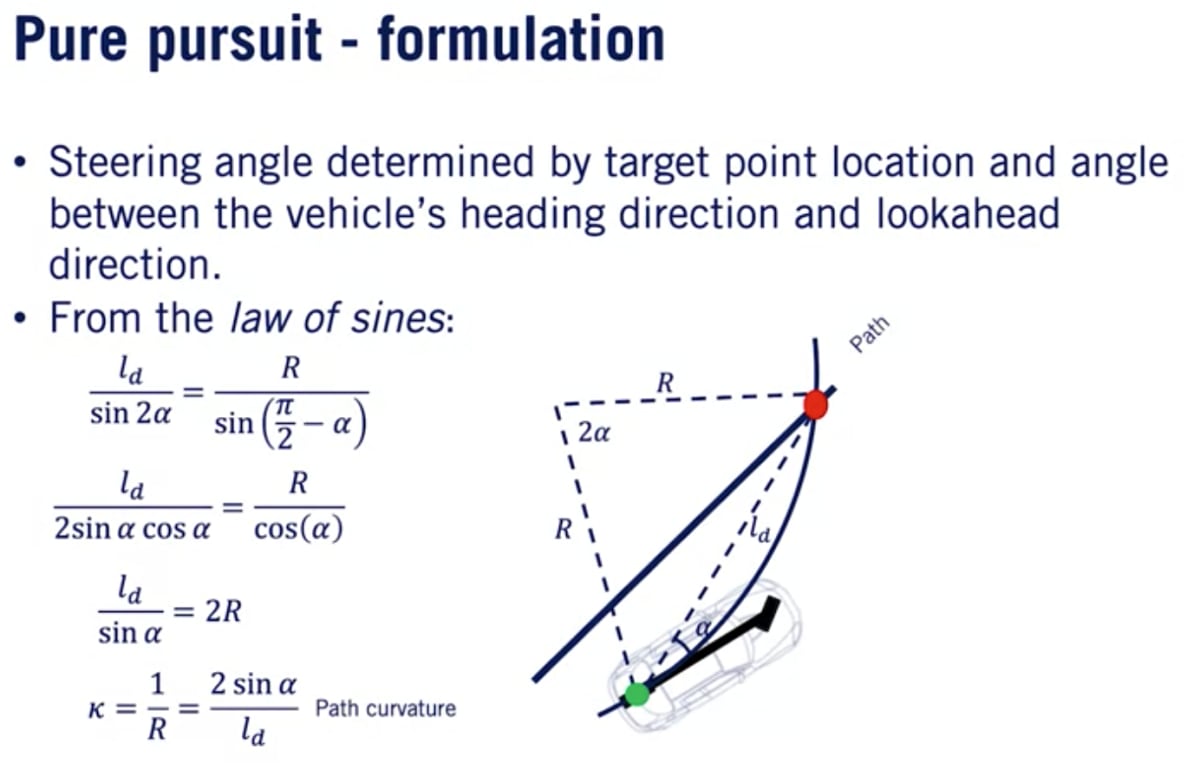
前方参照点と後車軸の中心とICR（瞬間回転角）は長さ $R$ の二つの辺と長さ $l_{d}$ の三角形を形成する。後車軸の中心を前方参照点とつなぐ円弧を定義するとこの弧はICR円の一部で $2α$ は三角関数から導出できる。 $κ$ は曲率。

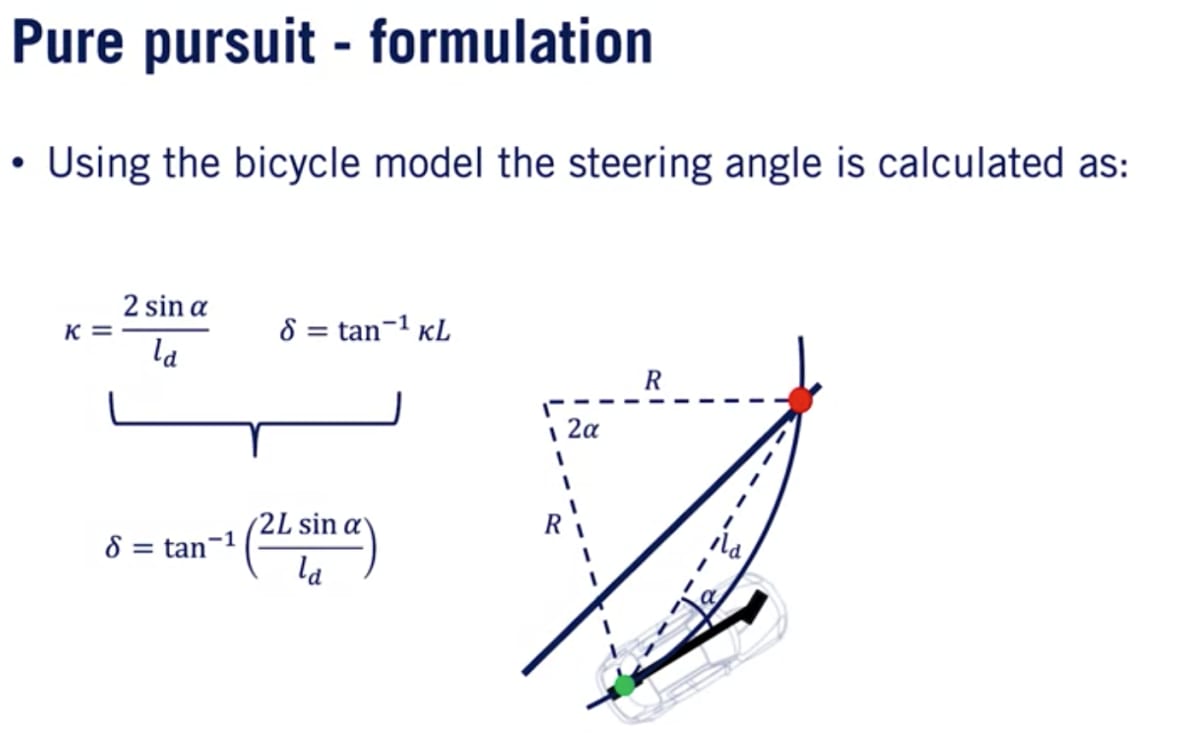
自転車モデルを使って、円弧の追跡に必要なステアリング角度を計算する。ステアリング角度 $δ$ は $tan^{-1}(\frac{2L \sin α}{l_{d}})$ となる。これは簡易実装のステアリングコントローラーとなる。

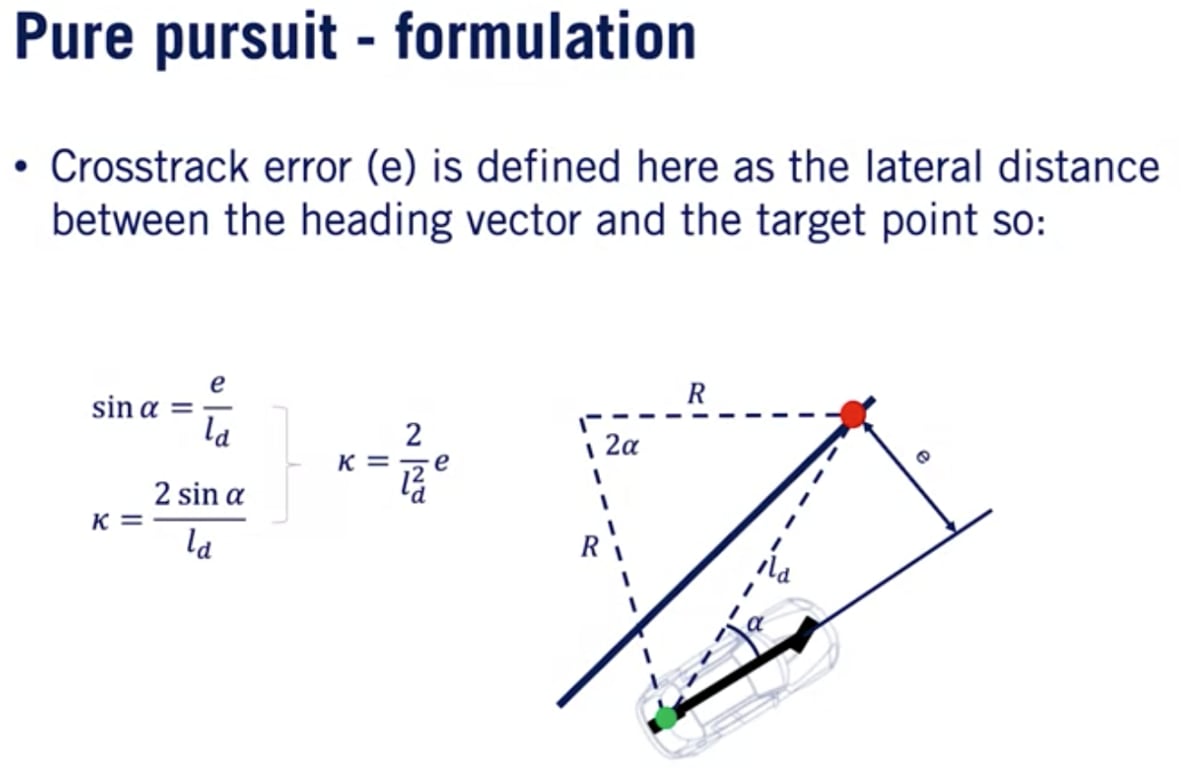
Pure Pursuitコントローラーの場合、クロストラック誤差 $e$ はヘディングベクトルと前方参照点との距離として定義できる。以下の式を組み合わせると経路の曲率は前方参照点でのクロストラック誤差に比例することがわかる。誤差が増加すると曲率が増加し、車両をより顕著に経路に戻す。

Pure Pursuitコントローラーは比例制御と同様の方法で動作し、コントローラーの出力としてパスの曲率を使用してクロストラック誤差を修正することになる。比例ゲインは $\frac{2}{l_{d}^2}$ に依存する。そのため、前方参照点が増加すると比例ゲインは非線形に減少する。また、固定値 $l_{d}$ のPure Pursuitコントローラーは速度を考慮しない曲率コントローラーとなることに注意する（時速10kmでも100kmでも同じステアリング角度になるため横加速度に著しい差が出る。高速用に調整されたコントローラーは低速で非常に遅くなり、低速用に調整されたコントローラーは高速で危険なほどアグレッシブになる）。

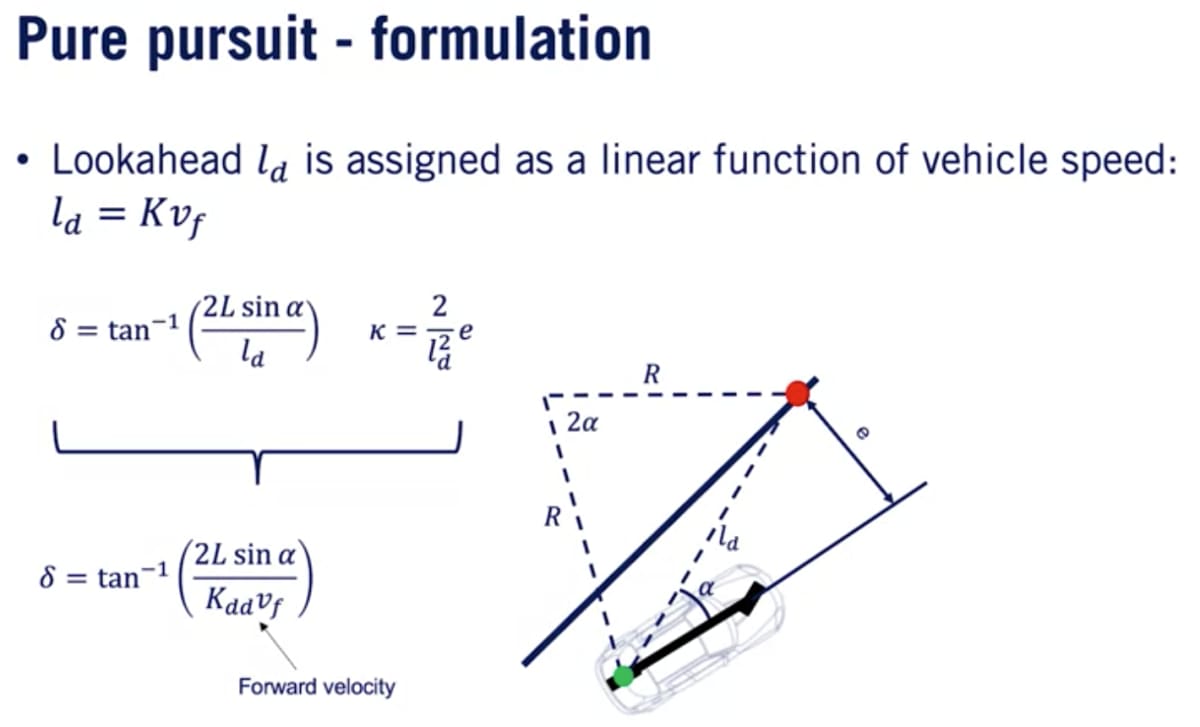
この問題を解決するために車両の速度に応じて $l_{d}$ を変更できるようにする。 $l_{d}$ は車両の前進速度に比例して増加するように定義する。 $l_{d}$ を $K$ （前方参照ゲイン）×前進速度 $v_{f}$ の形にして速度が速いほど前方参照点が遠くになるように調整する。この設計で利用可能なタイヤ力を考慮した達成可能なステアリングコマンドとターンレートが得られるがこれはそのように調整する必要がある。

Lesson 3: Geometric Lateral Control - Stanley

Stanleyはスタンフォード大学レーシングチームが第二回DARPA Grand Challengeで優勝した際に使用した（Stanleyはその時の車両の名前）。

主なアプローチ

車両基準点を後車軸ではなく、前車軸の中心に切り替えた。
前方基準距離なしでヘディング誤差とクロストラック誤差の両方を考慮する。
コントローラーの出力が最大ステアリング角度の制限内に収まるように制限した。

Stanleyコントローラーの3つのコンポーネント

経路に対するヘディング誤差を排除するためにステアリング角をヘディングに等しく設定する。
クロストラック誤差を排除するために比例制御を追加し、そのゲインは前進速度の逆数によって調整する。制御は逆タンジェント関数に渡され、そこでは比例制御信号が $-Π$ から $Π$ の角度範囲にマッピングされる。
ステアリング角度コマンドはステアリング角度の最小と最大である $δ_{min}$ から $δ_{max}$ におさまるように保たれる。

StanleyコントローラーはPure Pursuitコントローラーと同じ方法で前進速度によりゲインを調整し、さらに同様に比例制御信号の逆タンジェントを使う。

最終的な制御方法として、3つのコンポーネントを組み合わせてステアリング角度を設定する。

ヘディング誤差の場合、ステアリングコマンドはヘディング誤差とは反対の方向を指し、車両が方向転換して経路とのずれを修正する。大きなヘディング誤差の場合、ヘディング誤差がステアリング角度を超えるとコントローラーはアラインメントが有効な範囲内に戻るまで最大のステアリングコマンドを要求する。

大きなクロストラック誤差の場合、 $\frac{k_{e}}{v_{f}}$ は大きくなり、逆タンジェントは $\frac{Π}{2}$ に近づく。したがって、Stanleyコントローラーはヘディング誤差 $+\frac{Π}{2}$ で近似できる。この大きな値によってステアリングコマンドは最大になり、車両は経路に向かって旋回する。これによってヘディング誤差は反対方向に増加し、ヘディング誤差が $-\frac{Π}{2}$ に達するとステアリングコマンドはゼロに低下する。そして車両はクロストラック誤差が減少するまで経路に直進する。この時点でヘディング項が再び経路とのアラインメントの修正を開始し、最終的に車両はより厳密に経路に追従し始める。

Stanleyコントローラーの収束特性について、前車軸が基準点のクロストラック誤差に制限なくStanley制御を代入すると最終方程式が得られる。

小さなクロストラック誤差の場合、2次項が無視できると仮定するとクロストラック誤差は1階の微分方程式に従うことになり、ODE解は指数関数になる。 $k$ は正であるため、誤差は指数関数的に0に減衰する。また、減衰率は速度に完全に依存しておらず、高速の車両は経路に収束しながらより遠くまで移動するが、低速の車両と同時にパスに収束する。

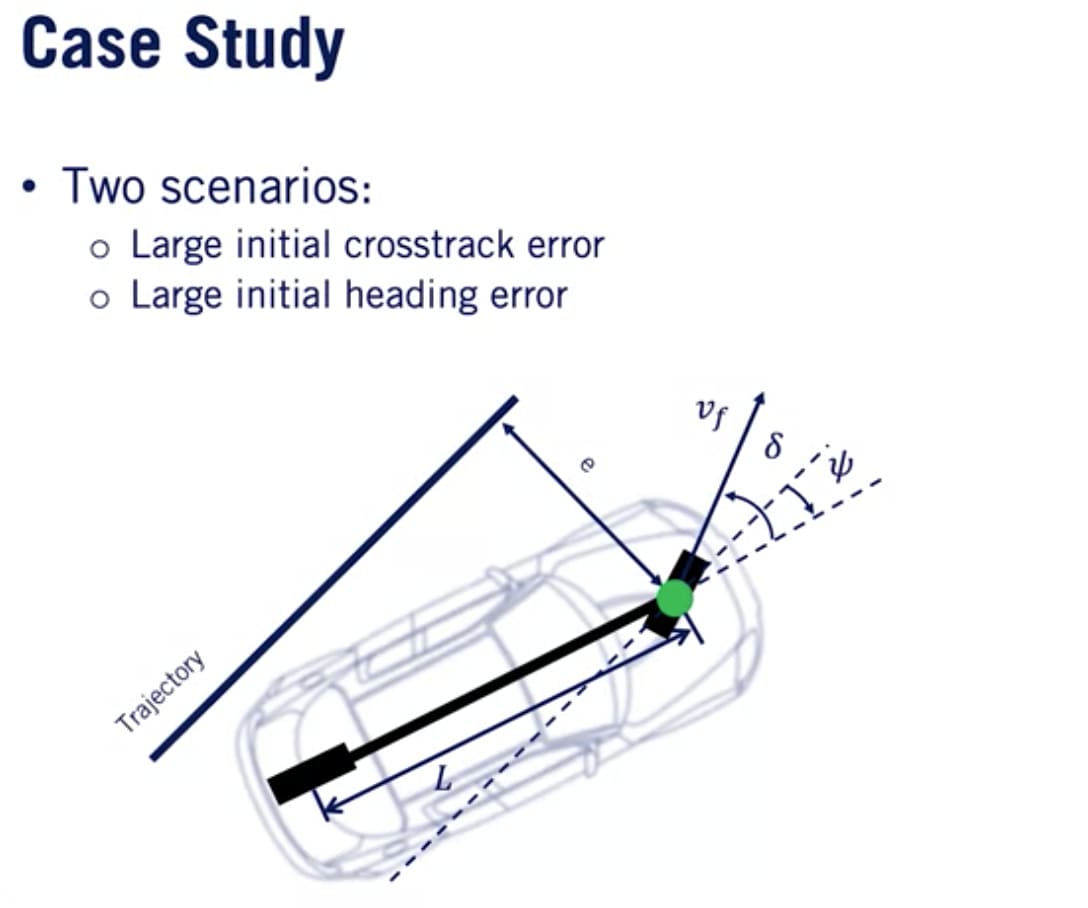
2つの極端なシナリオで収束特性を観察する。

大きな初期クロストラック誤差
大きな初期ヘディング誤差

大きな初期クロストラック誤差

初期条件としてクロストラック誤差5mの他、以下を仮定する（シミュレーション用に選択されたパラメータおよび試行錯誤テストによって選択された）。

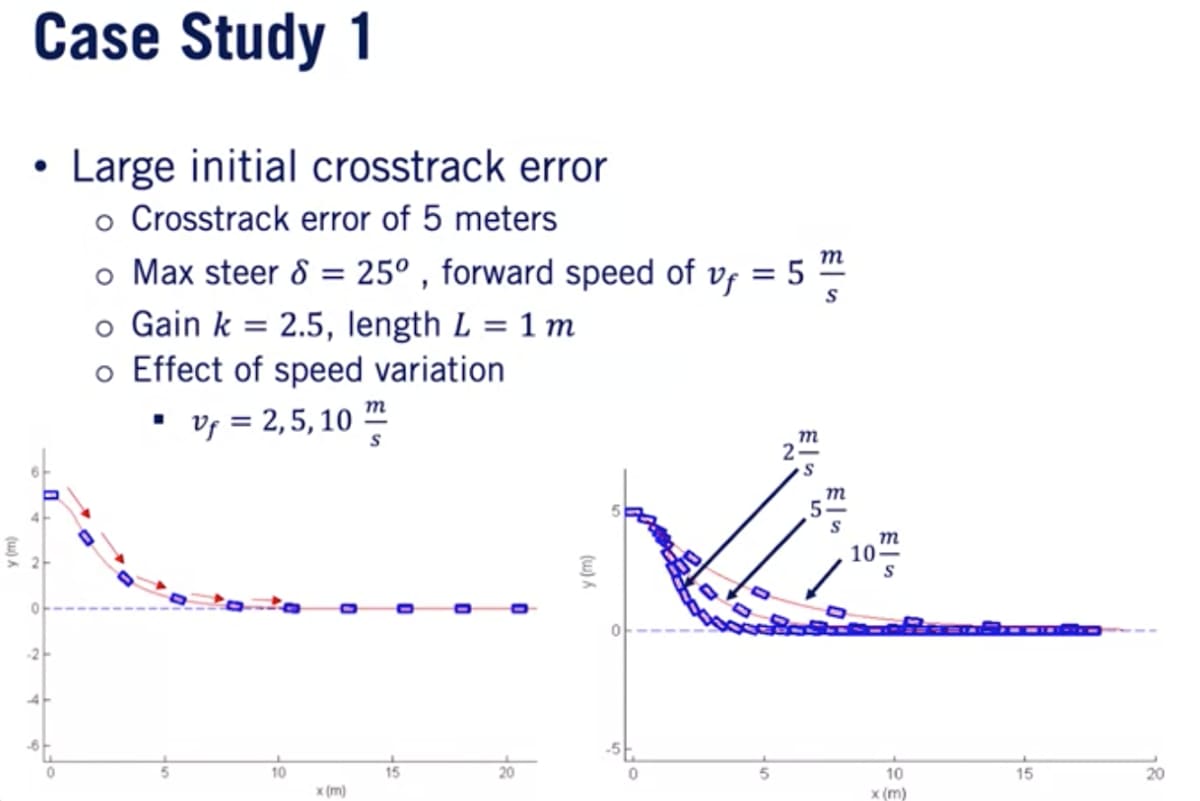
大きな初期クロストラック誤差は車両を素早く経路に向けさせる大きなステアリングコマンドに繋がっている。また、速度が速いほど経路に到達するまでにより遠くに移動する（小さなクロストラック誤差では最終収束にかかる時間は同じになる）。

大きな初期ヘディング誤差

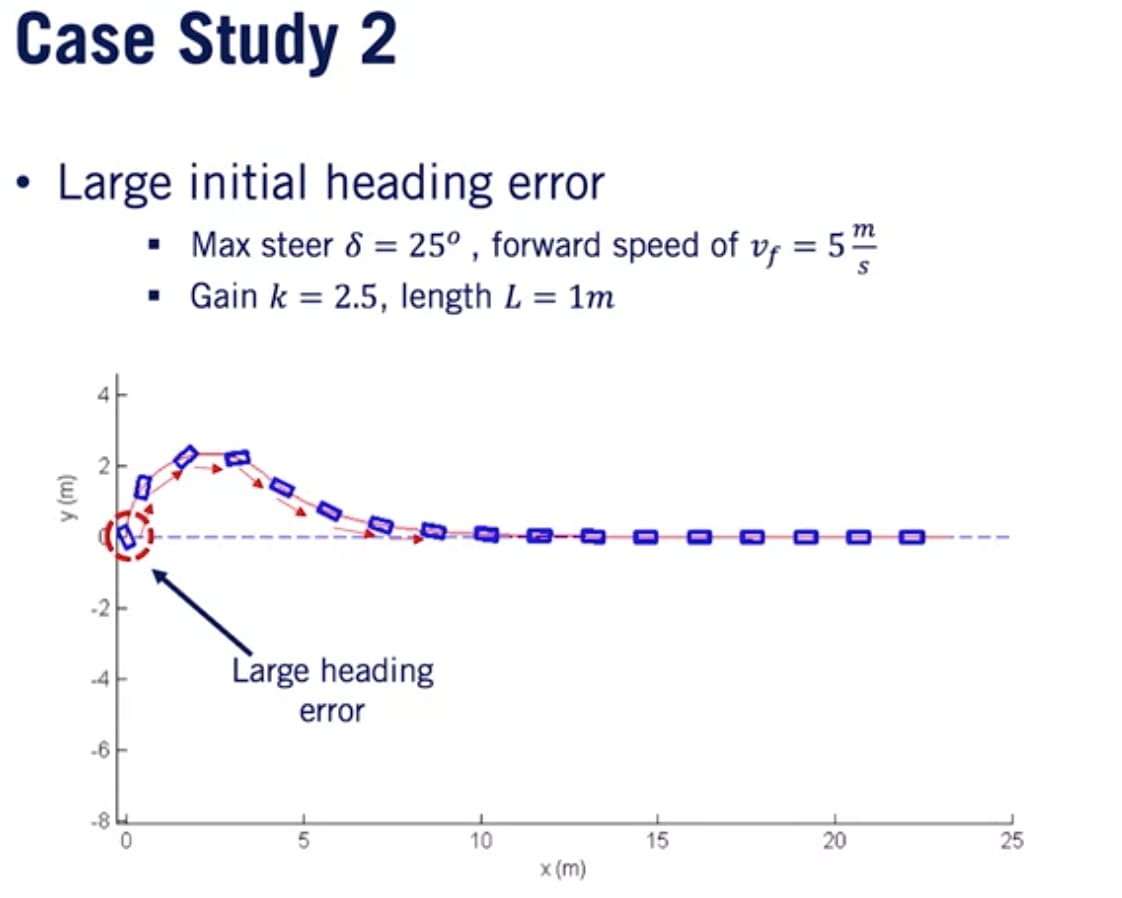
車両は著しく誤った方向を向いて始まる。シミュレーション結果はヘディング誤差はStanleyコントローラーによって修正されている。まず、ヘディング誤差が修正されるようステアリングコマンドが制限値に達し、次にクロストラック誤差が増大し始めるとステアリングコマンドは経路とのアラインメント状態を超えて車の方向を修正し続ける。最後に車は大きな初期クロストラック誤差のケースと同じように収束段階に入っていく。

これらのシミュレーション結果はStanleyコントローラーが任意の大きば誤差を修正する能力を証明しており、実際にグローバルな安定性が保証される（初期状態がどうであってもコントローラーは車を経路に戻す）。

しかし実際は、Stanleyコントローラーはジオメトリックコントローラーであり、自動運転車の多くの異なる側面を考慮していない。例としてノイズの多い測定、アクチュエーターのDynamics、タイヤの力の影響など。これらは運転中の不快な乗り心地を引き起こす可能性がある。

これらの影響の一部を軽減するためにジオメトリックコントローラーに調整を加えることは可能で以下のようなアプローチがある。

Lesson 4: Advanced Steering Control - MPC

MPCは各タイムステップで最適化問題を数値的に解決する制御設計アプローチ。各タイムステップでの最適化は時間がかかるため工業用化学処理などの低速プロセスに適用されていた。しかし、ハードウェアの性能向上により組み込みハードウェア上でも実行可能なアプローチになった。また、MPCは後退ホライズン制御（Receding Horizon control）とも呼ばれる。

MPCの利点

定式化が簡単。目的関数の定義と関連する制約を用意し、ソルバーで最適化できる。
状態と制御信号が安全な動作範囲にとどまるように制約でき、複数の目的を同時に最大化するように制御を選択できる。
線形、非線形モデルに適用できる。

MPCの短所

静的制御よりはるかに多くの計算リソースを必要とする。プロセッサの過負荷を避けるために慎重に実装する必要がある。

後退ホライズン制御（Receding Horizon control）

後退ホライズン制御は各タイムステップで固定サイズの最適化を行う。実装で発生する問題は最適化に時間がかかるため、最適化開始時と完了時の車両の状態が異なること。結果として制御入力が実際に適用される時点の最適化では予測状態を使用する必要がある。

車両が現在の状態 $x_{t-1}$ から $x_{t}$ へ移動する間に最適化を実行するが外乱のため時刻 $t$ の予測状態へ正確に到達するとは期待できない。しかし時間間隔が短い場合はかなり近いと期待できる。

MPCアルゴリズム

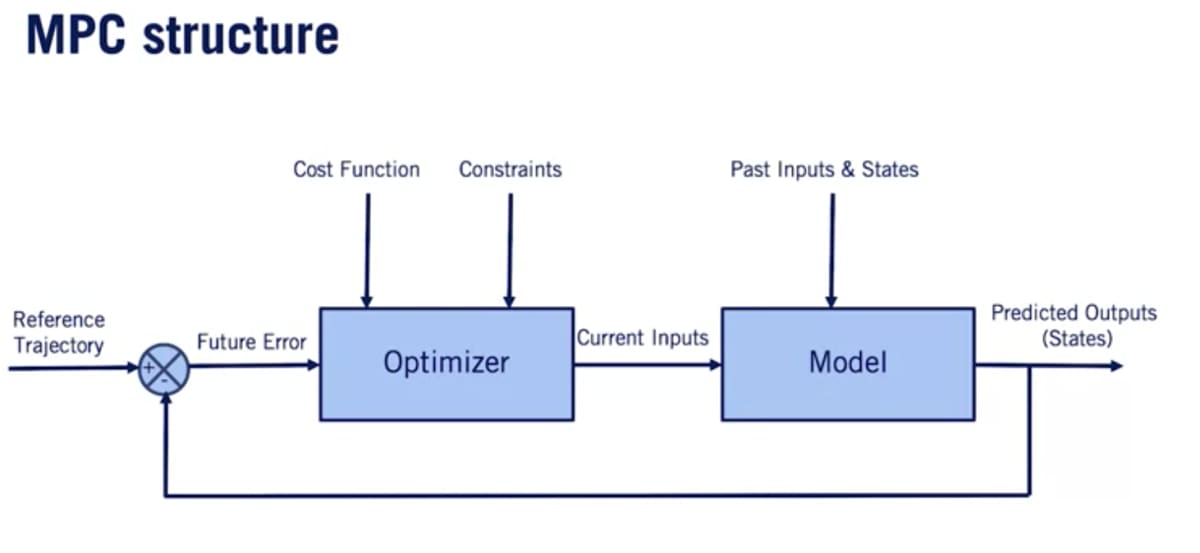
モデルはt-1から過去の入力と状態を受け取る。
オプティマイザーから現時点における時間区間の各タイムステップでの入力シーケンスを取得する。
モデルは次のタイムステップでの予測状態を出力する。これは基準軌道と比較され、将来または予測される誤差としてオプティマイザーに渡される。
オプティマイザーは使用する制約とコスト関数の更新も受けとる（これらは事前に確定しておくか動作モードの変更に基づいて可変にできる）。
オプティマイザーで最適化を実行する

以上のプロセスを繰り返す。

線形MPC

将来の状態は現在の状態とアクチュエータ信号に線形的に関連。 $A$ と $B$ は係数行列で時不変を仮定する。
MPCは有限の時間区間にわたっての入力制御ポリシー $U$ を探す。

すべての状態をゼロに駆動する場合、最小化する際の目的関数またはコスト関数はゼロからの状態と非ゼロの制御入力の両方の偏差の二乗誤差。これは最適制御理論の最適化問題に似ており、制御パフォーマンスと入力の激しさとの間のトレードオフとなる。行列 $Q$ と $R$ は重み行列と呼ばれ、特定タイプのレスポンスを達成するために選択できる。

基準軌道などの目的の信号を追跡する必要がある場合、目的の状態に対する誤差 $δ_{x}$ を含めるように定式を変更する。

これは有名な最適化定式で、閉形式のソリューションを持つLQR（線形二次レギュレーター）である。
閉形式ソリューションでは、すべての状態が制御レスポンスで使用される。LQRは制御ゲイン行列 $K$ を定義する。これは状態空間モデルの $A$ と $B$ 行列、コスト関数の $Q$ と $R$ 行列から計算できる。

非線形MPC

非線形関数の最適化に課せられる制約には次のものが含まれる。モーション、状態、最大のステアリング角度などを捉える入力境界の非線形Dynamicモデル、システムに影響を与える他の不等式制約 $g$ や等式制約 $h$ など。
しかし、このような最適化問題の場合、閉形式のソリューションは存在しない。そのため、ソリューションを見つけるには数値最適化に頼らなければいけない。Kinematic自転車モデルでさえこのカテゴリーに分類される。従って、自動運転用のほぼすべてのMPCコントローラーは数値的に最適化する必要がある。

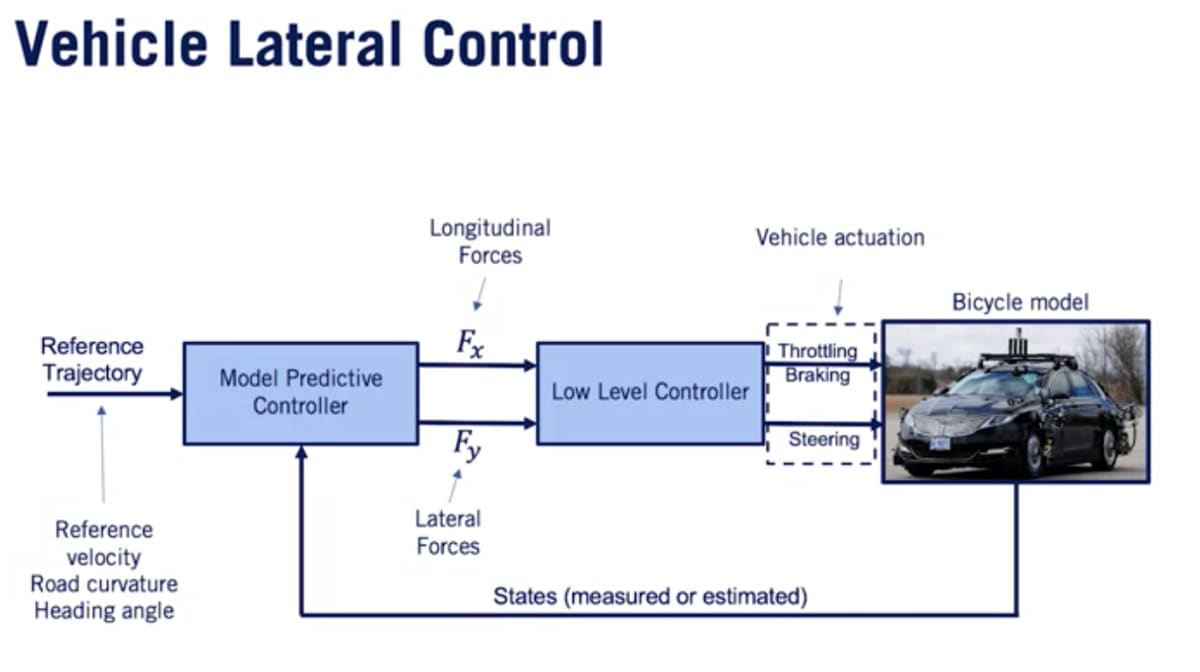
MPCはフィードバック構造で使用されるが、タイヤ力からスロットル、ブレーキ、ステアリングコマンドへの変換は低レベルコントローラーに含める。

MPCブロックへの入力は基準軌跡でこれには基準経路、速度、各タイムステップでの車両状態が含まれる。
MPCブロックの出力は目的の軌道に追従するために必要な横方向・縦方向の力でこれらの力はスロットル、ブレーキング、ステアリングコマンドに変換される。

最後に各タイムステップでアクチュエーション信号が車両に適用され、新しい車両状態に到達してフィードバックループが閉じる。

二重のレーン変更を操縦する場合、MPC最適化は次のように設定する。

目標軌道を追跡するコスト関数を定義する。
- 目標軌道からの偏差と制御コマンドの振幅の最小化が含まれる。
車両のモーション制約を定義する。
- 縦方向・横方向のDynamicモデルに依存
- エラー制御における極端な反応を回避するためにタイヤの力に上限の制約を課してタイヤが線形タイヤ領域内に入るように制限する。
これらのコスト関数と制約によって、この例で使用される最適化が定義され、低レベルコントローラーによって実際の車両コマンドに変換される。
- 低レベル制御をMPC最適化に組み込むことは可能で、これにはエンジンマップ、完全な車両のDynamicモデル、アクチュエーターの力のモデル、タイヤの力のモデルを制約に含める必要がある。結果はリアルタイムで解決するのが難しい可能性がある大きな最適化問題になる。

シミュレーション

車両が時速60kmの定常速度まで加速し、次に左に4m移動し、その後すぐに右に4m戻る二重レーン変更シナリオの例。

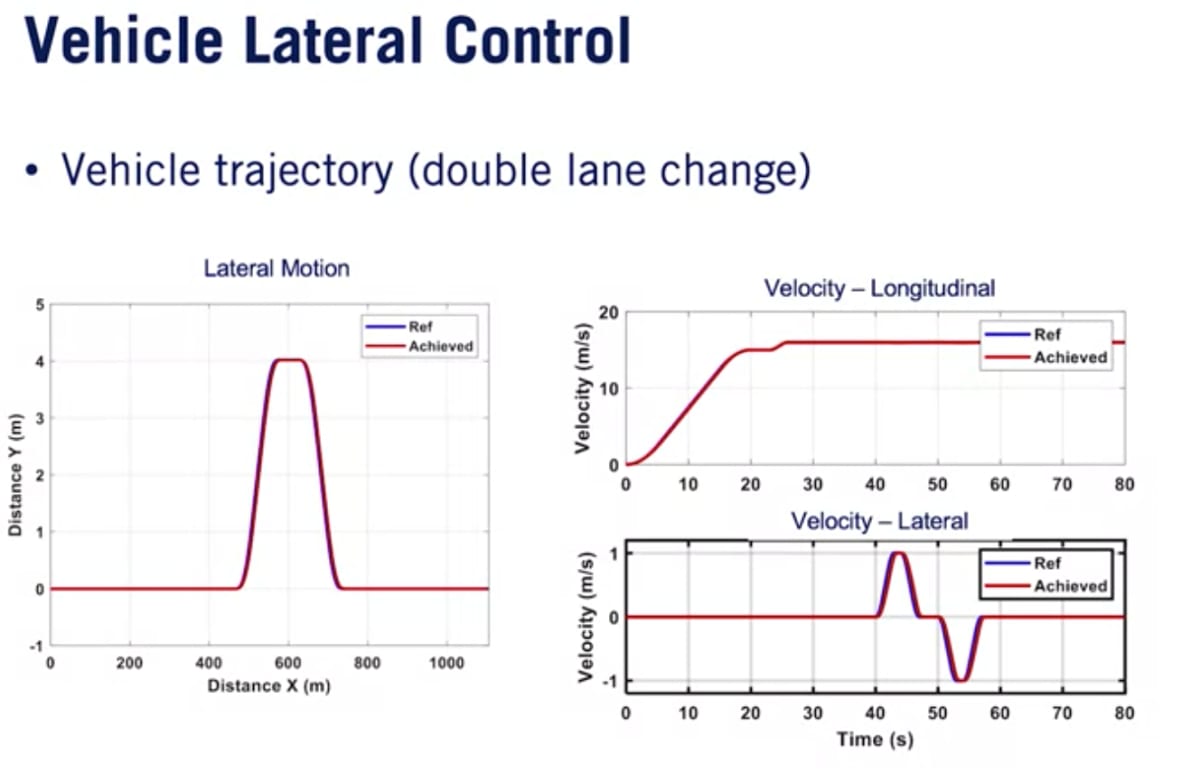
MPCコントローラーの追従は優れており、わずかに遅れているが、オーバーシュートや振動はない。これはシミュレーションとMPCは同じモデルとパラメータを使用しているため驚くことではない。

MPCコントローラーの出力である縦方向・横方向の力は滑らかに変化し、適切に動作している。また二重レーン変更中の車両のヨーレートを見ても正確に追跡できている。

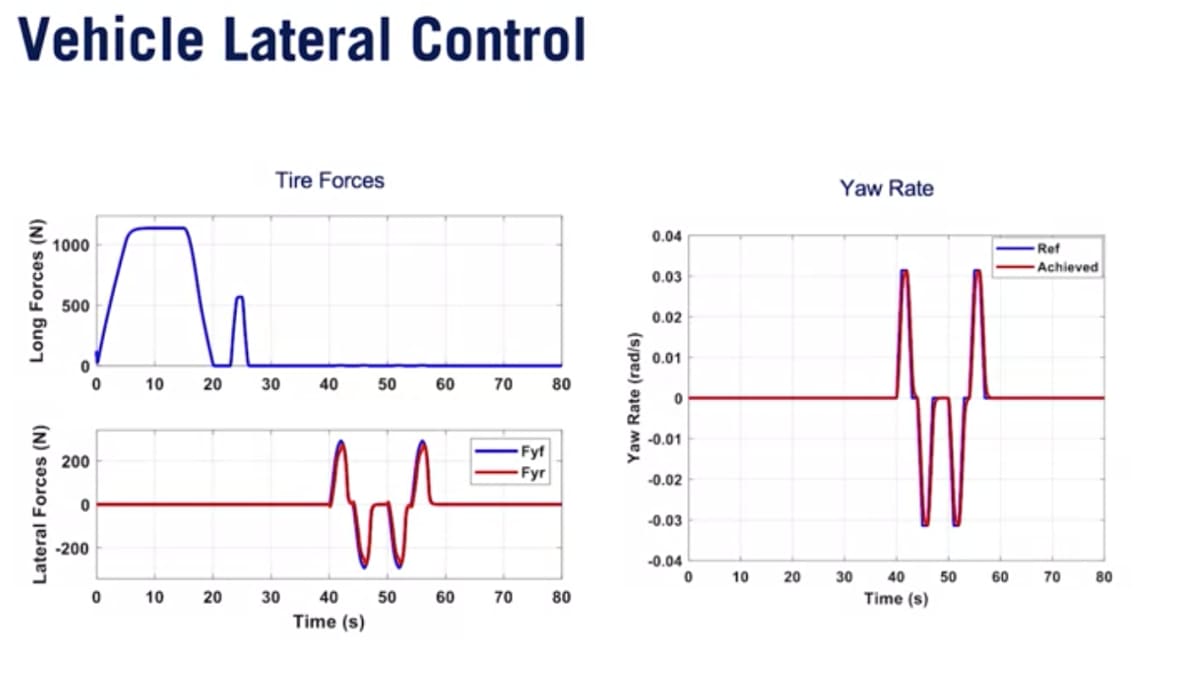
MPCは自動運転のための制御技術として多くの可能性を示していて、幅広い動作条件と多種多様なシナリオに対して変更なしで使用できる。この柔軟性と利便性は、計算要件の増加を犠牲にして実現され、利用可能な時間枠内で実行可能な解を常に返す堅牢な最適化ソルバーの可用性に依存している。

Week6はこれにて終了。
Week7はこちら