はじめに
https://zenn.dev/asap/articles/2269cd74c5ddc2
先日、分散共分散行列についての魅力を思いのままに殴り書きしたポエムを公開しましたが、その中で主成分分析(PCA)に関しては、最後に雑に触れただけでした。
今回は主成分分析に絞って、どういう流れで、「分散共分散行列の固有値問題を解くこと」=「主成分分析」となったのかを数式で1から説明できればと思います。
1軸目だけでなく、k軸に一般化して最後まで説明している記事はあまりないと思うので、参考になれば幸いです。
主に下記の動画・書籍を参考にしました。
特に下の書籍は、線形代数の解説の中で行列から主成分分析・ラグランジュの未定乗数法などまで、今回の記事で利用している道具のほとんどを勉強することができるため、おすすめです!
主成分分析(PCA)の気持ち
妥協しないデータ分析のための 微積分+線形代数入門
主成分分析とは
主成分分析(PCA,Principal Component Analysis)は、次元削減技術の一つです。
次元を削減するということは、例えば2次元で表現されるようなデータを1次元で表現することになるので、基本的に情報が失われます。
この時に失われる情報を最小限に抑えて、なるべく多くの情報を保持したまま、次元を削減するための技術になります。
次元を削減することで、データ分析や機械学習において扱いやすくなるため、重宝されている技術になります。
導出
では、主成分分析を導出してみたいと思います。
はじめは、2次元のデータから1次元のデータに圧縮することを考えます。
軸となるアイデアは、「失われる情報を最小限にする」です。
「分散を最大にする方向に軸を引く」の説明

例えば、上記のようなデータの分布を考えます。
データの意味はなんでも良いです。例えば今回は横軸に身長、縦軸に体重とでもみなしましょう。
(横軸をx軸、縦軸をy軸とします)
そうすると、ある14名の(身長,体重)のペアをプロットしたデータになります。
上記のデータを見ると身長が高くなるほど、体重が高くなるような相関のある分布になります。
ここで例えば、下記の赤線のような軸を追加することを考えます。この軸をz軸と呼びます。
続いて、主成分分析では、2次元のデータを1次元に圧縮するために、圧縮先の次元の軸を考えます。
このとき、下記の画像の赤線のように、データの重心(平均)の位置を通る、z軸を考えることができ、2次元のデータを1次元に圧縮するというのは、追加したz軸にデータ点から垂線を下ろした点が、次元削減後の点になることがわかると思います。
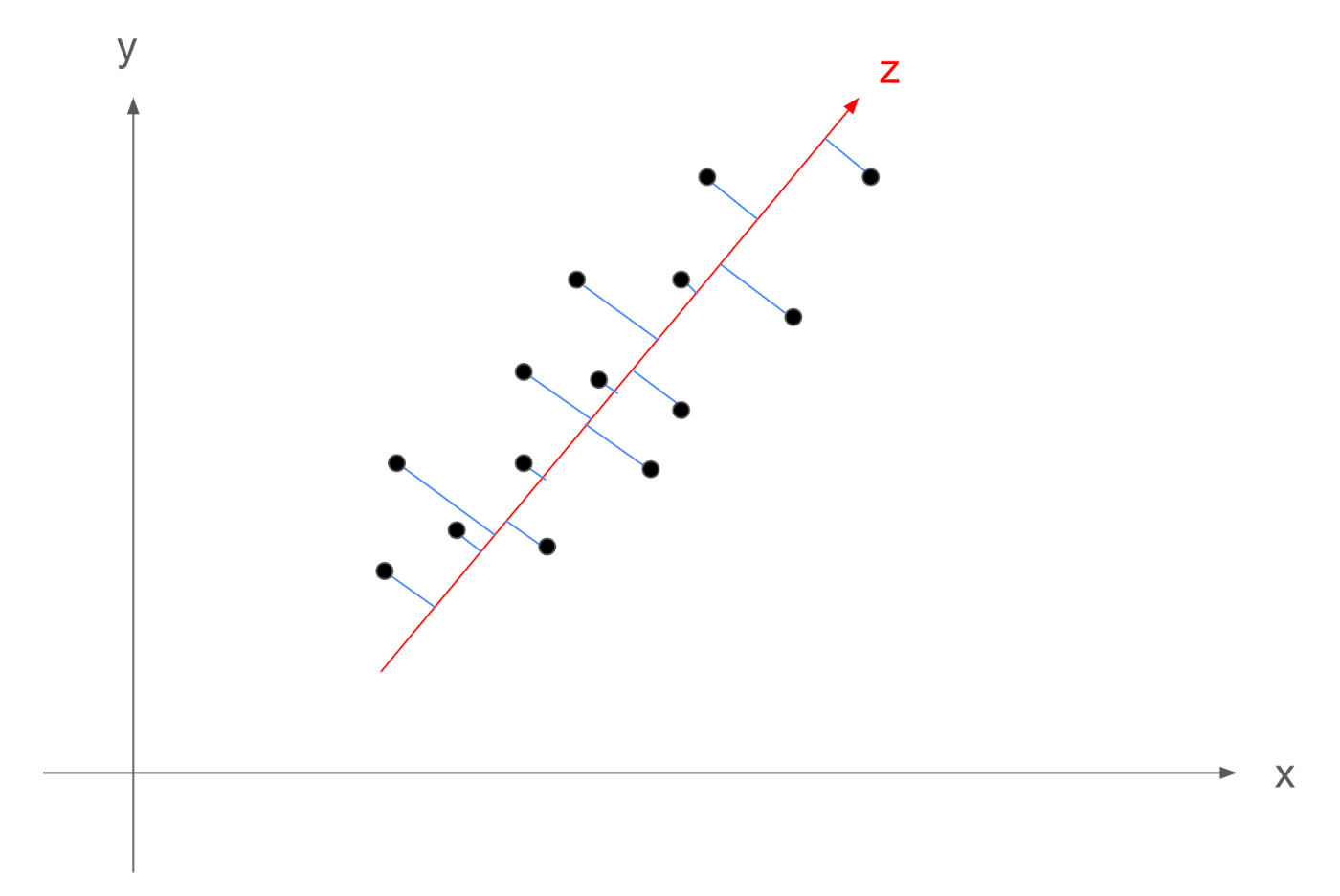
では、どういうz軸を引けば、次元削減後に「失われる情報を最小限にする」ことができるでしょうか。
ここで、ある1点のデータ点とz軸、前データの平均点に着目すると、下記の図のような関係を考えることができます。

図中の赤点は、全データ(14点)の平均(重心)を表します。
(逆にいうと、z軸は重心を通る軸です)
すると、重心とデータ点とz軸上の次元削減後の点は直角三角形を作るので、三平方の定理が成り立ちます。
今回は、ある一つの点に対して、注目しましたが、上記の関係性はすべてのデータ点にて成立するため、下記が成立するはずです
\frac{1}{N} \sum_{i=1}^{N} c_i^2 = \frac{1}{N} \sum_{i=1}^{N} a_i^2 + \frac{1}{N} \sum_{i=1}^{N} b_i^2
ここでNはサンプルサイズであり、上の図の例ではN=14です。
ここで、c_iは、標本平均とサンプルとの距離になるため、z軸をどうひくかに影響されず、常に一定の値になります。
続いて、b_iは「次元削減後に失われる情報」になります。
次元削減後はz軸上のデータの位置の情報しか持たないため、z軸と直行する成分は失われます。
したがって、この\sum_{i=1}^{N} b_i^2を可能な限り最小にすることで、次元削減後に「失われる情報を最小限にする」ことができます。
そうするには、c_iが固定なので、\frac{1}{N} \sum_{i=1}^{N}a_i^2を最大化する必要があります。
\frac{1}{N} \sum_{i=1}^{n} a_i^2というのは、次元削減後のサンプル点と全サンプルの重心(平均)との距離の2乗の平均になります。
数式で書くと下記のようになります。
\frac{1}{N} \sum_{i=1}^{n} a_i^2 = \frac{1}{N} \sum_{i=1}^{14} (X_i - \bar{X})^2
ただし、X_iはデータ点、\bar{X}はデータ点の平均を示します。
これは、標本分散の定義式と一致します。
つまり、次元削減後に失われる情報を最小限にするためには、次元削減後のデータの分散が最大になるようにz軸を引けば良いことがわかります。
式変形(準備)
記号の導入
では、分散を最大化する方向のベクトルを数式で求めていきます。
そのための準備として、数式で取り扱えるように、図に対して文字をおいていきます。
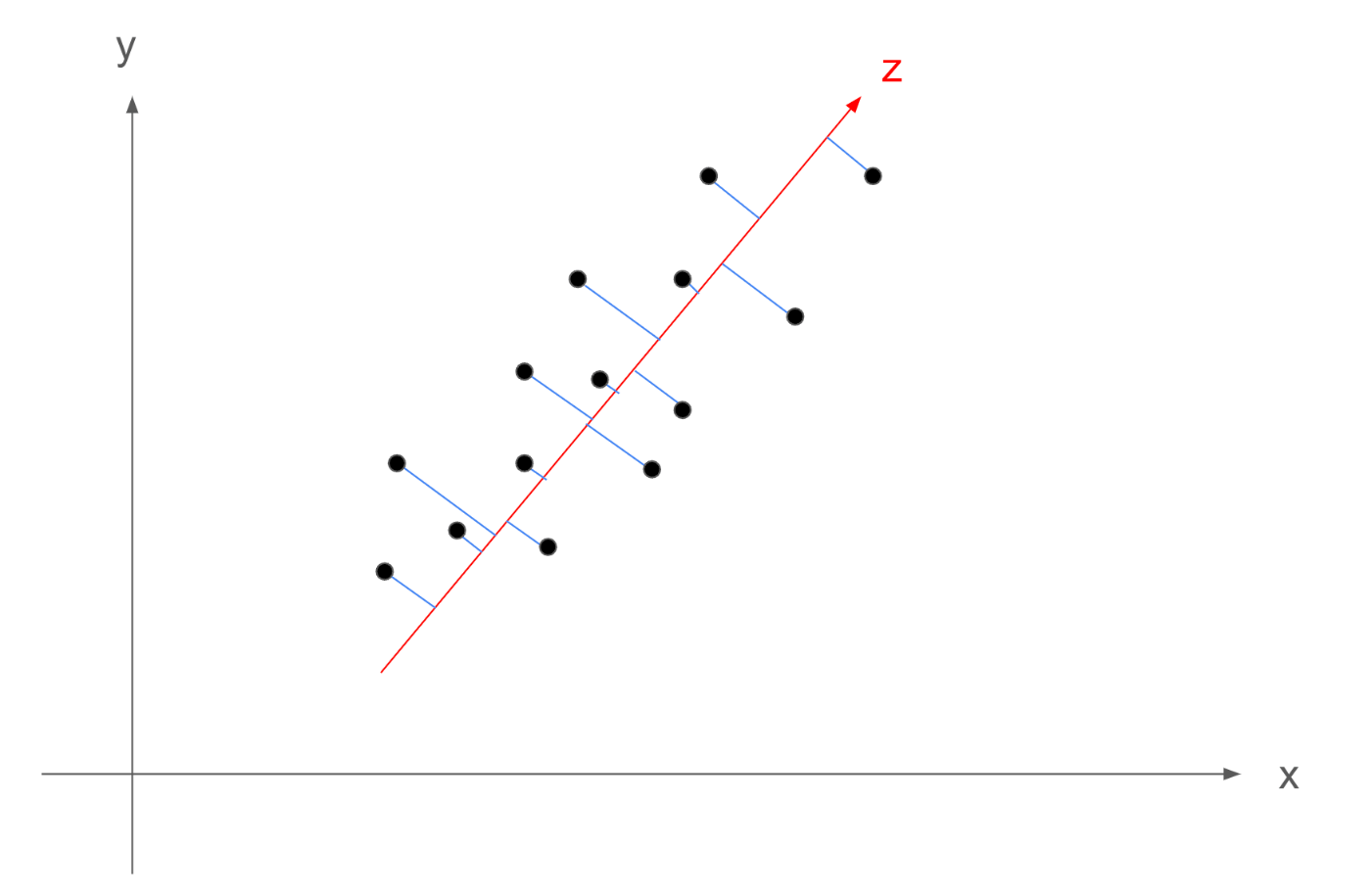
まず、各データ点は下記のように表します。
S=\{X_1,X_2,......,X_{14}\}
加えて、それぞれの要素はさらに下記のようなベクトルを表します。
X_i =
\begin{pmatrix}
x_i \\
y_i
\end{pmatrix}
また、各次元ごとの要素の集合を下記のように定義する
X'=\{x_1,x_2,......,x_{14}\}
Y'=\{y_1,y_2,......,y_{14}\}
さらに、次元削減に利用するz軸の基底ベクトルをvとします。
vは下記の要素を持ち、このvを見つけることが目標です。
v =
\begin{pmatrix}
x_v \\
y_v
\end{pmatrix}
また、次元削減後のデータ点を下記のように表します。
R=\{Z_1,Z_2,......,Z_{14}\}
各要素は、xy平面上で、下記の要素を持ちます。
Z_i =
\begin{pmatrix}
z_{ix} \\
z_{iy}
\end{pmatrix}
中央化
続いて、これまで記載されていたデータの分布を下記のように並行移動して、重心を原点に持ってきます。
これを中央化といい、データの平均が原点になります。
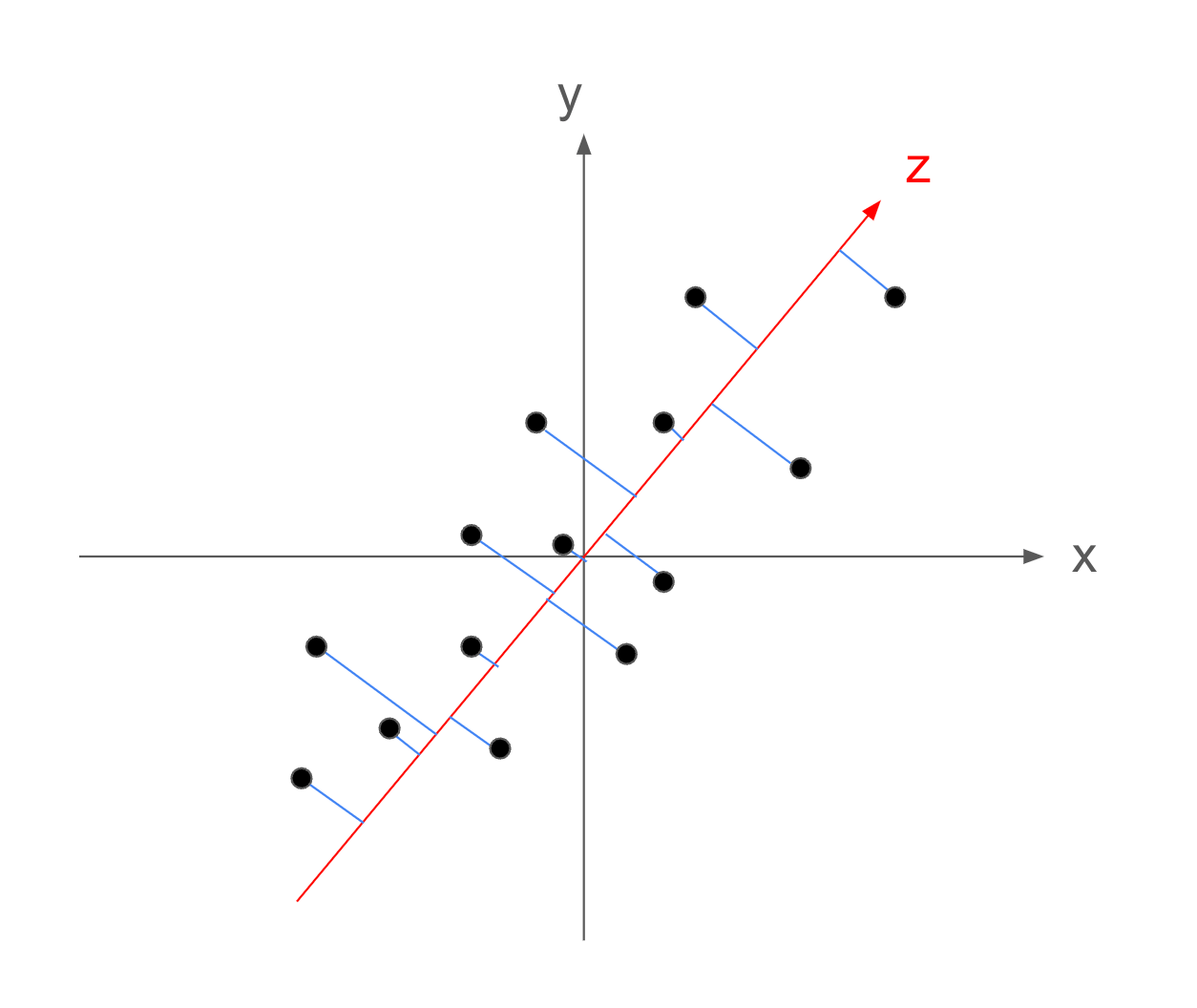
このとき、データの平均が原点であるという条件を付け加えることで、変換前と同値な書き換えになります。
このように変換することで、最大化したい分散を平均からの距離ではなく、原点からの距離として考えることができるので、計算が簡単になります。
式変形(1軸目を考える)
vを含む式に変形する
では、実際に式変形をしていきます。最大化したいのは分散なので下記の形からスタートしていきます。
まずは、求める分散は、中央化により、次元削減後の点Z_iと原点との距離とかけるので下記のようになります。
\frac{1}{N} \sum_{i=1}^{N} a_i^2 = \frac{1}{N} \sum_{i=1}^{N} Z_i^2
続いて、次元削減後の点Z_iは次元削減前の点X_iを、z軸の基底ベクトルvに正射影したものになるので、条件として\lvert v \rvert ^2 = 1を加えると、Z_iはvとX_iの内積として考えられるため、下記のように変形できます。
\frac{1}{N} \sum_{i=1}^{N} Z_i^2
= \frac{1}{N} \sum_{i=1}^{N} (X_i^t v)^2
ここからは2乗を展開しながら式を整理します。
\frac{1}{N} \sum_{i=1}^{N} (X_i^t v)^2
= \frac{1}{N} \sum_{i=1}^{N} (X_i^t v)^t(X_i^t v) \\
= \frac{1}{N} \sum_{i=1}^{N} (v^t X_i)(X_i^t v) \\
= \frac{1}{N} \sum_{i=1}^{N} v^t X_i X_i^t v \\
= v^t (\frac{1}{N}\sum_{i=1}^{N}X_i X_i^t) v \\
= v^t \Sigma v
ただし、
\Sigma = \frac{1}{N}\sum_{i=1}^{N}X_i X_i^t
である。
ここで、
\Sigma = \frac{1}{N}\sum_{i=1}^{N}X_i X_i^t
=\begin{pmatrix}
\frac{1}{N}\sum_{i=1}^{N}x_i^2 & \frac{1}{N}\sum_{i=1}^{N}x_iy_i\\
\frac{1}{N}\sum_{i=1}^{N}y_ix_i & \frac{1}{N}\sum_{i=1}^{N}y_i^2
\end{pmatrix}
となります。さらに今回中央化をしているため、標本平均は0です。したがって、上記の式は下記のようになります。
\Sigma
=\begin{pmatrix}
\frac{1}{N}\sum_{i=1}^{N}x_i^2 & \frac{1}{N}\sum_{i=1}^{N}x_iy_i\\
\frac{1}{N}\sum_{i=1}^{N}y_ix_i & \frac{1}{N}\sum_{i=1}^{N}y_i^2
\end{pmatrix}
= \begin{pmatrix}
\text{Var}(X') & \text{Cov}(X', Y')\\
\text{Cov}(X', Y') & \text{Var}(Y')
\end{pmatrix}
したがって、これはX'とY'の二つの次元における分散共分散行列の定義式と一致するため、\Sigmaは分散共分散行列です。
ラグランジュの未定乗数法
ここまでで、解きたいのは、
\lvert v \rvert ^2 = 1の条件下での、v^t \Sigma vを最大にするvになります。
このような制約付き最適化問題を解く際は、ラグランジュの未定乗数法が利用できます。
まず、ラグランジュ乗数を\lambdaとして、目的関数f(v) = v^t \Sigma vと制約g(v) = v^t v - 1 = 0を利用して、ラグランジュ関数\mathcal{L}(v, \lambda)を次のように定義します。
\mathcal{L}(v, \lambda) = v^t \Sigma v - \lambda (v^t v - 1)
ここでラグランジュの未定乗数法により、下記を解くことで分散を最大にする基底ベクトルvを得ることができます。
\frac{\partial \mathcal{L}}{\partial v} = 0
\frac{\partial \mathcal{L}}{\partial \lambda} = 0
上記の条件により下記が成立します。
\frac{\partial \mathcal{L}}{\partial v} = 2 \Sigma v - 2\lambda v = 0
また、
\frac{\partial \mathcal{L}}{\partial \lambda} = -(v^t v - 1) = 0
です。
ここで、二つ目の条件は、制約条件と同一のため無視して大丈夫ですが、一つ目の条件\Sigma v = \lambda vに着目すると、これは分散共分散行列の固有値問題になっていることがわかります。
したがって、前回の記事で解説した通り、分散共分散行列の固有値分解を解くことこそが、主成分分析による分散を最大化する基底ベクトルvを見つけることであるということが説明できました。
λの意味
では、この固有値問題を解いて得られる\lambdaとは何者なのでしょうか。
結論から言うと、求めたい分散の値そのものになります。
では、説明していきます。
まず、ラグランジュの未定乗数法の一つ目の条件により、下記が成立しています。
ここに、両辺の最初の項にv^tの変換を適用させることを考えます。
\Sigma v = \lambda v \\
v^t \Sigma v = v^t \lambda v \\
v^t \Sigma v = \lambda v^t v \\
v^t \Sigma v = \lambda
と変形させることができます。最後の行の式変形は、制約条件\lvert v \rvert ^2 = 1を利用しています。
このとき、式の左辺は、今回最大化したい分散の値になっていることがわかります。
したがって、ラグランジュの未定乗数法で得られるラグランジュ定数\lambdaは分散そのものを表していることが説明できました。
2軸目の選定
2軸目が満たすべき条件
さて、実は先ほど得られた固有値問題を解くと複数の\lambdaの値が解になり、それら全てに対して固有ベクトルvが存在することがわかっています。
実際、今回のような2次元のデータで考えた場合、\lambdaは最大2つの解を持ちます。N次元のデータの場合は最大N個の解を持ちます。
先ほどの節において\lambdaは分散そのものであると言う話をしました。したがって主成分分析における分散を最大にする軸(基底ベクトル)を決定するためには、\lambdaが最も大きい時に対応する基底ベクトルvを選ぶことによって達成されます。
データが2次元の場合はそれで次元削減が完了しますが、3次元や4次元の場合はどうでしょうか・・・
2軸目をどのように選ぶべきかわからないですよね。
結論を言うと、2軸目は固有値問題を解いた際の、2番目に大きい\lambdaに対応する固有ベクトルを基底ベクトルとした軸を選ぶことで、次に分散を最大化できる軸を引くことができます。
3番目も4番目も同様に、N次元のデータであれば、最大N個の\lambdaと固有ベクトルの組が得られるため、\lambdaが大きい順に固有ベクトルは分散を最大にする軸になります。
では、上記についても説明しましょう。
まず、1軸目を与える\lambdaと固有ベクトルの組みが(\lambda_1, v_1)で得られているものとします。
このとき2軸目の条件としては、1軸目と「直交」していて、かつ分散を最大にする軸である必要があります。
この直交というのが重要です。例えばxyz空間のグラフを想像していただくとわかりますが、それぞれ3つの軸は全て90度で交わっていると思います。これが直交という概念です。
今回も、新たな軸を作る際に、これまでの全ての軸と直交することを追加の条件として加えます。
ここで2軸目に相当する基底ベクトルv_2を考えると、直交の条件は下記になります。
また1軸目と同様に下記の条件も存在します。
ラグランジュの未定乗数法を再度利用
では、この2つの条件下での分散最大化問題を解くために、改めてラグランジュの未定乗数法を利用します。
\mathcal{L}(v_2, \lambda_2, \mu) = v_2^t \Sigma v_2 - \lambda_2 (v_2^t v_2 - 1) - \mu v_1^t v_2
ここで、\lambda_2と\muがラグランジュ定数です。
そして、分散v_2^t \Sigma v_2を制約下で最大にするには、下記を満たすvを求めます。
\frac{\partial \mathcal{L}}{\partial v_2} = 0
\frac{\partial \mathcal{L}}{\partial \lambda_2} = 0
\frac{\partial \mathcal{L}}{\partial \mu} = 0
上記より、下記が成立します。
\frac{\partial \mathcal{L}}{\partial v_2} = 2 \Sigma v_2 - 2 \lambda_2 v_2 - \mu v_1 = 0
したがって、
\Sigma v_2 = \lambda_2 v_2 + \frac{\mu}{2} v_1
また、
\frac{\partial \mathcal{L}}{\partial \lambda_2} = -(v_2^t v_2 - 1) = 0
\frac{\partial \mathcal{L}}{\partial \mu} = -v_1^t v_2 = 0
です。
下2つは制約条件をあらためて記述しているだけなので、無視して良いです。問題は一番上の式です。
\Sigma v_2 = \lambda_2 v_2 + \frac{\mu}{2} v_1
固有値問題に帰着させる
\Sigma v_2 = \lambda_2 v_2 + \frac{\mu}{2} v_1
この式の問題は、純粋な固有値問題になっていないため、解けないことです。しかしながら、ここに制約条件v_1^t v_2 = 0が効いてきます。
まず、両辺にv_1^tを掛けます
v_1^t \Sigma v_2 = v_1^t(\lambda_2 v_2 + \frac{\mu}{2} v_1)
ここで一旦左辺から分析します。
左辺v_1^t \Sigma v_2は、下記のように変形できます。
v_1^t \Sigma v_2 = (\Sigma^t v_1)^t v_2 = (\Sigma v_1)^t v_2 = (\lambda_1 v_1)^t v_2 = \lambda_i v_1^t v_2 = 0
ここでは、分散共分散行列\Sigmaが対称行列であるため\Sigma^t = \Sigmaであることと、制約(直交)条件v_1^t v_2 = 0を利用しています。
したがって、左辺は0であることがわかりました。
続いて右辺を展開すると、
v_1^t(\lambda_2 v_2 + \frac{\mu}{2} v_1) = \lambda_2 v_1^t v_2 + \frac{\mu}{2} v_1^t v_1
となり、ここでも制約条件により、
\lambda_2 v_1^t v_2 + \frac{\mu}{2} v_1^t v_1 = \frac{\mu}{2}
となります。
したがって、左辺が0であったことから
となることがわかりました。
ここで、今求めたことにより、ラグランジュの未定乗数法で得られた最初の条件式は、
\Sigma v_2 = \lambda_2 v_2 + \frac{\mu}{2} v_1
\Sigma v_2 = \lambda_2 v_2
とできるため、完全に1軸目と同様の式に変わりました。
1軸目と異なる\lambdaを選定する必要があるため、2番目に大きい\lambdaを選定することで2軸目を決定することができます。
k軸目を考える
では、2次元の論証を参考にして、k軸目に拡張します。
k軸目(の固有ベクトル)が満たす条件
問題設定を整理します。
まず、標本全体Sは下記とします。
S=\{X_1,X_2,......,X_{N}\}
Nはサンプルサイズです。
このとき、各サンプルはn次元のデータを考え、k \in \mathbb{N}, \quad 1 \leq k \leq nを満たすk軸目をどのように得るかを考えます。
すなわち、あるインデックスiにおけるサンプルは、下記のように表記できます。
X_i = \begin{pmatrix}
x_{i1} \\
x_{i2} \\
\vdots \\
x_{in}
\end{pmatrix} \quad \text{for} \quad i = 1, 2, \dots, N
このとき、k軸目に対応する固有ベクトルv_kは、k-1番目までのすべての固有ベクトルと直交しており、さらに\lvert v_k \rvert ^2 = 1である必要があります。
これを制約条件として下記のように記載します。
g_0(v) = v_k^t v_k - 1 = 0
g_i(v) = v_i^t v_k = 0 \quad \text{for} \quad i = 1, 2, \dots, k-1
ラグランジュの未定乗数法を利用する
では、このk個の制約条件下での分散v_k^t \Sigma v_kの最大化問題を解くために、ラグランジュの未定乗数法を再度利用します。
\mathcal{L}(v_2, \lambda_k, \mathbf{\mu}) = v_k^t \Sigma v_k - \lambda_k (v_k^t v_k - 1) - \sum_{i=1}^{k-1}{\mu_i v_i^t v_k}
ただし、
\mathbf{\mu} = \{\mu_1, \mu_2, \dots, \mu_{k-1}\}
このとき、分散v_k^t \Sigma v_kを制約条件下で最大化するv_kは下記を満たします。
\frac{\partial \mathcal{L}}{\partial v_k} = 0
\frac{\partial \mathcal{L}}{\partial \lambda_k} = 0
\frac{\partial \mathcal{L}}{\partial \mu_i} = 0 \quad \text{for} \quad i = 1, 2, \dots, k-1
これまでの議論と同様に、下二つの条件は制約条件(g_0(v)、g_i(v))を改めて書き下しているだけのため、無視することができ、一番上の条件だけが残ります。
\frac{\partial \mathcal{L}}{\partial v_k} = 2 \Sigma v_k - 2 \lambda_k v_k - \sum_{i=1}^{k-1}{\mu_i v_i} = 0
\Sigma v_k - \lambda_k v_k - \frac{1}{2}\sum_{i=1}^{k-1}{\mu_i v_i} = 0
したがって、
\Sigma v_k = \lambda_k v_k + \frac{1}{2}\sum_{i=1}^{k-1}{\mu_i v_i}
固有値問題に帰着させる
さて、2軸目の議論と同様に、邪魔な\mu_iを消して、固有値問題に帰着させます。
まず、両辺にv_l^tをかけます。
ただし、l = 1, 2, \dots, k-1となる自然数です。
v_l^t \Sigma v_k = v_l^t (\lambda_k v_k + \frac{1}{2}\sum_{i=1}^{k-1}{\mu_i v_i})
左辺に着目すると下記の変形が成立します。
v_l^t \Sigma v_k = (\Sigma^t v_l)^t v_k = (\Sigma v_l)^t v_k = (\lambda_l v_l)^t v_k = \lambda_l v_l^t v_k = 0
分散共分散行列\Sigmaが対称行列であることと、制約条件(g_i(v))から、
上記の変形は、l = 1, 2, \dots, k-1のすべてのlについて成立します。
続いて右辺を変形します。
v_l^t (\lambda_k v_k + \frac{1}{2}\sum_{i=1}^{k-1}{\mu_i v_i}) \\
= v_l^t \lambda_k v_k + \frac{1}{2} v_l^t \sum_{i=1}^{k-1}{\mu_i v_i} \\
= \lambda_k v_l^t v_k + \frac{1}{2} \sum_{i=1}^{k-1}{\mu_i v_l^t v_i}
ここで右辺の第1項は、制約条件(g_i(v))から0になります。
(v_l^t v_k = 0)
右辺の第2項に関しては、\sum_{i=1}^{k-1}の中身のiがlと等しいときと異なるときで利用する制約条件が変わります。
iがlと等しいときは、制約条件(v_l^t v_l = 1)が適用され、iがlと異なるときは、制約条件(v_l^t v_i = 0)が適用されるため、クロネッカーのデルタ\delta_{il}を導入すると、下記のように書けます。
\lambda_k v_l^t v_k + \frac{1}{2} \sum_{i=1}^{k-1}{\mu_i v_l^t v_i} \\
= 0 + \frac{1}{2} \sum_{i=1}^{k-1}{\mu_i \delta_{il}} \\
= \frac{1}{2} \mu_l
したがって、左辺が0であるため、
となります。
これはとりうる全てのl = 1, 2, \dots, k-1について成立するため、
\Sigma v_k = \lambda_k v_k + \frac{1}{2}\sum_{i=1}^{k-1}{\mu_i v_i}
\Sigma v_k = \lambda_k v_k
と変形でき、単純な固有値問題に帰着させることができました。
これは最初に解いた固有値問題と同一であることがわかります。
したがって、k軸目に対応する固有ベクトルv_kを選ぶ際には、固有ベクトルv_kはそれまでのk-1個の固有ベクトルと直行している必要があるため、固有値問題を解いた場合の、上からk番目の固有値\lambda_kに対応するv_kを基底ベクトルとして選びます。
結論
以上により、各軸において、それまでのすべての軸と直交しながら、その中で分散を最大にする軸を選ぶには、固有値問題を解いた際の固有値\lambdaが大きい順に対応する基底ベクトルを軸に選ぶことで、失う情報を最小限にしながら次元を削減する軸を決定することができます。
まとめ
ここまでで、主成分分析に関して、「何を目的に次元削減しているのか」という点からスタートして、実際に何をやっているのかを数式で説明しました。
その中で、前回の記事ではスルーしていた、分散共分散行列と主成分分析の数式での関係を説明できたかなと思います。
特に、k軸目まで一般化して説明している記事はあまりないと思いますので、参考になれば幸いです。
ここまで読んでくださってありがとうございました!
参考文献
主成分分析(PCA)の気持ち
妥協しないデータ分析のための 微積分+線形代数入門





Discussion