分散共分散行列の魅力

はじめに

生成AIを勉強する中で、正規（ガウス）分布は非常によく出てくる分布です。その分布を決定づけるのは平均と分散共分散行列になります。

今回は、この分散共分散行列って、実はかなり有用で本質的な値（もしかしたら平均値や中央値よりも）なのではないか？と思ったため、その思いを殴り書きしていこうと思います。

分散共分散行列を知ることで、PCAを利用した次元削減の意味が分かるようになります。
さらに、分散共分散行列を利用して、下記のように、固有ベクトルの向きに従って分布を変換することができるようになります。

皆さんにも、分散共分散行列の魅力をわかりやすく伝えられれば幸いです。

（追記）
続編書きました！
https://zenn.dev/asap/articles/ff8f34d19ca6a4

平均値では表現できない性質

得られたデータ点を分析する際に、平均値や中央値は直感的に理解しやすく（また、他人に理解してもらいやすく）よく使われる指標だと思います。

例えば、こちらのサイトでは、2019年の年齢別の身長と体重の平均値を見ることができ、17歳男性の場合、平均身長はそれぞれ、171.5cm、64.0kgであると記載されており、17歳の男性は平均的にその程度の身長であることがわかります。

ただし、平均値は、一部の身長が高い人や身長が低い人などに引っ張られて、直感と異なる値が出ることがあります。これは分布が正規分布として見做せない場合（例えば社会人の平均年収）などで発生しやすく、その場合は、中央値を利用することで、社会人の大体真ん中くらいの年収がいくらなのかを知ることができます。

例えば、こちらのサイトによると、2022年の日本全体の平均世帯年収は545.7万円ですが、中央値で見ると、423万円となっており、このデータが正しいかどうかわからないですが、平均値を中央値で大きな乖離があることがわかります。

平均値　中央値

平均値はデータ全体の合計をデータの個数で割った値です。
例えば、テストの点数が5人の生徒で10点、70点、80点、90点、100点だとしたら、それらの点数をすべて足して人数で割ることで平均点を求めることができます。この場合の平均点は70点になります。平均値は全体の傾向を知るのに便利ですが、極端に大きな値や小さな値があると、その影響を受けやすいのが特徴です。
例えば、テストの点数の例では、一人が10点という非常に低い点数をとっているため、平均点は70点になってしまっています。
これでは、6人目の生徒がたとえ70点を取ったとしても、順位は真ん中より下になってしまいます。

一方、中央値はデータを小さい順に並べたとき、ちょうど真ん中にくる値です。
データの数が奇数ならそのまま真ん中の値が中央値になり、偶数なら真ん中の2つの値の平均を取ります。先ほどのテストの点数で考えると、10点、70点、80点、90点、100点を小さい順に並べると、真ん中にくるのは80点なので、これが中央値です。中央値の強みは、極端な値に左右されにくい点です。
テストの点数の例では、一人が10点という非常に低い点数をとっていますが、この点数には左右されない真ん中の順位の値を知ることができます。

つまり、平均値はデータ全体の傾向を示すものの、外れ値の影響を受けやすく、中央値はデータの中央に位置する値を示すため、外れ値の影響を受けにくいという違いがあります。それぞれの特徴を理解して使い分けることが、データ分析では重要です。

さて、平均値や中央値を利用することで、データ点全体の「真ん中」を知ることができます。
データの真ん中を知ることができれば、分布間の比較や効果の高い施策の検討を行うことができます。
例えば、チーム間の平均売上を比較することで、チームの成果を比較することができたり、また、マーケティングなどの分野では、（正規分布では）、平均値付近のターゲットは多いことが期待できるため、その層に向けた施策を打つことで、効率的なマーケティングに活かすことができます。

しかしながら、これらの値は、データ点がどのように分布しているかを知ることはできません。

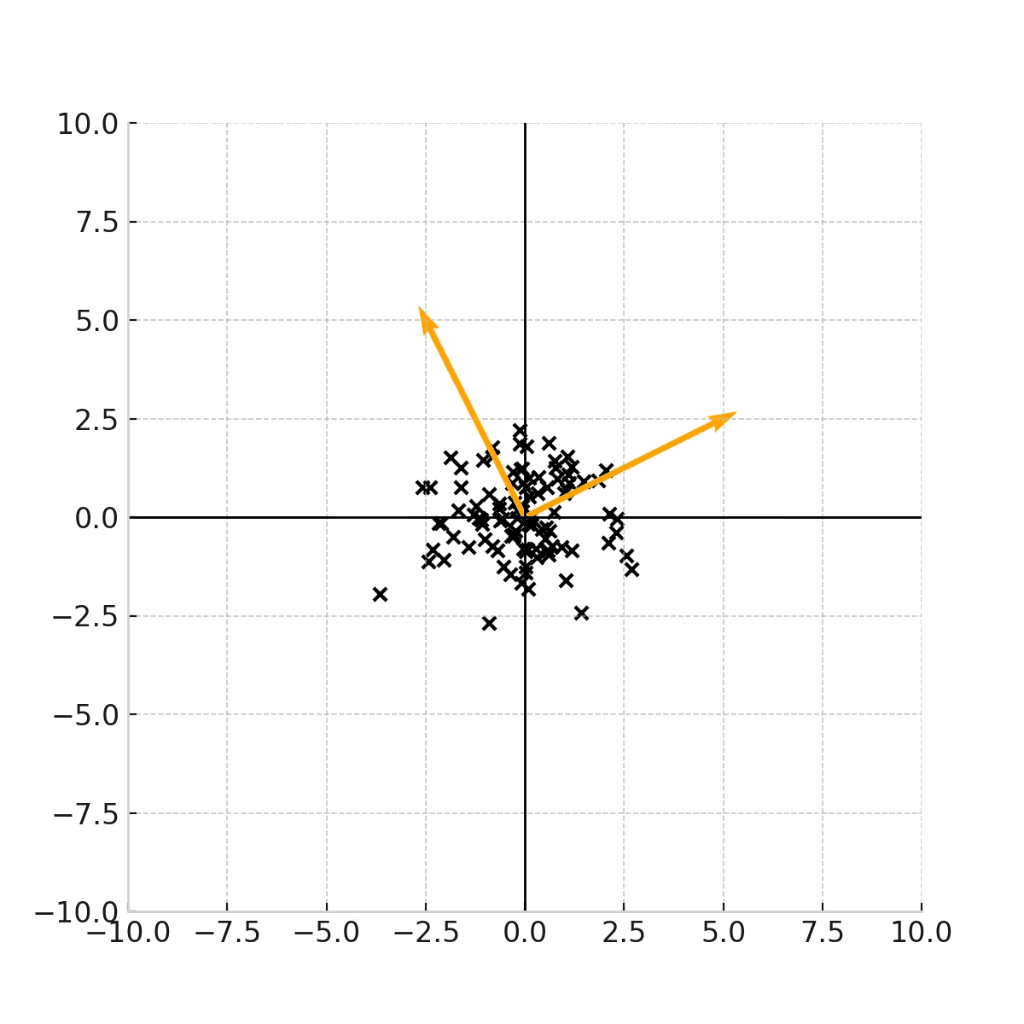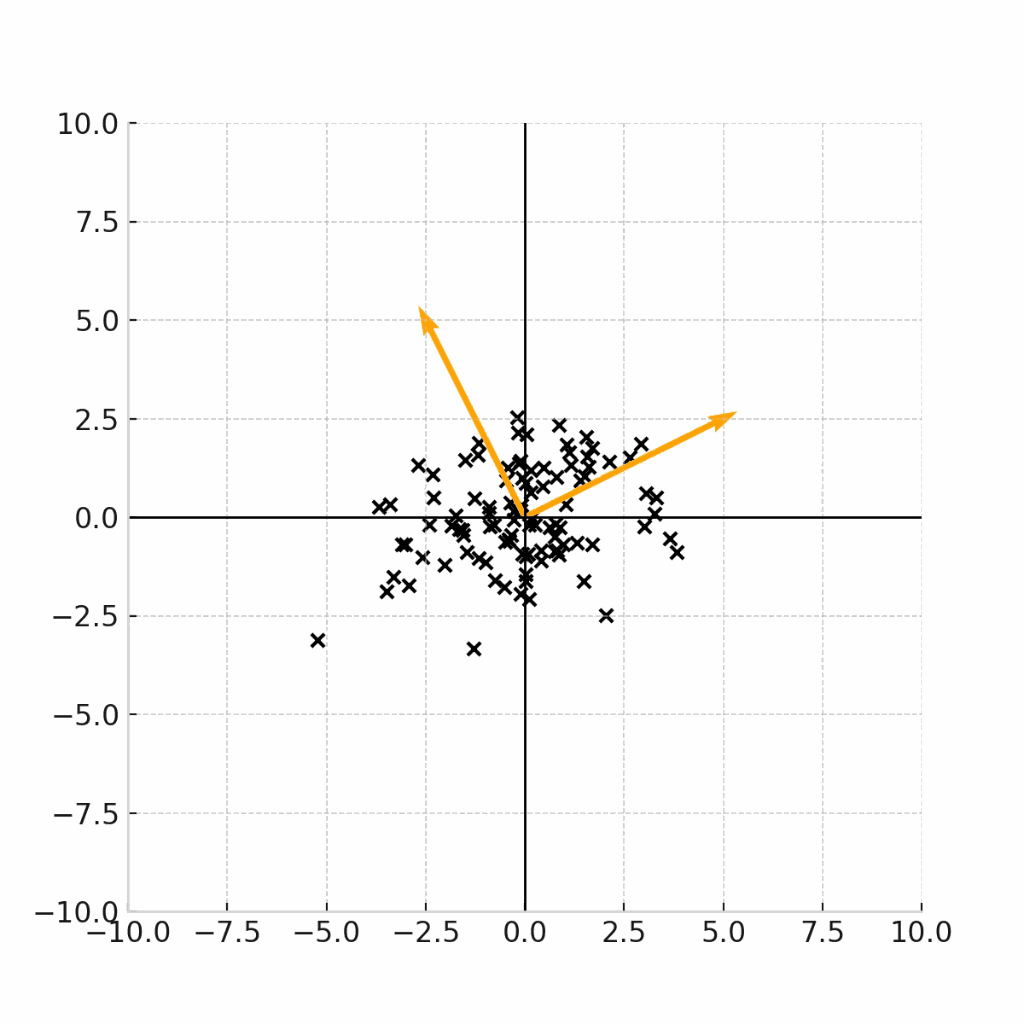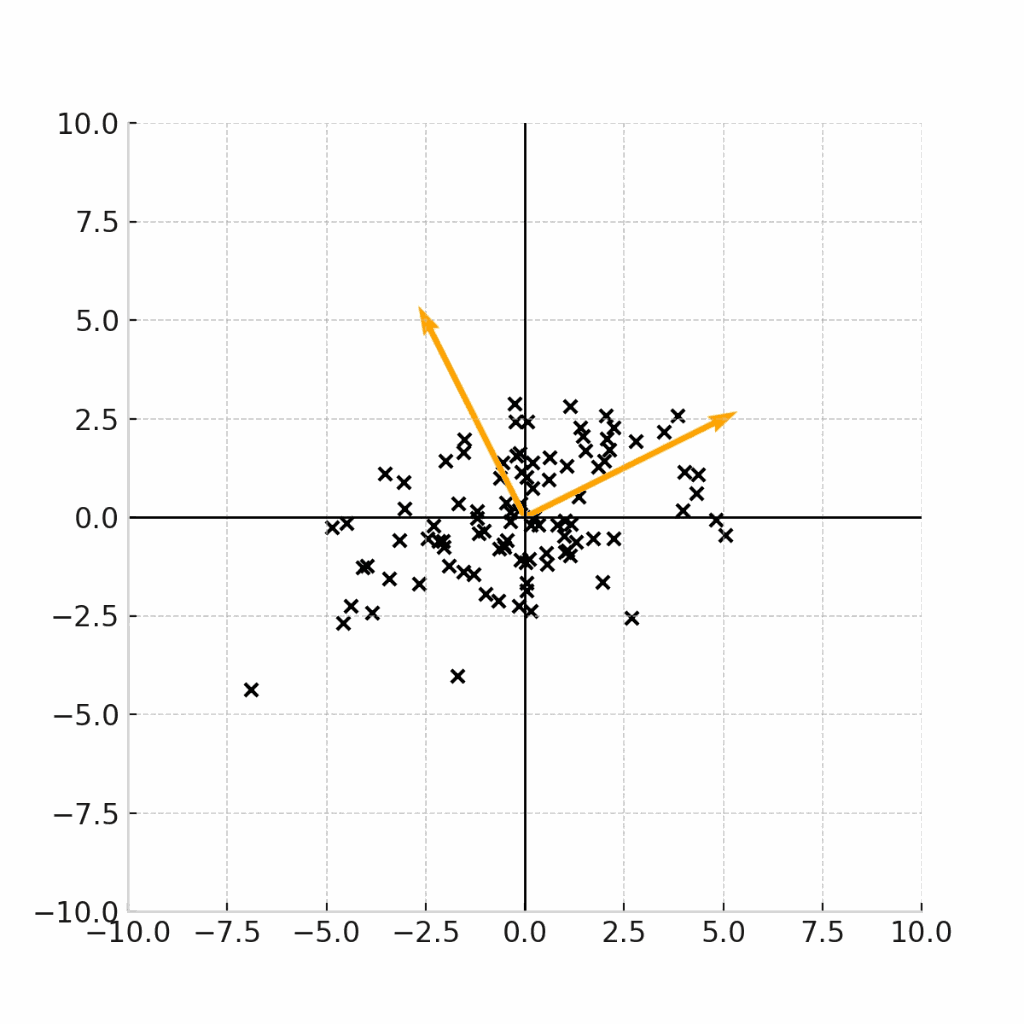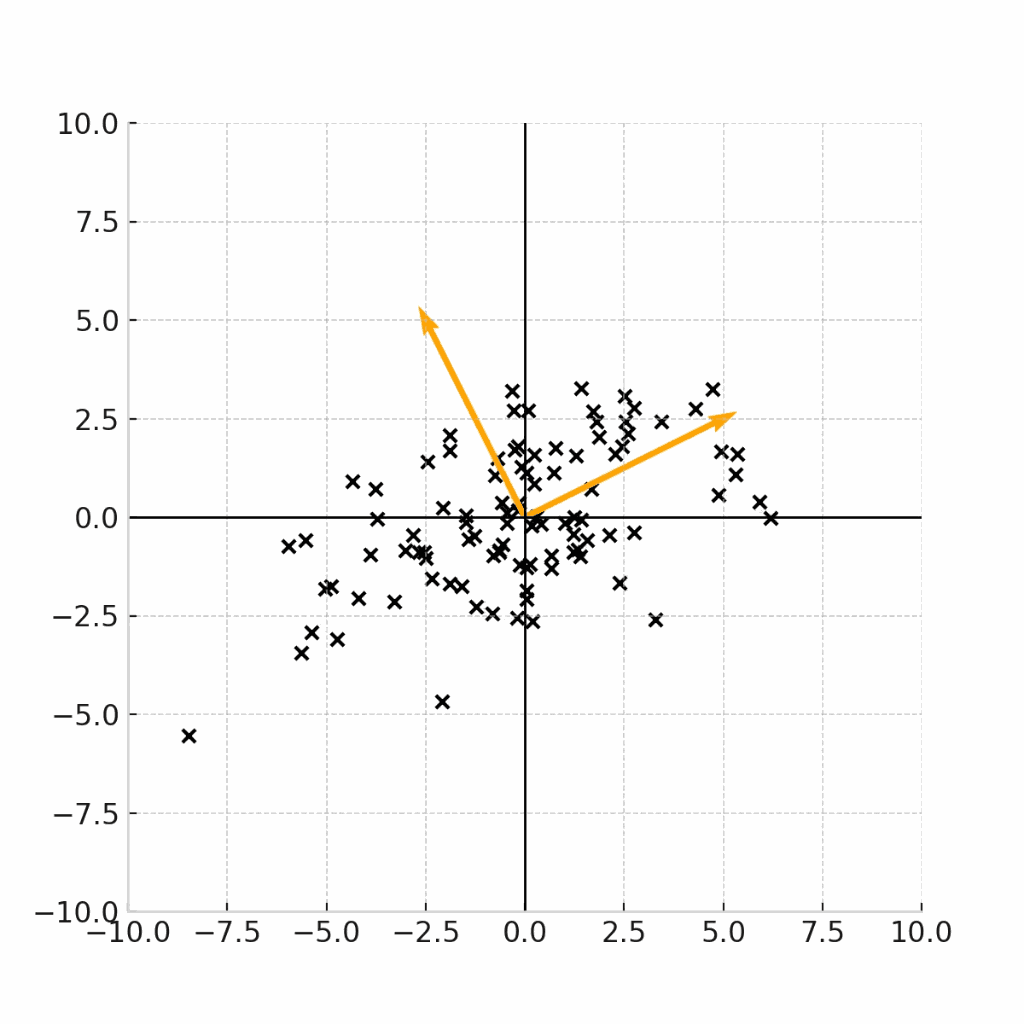
例えば下記の4つのデータ点の例は、全て、平均が$(0,0)$であるデータ点の例です。

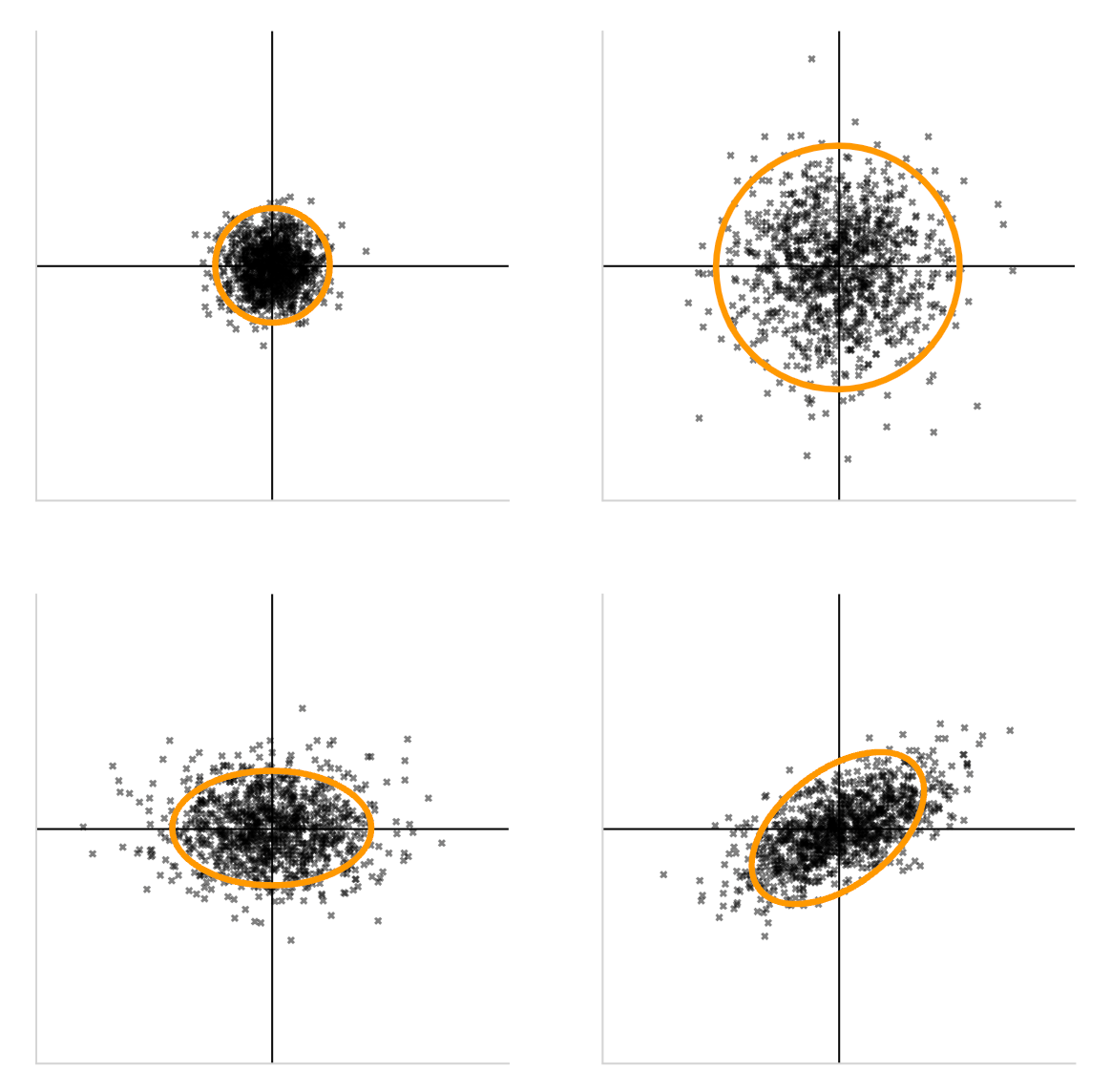
例えば、この原点を$($身長$,$体重$) = (171.5,64.0)$の点であると考えると、これらのグラフは、17歳男性の身長と平均のデータ点をプロットした図であると考えることができます。

では、（現実的に）正しいデータをプロットした図はどれになるでしょうか。
ここで重要なのは、身長と体重という二つの変数に相関があるのかどうかです。

一般的には身長が高い人の方が体重が高いという正の相関が見られることが期待されるため、現実的に正しいデータがプロットされたグラフは、右下のグラフであることがわかります。

で、あるにもかかわらず、右上のような「身長と体重が独立になっている」グラフを前提として、平均値や中央値だけで議論しても、意義のある考察結果は得られません。
最悪の場合、全く的外れな考察結果を、数字を使って説明してしまうことになります。

このように、データを分析する際には、平均値や中央値だけでなく、分布全体の形を決めるような新たな評価指標が非常に重要になってきます。

その評価指標の一つとして、分散共分散行列が存在します。

分散共分散行列

定義

分散共分散行列$\Sigma$は下記で定義されます。

$$\Sigma = \begin{pmatrix} \text{Var}(X_1) & \text{Cov}(X_1, X_2) & \cdots & \text{Cov}(X_1, X_n) \\ \text{Cov}(X_2, X_1) & \text{Var}(X_2) & \cdots & \text{Cov}(X_2, X_n) \\ \vdots & \vdots & \ddots & \vdots \\ \text{Cov}(X_n, X_1) & \text{Cov}(X_n, X_2) & \cdots & \text{Var}(X_n) \end{pmatrix}$$

ここで、$X_1,X_2,X_3 \cdots X_n$は、$n$種類の変数を表しています。
例えば、「身長」と「体重」で考えると、$n=2$となります。

加えて、母集団に基づいた場合、
分散$\text{Var}(X_i)$は

$$\text{Var}(X_i) = \mathbb{E}[(X_i - \mathbb{E}[X_i])^2$$

また、共分散$\text{Cov}(X_i, X_j)$は

$$\text{Cov}(X_i, X_j) = \mathbb{E}[(X_i - \mathbb{E}[X_i])(X_j - \mathbb{E}[X_j])]$$

で定義されます。

身長と体重の例で考える

変数が$n$種類あると、理解しにくいため、具体的に考えてみましょう。
今回は$n=2$の身長と体重で考えてみます。

ここで、身長を$X$、体重を$Y$で表すと、分散共分散行列$\Sigma$は、

$$\Sigma = \begin{pmatrix} \text{Var}(X) & \text{Cov}(X, Y)\\ \text{Cov}(X, Y) & \text{Var}(Y) \end{pmatrix}$$

となります。

標本データから分散、共分散を計算する

$X=(x_1,x_2,x_3, \cdots ,x_N)$と$Y=(y_1,y_2,y_3, \cdots ,y_N)$という$N$個の標本データが与えられているとします。

共分散行列の分散と共分散は、標本に基づいて定義すると、下記のようになります。

$$\text{Var}(X) = \frac{1}{N} \sum_{i=1}^{N} (X_i - \bar{X})^2$$

$$\text{Cov}(X, Y) = \frac{1}{N} \sum_{i=1}^{N} (X_i - \bar{X})(Y_i - \bar{Y})$$

ただし、$\bar{X}$は$X$の標本平均を表し、下記でかけます。

$$\bar{X} = \frac{1}{N} \sum_{i=1}^{N} X_i$$

分散の意味

分散は母集団における期待値$\mathbb{E}[X_i]$で定義すると下記のようになり、

$$\text{Var}(X_i) = \mathbb{E}[(X_i - \mathbb{E}[X_i])^2$$

標本における標本平均$\bar{X}$を用いて定義すると下記のようになります。

$$\text{Var}(X) = \frac{1}{N} \sum_{i=1}^{N} (X_i - \bar{X})^2$$

どちらの式も同様の意味ですが、わかりやすく標本平均を用いた、下の式で説明します。

ここでは$X$は17歳の男性の身長のデータと仮定します。
例えば、100人分のデータを持っていれば$N=100$となるため、分散は下記の式になります。

$$\text{Var}(X) = \frac{1}{100} \sum_{i=1}^{100} (X_i - \bar{X})^2$$

ここで、$(X_i - \bar{X})^2$は、平均値からの標本の2乗誤差を計算しています。
2乗しているのは、誤差は正の誤差と負の誤差があるため、単純に足し合わせると誤差が打ち消しあってしまうため。2乗することで、正の誤差も負の誤差も正の値にしています。

分散では、その値を標本の数だけ足し合わせているため、標本データが平均値から離れているデータが多い場合は、分散が大きくなります。

したがって、分散はデータのばらつき度合いを表していると言えます。

共分散の意味

共分散は母集団における期待値$\mathbb{E}[X_i]$で定義すると下記のようになり、

$$\text{Cov}(X_i, X_j) = \mathbb{E}[(X_i - \mathbb{E}[X_i])(X_j - \mathbb{E}[X_j])]$$

標本における標本平均$\bar{X}$を用いて定義すると下記のようになります。

$$\text{Cov}(X, Y) = \frac{1}{N} \sum_{i=1}^{N} (X_i - \bar{X})(Y_i - \bar{Y})$$

分散と似た式ですが、分散と異なるのは、$X$と$Y$の二つに対して、平均からの標本誤差を評価して、掛け合わせているということです。

この式からわかるのは、もし$x_i$と$y_i$がどちらも平均に対して正の誤差、もしくは負の誤差を持つ場合は、$(X_i - \bar{X})(Y_i - \bar{Y})$の値は正になりますが、$x_i$が正の誤差を持つ時に、$y_i$が負の誤差を持つ場合や、$x_i$が負の誤差を持つ時に、$y_i$が正の誤差を持つ場合は、$(X_i - \bar{X})(Y_i - \bar{Y})$の値は負の値になります。

すなわち、$x_i$と$y_i$の平均に対しての標本誤差の正負が一致している場合は、正になり、一致していない場合は負の値になります。

具体的に考えると、ある特定の17歳の男性の身長と体重で考えたときに、身長と体重がどちらも平均値より高い、もしくは低い場合は、正の値になりますが、身長は平均以上だが、体重が平均以下などの場合は、負の値になるということです。

すなわち、共分散は、2つの変数の相関を表しています。

分散共分散行列と正規分布

改めて分散共分散行列は下記でかけます。

$$\Sigma = \begin{pmatrix} \text{Var}(X_1) & \text{Cov}(X_1, X_2) & \cdots & \text{Cov}(X_1, X_n) \\ \text{Cov}(X_2, X_1) & \text{Var}(X_2) & \cdots & \text{Cov}(X_2, X_n) \\ \vdots & \vdots & \ddots & \vdots \\ \text{Cov}(X_n, X_1) & \text{Cov}(X_n, X_2) & \cdots & \text{Var}(X_n) \end{pmatrix}$$

分散共分散行列は、その対角成分に分散を、それ以外の要素に、該当する共分散をもつ行列です。

つまり分散共分散行列は各変数の分布のばらつき度合いと、各変数間の相関関係を記述した行列です。したがってこの行列があれば分布の形を推測することができます。

正規分布

ここで正規分布を考えます。
正規分布は統計学において最も基本的でよく使われる確率密度関数の一つです。
データが正規分布に従う場合、そのデータから「平均値を中心に対称な形」で分布し、中央付近にデータが集中していて、平均から離れるほどデータが少なくなる特徴があります。

1変数正規分布

1変数正規分布とは、下記のような式で表される分布をいいます。

$$N(x; \mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)$$

ここで$\mu$はデータの平均、$\sigma^2$はデータの分散です。

上記の分布は図にすると下記のようなベルカーブを描く分布になり、山が一番高くなる横軸上の点の数値が平均$\mu$になります。

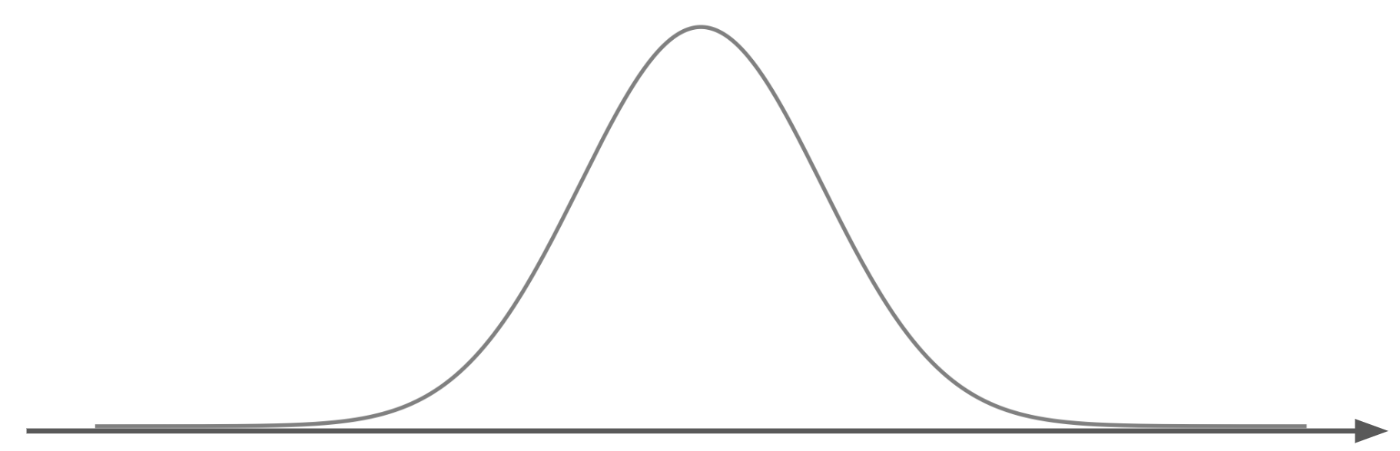
こちらの図のように、平均付近が最もデータ数が多く、離れるにつれてデータ数が少なくなっていることがわかります。

この分布の形を調整するパラメータは、平均$\mu$と分散$\sigma^2$です。この二つの値によって、分布の形が変わります。

平均を大きくすると、正規分布は形を保ったまま右に並行移動し、分散を大きくすると、分布の中心の位置を保ったまま、左右に分布が引き伸ばされるように変換されます。

他変数正規分布

1変数の場合は、変数が1つなため、分布を決定づけるパラメータは平均$\mu$と分散$\sigma^2$の二つだけですが、他変数に拡張する場合はどうしたらいいでしょうか？

2変数の正規分布を考えてみましょう。
一番簡単なのは、1変数の正規分布を二つ用意して、$x$軸と$y$軸の両方に正規分布を適応することです。

つまり下記のような式です。

$$N(z; \mu_z, \sigma_z^2) = \frac{1}{\sqrt{2\pi\sigma_x^2}} \exp\left(-\frac{(x - \mu_x)^2}{2\sigma_x^2}\right) \times \frac{1}{\sqrt{2\pi\sigma_y^2}} \exp\left(-\frac{(y - \mu_y)^2}{2\sigma_y^2}\right)$$

$$= \frac{1}{2\pi\sigma_x\sigma_y} \exp\left(-\left(\frac{(x - \mu_x)^2}{2\sigma_x^2} + \frac{(y - \mu_y)^2}{2\sigma_y^2}\right)\right)$$

ただし

$$\mathbf{z} = \begin{pmatrix} x \\ y \end{pmatrix}$$

$$\mathbf{\mu_z} = \begin{pmatrix} \mu_x \\ \mu_y \end{pmatrix}$$

$$\mathbf{\sigma_z} = \begin{pmatrix} \sigma_x \\ \sigma_y \end{pmatrix}$$

上記の式でも同様に、平均を動かすと、並行移動し、分散を大きくすると、その軸方向にデータのばらつきが増えます。

しかしながら、これだけでは、データ間に相関があるような正規分布を用意することができません。
それは下記の式を式変更することで簡単に説明できます。

$$N(z; \mu_z, \sigma_z^2) = \frac{1}{2\pi\sigma_x\sigma_y} \exp\left(-\left(\frac{(x - \mu_x)^2}{2\sigma_x^2} + \frac{(y - \mu_y)^2}{2\sigma_y^2}\right)\right)$$

ここで、

$$\Sigma = \begin{pmatrix} \sigma_x^2 & \text{Cov}(X, Y)\\ \text{Cov}(X, Y) & \sigma_y^2 \end{pmatrix}$$

とすると、

$$\Sigma I = \begin{pmatrix} \sigma_x^2 & 0\\ 0 & \sigma_y^2 \end{pmatrix}$$

となるため、下記のようになります。

対角行列の行列式のため下記のように計算できます。

$$\det(\Sigma I) = \sigma_x^2\sigma_y^2$$

また、対角行列の逆行列は非常に簡単に計算できます。具体的には下記の通りです。

$$\begin{pmatrix} \sigma_x^2 & 0\\ 0 & \sigma_y^2 \end{pmatrix}^{-1}= \begin{pmatrix} \frac{1}{\sigma_x^2} & 0\\ 0 & \frac{1}{\sigma_y^2} \end{pmatrix}$$

したがって、下記の式変換が成立します。

$$(\mathbf{z} - \mathbf{\mu_z})^\top (\Sigma I)^{-1} (\mathbf{z} - \mathbf{\mu_z})= \begin{pmatrix} x - \mu_x \\ y - \mu_y \end{pmatrix}^\top \begin{pmatrix} \frac{1}{\sigma_x^2} & 0\\ 0 & \frac{1}{\sigma_y^2} \end{pmatrix} \begin{pmatrix} x - \mu_x \\ y - \mu_y \end{pmatrix}= \left(\frac{(x - \mu_x)^2}{\sigma_x^2} + \frac{(y - \mu_y)^2}{\sigma_y^2}\right)$$

したがって、

$$N(z; \mu_z, \sigma_z^2) = \frac{1}{2\pi\sigma_x\sigma_y} \exp\left(-\left(\frac{(x - \mu_x)^2}{2\sigma_x^2} + \frac{(y - \mu_y)^2}{2\sigma_y^2}\right)\right)$$

$$=\frac{1}{2 \pi |\Sigma I|^{1/2}} \exp \left( -\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu})^T (\Sigma I)^{-1} (\boldsymbol{x} - \boldsymbol{\mu}) \right)$$

と表記変えできます。
上記の式の分散部分を見るとわかるように、分散共分散行列$\Sigma$ではなく$\Sigma I$が使われています。

この$\Sigma I$は非対角成分は0であるため、$X$と$Y$の共分散が0になっています。共分散の式からわかるように、。共分散が0というのは、二つの変数間に相関が全くない（つまり独立である）ことを示します。

では、どうやって変数間の相関を考慮した、他変数の正規分布を用意するかというと、単純に$\Sigma I$ではなく$\Sigma$を利用するだけです。

そもそもの問題は$\Sigma I$の非対角成分（つまり共分散）が単位行列$I$によって0にされていることが問題なため、元々の$\Sigma$を利用することで、相関も考慮した正規分布を表現できます。

実際に、他変数の正規分布は下記の式で表されています。

$$N(z; \mu, \Sigma) = \frac{1}{2 \pi |\Sigma|^{1/2}} \exp \left( -\frac{1}{2} (\boldsymbol{x} - \boldsymbol{\mu})^T \Sigma^{-1} (\boldsymbol{x} - \boldsymbol{\mu}) \right)$$

上記の式展開は、正式な導出ではなく、あくまで1変数の正規分布から多変数の正規分布に拡張する上でわかりやすく説明するための式変形です。

上記では、1変数の正規分布から、その積を用意して無理やり2変数にして、その式を式変換していき、分散共分散行列を含む形に変形してから、最後に独立性を外す形で説明しました。

変数変換トリック

ここまでで、多変数正規分布では、分散共分散行列が分布の形を決定していることを説明しました。

これは、例えば、「17歳の男性の身長、体重」のデータがあった場合に、身長の分散と体重の分散、そして身長・体重の共分散の3つの要素があれば、正規分布として分布を近似することができるということになります。

すごいですね。
大量のデータを、たった3つの要素で説明することができるということです。

それだけではありません。
多変数正規分布では、単一の分散の代わりに、分散共分散行列が使われています。

ということは変数変換トリック（Reparametrization Trick）が利用できるということになります。

変数変換トリックは一変数の場合は下記のように使えました。

$$z = \mu + \sigma \epsilon$$

ただし、

$$\epsilon \sim N(0,1)$$

この時、$z$は$N(\mu,\sigma^2)$からサンプリングされたデータ点であるとみなせるという手法です。

これを多変数に拡張すると下記のようになります。

$$z = \mu + \Sigma \epsilon$$

ただし、

$$\epsilon \sim N(0,I)$$

この時、$z$は$N(\mu,\Sigma)$からサンプリングされたデータ点であるとみなせます。

ここで、もし平均$\mu$の全ての要素が0の場合、

$$z = \Sigma \epsilon$$

と書くことができます。

正規分布において、平均を0にするという操作は、山の中心を原点に持ってくるように並行移動するという操作です。

これは、原点を各変数の平均であるとみなせば、並行移動前と同様に分析を行うことができるため、適切な条件を付与することで、同値な書き換えになります。

この時、$z$と$\epsilon$の間の分散共分散行列$\Sigma$は、変換行列として見なすことができるようになります。

つまり、標準正規分布からサンプリングされた点を、所望な分布からサンプリングされた点に変換することができる変換行列です。

こう考えると、分散共分散行列に分布の本質が入っているという考えも理解していただけるかなと思います。

固有値問題

では、

$$z = \Sigma \epsilon$$

において分散共分散行列$\Sigma$がどのような変換を司っているのかを、固有値問題を解くことで考えてみます。

ある変換行列に対して、固有値問題を解くということは、行列がその作用を受けるベクトル空間において、どのような変換を行うのかをより深く理解するための手段です。

ここでは、また簡単のために、具体的な分散共分散行列について解いてみます。

今回解く分散共分散行列は、

$$\Sigma = \begin{pmatrix} 6 & 2 \\ 2 & 3 \end{pmatrix}$$

です。

これは、変数$X$の分散は6、変数$Y$の分散が3、$X$と$Y$の共分散が2であるような、分散共分散行列になります。

固有値問題を解く

分散共分散行列$\Sigma$に対して固有値問題を解く場合、以下の固有値方程式を考えます。

$$\Sigma \mathbf{v} = \lambda \mathbf{v}$$

ここで
$\mathbf{v}$は固有ベクトル、
$\lambda$は固有値です。

上記の式は、変換行列$\Sigma$をある基底ベクトル$\mathbf{v}$に適用した時、基底ベクトル$\mathbf{v}$が定数倍されるような変換になる基底ベクトル$\mathbf{v}$を探すという問題です。

上記の式は、下記のように式変形できます。

$$\Sigma \mathbf{v} - \lambda \mathbf{v} = 0$$

$$(\Sigma - \lambda I) \mathbf{v} = 0$$

ここで、固有ベクトル$\mathbf{v}$がゼロベクトルの自明の例を除くと、上記の式が成立するためには下記が成立している必要があります。

$$\det(\Sigma - \lambda I) = 0$$

この式を「特性方程式」と呼びます。

書き方的に必要条件になっているように見えますが、これは必要十分条件であることがわかっています。
つまり、この行列式から得られた$\lambda$に対応する固有ベクトル$\mathbf{v}$は必ず存在することがわかっています。

重要なのは核の次元です。
核の次元とは、行列の核の持つ自由度やベクトルの数を表すものです。「列数-rank」で表されます。

具体的には、ある行列$A$に対して、次の線形方程式を考えます

$$A\mathbf{x}=0$$

この時、$\mathbf{x}$を行列の核と呼びます。

この時、$\det{A}=0$の時、Aの列数よりも必ずrankは小さくなります。
その場合、核$\mathbf{x}$の次元は必ず1以上になります。

その場合、

$$A\mathbf{x}=0$$

を満たす核$\mathbf{x}$において、自明なゼロベクトル以外のベクトルを含みます。

（これは、n個の解を求める際に、n-1個の連立方程式を利用していると考えるとわかりやすいです。その場合、何か一つの変数を固定すると、他の次元の解が固定されますが、その時に固有ベクトルが存在するように解を固定することができるということです。）

上記の前提をもとに今回の例を考えると

$$A = (\Sigma - \lambda I)$$

$$\mathbf{x} = \mathbf{v}$$

となります。

したがって、$A = (\Sigma - \lambda I)$を満たす$\lambda$が見つかれば、それに対応する核$\mathbf{v}$は必ずゼロベクトル以外のベクトルを一つ以上もつため、

$$\det(\Sigma - \lambda I) = 0$$

を解いて得られる固有値$\lambda$から、

$$(\Sigma - \lambda I) \mathbf{v} = 0$$

を満たす、固有ベクトル$\mathbf{v}$が必ず存在します。

では、実際に具体的な値を入れて、固有値を求めます。

$$\Sigma = \begin{pmatrix} 6 & 2 \\ 2 & 3 \end{pmatrix}$$

であるため、特性方程式は下記のようになります。

$$\Sigma - \lambda I = \begin{pmatrix} 6 - \lambda & 2 \\ 2 & 3 - \lambda \end{pmatrix}$$

行列式を計算して

$$\det(\Sigma - \lambda I) = (6 - \lambda)(3 - \lambda) - (2)(2)$$

$$\det(\Sigma - \lambda I) = (6 - \lambda)(3 - \lambda) - 4 \\ = 18 - 6\lambda - 3\lambda + \lambda^2 - 4 \\ = \lambda^2 - 9\lambda + 14$$

したがって、下記の二次方程式をときます。

$$\lambda^2 - 9\lambda + 14 = 0$$

解の公式より

$$\lambda = \frac{-(-9) \pm \sqrt{(-9)^2 - 4(1)(14)}}{2(1)} \\ = \frac{9 \pm \sqrt{81 - 56}}{2} \\ = \frac{9 \pm \sqrt{25}}{2} \\ = \frac{9 \pm 5}{2}$$

したがって、固有値は下記になります。

$$\lambda = 7,2$$

この固有値に対応する固有ベクトルを求めます。

$$(\Sigma - 7I)\boldsymbol{v_1} = \begin{pmatrix} 6 - 7 & 2 \\ 2 & 3 - 7 \end{pmatrix} \begin{pmatrix} v_{11} \\ v_{12} \end{pmatrix} = \begin{pmatrix} -1 & 2 \\ 2 & -4 \end{pmatrix} \begin{pmatrix} v_{11} \\ v_{12} \end{pmatrix} =0$$

$$(\Sigma - 2I)\boldsymbol{v_2} = \begin{pmatrix} 6 - 2 & 2 \\ 2 & 3 - 2 \end{pmatrix} \begin{pmatrix} v_{21} \\ v_{22} \end{pmatrix} = \begin{pmatrix} 4 & 2 \\ 2 & 1 \end{pmatrix} \begin{pmatrix} v_{21} \\ v_{22} \end{pmatrix} =0$$

これらを解くと固有ベクトルは

固有値が7のとき

$$\boldsymbol{v_1} = \begin{pmatrix} \frac{2}{\sqrt{5}} \\ \frac{1}{\sqrt{5}} \end{pmatrix}$$

固有値が2のとき

$$\boldsymbol{v_2} = \begin{pmatrix} \frac{-1}{\sqrt{5}} \\ \frac{2}{\sqrt{5}} \end{pmatrix}$$

と計算できます。

固有値問題の解釈

ここで得られた結果を解釈します。

分散共分散行列$\Sigma$の固有値問題を解いて、得られた結果は下記です。

固有値が7のとき

$$\boldsymbol{v_1} = \begin{pmatrix} \frac{2}{\sqrt{5}} \\ \frac{1}{\sqrt{5}} \end{pmatrix}$$

固有値が2のとき

$$\boldsymbol{v_2} = \begin{pmatrix} \frac{-1}{\sqrt{5}} \\ \frac{2}{\sqrt{5}} \end{pmatrix}$$

すなわち、

$\boldsymbol{v_1}$や$\boldsymbol{v_2}$を基底ベクトルとする軸上の点に対しては、変換行列を適用しても、定数倍でしか変化しないということです。

もっというと、データが最もばらつく方向が、このベクトルの方向になります。
（それ以外のベクトルにおいては、固有ベクトルの線形和の方向に変換されるため）

つまり、独立な正規分布の分散が最大になる方向がx軸やy軸といった基底ベクトル方向であるように、分散共分散行列を持つ正規分布の分散が最大になる方向は、固有ベクトルで表される基底ベクトル方向になります。

変換の可視化

ここまでの議論をわかりやすくするために、変換を可視化してみます。
変換元は、標準正規分布（平均0、分散$I$）からサンプリングされた点$\epsilon$です。

変換行列は、

$$\Sigma = \begin{pmatrix} 6 & 2 \\ 2 & 3 \end{pmatrix}$$

を利用します。

上記の変換行列（分散共分散行列）は、前の章で固有値問題を解いて、固有ベクトルを算出しています。
固有ベクトルは下記です。

$$\boldsymbol{v_1} = \begin{pmatrix} \frac{2}{\sqrt{5}} \\ \frac{1}{\sqrt{5}} \end{pmatrix}$$

$$\boldsymbol{v_2} = \begin{pmatrix} \frac{-1}{\sqrt{5}} \\ \frac{2}{\sqrt{5}} \end{pmatrix}$$

この固有ベクトルの向きをオレンジの矢印で表しながら、下記の変換式を可視化します。

$$z = \Sigma \epsilon$$

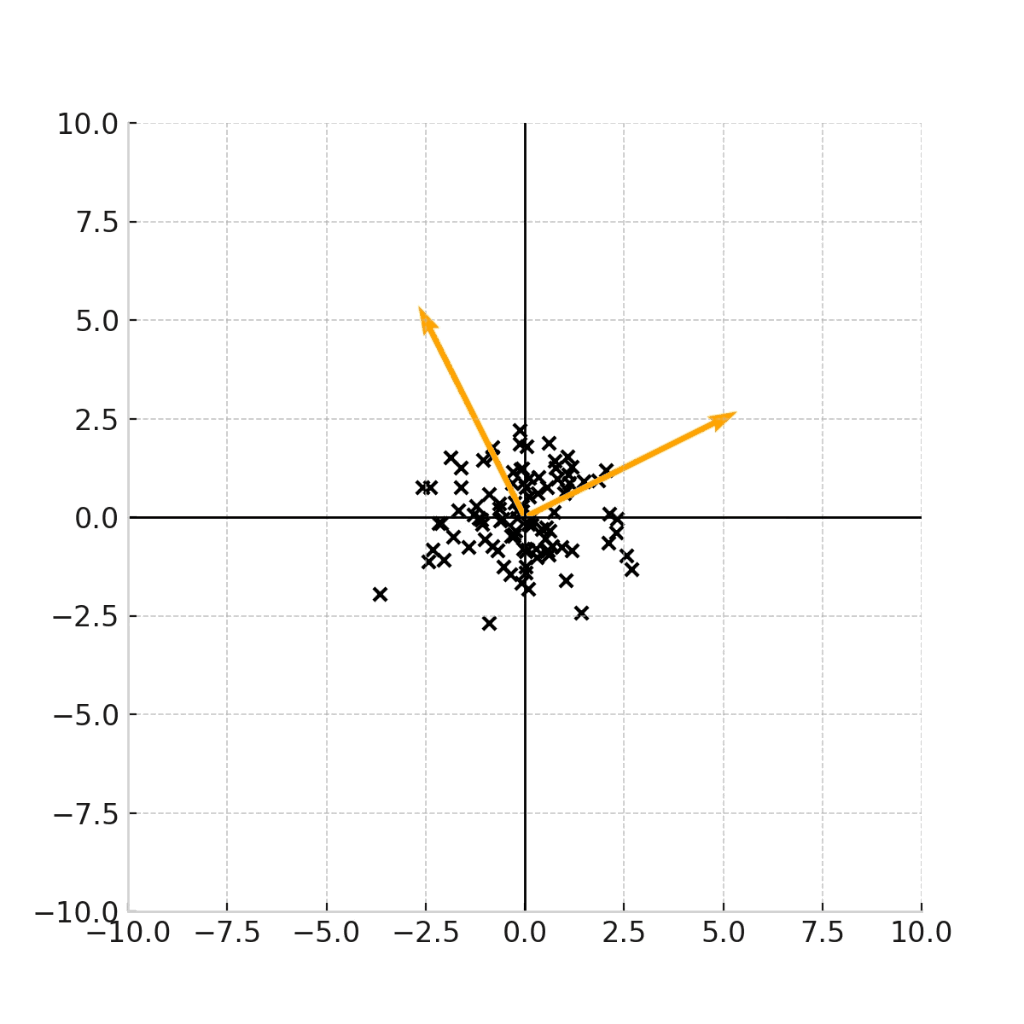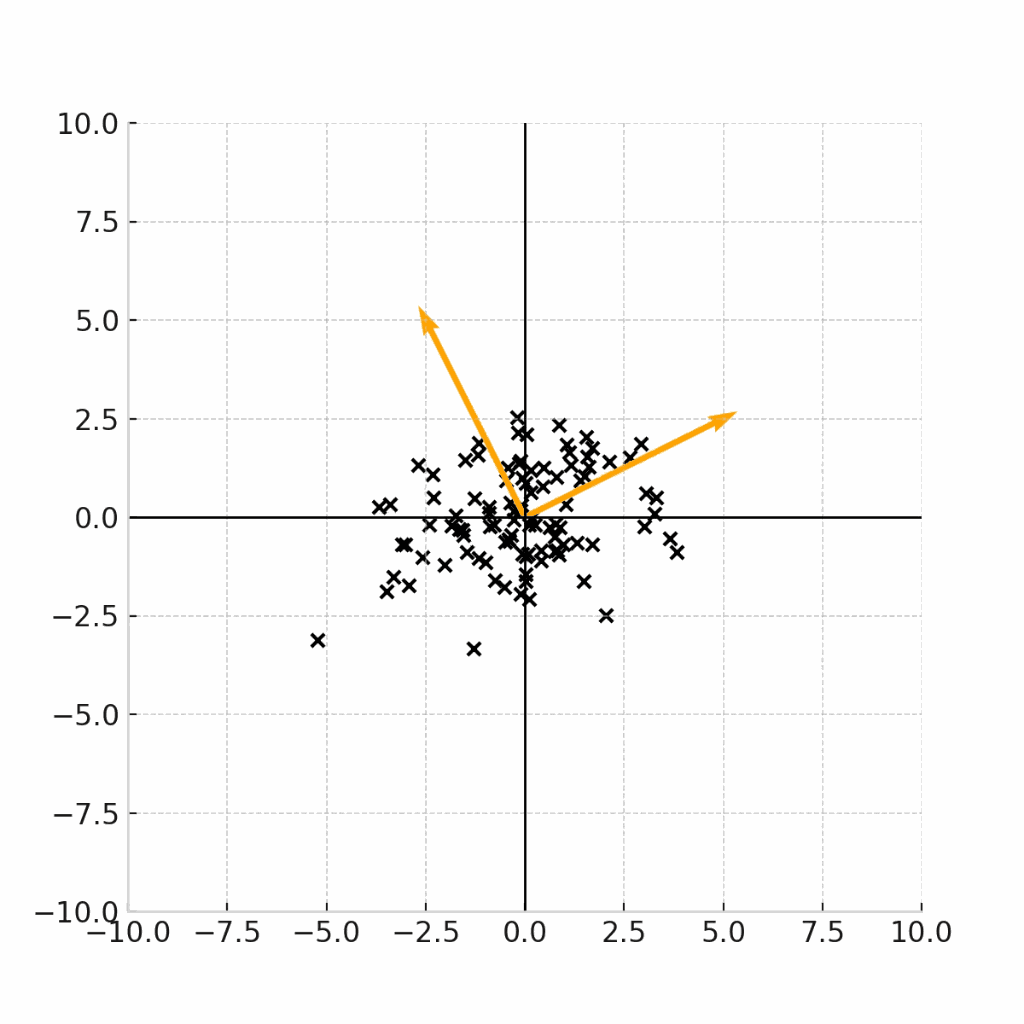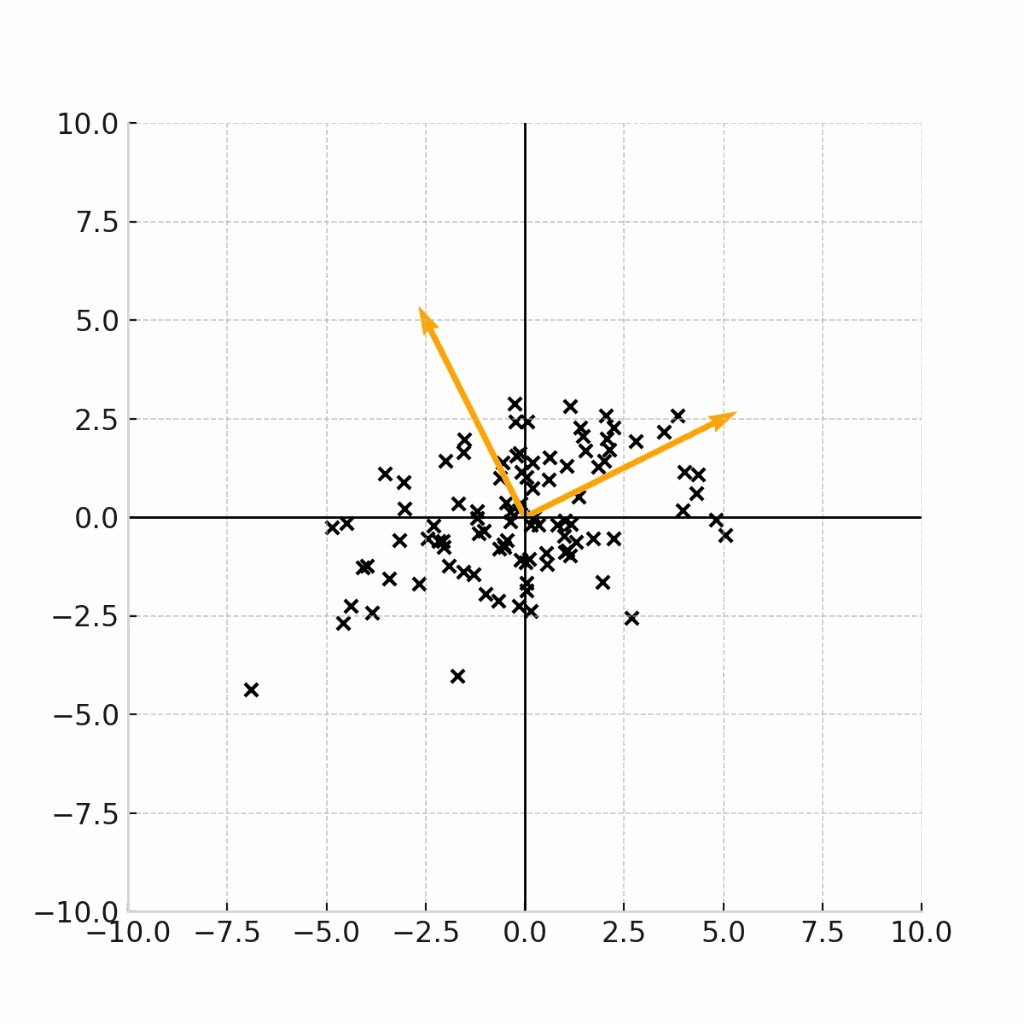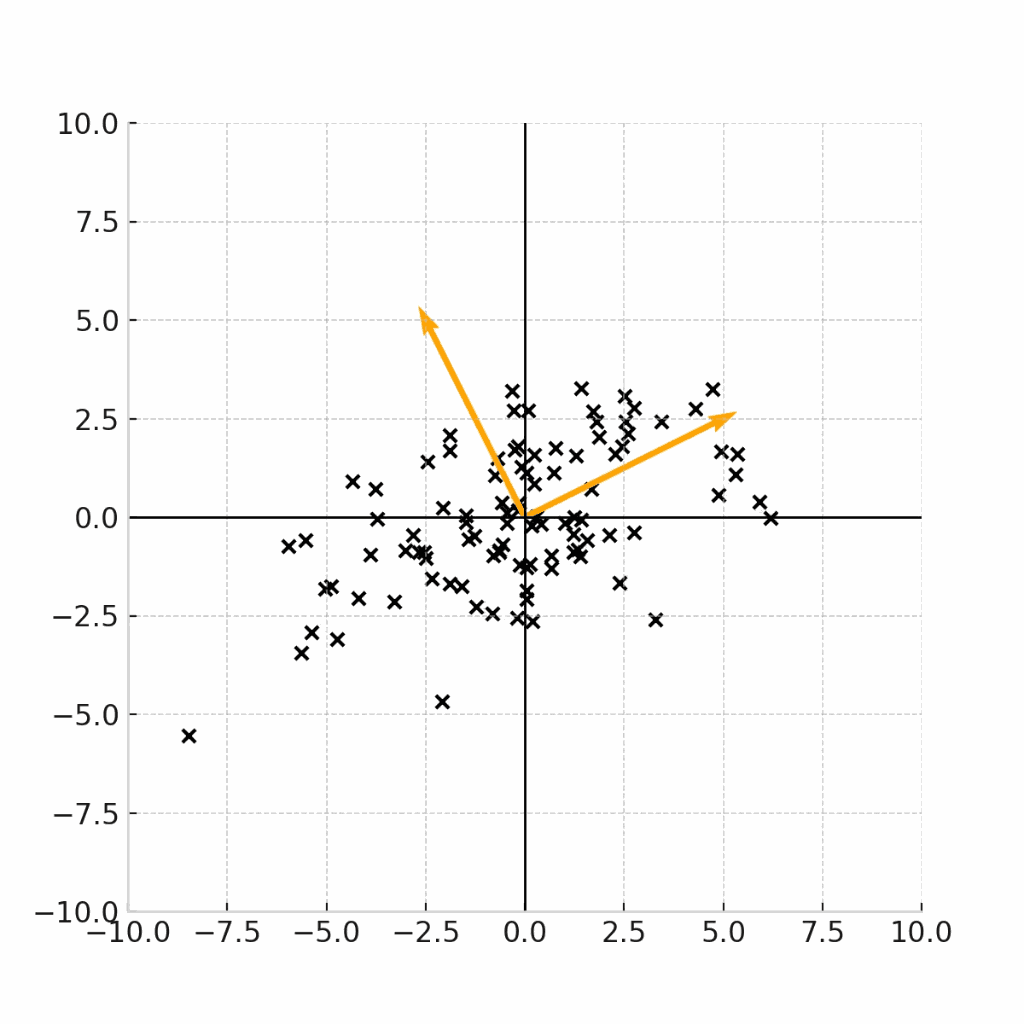
こちらの図から、実際に固有ベクトルの方向に分散が最大化するように、データサンプルが変換されていることがわかります。

主成分分析（PCA）

分散共分散行列に対して、固有値問題を解き、固有ベクトルを計算し、主成分により次元を削減する手法を主成分分析（PCA）といいます。

実は、前章まで実施してきたことは主成分分析です。
主成分分析を行うことで、ある変換行列において、変換後に方向を変えずに定数倍にスケールされるベクトル空間を求めることができます。

その性質を利用して、データに含まれる変動を効率よく説明できる新しい軸を見つけることができます。

実際に、上の動画を見て分かるように、変換後の分布の分散を最大化する方向が固有ベクトルとなっているため、あとは、（固有値が高い）固有ベクトルを基底ベクトルとする、新しい軸を用意して、1次元に投射すれば、データを1次元に圧縮して説明できるようになります。

高次元のデータは、低次元に圧縮することで、可視化したり分析しやすくなります。

（追記）
主成分分析に関係する続編書きました！
https://zenn.dev/asap/articles/ff8f34d19ca6a4

まとめ

分散共分散行列について思いのまま殴り書きしてみました。
分散共分散行列が分布の性質を反映しており、主成分分析といった非常に重要な分析手法に使われていることからも分かるように、非常に重要な量であることがわかると思います。

ここまで読んでくださってありがとうございました。

（おまけ）正規分布について補足

ここからはおまけです。
改めて、正規分布について改めて解説します。

まずは、1変数の正規分布について解説し、その後、分散共分散行列を利用する2変数の正規分布について解説します。

1変数正規分布

まず、ここでは、17歳の男性の身長のデータを無数に所持していると考えます。
私たちがしたいことは、これらのデータから、その特徴を分析することです。

分析をする上で、一つの良い可視化の方法はヒストグラムを作ることです。
ヒストグラムというのは、データをいくつかの範囲（ビン）に分け、その範囲ごとのデータの数を棒グラフのように表したものです。
横軸はデータの範囲、縦軸はその範囲に属するデータの数を示します。これによって、データがどの範囲に集中しているか、どの範囲に少ないかが視覚的に分かりやすくなります。

例えば、17歳の男性の身長のデータを無数に取得し、それをヒストグラムにした際、おおよそ平均身長付近の身長である人数が最も多く、そこから離れるにつれて、だんだん人数が減っていき、極端に身長が高い人などは、人数が少なくなるようなグラフを書くことが期待できます。

このような、平均付近にデータ点が多く存在し、平均から離れるほどに、データ点が少なくなっていくようなデータの分布は、正規分布という分布で近似することができます。

正規分布に近似することで、17歳の男性の身長のデータの出現確率を式で表現することができるようになります。
式で表現することで、バラバラだったデータ点を結びつけ、その特徴を大域的に理解することができるようになり、データ分析の効率を高めます。

注意

わかりやすさのために厳密性を捨てた説明をしています。
今回では、ヒストグラムを正規分布で、直接、近似することはできません。
あくまで正規分布は確率密度関数として利用することを前提としていますが、ヒストグラムは、ある特定のビンの範囲でのデータ量が縦軸になるからです。

しかしながら、データ量と確率には強い関係性があるため、ヒストグラムの形が正規分布に近い形である場合は、そのデータが現れる確率密度分布を正規分布で近似することができます。

正規分布の形

正規分布とは、下記のような式で表される分布をいいます。

$$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)$$

ここで$\mu$は分布の平均、$\sigma^2$は分布の分散です。

上記の分布は図にすると下記のようなベルカーブを描く分布になり、山が一番高くなる横軸上の点の数値が平均$\mu$になります。

こちらの図のように、平均付近が最もデータ数が多く、離れるにつれてデータ数が少なくなっていることがわかります。

正規分布は確率密度分布

正規分布は、確率密度分布です。
確率密度分布というのは、確率分布の連続値版です。

確率分布とは

確率分布の場合は、離散的な事象に対して、それぞれどの確率で発生するのかを分布として表したものになります。

例えば、サイコロの出目の場合は、サイコロの出目の出現確率が同様に確からしい場合、全て1/6の確率で出ることが期待されます。それを分布として表現すると下記のようになります。

このように、全ての事象に対して、それが出る確率を表現したものが確率分布です。
また、確率であるため、全ての総和は1になります。

確率密度分布とは

確率分布は事象が離散的な場合、非常に心強い味方になりますが、事象が連続の場合は、途端にその確率の特徴を捉えることができなくなります。

例えば、コンピュータが0−6までの「実数」を出力することを考えます。

この時、出力結果がちょうど3になる確率はわかりますか？

サイコロの場合は1/6でした。
しかしながら、連続になるとその確率は0になります。
0−6までの範囲に「無限」に存在する実数から、ちょうど3が選ばれる確率は0です。
このちょうど3というのは

$$3.000000000000000000000000000000000000000 \cdots$$

ということです。

$$3.000000000000000000000000000000000000001$$

では、ダメということです。

つまり、すべての実数において、その出現確率は0になります。
その場合、確率分布を書いても、すべて0になってしまうため、分布から分析をすることができません。

極限

実際には$\infty$は計算できないので、極限という考え方を導入することになります。
今回の場合は、各実数の出現確率は0に限りなく近づくと考えます。

$\epsilon-N$論法で考えると、出現確率における発生誤差$\epsilon$は、どんな$\epsilon$を持ってきても、その$\epsilon$より出現確率を小さくできる、「実数全体の数」$N$が存在する、と書けます。

したがって、ここで確率密度分布というものを導入します。

確率密度分布では、ある範囲の確率を、面積として表現した分布になります。

面積として考えることで、例えば水色の部分は、コンピュータが出力する実数が2から3の間にある確率が1/6とわかります。
緑色の部分も同様にコンピュータが出力する実数が4から6の間にある確率が1/3とわかります。

このように、連続な事象に対して確率密度分布というのは、ある特定の値の確率を表現するのではなく、ある範囲の確率を表現する分布になります。

データから確率密度分布を正規分布で近似する

改めて、正規分布とは、下記のような式で表される分布をいいます。

$$f(x) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp\left(-\frac{(x - \mu)^2}{2\sigma^2}\right)$$

この分布の形を調整するパラメータは、平均$\mu$と分散$\sigma^2$です。この二つの値によって、分布の形が変わります。

平均を大きくすると、正規分布は形を保ったまま右に並行移動し、分散を大きくすると、分布の中心の位置を保ったまま、左右に分布が引き伸ばされるように変換されます。

この二つのパラメータをいじって、元のデータ点の出現確率を確率密度分布として、正規分布で近似します。

この時、平均と分散はあくまで統計量のため、得られたデータ点の平均と分散を計算すれば良いです。

平均の定義は下記の式になります。

$$\mu = \frac{1}{N} \sum_{i=1}^{N} x_i$$

ここで、$N$はデータの総数、$x_i$は$i$番目のデータ点です。

続いて分散の定義は下記の式になります。

$$\sigma^2 = \frac{1}{N} \sum_{i=1}^{N} (x_i - \mu)^2$$

平均

平均はわかりやすいと思います。すべてのデータ点の値（この場合だと身長）を足し合わせて、データ総数で割っているだけです。

分散

分散について見ていきます。
$(x_i - \mu)^2$は、各データ点が平均値から、どのくらい離れているかを表します。
平均からの差分は、正の差分と負の差分があるため、打ち消し合わないために二乗して同じ土俵で誤差を計算しています。

したがって、分散は、平均との2乗誤差の平均をとっています。
一言で言うと、データのばらつきを見ている指標になります。

確率密度分布を正規分布で近似すると言うこと

ここまでで、データ点から平均と分散が得られてため、正規分布の式に値を代入することで、確率密度分布を近似できました。

式として確率密度分布を近似したため、この分布からサンプリングすることで、データを増やすことができます。

近似なため、正確に正しい分布ではないですが、この近似精度が非常に高い（取得したデータに偏りがなく、真の分布が正規分布に非常に近い形をしている）場合は、この確率分布にしたがってサンプリングしたデータの分布は、取得したデータの分布とほぼ一致します。

リアルなデータと一致するデータをサンプリングできる確率密度分布が得られたと言うことは、元のデータの特徴を完全に式に埋め込めたといっても過言ではないでしょうか。

つまり、ここまでで、17歳の男性の身長は、平均値がどのくらいで、どのくらいのばらつきを持って日本中に分布しているのかと言うことがわかってしまうわけです。

まとめ2回目

以上です。
ここまで読んでくださってありがとうございます！