拡散モデルの理論について（拡散過程の条件付き確率・逆拡散過程のスケジューラ）

はじめに

今回は拡散モデルにおいて重要な役割を果たしている拡散過程のノイズ付与の条件付き確率や、逆拡散過程におけるスケジューラについて、自身の忘備録のため記載します。
拡散モデルの理論については別で記事も書いています。基本的にはこちらに記載している内容は理解している前提で記事を記載しています。
https://zenn.dev/asap/articles/4092ab60570b05

数式などほとんど使わずに、ふんわり理解できるように記載したため、問題なく理解できると思います。

今回は、前回の記事では触れられなかった、スケジューラの理論をゴールとして、その他の拡散モデルの理論で前回記事で触れていなかった内容を記載できればと思います。
（拡散モデル自体の説明は多いですが、スケジューラの理論まで触れている本や記事は少ないなと思っているので、参考になれば幸いです）

スケジューラの存在意義

前回の記事でも記載しましたが、拡散モデルは下記の微分方程式（逆拡散過程）を解くことで、自然画像$x$を取得します。

$$d\mathbf{x} = \left[\beta(t)\mathbf{x} + \alpha(t)\nabla_{\mathbf{x}} \log p(\mathbf{x})\right] dt$$

（今は、$\beta(t)$と$\alpha(t)$は適当です。あまり深く考えず時間によって変わる関数くらいに思っていてください）

しかしながら、拡散モデルのパイプラインでは、連続の微分方程式を解くことはできないため、離散的な処理に変更し、全体のステップ数を増やすことで、なるべく連続での処理に近くしています。

離散的な変更式は下記のようになります。

$$x_{t-1} = x_t + \beta(t)x_t + \alpha(t)\nabla_{x_t} \log p(x_t)$$

また、前提のステップ数は大体$T=1000$が使われます。
このステップ数を大きくすることで、常微分方程式の連続性を担保して、生成された画像が劣化することを防いでいます。
逆にいうと、このstep数が大きいと、微分方程式を数値的に解く際の誤差がどんどん大きくなってしまうため、画質が悪くなってしまいます。

すなわち、逆拡散過程において、1000回の推論を実施することによって、拡散モデルは画像を生成します・・・・・
1000回・・・・

はい、1000回なんて待てないですね。
そこで登場するのがスケジューラと呼ばれるものです。

スケジューラを利用することで、本来1000回の推論stepが必要なところを、50回や20回のstep数で劣化を抑えながら画像を生成することができます。

スケジューラの種類

Diffusersライブラリでは下記のようなスケジューラがよく使われます。

DPMSolverMultistepScheduler
EulerDiscreteScheduler
EulerAncestralDiscreteScheduler

などです。一番上のやつはDPM++ 2M Karrasという表記の方が馴染みが深いかもですね。

スケジューラによる処理の解説

今回はEulerDiscreteSchedulerに絞って解説していきます。（一番簡単なので）
このスケジューラは、常微分方程式を解く際に、一次近似により数値計算を行い、数値的にとく解法になります。オイラー法と呼ばれます。（Euler=オイラー）

したがってEulerDiscreteSchedulerとは、オイラー法を利用した離散的な微分方程式を解くスケジューラという意味です。

さらに、EulerDiscreteSchedulerは、各stepごとにおいて、その時点からわかる0step目のクリーン画像を直接推定して、出力することができる面白いスケジューラです。
（私の過去の記事において、生成途中を可視化している記事がありますが、それはこのスケジューラの0step目のクリーン画像を直接推定することができる機能を利用しています）

ではまず、スケジューラの処理を理解するにあたり、下記の流れで解説していきます。

• 拡散過程における、各stepごとのノイズ付与の詳細な式
• t step目のノイズ付与画像を0 step目のクリーン画像との関係性の整理
• 0 step目のクリーン画像の推定方法
• 常微分方程式を一時微分で解く

拡散過程におけるノイズ付与

1step間の条件付き確率の拡散過程

拡散過程におけるノイズ付与に関して振り返ります。
t-1 step目からt step目への拡散過程でのノイズを付与する条件付け確率は次の式で表現されます。
（上の式での $\alpha(t)$、$\beta(t)$とは全く関係ないことに注意してください）

$$q(\mathbf{x}_t | \mathbf{x}_{t-1}) = \mathcal{N}\left(\mathbf{x}_t; \sqrt{\alpha_t} \mathbf{x}_{t-1}, \beta_t I \right)$$

ただし、

$$\mathcal{N}\left(\epsilon; \mu, \sigma I \right)$$

は、平均$\mu$、共分散行列が$\sigma I$のガウス分布であり、

$$\beta_t = 1 - \alpha_t$$

$$0 \lt \beta_1 \lt \beta_2 \lt \cdot\cdot\cdot \lt \beta_T \lt 1$$

の関係があります。

ここで、$\alpha_t$のみの式で考えると下記の式になります。

$$q(\mathbf{x}_t | \mathbf{x}_{t-1}) = \mathcal{N}\left(\mathbf{x}_t; \sqrt{\alpha_t} \mathbf{x}_{t-1}, (1 - \alpha_t) I \right)$$

なぜ急にこんな式が出てくるのかというと、サンプリングとしてReparameterization Trickを利用して書き換えるとわかりやすいです。
上記のガウス分布からのサンプリングはReparameterization Trickにより、次の式で表せます。

$$\mathbf{x}_t = \sqrt{\alpha_t} \mathbf{x}_{t-1} + \sqrt{1 - \alpha_t} \epsilon$$

ただし、

$$\epsilon \sim \mathcal{N}(0, I)$$

となります。

ここで、$0<\sqrt{\alpha_t}<1$であるため、上記の式の解釈は、拡散過程において、t-1 step目のサンプル$\mathbf{x}_{t-1}$を$\sqrt{\alpha_t}$で減衰させて、定数倍したノイズ$\epsilon$を付与して、次のstepのサンプル$\mathbf{x}_{t}$を作成する式になります。

イメージは下記です。

このように、$q(\mathbf{x}_t | \mathbf{x}_{t-1})$を定義することにより、stepごとに少しずつサンプルの信号を減衰させて、だんだんとノイズだけが残るように拡散過程を定義することができます。

加えて、この式は、拡散過程における常微分方程式の離散版である下記の式と一致することがわかります。

$$\mathbf{x}_{t} = (1 - \beta(t))\mathbf{x}_{t-1} - \alpha(t)\nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t)$$

ただし

$$-\alpha(t)\nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t) = \sqrt{1 - \alpha_t} \epsilon$$

$$1-\beta(t) = \sqrt{\alpha_t}$$

です。

前回の記事において、$-\alpha(t)\nabla_{\mathbf{x}_t} \log p(\mathbf{x}_t)$は、サンプル$\mathbf{x}_t$において、自然画像の分布に対する対数尤度である$\log p(\mathbf{x}_t)$を小さくする向きへの更新に相当すると説明している通り、それが、拡散モデルではノイズ$\epsilon$の方向になるのは不思議ではありません。

初期stepからの条件付き確率の拡散過程

$$q(\mathbf{x}_t | \mathbf{x}_{t-1}) = \mathcal{N}\left(\mathbf{x}_t; \sqrt{\alpha_t} \mathbf{x}_{t-1}, \beta_t I \right)$$

前節で提示した上記の式はt step目のサンプルを生成するために、t-1 step目のサンプルを取得している必要があります。
これでは、画像1枚を学習するために、1000のサンプルを常に保持している必要があり、非効率です。
（もしくは、学習のイテレーションのたびに、k回の拡散過程（ノイズ付与）を繰り返して、k step目のサンプルを作成する必要がある）

そこで、$q(\mathbf{x}_t | \mathbf{x}_{0})$を導出することを目指します。
$q(\mathbf{x}_t | \mathbf{x}_{0})$が導出できれば、拡散モデルのネットワークにおいて、あるk step目を学習する際に、元のサンプルである$\mathbf{x}_{0}$から直接$\mathbf{x}_{k}$を導出することができるため、効率的です。

では、$q(\mathbf{x}_t | \mathbf{x}_{0})$を考えます。
ここで、拡散モデルはマルコフ過程でモデル化されているため、次の状態は前回の状態によってのみ確定します。（すなわち、前々回の情報は今回の情報には影響を及ぼさない）
したがって、最終的な時刻$t$における状態$\mathbf{x}_t$は、初期状態$\mathbf{x}_{0}$から時刻$t$までの全ての過程の積み重ねにより決定されます。

このプロセスを数式で表すと、次のように各時刻の条件付け確率を掛け合わせたものとして表現されます。

$$q(\mathbf{x}_t \mid \mathbf{x}_0) = \int q(\mathbf{x}_t \mid \mathbf{x}_{t-1}) q(\mathbf{x}_{t-1} \mid \mathbf{x}_{t-2}) \dots q(\mathbf{x}_1 \mid \mathbf{x}_0) d\mathbf{x}_{1:t-1}$$

上記の式は、すべての中間状態$\mathbf{x}_1,\mathbf{x}_2,\cdots,\mathbf{x}_{t-1}$において、条件付き確率の重ね合わせを積分している式であり、ある特定のサンプル$\mathbf{x}_0$からスタートし、得られるすべての中間状態のすべての可能性を考慮した分布を得る式になります。

例えば、$q(\mathbf{x}_2 \mid \mathbf{x}_0) = \int q(\mathbf{x}_2 \mid \mathbf{x}_{1}) q(\mathbf{x}_{1} \mid \mathbf{x}_{0}) d\mathbf{x}_{1}$を考えると、下記のような図になります。

$q(\mathbf{x}_{1} \mid \mathbf{x}_{0})$と$q(\mathbf{x}_2 \mid \mathbf{x}_{1})$の重ね合わせに対して、$\mathbf{x}_{1}$がとりうるすべての範囲で$q(\mathbf{x}_2 \mid \mathbf{x}_{1}) q(\mathbf{x}_{1} \mid \mathbf{x}_{0})$を足し合わせることにより、図の下半分のような分布を得ることができます。

これを、繰り返すことで、すべての$t$において、$q(\mathbf{x}_t \mid \mathbf{x}_0)$を得ることができます。

上記の図はわかりやすさのために、各山の中心を中間状態のサンプリング点に設定していますが、正確な条件付き確率分布は、

$$q(\mathbf{x}_t | \mathbf{x}_{t-1}) = \mathcal{N}\left(\mathbf{x}_t; \sqrt{\alpha_t} \mathbf{x}_{t-1}, \beta_t I \right)$$

であるため、山の中心はサンプリング点よりも原点に$\sqrt{\alpha_t}$移動した点であり、最終的に、原点が山の中心になるようなガウス分布になります。

上記の式からわかることとして、$q(\mathbf{x}_t \mid \mathbf{x}_{t-1})$がガウス分布として表現されることから、その重ね合わせ（すなわち中間状態による分布の足し算）の結果もまたガウス分布となるため、$q(\mathbf{x}_t \mid \mathbf{x}_0)$もまた、ガウス分布になることがわかります。

さて、ではどのようなガウス分布になるかを数式から導くため、下記の再帰的な式を考えます。

$$\mathbf{x}_t = \sqrt{\alpha_t} \mathbf{x}_{t-1} + \sqrt{1 - \alpha_t} \epsilon$$

$$\mathbf{x}_{t-1} = \alpha_{t-1} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_{t-1}} \epsilon_{t-1}$$

これらはそれぞれ、$q(\mathbf{x}_t \mid \mathbf{x}_{t-1})$と$q(\mathbf{x}_{t-1} \mid \mathbf{x}_{t-2})$のガウス分布の性質から、Reparameterization Trickにより得られます。

この2式をまとめると下記のようになります。

$$\mathbf{x}_t = \alpha_t \alpha_{t-1} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_{t-1}} \sqrt{\alpha_t} \epsilon_{t-1} + \sqrt{1 - \alpha_t} \epsilon_t$$

ここで、Reparameterization Trickの逆を考えます。

$$\mathbf{x}_t= \{\alpha_t \alpha_{t-1} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_{t-1}} \sqrt{\alpha_t} \epsilon_{t-1}\} + \{\sqrt{1 - \alpha_t} \epsilon_t\}$$

上記を考えると、$\epsilon_{t-1}$と$\epsilon_{t}$はともに、$\mathcal{N}\left(0,I\right)$からサンプリングされたノイズであるため、左のカッコは$\mathcal{N}\left(\alpha_t \alpha_{t-1} \mathbf{x}_{t-2}, (1 - \alpha_{t-1})\alpha_tI \right)$からサンプリングされたデータであり、右のカッコは$\mathcal{N}\left(0, (1 - \alpha_{t})I \right)$からサンプリングされたデータであるとみなすことができます。

その場合、2つのガウス分布からサンプリングされたデータの和は、二つのガウス分布の平均と分散の和をもつ、別の1つのガウス分布からサンプリングされたデータとしてみなすことができるため、下記が成立します。

$$q(\mathbf{x}_t | \mathbf{x}_{t-2}) = \mathcal{N}\left(\alpha_t \alpha_{t-1} \mathbf{x}_{t-2} + 0, (1 - \alpha_{t-1})\alpha_tI + (1 - \alpha_{t-1})I \right)$$

$$q(\mathbf{x}_t | \mathbf{x}_{t-2}) = \mathcal{N}\left(\alpha_t \alpha_{t-1} \mathbf{x}_{t-2}, (\alpha_t - \alpha_t\alpha_{t-1} + 1 - \alpha_{t-1})I \right)$$

$$q(\mathbf{x}_t | \mathbf{x}_{t-2}) = \mathcal{N}\left(\alpha_t \alpha_{t-1} \mathbf{x}_{t-2}, (1 - \alpha_t\alpha_{t-1})I \right)$$

さらに、Reparameterization Trickを適用させると、

$$\mathbf{x}_t= \alpha_t \alpha_{t-1} \mathbf{x}_{t-2} + \sqrt{1 - \alpha_t\alpha_{t-1}}\epsilon$$

となり、$\mathbf{x}_t$と$\mathbf{x}_{t-2}$の関係式を取得できます。
同様の流れを、$\mathbf{x}_{t-3}, \mathbf{x}_{t-4}, \cdots, \mathbf{x}_{0}$と最後まで繰り返していくと、最終的に下記の式を導出できます。

$$q(\mathbf{x}_t | \mathbf{x}_0) = \mathcal{N}\left(\mathbf{x}_t; \sqrt{\bar{\alpha}_t} \mathbf{x}_0, (1 - \bar{\alpha}_t) I \right)$$

ただし、

$$\bar{\alpha}_t = \prod_{s=1}^{t} \alpha_s$$

です。

以上より、$q(\mathbf{x}_t | \mathbf{x}_0)$を表現することができたため、初期サンプル$\mathbf{x}_0$から$\mathbf{x}_t$を解析的に取得することができます。

具体的には、上記の式にReparameterization Trickを適用させた、下記の式より得られます。

$$\mathbf{x}_t = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\epsilon$$

0step目のクリーン画像の推定

$$\mathbf{x}_t = \sqrt{\bar{\alpha}_t}\mathbf{x}_0 + \sqrt{1-\bar{\alpha}_t}\epsilon$$

の式が導出できれば、$t$ step目時点から直接0step目を推定することは簡単です。
上記の式を下記の形に式変形します。

$$\mathbf{x}_0 = \frac{\mathbf{x}_t - \sqrt{1-\bar{\alpha}_t}\epsilon}{\sqrt{\bar{\alpha}_t}}$$

ここで、拡散モデルのネットワークの出力を$\mu_\theta(\mathbf{x}_t,t)$とすると、学習時は

$$\mu_\theta(\mathbf{x}_t,t)=\epsilon$$

となるように学習しているため、十分収束後のモデル出力$\mu_\theta(\mathbf{x}_t,t)$は$\epsilon$に十分近づいていることが期待されるため、下記のように書き換えることができる。

$$\mathbf{x}_0 = \frac{\mathbf{x}_t - \sqrt{1-\bar{\alpha}_t}\mu_\theta(\mathbf{x}_t,t)}{\sqrt{\bar{\alpha}_t}}$$

モデル出力

学習時に

$$\mu_\theta(\mathbf{x}_t,t)=\epsilon$$

となるように学習していることは、実際のDiffusersの学習コードからも確認できる。

https://github.com/huggingface/diffusers/blob/main/examples/text_to_image/train_text_to_image.py

else:
    noisy_latents = noise_scheduler.add_noise(latents, noise, timesteps)

・・・

if noise_scheduler.config.prediction_type == "epsilon":
    target = noise

・・・

# Predict the noise residual and compute loss
model_pred = unet(noisy_latents, timesteps, encoder_hidden_states, return_dict=False)[0]

if args.snr_gamma is None:
    loss = F.mse_loss(model_pred.float(), target.float(), reduction="mean")

上記の通り、target = noiseと設定され、平均2乗誤差の最小化により学習されている。

上記の式から、ある$t$番目のstepのモデルの出力結果$\mu_\theta(\mathbf{x}_t,t)$と途中状態$\mathbf{x}_t$から、初期のクリーン画像$x_0$を算出できることがわかります。

この$x_0$は拡散モデルの各stepごとに出力できるため、これを並べることで、生成途中の可視化ができます。

生成途中の可視化の例

微分方程式をスケジューラとともに解く

ここまでで、拡散モデルの拡散過程でどのようにノイズを付与していくのかが理解できたと思います。
では、いよいよスケジューラがどのように拡散モデルの微分方程式を数値的に解いていくのかを考えていきます。

前回の記事では、横軸に$x$、縦軸に$P(x)$をとる確率密度グラフを利用して説明しましたが、今回は、横軸にstep数$t$、縦軸に$x$をとるグラフを利用して、その遷移を見ていきます。

上記の図は、$T$ stepかけて、サンプル$\mathbf{x}_t$が遷移している図になります。
左端は、逆拡散過程におけるスタート位置である、標準正規分布からサンプリングされた$\mathbf{x}_T$であり、右端は、自然画像$\mathbf{x}_0$であり、両端に記載されている分布は、それぞれのstepにおける確率密度分布を示しています。

青線は、サンプル$\mathbf{x}_t$が遷移する（理想的な）経路であり、モデルアウトプットの情報から、サンプル$\mathbf{x}_t$をうまくこの青線に乗せながら遷移させる必要があります。
青線からずれてしまうと、その分生成された画像の質が下がる方向に誤差として現れるため、より精度の高い方法で数値的に遷移経路を解く必要があります。

分散発散型拡散モデルで解く

これまでの解説で使っていた式は、
分散収束型の拡散モデルです。

分散収束型の拡散モデルでは、拡散課程は下記で定義されていました。

$$q(\mathbf{x}_t | \mathbf{x}_{t-1}) = \mathcal{N}\left(\mathbf{x}_t; \sqrt{\alpha_t} \mathbf{x}_{t-1}, \beta_t I \right)$$

しかし、この章では分散発散型の拡散モデルを考えます。
分散発散型の拡散モデルでは、下記の式で拡散過程が定義されます。

$$q(\mathbf{x}_t | \mathbf{x}_{t-1}) = \mathcal{N}\left(\mathbf{x}_t; \mathbf{x}_{t-1}, \sigma_t^2 - \sigma_{t-1}^2 \right)$$

そして、拡散モデルの場合、拡散過程において、分散収束型で学習していたとしても、分散発散型で推論しても結果が一致することが認められています。

従って、この章ではわかりやすいように分散発散型で考えます。
分散発散型で考えると、数値的に微分方程式を解く際に、図で説明がしやすいので図で説明します。

上記のように、一点の勾配を考えます。
前回の記事でも記載しましたが、ある点の勾配はモデルの出力が該当します。
すなわち、$\dfrac{d\mathbf{x}_t}{dt}$（1階の微分）の値は利用できます。

その上で、次のstepへの遷移は、図のように

$$\mathbf{x}_{t-1} = \mathbf{x}_{t} + \Delta T \dfrac{d\mathbf{x}_t}{dt}$$

とかくことができます。

学習時と同じだけのstepを利用して、逆拡散過程を解く場合は、

$$\Delta T = T/1000$$

となりますが、
オイラー法では、50stepほどで逆拡散過程を数値的に解くため、

$$\Delta T = T/50$$

となります。

もちろん、図で記載されているように、数値的に解いた点（赤色の円）と理想的な点（青色の円）との誤差はあります。
この誤差を小さくするために、（2階の微分を利用する）Heun法や（最大で4階の微分を利用する）ルンゲクッタ法で数値計算を近似することもできます。

もちろん、1階以上の微分値を得ることはできないので、Heun法やルンゲクッタ法では、元の式をテイラー展開し、その上で1階の微分値を複数の段階で取得することで、2階以上の微分値を近似して数値計算しています。
従って、1stepの計算に、複数回モデルの推論を繰り返す必要があるので、推論速度が遅くなってしまう課題があるため、拡散モデルではあまり使われません。

この問題に対しての解決策は正直わかっていませんが、拡散過程では微小なノイズを少しずつ自然画像に追加していくことで過程が定義されているため、実は、$x-t$グラフにおける遷移は非常になだらかであることが知られており、オイラー法でも十分な精度で近似できると言われています。

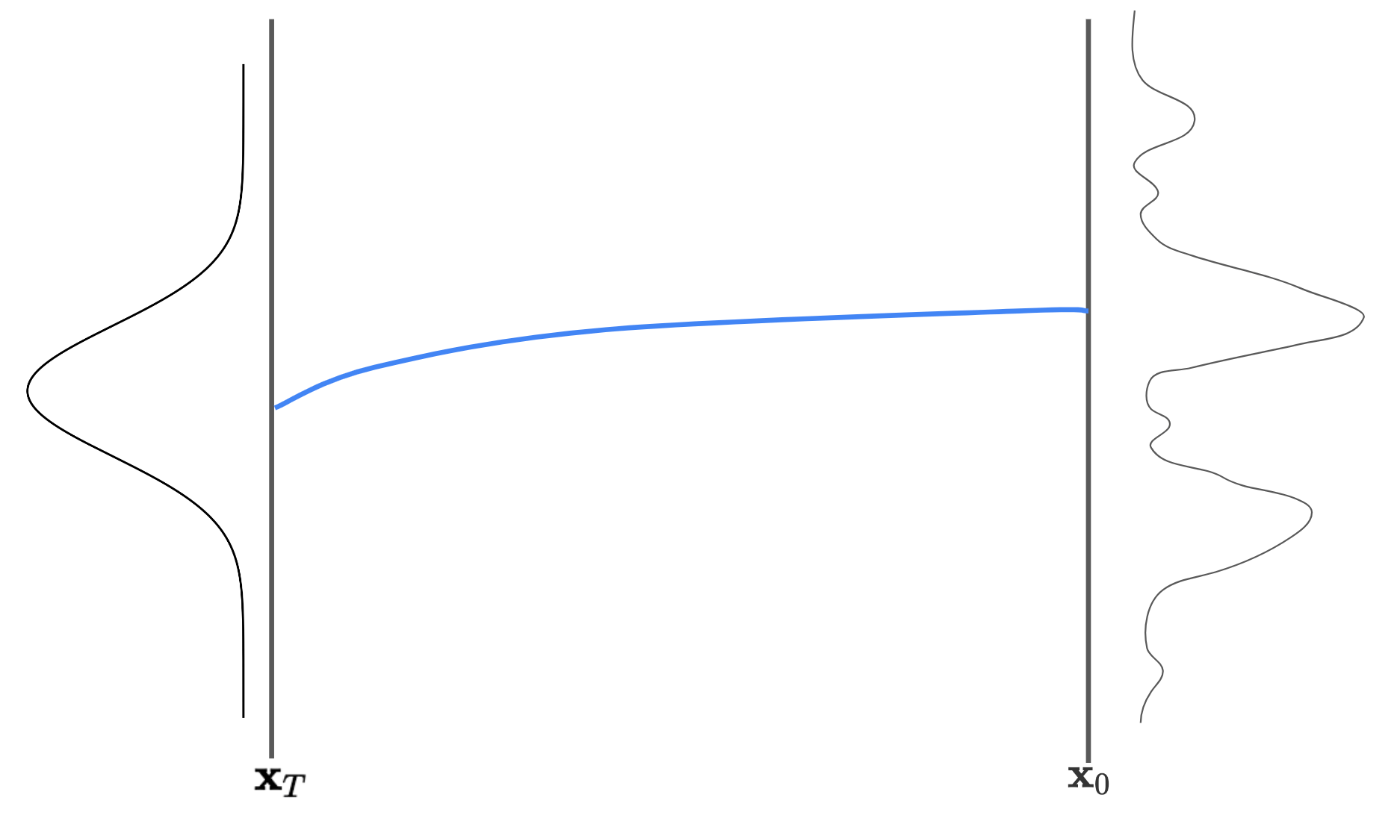
厳密ではないですが、上記のグラフのように、遷移がなだらかなため、オイラー法でも十分に近似が可能とのことです。

実際には

実は、上記の説明は厳密ではありません。
例えば、$\Delta T = T/50$とかきましたが、逆拡散課程において、ノイズが多い時は、大きくノイズを取り除いたほうがいいが、自然画像に近い時は、少しずつ慎重にノイズを取り除いたほうがいいため、そのように定義されることも多いです。

加えて、Diffusersライブラリという、拡散モデルを簡単にpythonスクリプトとして利用できるライブラリの中では、stepの移動量に$\Delta T$ではなく$\sigma_{t−1} - \sigma_t$を利用しています。

どうやら、timestep数である$t$ではなく、ノイズ量を司どる$\sigma$を利用するほうが性能が高くなるようです。

まとめ

今回は拡散モデルの理論について、特にスケジューラに関しての説明をしてみました。
皆様の役に立てると嬉しいです。

ここまで読んでくださって、ありがとうございました！